测量不确定度在汽车安全带安装固定点载荷试验中的研究与应用

袁自遥 吴 刚

(上海机动车检测认证技术研究中心有限公司，上海 201805)

0 前言

近年来，汽车工业的飞速发展给越来越多的汽车用户带来了出行和生活上的便利。车辆的安全性能逐渐成为用户的关注重点，尤其是车辆的被动安全性能。汽车安全带是汽车被动安全控制领域的重要组成部分。根据我国交管部门的统计，在可能导致死亡的交通事故中，使用安全带可使乘员生还机率提高60%。因此，针对汽车车身及座椅结构，国家出台了强制性法规《汽车安全带安装固定点、ISOFIX固定点系统及上拉带固定点》(GB 14167—2013)进行约束。

GB 14167—2013法规要求在规定的时间内，按时域曲线不间断地加载规定的载荷，安全带安装固定点在施加载荷和保持载荷过程中确保安全带功能不失效，固定点或周围区域允许有永久变形、产生裂纹或部分断裂。在试验期间，上下有效固定点均应满足相应要求(详见GB 14167—2013法规中4.3.2.5和4.3.3.6小节)[1]。

影响安全带固定点强度的因素很多。行业内对安全带安装固定点的研究主要集中在法规层面[3]、仿真或试验开发[4]及试验设备研制[5]等，加载载荷方面的研究较少。本文主要对试验和仿真过程中载荷的不确定性进行分析。在传统的安全带开发过程中，试验人员通常会采用法规中的载荷要求按照标准角度10°、最大角度15°，以及最小角度5°分别开展3次(甚至更多)仿真和试验。由于该试验内容是强制性检测项目，因此各企业为了通过检测，不可避免地在开发阶段针对此项目投入较多的仿真和试验资源。为了在开发过程中减少仿真和试验资源的占用，基于载荷的不确定度研究结果，本文提供仅使用一种单一载荷模式即可覆盖法规中所有载荷模式的方法，从而达到减少试验次数，节省试验时间，缩短车辆开发周期，提升被动安全性能开发效率的目标。

1 标准概述

1.1 法规要求

针对常用的三点固定汽车安全带，GB 14167—2013法规要求的载荷加载情况如图1所示。法规要求分别对人体上模块和人体下模块施加相应的外力，检测安全带固定点是否失效，并判断汽车安全带固定点是否安全可靠。

图1 安全带固定点加载示意图

法规具体加载要求为：沿试验载荷与水平方向的夹角α成向上(10±5)°施加载荷。先按总载荷的10%进行预加载，然后在60 s内缓慢加载至100%载荷；经过汽车安全带制造商的许可，也可在4 s内加载至100%载荷，且载荷至少要保持0.2 s[1]。人体上模块加载是通过模拟肩带施加的，其载荷大小与车辆类型相关。人体上模块施加相应试验载荷的要求为：M1类和N1类车辆(13 500±200) N；M2类和N2类车辆(6 750±200) N；M3类和N3车辆(4 500±200) N。同时，人体下模块施加相应试验载荷的要求为：M1类和N1类车辆(13 500±200) N；M2类和N2类车辆(6 750±200) N；M3类和N3车辆(4 500±200) N。

1.2 影响因素

影响汽车安全带安装固定点试验结果的因素较多，大致可分为输入、约束、结构3个方面。输入要素主要与载荷相关，如施加的载荷大小、方向、加载的时域曲线特征等；约束要素主要为车身的固定方式、安全带加载模块的阻尼设置等；而结构要素主要为座椅安装的连接结构、车身结构、安全带卷收器，以及安全带织带类型等。任何环节失效均可能导致座椅靠背失稳、椅腿变形过大、固定点撕裂、车身形变大、钣金塑变超标或螺栓断裂等失效现象，造成试验结果无效。所以，采用准确严苛的评估模式，覆盖全因素的影响，可达到减少频繁、重复试验的目的。

通过对上述因素的分析，并经过多个项目的规律总结，研究人员发现，在特定的结构要素下，输入要素是引起试验失效的最大原因，载荷的大小和方向是其中最重要的影响因素。因此，寻求一种高效的加载模式，使其可覆盖强制性检测时可能发生的最不利状态，从而提升试验和仿真的开发效率是非常有必要的。

2 载荷不确定度分析

2.1 载荷的数学模型

通过研究可知，载荷大小和方向是影响安全带固定点试验结果的重要因素之一。因此，在建立载荷数学模型时，研究人员需要全面考虑载荷的大小和方向。

如图1所示，根据GB 14167—2013法规要求，在试验过程中，人体上模块和人体下模块对安全带施加了相同的载荷，因此可使用载荷F代表人体上模块及人体下模块的载荷，可分解为水平方向的载荷Fx和垂直方向的载荷Fz2个分力。水平方向的分力Fx和垂直方向的分力Fz计算公式如下：

Fx=F·cosα

(1)

Fz=F·sinα

(2)

式中：F为试验载荷，单位N；α为试验载荷与水平方向的夹角， 单位(°)。

2.2 载荷分量的标准不确定度

不确定度是表征合理地赋予被测量之值的分散性，且与测量结果相联系的参数[2]。该参数可以是标准测量不确定度(标准偏差或其特定倍数)，或是给定包含概率的区间半宽度。不确定度通常由若干分量组成。由输入量的不确定度，可以计算得到输出量的不确定度。按不确定度理论分析，试验载荷F和试验载荷角度α相互独立，且为正态分布。水平方向载荷分力Fx的标准不确定度uc,Fx和垂直方向载荷分力Fz的标准不确定度uc,Fz计算公式如下：

(3)

(4)

式中：uF为试验载荷F的标准不确定度，单位N；uα为载荷角度α的标准不确定度，单位rad。

如表1所示，按照GB 14167—2013法规对M1类和N1类、M2类和N2类，以及M3类和N3类车辆的具体加载要求，可以分别计算出水平方向加载和垂直方向加载的各个不确定度的相关量。

表1 载荷分量的不确定度计算汇总

通过表1可进一步计算得到最大载荷及对应载荷角度，如表2所示。为了仿真和试验时操作方便，在实际测试的过程中，本文推荐载荷角度αs为15°，由此需要重新计算对应载荷。最后，在充分考虑可能的加载偏差和其他不利影响下，研究人员确定了便于操作的载荷值，如表3所示。

表2 不同类型车辆的加载载荷初始计算结果

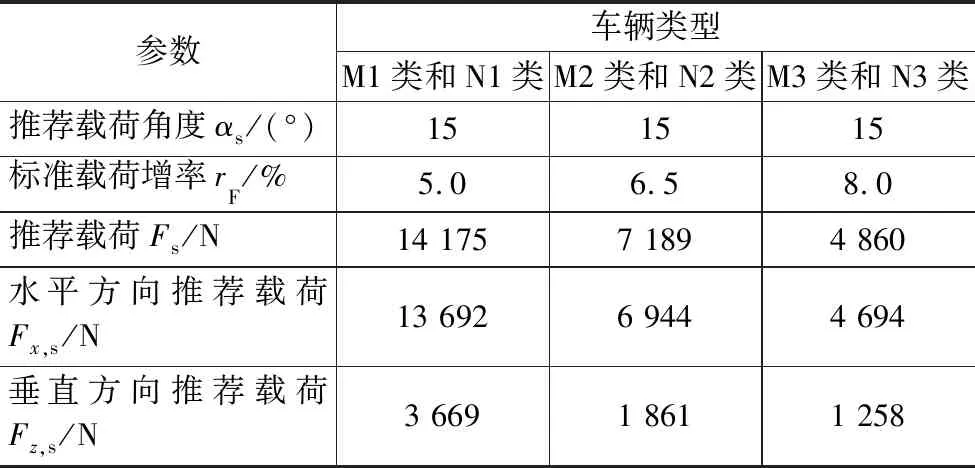
表3 推荐载荷值

3 结果分析

按GB 14167—2013法规规定，在载荷角度分别为5°、10°和15°时，传统试验方法中M1类和N1类、M2类和N2类，以及M3类和N3类车辆的标准载荷偏差时的分量计算如表4所示。

对比表3和表4中的数值，可以明显看出，若使用推荐的载荷，则可以完全覆盖GB 14167—2013法规中规定的载荷。因此，在开发阶段若使用推荐的载荷Fs及角度αs进行单一模式的仿真和试验，即可满足GB 14167—2013法规中规定的所有载荷要求。

表4 标准载荷偏差时的分量计算

4 结论

本文采用不确定度理论对GB 14167—2013法规中的载荷模式进行了研究，计算了水平方向和垂直方向载荷的不确定度，通过分析得到如下结论。

(1)相比3种典型载荷模式，仅使用单一载荷模式对确定的车型进行仿真和试验，可覆盖GB 14167—2013法规中所有的加载情况，节省了仿真和试验约67%的成本，提升了开发效率。

(2)推荐载荷增率：M1类和N1类车辆为5.0%，M2类和N2类车辆为6.5%，M3类和N3类车辆为8.0%。研究推荐载荷角度为15°。