思维导图促进小学数学学习“可视化”策略

林雅梅

小学生的数学学习特点是以直觉形象思维为主，因此在抽象的数学学习中，他们往往需要借助直观的可视化载体辅助发展抽象思维。思维导图符合学生思维发展的需求，图文并茂，能通过关键的词、句，简约地概括知识，使知识的呈现更为直观形象、简约美观。融思维导图于小学数学学习中，为学生学习抽象的数学知识、提高思维逻辑能力，提供了可视化的思维支架。由此，在引导学生运用思维导图促进数学学习“可视化”时，要多关注所学知识的结构特征、概念内涵以及学生的思维脉络走向三个方面，促使学生的数学思维品质不断得到提升。

一、“可视化”地呈现知识结构

思维导图是一种帮助学生理解数学知识本质、锻炼学习技能的有效学习方法。绘制思維图必须要引导学生找准知识的核心点，促其进行深度思考、在思考中厘清知识结构，再把知识结构绘制成简约可视的思维图。通过这样一系列的“找—思—理—绘”的过程，知识相应地变得有序分明、条理清晰，不仅夯实了学生的学习技能，也能有效地深化其对知识的理解。

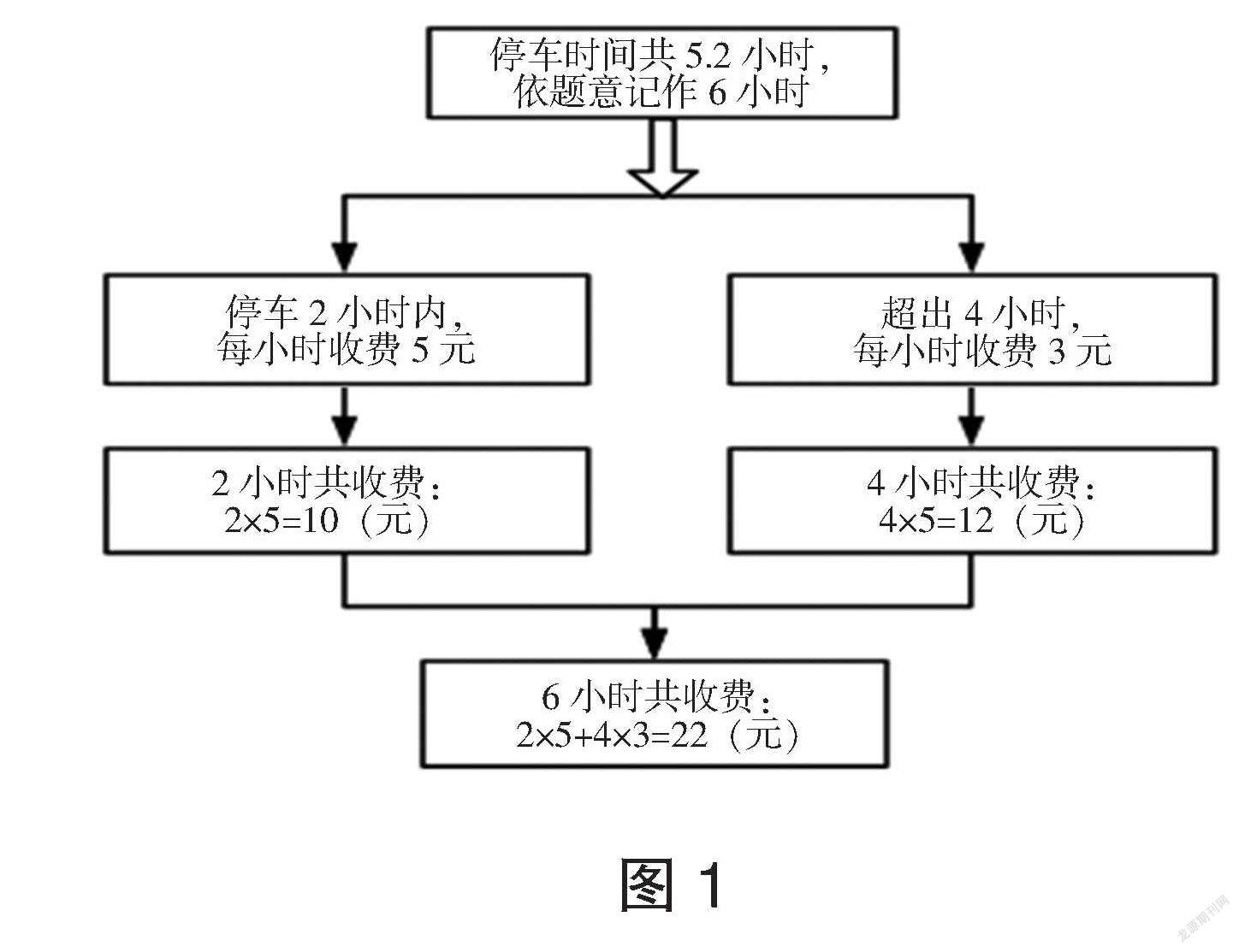
例如在教学五年级上册“分段计费问题”时，有这样一道题：“某地下停车场的收费标准是：停车两小时内，每小时收费5元，若超过2小时，则每小时收费3元（不足1小时的按1小时计算）。张叔叔停车5.2小时，他要付多少元的停车费？”解答的过程中，大部分学生出现了两种不同的错误列式情况，第一种，直接用5.2×5=26（元）;第二种，直接用5.2×3=15.6（元）。

仔细分析学生的错因，其实就是对“分段计费”的知识结构的理解不清晰，对关键点“为什么要分段”“如何分段”的理解思路混乱，他们只凭主观臆想做判断，却忽略了题目本身的有效条件——“若超过2小时，每小时收费3元（不足1小时的按1小时计算）”，以致缺少解题步骤，造成错误。鉴于此，笔者引导学生抓住题目的关键点“分段”来审清题意，并要求其依题目要求，按分段的方法绘制出本题的知识框架图（图1）。通过绘制可视化的思维图，促使学生对“分段算”的知识结构有了更清晰的理解，进而水到渠成地列出合理的算式，形成了对“分段算”知识的正确认知。

由上可知，教师适时地引导学生借助思维可视图对题目的知识结构进行辅助分析，能促使解题思路可视化、有序化，从而有效提升思维能力。

二、“可视化”地展现概念内涵

思维导图可帮助学生提升思维品质。学生根据题意绘制思维导图，能有效地在观察、比较、想象、思辨等高阶思维活动中，直观地发现、理解概念内涵，达到还原概念本质的目的，进而快速找到问题解决的策略。因此，课堂学习中，当学生出现概念模糊、思考滞塞时，可引导学生动手绘图，促使概念内隐的本质可视化，从而突破固有思维的限制，使思维驰骋于更广阔的空间。

例如在教学五年级下册“长方体和正方体表面积和体积”后，笔者出示了一道拓展题，辅助学生完善“立体图形表面积”的知识结构：“把2块棱长为15厘米的正方体木块拼成一个长方体。这个长方体的表面积是多少？”很多学生觉得很简单，认为只要先计算出一个正方体的表面积，再乘以2即可，由此列出了错误算式：15×15×6×2=2700（cm2）。

细究其错因，主要是学生对图形表面积这一概念的本质理解不到位，他们没有充分意识到相同的两个正方体拼合成一个长方体后，有两个相同的面重合了，使得原本能看得见的这两个表面，在拼合后消失了，与拼合前相比，这时的表面积就随之减少了两个面的面积，而这两个面的面积是不在表面积计算之列的。

于是，笔者引导学生根据题意来绘制思维可视图（图2），要求他们从中观察、思考并交流：拼合后的图形表面积有变化吗？增加了或减少了？为什么？如此一来，不仅有效降低了学生空间想象的难度，还促使他们形成了“图形拼合后”表面积变化的准确认知，在经历以上的“绘—察—思—说”学习过程中，最终得出了两种解决问题的正确方法：①152×6×2-152×2=2250（cm2）;②6×2-2=10（个），152×10=2250（cm2）。通过评价交流，学生认为第二种方法更为简洁方便。接着笔者又继续问：“把3块棱长为15厘米的正方体木块拼成一个长方体，这个长方体的表面积是多少？”学生借助刚才的思维图很快就举一反三地列出准确的算式，还以此递向推出：如果反过来把一个正方体切分一次，则会增加两个表面……通过自主绘图的“可视化”释疑学习活动，学生在思辨中正确建构了物体表面积概念，空间观念也得到发展，进而促进了思维品质的有效提升。

三、“可视化”地显现思维脉络

思维导图能把抽象、繁难、内涵丰富的知识变得形象、直观、美观、简约可视化，有效提升学习效率和质量。在课堂学习中自主小结这一环节，若让学生运用思维导图表达自己探究思考的过程和观点，可促其内隐的思维脉络得以“可视化”地显现，使课堂学习更形象、灵动和鲜活，从而极大地提升课堂学习的实效性，深度学习也就此悄然发生。

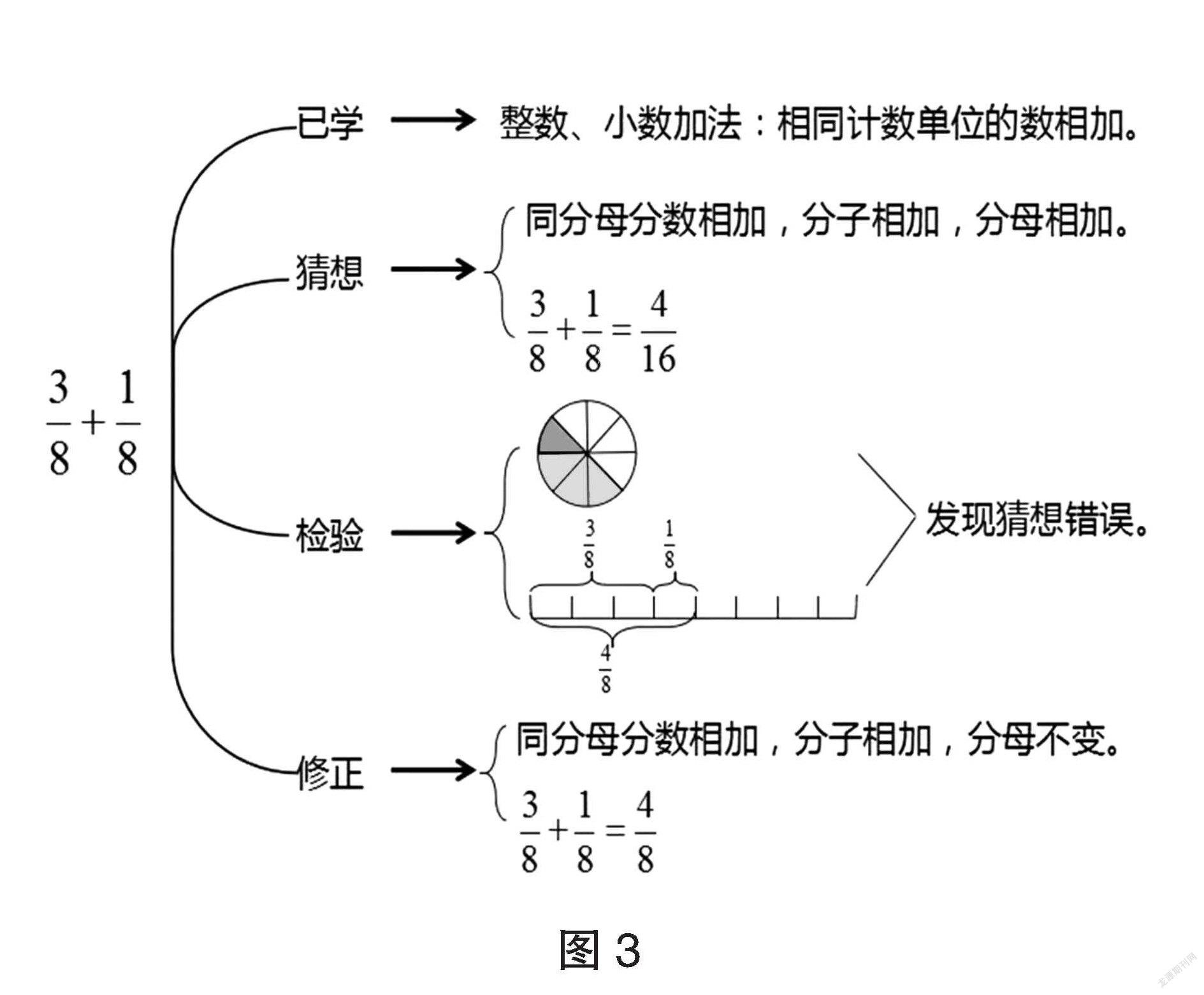
例如在教学五年级下册“同分母分数加法3/8+1/8”时，笔者先让学生以小组为单位讨论、猜测、推算同分母分数加减法的计算法则，再计算。学生充分交流后，基本形成了两种想法：一种是由整数加减法法则“把相同的计数单位的数相加”，推想出同分母分数相加时，也应该是分母加分母的和做新的分母、分子加分子的和做新的分子，即3/8+1/8=4/16;另一种则认为同分母分数相加时，分母不变、分子相加即可，所以3/8+1/8=4/8。究竟哪种算法正确呢？笔者就势引导学生进行检验，很快他们通过不同的画图方式发现：同分母分数相加时，相加的两个分数的分数单位没有变化，只是两次合起来的份数有变化，所以计算时，分母不变，分子相加即可，因此正确的计算式子应是：3/8+1/8=4/8。最后笔者要求学生把这一系列的思考检验过程绘制成思维导图呈现出来（图3）。

学生在以上自主绘图中，重现了猜想、实践、思辨等高品质的思维脉络，不仅深化了对新知本质的理解，掌握了同分母分数相加的计算方法，还增强了运用数形结合数学思想的意识，实现了有思想的深度学习。

综上所述，数学思维导图是链接思维和知识间的有效通道，是学生自主学习的脚手架，也是促进深度思维的利器。

注：本文系广东省教育技术中心2018年度教育信息化应用融合创新专项课题“可视化学习促进小学数学学科几何概念教学改革的实验研究”（项目编号：18JX07128）阶段性研究成果;佛山市教育科学“十四五”规划教育信息技术研究课题“小学数学可视化教学模式的实践探究”（课题编号：fset2021047）阶段性研究成果。