DINEOF重构遥感叶绿素a数据质量分析

刘超洋，魏永亮，2，3，邹斌

(1.上海海洋大学 海洋科学学院，上海 201306；2.上海河口海洋测绘工程技术研究中心，上海 201306；3.上海海洋大学 国际海洋研究中心，上海 201306；4.国家卫星海洋应用中心，北京 100081；5.南方海洋科学与工程广东省实验室(广州)，广州 511458)

0 引言

浮游植物对全球大气二氧化碳的波动和海洋系统的初级生产力有重要影响。对于海洋，叶绿素a(chlorophyll a，下称Chl-a)浓度是浮游植物细胞内现存量的一个通用指标，因为它普遍存在于所有浮游植物中，因此评估初级生产力时，可以将其通过同化系数联系起来，反映水域中浮游植物的光合作用能力[1]。Chl-a浓度分布受海洋环境因子影响，深入了解其变化有助于更好地理解海洋动力过程，如上升流、锋面和涡流，为环境监测、渔业资源分布、防灾减灾提供重要基础资料[2-3]。

基于可见光和近红外波段的海洋水色遥感技术可以实现全球海洋生态环境的大尺度、动态、连续监测，因此成为观测、反演Chl-a浓度的重要手段[4]。然而，水色遥感经常受到云、太阳耀斑、厚气溶胶和其他现象的影响，使得海洋水色遥感数据在时空维度上存在很多不足[5]。比如，中等分辨率成像光谱仪(moderate resolution imaging spectrometer，MODIS)的测量结果显示，在全球范围内，陆地上空的云占比约为55%，具有明显的季节循环，而海洋上空的云占比更高，约为72%，且季节变化不明显[6]，全球海洋上空无云条件下只有约50%的像素是高质量的[7]。传感器本身可能存在技术参数设置或故障问题，导致大面积数据缺失。此外，大气和传感器的影响也可能带来目标信号以外的噪声信息，使得提取有效的遥感信息变得困难。这些缺失数据严重影响了水色遥感的时空连续性和利用效率，缺失的数据也可能包含研究区域的重要信息[8]。

针对上述Chl-a遥感数据出现的问题，国内外学者已研究和发展了一系列插值方法，如地统计学插值法(geostatistical filling)[9]、最优插值法(optimal interpolation，OI)[10]、奇异谱分析法(singular spectrum analysis，SSA)[11]和数据插值经验正交函数法(data interpolating empirical orthogonal function，DINEOF)[12]。在这些方法中，DINEOF方法应用最为广泛，该方法是Beckers和Rixen共同提出的，基于EOF分解来重构缺失数据，并利用经验校正程序确定最佳模态数，无需参数且自适应。Alvera-Azcarate等[13]对这一方法引入Lanczos 算法，并将其正式命名为DINEOF，与最优插值法重建结果进行比较，两种方法得到的结果非常相似，但DINEOF计算时间缩短了近30倍。

DINEOF算法目前已广泛应用到卫星遥感数据重构，而研究重构数据质量的工作尚不多见。Alvera-Azcarate等选取缺失率为40%、60%和80%的数据集，采用DINEOF方法重建亚得里亚海海表温度数据，发现均方根误差(root mean square error，RMSE)随着数据缺失率增加而增加，但增幅较小。Sirjacobs等[14]重构中等分辨率成像光谱辐射计(medium resolution imaging spectrometer，MERIS)的总悬浮物和Chl-a浓度数据，通过交叉校正集的信噪比、测量相关系数以及重构前后数据的均方根误差对重构结果进行评价。王跃启等[15]对宽视场海洋观测传感器(sea viewing wide field of view sensor，SeaWiFS)和MODIS Chl-a数据分别单独重构和组合重构后的数值特征进行了比较分析，认为两种重构方法精度区别不大，但是组合方法能有效地重建完全缺失时段的数据。马翱慧等[16]对南海北部海域MODIS Chl-a数据进行重构，从时空特征、计算模型精度指标等对重构结果进行评价。郭海峡等[17]对SeaWiFS和MODIS台湾海峡Chl-a缺失数据重构，从重构前后数据的时空误差和时空变化等方面评价了重构数据的合理性。通过对重构数据的质量分析，马翱慧等和郭海峡等认为提高原始数据时空覆盖率可以降低因算法原理的局限性而导致的时空平滑。

以上研究表明，DINEOF方法取得了很好的重构效果，但DINEOF重构后，原始与重构数据相对误差的空间分布以及数据缺失率与相对误差、重构前后数据的相关性是否存在一定的关系均没有涉及。南海位于太平洋西部海域，纵跨热带与亚热带，是一个半封闭边缘海，每年11月到次年4月，全海域受东北季风控制，6到8月为是西南季风强盛期，属于典型的季风区[18-19]。此外，南海夏季和秋季云覆盖区域较多，可达80%，导致遥感数据缺失率很高，无法满足时空特征变化研究的需求[20]。基于上述考虑，本文采用DINEOF方法，对南海多传感器融合Chl-a数据进行重构，并结合统计学方法，对缺失数据重构的质量进行探讨，旨在探讨重构前后数据误差的空间分布以及提高数据时空覆盖率是否可以降低时空平滑，并从相对误差各阶段所占比例来探讨DINEOF重构数据的质量，为水色遥感数据长期重构应用及DINEOF方法的改进提供一些参考依据。

1 数据、研究区域和方法

1.1 数据和研究区域

选取南海(5°N～25°N，105°E～121°E)作为研究区域，如图1所示。2009—2020年Chl-a月平均数据来源于GlobColor数据库(http：//hermes.acri.fr/)，其是采用Maritorena等[21]建立的生物光学模型对SeaWiFS、MODIS、MERIS和可见光红外成像辐射仪(visible infrared imaging radiometer，VIIRS)等遥感数据融合成的，其中2009—2010年数据是MERIS、MODIS、SeaWiFS 3种传感器融合产品，2011年1月至2012年1月数据是MERIS和MODIS融合产品，2012年2—4月数据是MERIS、MODIS、VIIRS 3种传感器的融合产品，2012年5月至2020年12月数据是MODIS、VIIRS两种传感器的融合产品，空间分辨率为4 km×4 km。

图1 研究区域水深图

1.2 方法

DINEOF方法原理在前人研究中已有详细介绍，这里不再解释。本文用DINEOF方法重构数据时采用两种方式，一种是完全重构海洋所有数据点，称为整体重构方式，另一种仅重构海洋缺失的数据点，称为缺失点重构方式。由于Chl-a遥感数据具有非高斯分布特征，数值范围广，因此重构前需进行以10为底的对数变换[22]。循环重构数据过程中，稳定EOF最优模态个数所允许的最大迭代次数设定为300。1E-4定义为自动停止迭代次数的阈值，当连续缺失数据重构的均方根误差与现有数据标准偏差的比值低于1E-4，便可认为迭代完成收敛。为了检验最优模态个数的可靠性，在最优模态个数+3个额外模态后，将停止数据重构。

G为原始数据相对重构数据的缺失率，其中原始数据点的个数为N0，重构数据点的个数为N1，函数表达如式(1)所示。

(1)

均值偏差BIAS用于度量重构数据与原始数据的偏离程度，偏差越高表示匹配程度越差。RMSE用来衡量重构数据Ai与原始数据Bi之间的均方根误差。重构数据Ai与原始数据Bi的相关系数(correlation，CORR)表示二者相关关系密切程度。

2 结果与讨论

2.1 原始数据缺失率

2009—2020年144个月融合Chl-a遥感数据点总个数为19 604 160，其中缺失数据点总个数为1 868 399，整体缺失率占比9.53%。图2显示的是2009—2020年融合Chl-a数据缺失率统计情况。

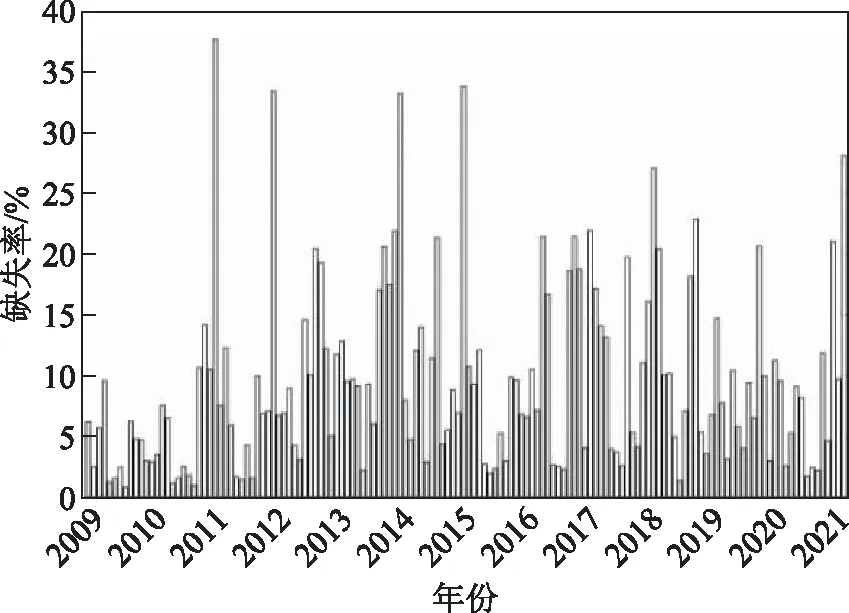
图2 2009—2020年各月缺失率

图2是各月缺失率柱状图。可以发现，数据缺失率较低的月份集中在5—9月，即春末至秋初季节，同时2009—2011年在此期间的缺失率整体低于此后9年同期数据。Chl-a浓度通过光学传感器观测反演获得，数据缺失率表明该区域上空云比较多。这说明2012年往后，南海5—9月份云量较之前3年同期均有增加，但具体原因需要深入探讨。

表1是2009—2020年融合Chl-a数据缺失率统计，缺失率区间在0～5%之间的占比最高，为33.33%，其他区间渐次降低，缺失率在20%以下的占比为88.19%，缺失率在30%以下占97.22%，基本覆盖所有月份。同单传感器Chl-a数据缺失率对比，多传感器融合Chl-a数据缺失率显著降低。

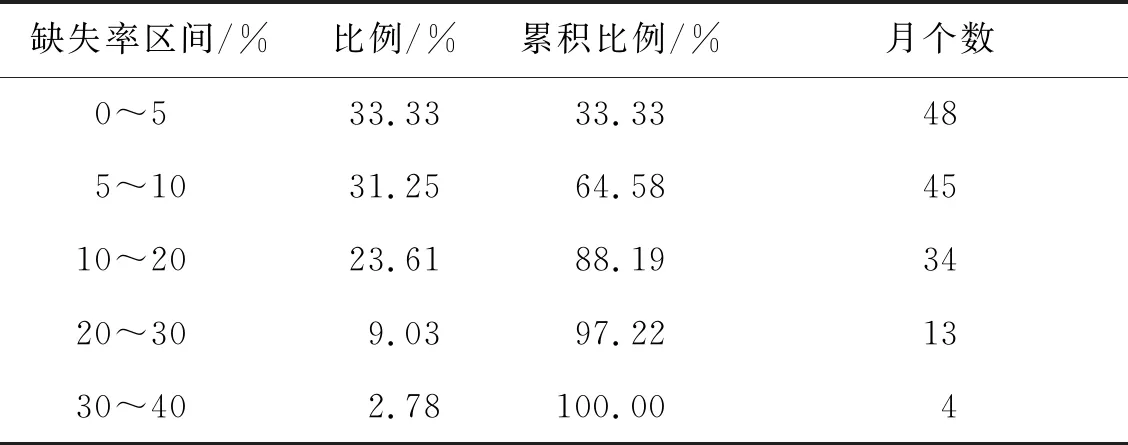
表1 2009—2020年融合Chl-a数据缺失率统计

2.2 重构模态数及重构数据质量分析

采用DINEOF重构Chl-a数据过程中发现，整体重构和仅缺失点重构两种方法保留的EOF最优模态数和各模态最优交叉验证次数完全相同。两种方法区别在于缺失点重构仅对缺失的数据进行，保留原始数据，而整体重构对所有数据重构，不保留原始数据。

图3是重构模态数和各模态交叉验证迭代次数。图3(a)显示，在交叉验证重构过程中RMSE随着EOF模态数的增加整体上呈现不断降低的趋势，直到完成迭代收敛，之后RMSE随着EOF模态数的增加整体上呈现不断升高的趋势，但变化不明显。黑色箭头表明在第14个EOF模态完成迭代收敛，对应的最优保留模态数和RMSE分别是14和0.145 9 mg·m-3。图3(b)是各模态交叉验证迭代的次数，与最优模态数下的RMSE相比，尽管额外3个模态的RMSE和第14模态RMSE差距很小，但交叉验证次数和时间急剧增加，并在第17模态达到重构限定的最大交叉验证次数300，说明前14个模态是DINEOF重构数据保留的最佳模态。

图3 重构模态数和各模态交叉验证迭代次数

在数据缺失位置上，为验证整体重构和缺失点重构得到的重构数据是否完全相同，将重构后缺失数据点分别提取后，计算CORR、RMSE和BIAS等统计数据。结果得出CORR为1，RMSE和BIAS均为0。图4为重构前后数据的质量分析。图4(a)显示，缺失数据匹配的数据点个数N为1 868 399，匹配数据点在对称线上分布，结合统计数据可知两种重构方法在缺失位置点的重构数据完全相同。

由于缺失点重构保留原始数据，对重构前后的数据质量分析没有意义，因此仅讨论整体重构数据的质量。图4(b)显示，原始数据与整体重构数据匹配的数据点个数N为17 735 761。从整体匹配的数据分析，Chl-a数据主要集中在-lg1.3～-lg0.5 mg·m-3的范围内，对应原始数据0.05～0.32 mg·m-3，此范围为南海中央海盆海域的Chl-a数据。低值-lg2～-lg1 mg·m-3即0.01～0.1 mg·m-3的范围内，整体重构的值大于原始值。高值0～lg1.5 mg·m-3即1～32 mg·m-3的范围内，为南海近岸海域的Chl-a数据，整体重构的值小于原始值。BIAS为-lg0.000 5 mg·m-3，RMSE为lg0.125 7 mg·m-3，CORR为0.93，与其他学者在不同海域研究结果相似且量级相同[23-25]。总体而言，原始数据与整体重构数据匹配的数据中除少数点外，均保持高度一致性，重构数据保留大部分原始数据的信息。

注：黑线是零偏置线，以10为底对数刻度的颜色条表示配对数据的密度分布。

2.3 原始与重构数据时空分布特征

为保证分析时空平滑现象时，排除Chl-a数据在相同海域不同月份变化过大造成的误差，选取缺失率分别为37.64%、20.43%、12.84%、2.58%的2011年、2018年、2013年、2020年的1月，研究不同缺失率原始数据与重构数据的Chl-a浓度时空分布，结果如图5所示。图5(a)至图5(d)是选取年份的原始数据分布，其特征为近岸叶绿素a浓度值较高而外海较低。图5(e)至图5(h)是缺失点重构后的Chl-a浓度分布，在缺失率较低的情况下，缺失点的重构数据分布与周围原始数据有较好的空间一致性，缺失率高的情况下，虽然在缺失点也有对应空间分布，但其准确性有待验证。

图5(i)至图5(l)是整体重构后的Chl-a浓度空间分布。可以看出，与相同时期的缺失点重构分布图相比，其空间分布更趋于平滑，很多细节被忽略。其原因是缺失点重构保留原始数据仅对数据缺失点进行重构，在数据缺失严重的海域平滑更明显，而整体重构对所有数据点进行重构，平滑体现在全海域，且缺失率越高的海域平滑越突出。通过分析2009—2020年144个月的Chl-a浓度分布，发现近岸海域多个月份存在数据缺失的现象，导致DINEOF重构时提取的重构模态信息不全，造成平滑加大，此外算法本身对缺失率较大的海域重构效果不佳，也会导致平滑加大。

图5 原始与重构数据时空分布

2.4 重构数据误差

上文提到，缺失率高的情况下，缺失点上重构的数据是否准确有待验证。为此，通过整体重构数据与原始数据的误差分析来判断重构数据质量，结果如图6所示。

图6 2009—2020年整体重构与原始数据相对误差各区间所占比例

二者相对误差在5%以下范围的占73.62%，10%以下范围占85.35%，20%以下范围占92.18%。在南海海域，除近岸海域外，冬季Chl-a的浓度一般在0.1～0.5 mg·m-3之间，其他季节更低。此外，盆地海域Chl-a的浓度也较低，一般小于0.1 mg·m-3。因此，从整体相对误差数据分析，本文设定相对误差范围在20%以内的重构数据具备可信度。

为分析重构数据在区域上的质量差异，仍以上述4个年份的1月份数据为例，研究不同缺失率整体重构数据与原始数据的绝对误差和相对误差的空间分布，结果如图7所示。从图7(a)至图7(d)可以清晰地看到绝对误差的正负值分布区域细节特征，在南海北部以及近岸区域正负误差较大，南海中南部误差相对较小。具体来说，大部分广东、北部湾、吕宋岛西北、越南东部等沿岸海域绝对误差为负值，说明在这些海域的整体重构值比原始数值小。越南湄公河东南海域和海南岛环岛沿岸海域误绝对误差大部分为正，说明在这些区域的重构值比原始数值大。出现两种不同结果的原因如前所述，是由近岸海域的数据缺失问题造成的。值得注意的是，图7(d)中部(16°N)有一个绝对误差负值条带区，仔细比较图5(h)和图5(l)会发现，图5(l)的整体重构结果对已有的原始数据的平滑更加明显，导致细节丢失且重构值变小。这意味着整体重构方式可能会导致原始数据质量发生变化。

图7 误差空间分布图

考虑到原始Chl-a浓度值差异较大，绝对误差只能判断重构数据与原始数据的大小关系，不能完全表示重构数据的质量高低。比如对于10 mg·m-3和0.1 mg·m-3的两个数据而言，相同的绝对误差0.1 mg·m-3所代表的重构数据质量完全不同。因此，在绝对误差的基础上，采用相对误差来进一步研究重构数据的质量。图7(e)至图7(h)是4个年份的相对误差分布图，可以看出相对误差大部分在20%以下，且相对误差高值并没有大面积出现，在南海近岸和远海都仅有零星分布，说明整体重构的数据质量较好。

图8中对各个区间相对误差所占的比例统计，发现相对误差在5%以下时所占比例整体最大，其中缺失率最低的2020年1月所占比例最高，缺失率最高的2011年1月所占比例最低。其他相对误差范围均有类似结论，但随着范围的增加，所占比例越来越低。也即各范围所占的比例与缺失率存在一定关系，同时表明重构数据质量越差。

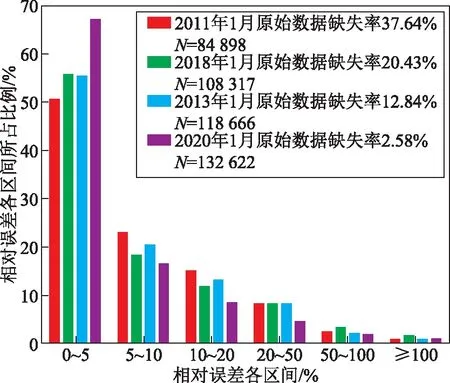
图8 不同年份1月整体重构与原始数据相对误差各区间所占比例

2.5 重构数据与缺失率相关性

图8 仅针对4个年份的1月分析了不同缺失率下整体重构数据与原始数据相对误差的比例情况，不具有普遍性，因此研究2009—2020年144个月各区间相对误差所占比例与数据缺失率之间的关系，可以得出较为普适的结论。图9(a)、图9(b)和图9(c)分别是相对误差在0～5%、0～10%和0～20%区间的占比与数据缺失率之间的散点图。结果表明，各区间所占比例与缺失率都存在一定的负相关关系。其中：相对误差0～5%区间，相关系数R为-0.550 9(P<0.01，通过显著性检验)；相对误差0～10%区间，相关系数R为-0.534 9(P<0.01，通过显著性检验)；相对误差0～20%区间，相关系数R为-0.499 3(P<0.01，通过显著性检验)。随着相对误差区间的增加，其负相关性以微弱趋势逐步减弱，低区间相对误差所占比例对重构数据质量具有显著影响。数据缺失率越高，重构数据质量越差。

图9 整体重构各区间相对误差所占比例与缺失率散点图

3 结束语

本文利用南海海域2009—2020年多传感器融合Chl-a浓度月平均遥感数据，采用DINEOF方法对数据进行整体重构和缺失点重构，对比分析了两种重构方式的数据质量。研究表明，在数据缺失点上，整体重构和缺失点重构两种方式得到的重构数据相同，而在非数据缺失点上，缺失点重构保留原始数据进行计算，整体重构不保留原始数据进行重新计算。虽然从CORR、RMSE和BIAS等统计数据和密度散点图结果来看，原始数据与整体重构数据匹配的数据点除少数数据外，均保持高度一致性，重构数据保留大部分原始数据的信息，但数据质量仍有一定程度的下降。此外，从时空分布图分析，整体重构数据的平滑比缺失点重构范围更广更明显，体现在全海域，且缺失率越高的海域，平滑越突出。因此，整体重构数据质量比缺失点重构数据质量略差。

由上可知，采用DINEOF方法对Chl-a浓度遥感数据进行重构时，应采用缺失点重构方式，以避免整体重构方式造成的原始数据平滑。而整体重构方式仅用于验证重构数据在缺失点数据的有效性。这样能在保留原始数据的前提下科学高效地获取重构Chl-a浓度遥感数据。需要注意的是，虽然本文所采用的数据重构方法能够很好地填补原始数据的缺失，但原始数据的缺失率越高，重构后的数据质量越低。

虽然DINEOF算法具有自适应、高效和不限制海域等优点，但其具有低通滤波功能，重构过程会丢失局部信息。国内外学者在DINEOF算法的基础上进行了改进，弥补局部精度的损失具有重要意义，但依然存在一些各自的问题。因此，如何解决这些问题，仍然是当今研究的重点内容。