基于改进PSO-BP的模糊PID烧结炉温度控制
2022-03-01王彦勇
□□ 王彦勇
(山西职业技术学院,山西 太原 030006)
引言
滚磨光整加工是机械加工领域的一类基础性制造工艺技术,可用于提高零件表面质量并改善零件使用性能。在滚磨光整加工过程中,滚抛磨块是影响加工效果和加工效率的关键因素[1]。烧结型磨块在滚抛磨块中占比较大,使用较为广泛,其烧结过程中炉温控制的精度是影响磨块质量的关键因素。
烧结炉是工业生产过程中常用的加热装置,温度跟随控制的精度与产品的使用寿命和质量息息相关。但由于炉内结构和温度变化的不稳定性、外界干扰的复杂性,严重影响了温度跟随控制的精度。传统的PID控制方法操作简单、易于实现,广泛应用于烧结炉温度控制系统。温度控制系统受较多参数的影响导致其抗干扰能力弱、跟随性差、控制精度低。针对传统PID控制存在的问题,诸多学者将机器学习、人工智能等方法引入其中。YE Y等[2]针对非线性液压系统,提出利用粒子群算法(particle swarm optimization,PSO)优化PID的控制方法。ZHANG F X等[3]采用改进的状态转移算法优化PID参数,提出一种基于模糊逻辑的分数阶模糊PID控制方法。Cherrat N等[4]采用模糊系统整定PID参数,并利用梯度下降算法优化模糊系统参数,仿真结果表明自适应模糊PID的有效性。
分析上述研究方法可知,常规预测方法预测精度较低、参数整定不合理,导致调节时间增大,稳态精度降低。粒子群算法易于陷入局部最优。因此,提出了一种基于改进PSO-BP的模糊PID烧结炉温度控制方法。该方法采用改进粒子群算法整定优化PID参数,并利用BP神经网络预测下一时刻温度,将超前温度信息作为改进粒子群算法的适应度函数参数,提前调整PID控制器参数,最后通过模糊推理在温度控制过程中,在线调整PID参数,加强温度控制的跟随性。
1 基于改进PSO-BP的模糊PID控制器
为了解决使用固定参数控制的PID控制器响应速度慢、跟随性差、超调量大的问题,提出采用改进PSO对PID控制器参数进行整定,并利用BP神经网络预测下一时刻温度,将超前温度信息作为改进PSO的适应度函数参数,提前调整PID参数,减小响应时间。通过模糊推理在温度控制过程中,实时调整PID参数,加强温度控制的跟随性。基于改进PSO-BP的模糊PID控制器原理如图1所示。
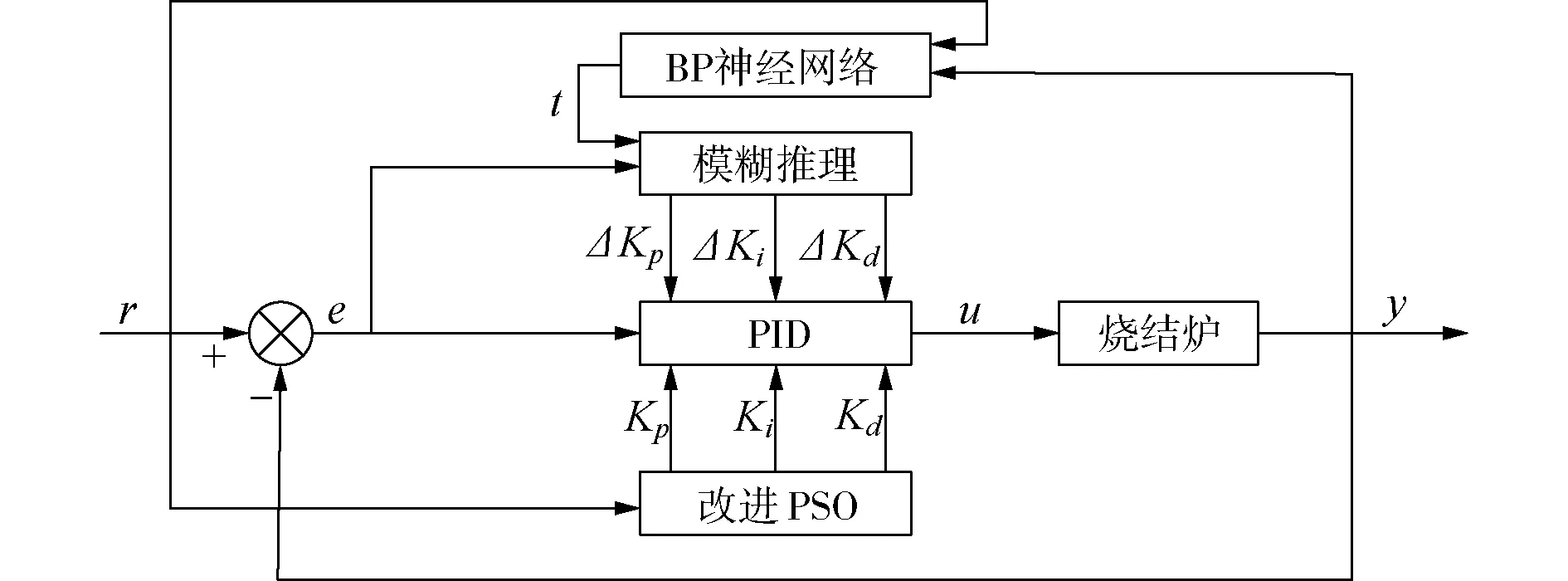
图1 基于改进PSO-BP的模糊PID控制器原理
图1中,r为设定温度;u为PID控制器输出;y为实际输出温度;e为实际温度与设定温度的误差。整个控制器由4部分组成:
(1)PID控制器:通过Kp、Ki、Kd闭环控制被控对象。
(2)BP神经网络:通过当前温度与控制参数信息预测下一时刻温度。
(3)改进粒子群算法:通过设定温度对PID的Kp、Ki、Kd三个参数寻优。
(4)模糊推理:通过e和BP的预测温度t在线调整PID参数。
1.1 BP神经网络
BP神经网络是一种误差反向传播的神经网络。如果隐含层节点数足够,BP神经网络可以确定任何非线性映射方程并具有优异的泛化性,这是BP神经网络最大的优势。BP神经网络典型的结构如图2所示。BP神经网络包含3层:输入层、隐含层和输出层[5]。

图2 BP神经网络典型结构图
如果隐含层的传递方程为f1(·),输出层的传递方程为f2(·),则隐含层的输出为式(1)。
(1)
输出层的输出为式(2)。
(2)
式中:n——输入层节点数目;
q——隐含层节点数目;
m——输出层节点数目;
vki——输入层节点i到隐含层节点k的权重;
wjk——隐含层节点k到输出层节点j的权重。
在温度预测过程中,选择输入层节点数为3,分别为r(t)、u(t)和y(t);隐含层节点数为5,传递函数为sigmoid函数;输出层节点数为1,输出为y*(t+1)。
1.2 改进粒子群算法
粒子群优化算法是模拟鸟类等群体觅食而提出的[6]。传统的粒子群算法是在n维空间中,设种群由m个粒子构成,即X=[x1,x2,…,xm],第i个粒子的位置定义为xi=[xi1,xi2,…,xin]。第i个粒子的历史最优位置为Zbest,i=[zi1,zi2,…,zin],速度为vi=[vi1,vi2,…,vin]。种群的最优位置Zg,best=[zg1,zg2,…,zgn]。
在每次迭代过程中,粒子速度与位置按照式(3)、(4)所示的方式更新。
(3)
(4)
式中:i——粒子序号;
d——粒子维数序号,d=1,2,…,n;
w——惯性权重;
k——迭代次数;
r1、r2——0,1之间的随机数;
c1、c2——学习因子。
每个粒子根据第k次迭代的速度,利用种群最优位置和自身最优位置得到自身第k+1次迭代的速度。在进行速度更新之后再计算粒子的更新位置。其中,最优位置通过计算每个位置的适应度函数值确定。本文选择ITAE指标为适应度函数[7],公式见式(5)。

(5)
在采用PSO对PID参数寻优的过程中,为了避免陷入局部最优[8],参考遗传算法中“变异”概念,将粒子变异引入PSO中,构建变异粒子群寻优算法。即在参数寻优过程中,粒子以一定的概率发生变异,且变异的概率随着迭代次数的增长而减小。该策略既可以避免粒子过早陷入局部最优,还可以防止由于变异概率过高,粒子无法收敛。具体的变异策略见式(6)和式(7)。
(6)
p(k)=p(N-k)/N
(7)
式中:xik——第k次迭代后第i个粒子;
xmax——粒子的最大位置;
c——变异因子,满足0≤c≤1;
rand()——随机函数,生成[0,1]的随机数;
p(k)——变异概率;
p——初始变异概率;
N——最大迭代次数;
K——当前迭代数。
惯性权重w能够均衡PSO的全局搜索能力和局部搜索能力。w越大,全局搜索能力越强;w越小,局部搜索能力越弱[9]。因此,动态调整w可以使粒子具有更好的收敛性。本文提出的w动态公式见式(8)。
wk=wk-1-(wk-1-wmin)·z
(8)
式中:wk——第k次迭代的惯性权重;
wk-1——第k-1次迭代的惯性权重;
wmin——惯性权重的最小值;
z——动态调整因子,满足0≤z≤1。
1.3 模糊推理
模糊推理主要包含模糊化、知识库、推理机和解模糊化[10]。本文中,模糊推理的前件变量为温度误差e和BP的预测温度t,后件变量为ΔKp、ΔKi、ΔKd。首先,根据前件变量和后件变量的论域范围进行模糊化。由于前件变量e和t的取值范围为[-25,25],后件变量ΔKp、ΔKi、ΔKd的调整范围分别为[-5,5]、[-0.06,0.06]和[-0.3,0.3],因此,针对烧结炉温度在运行过程中的调整范围,本文采用三角形隶属度函数将论域范围[-3,3]模糊为{NB,NM,NS,ZO,PS,PM,PB},分别表示负大、负中、负小、零、正小、正中、正大[11]。
对ΔKp、ΔKi、ΔKd调解时通过制定合适的模糊控制规则,根据检测到的温度误差e和预测温度t,先模糊化,再利用模糊推理以及解模糊化计算出不同的调节量ΔKp、ΔKi、ΔKd,然后在线修正PID的参数,其计算公式见式(9)。
(9)
式中:Kp、Ki、Kd——PID控制器的参数;
K′p、K′i、K′d——PID控制器的初始参数;
ΔKp、ΔKi、ΔKd——调节量。
综上所述,依据专家及现场经验,设计参数ΔKp、ΔKi、ΔKd的模糊控制规则见表1~3。
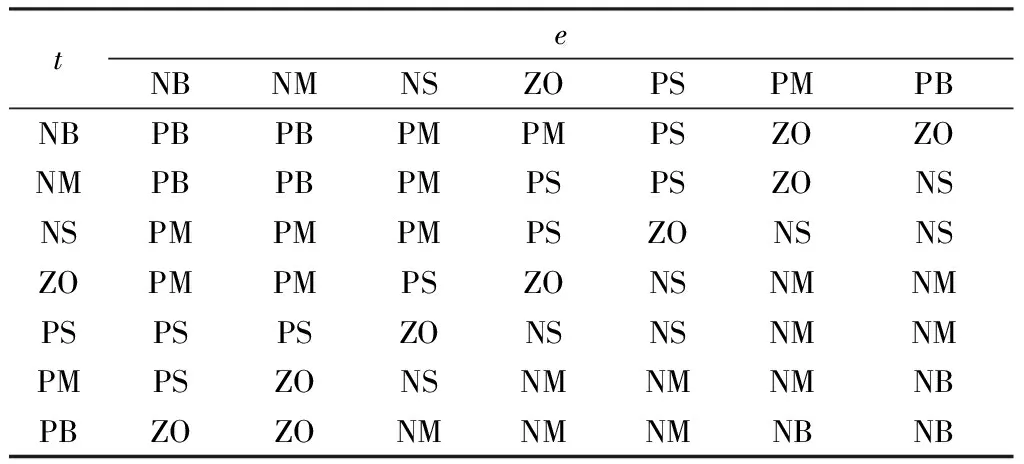
表1 ΔKp的模糊规则控制表
2 烧结炉温度控制系统测试及仿真结果分析
为了验证提出方法的准确性与有效性,采用滚抛磨块烧结炉与烧结炉温度数据进行试验,利用Matlab软件进行数据分析。
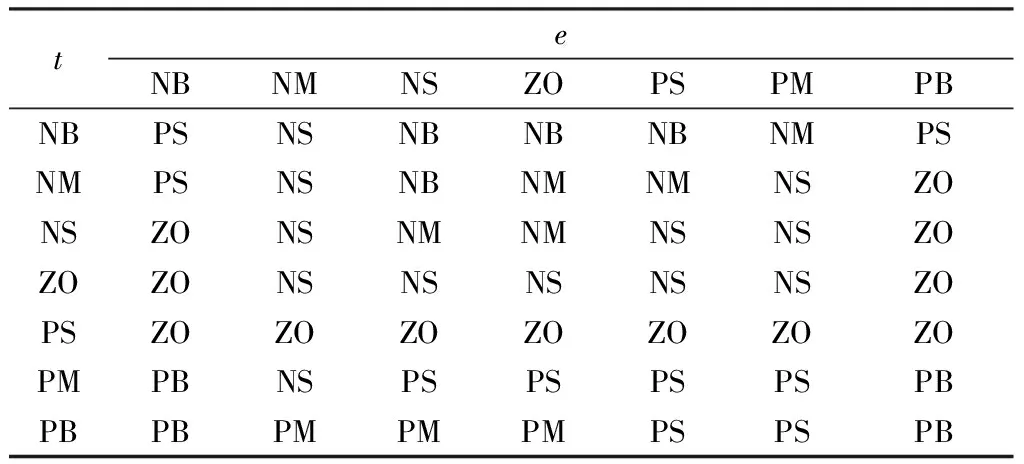
表3 ΔKd的模糊规则控制表
2.1 基于BP神经网络的烧结炉温度预测结果
采用2 000组具有时间序列的烧结炉温度数据作为模糊网络数据,其中前1 900组为训练样本,后100组数据作为测试样本,评估BP神经网络的预测精度。为了定量地评价神经网络性能,采用平均绝对百分误差(MAPE)、均方根误差(RMSE)和平均绝对误差(MAE)作为评价指标。最后的测试结果见表4。

表4 BP温度预测性能
由表4可知,BP神经网络预测烧结炉温度的平均绝对百分误差达到了0.76%,说明BP神经网络对温度的预测精度可以满足整个控制器要求。
2.2 基于改进PSO的PID参数优化结果
改进PSO的种群数m=100;最大迭代次数N=100;初始惯性常量w=0.9;惯性常量最小值wmin=0.4;学习因子c1=2,c2=3;变异概率p=0.4;变异因子c=0.6;动态调整因子z=0.3;Kp、Ki、Kd的搜索空间均为[0.000 1,5]。采用本文提出的改进PSO与原始PSO的最优粒子适应度变化曲线如图4所示。
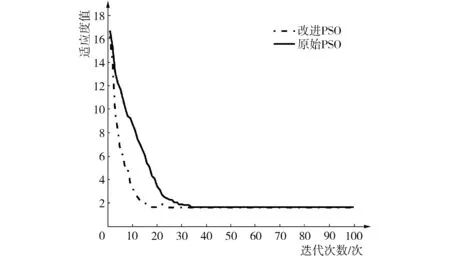
图4 粒子适应度变化曲线
由图4可知,改进PSO收敛速度优于原始PSO,迭代次数达到20次时,适应度函数值就达到了稳定状态,验证了改进PSO的必要性和有效性。在PID参数寻优时具有更好的收敛性。
2.3 温度控制实测结果
以烧结炉温度要求进行试验,分别利用传统PID控制器和改进PSO-BP的模糊PID方法进行温度控制,每隔5 s采集1次温度数据,绘制温度趋势变化图如图5所示。
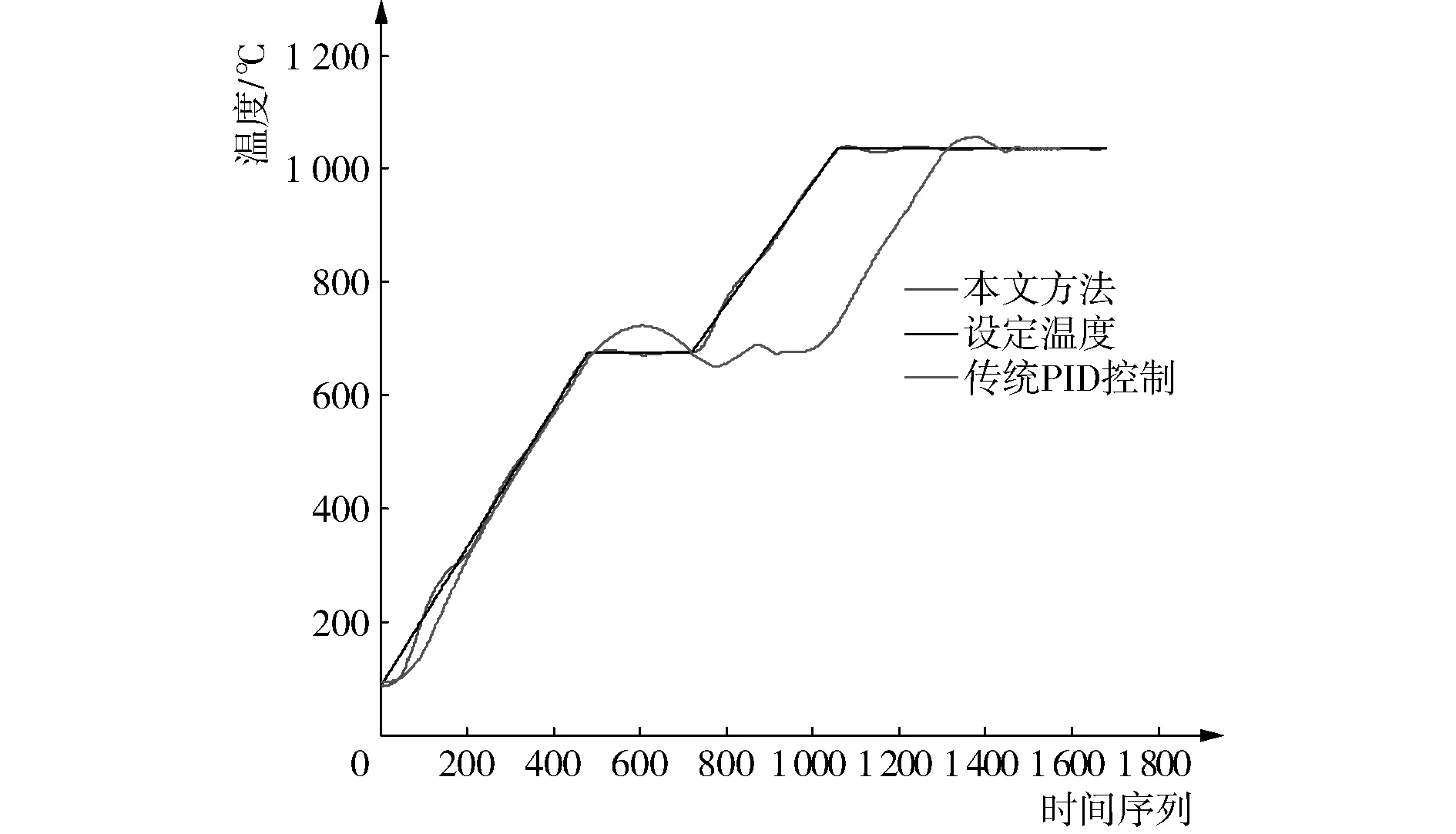
图5 不同方法温度控制比较
由图5可知,改进后的PID方法比传统PID具有更快的响应速度、跟随性和更小的超调量。为了定量分析两种方法的性能,列出两种方法的各性能指标,见表5。

表5 两种方法温度控制方法的性能比较
由表5可知,改进后的PID方法在烧结炉温度控制过程中各项性能均优于传统PID控制方法,验证了改进方法的准确性和有效性。
3 结论
针对目前烧结炉温度控制系统响应速度慢、跟随性差等问题,本文提出了一种基于改进PSO-BP的模糊PID烧结炉温度控制方法。该方法实现简单,可在线调整PID参数。采用大量现场数据进行验证可知,改进后的PID控制方法的静态特性和动态特性均优于传统控制方法,且具有响应时间快、跟随性强、调节时间短等优点。
