基于响应面法的磁悬浮开关磁阻电机优化设计

邵淋晶， 朱海浪， 张巍

(南京工程学院 电力工程学院，江苏 南京 211167)

0 引 言

飞轮储能(flywheel energy storage,FES)是一种高效的物理储能装置，具有储能密度大、传输效率高和寿命长等优点，在混合动力车辆、不间断电源和航空航天等领域具有广阔的应用前景[1]。电机作为FES的核心部件，是FES研究中的热点和难点。磁悬浮开关磁阻电机(bearingless switched reluctance machine,BSRM)结合磁轴承与开关磁阻电机的双重优点，集转子驱动和悬浮支撑于一体，可简化系统结构，提高临界转速与系统可靠性[2]。单绕组磁悬浮开关磁阻电机(single winding bearingless switched reluctance machine, SWBSRM)与传统磁悬浮开关磁阻电机相比，结构简单，定子上仅有一套绕组用来同时产生悬浮力和转矩。克服了双绕组之间的磁链干扰。SWBSRM内部磁场复杂且具有复杂的非线性关系，因此合理优化设计电机结构参数，改善电机运行性能是电机设计中的关键问题。文献[3]采用理论分析和有限元计算相结合的方法对BSRM优化设计，该方法在优化过程中需要多次调用有限元计算模型，计算效率低下。文献[4]利用支持向量机(support vector machine, SVM)对样本数据空间进行模型训练，同时用遗传算法进行参数寻优，提高了算法优化速度，但是SVM在小样本数据下建模精度一般。文献[5]采用和声混沌搜索算法对电机的各结构进行参数优化，引入权重因子来定义目标函数，实现电机参数的多目标寻优，但和声混沌算法关键参数的选取缺乏理论基础，选取具有主观性。

针对上述问题，本文以12/8极单绕组磁悬浮开关磁阻电机为对象，在阐述电机基本结构及工作原理基础上，建立电机的二维有限元参数化模型。采用中心复合设计(central composite design, CCD)试验设计进行样本空间构建及有限元仿真，获得电机平均转矩和悬浮力的响应面方程作为优化模型；同时，引入遗传粒子群算法进行电机性能的多目标优化，获取最优参数组合；最后将优化前后电机的性能进行对比和仿真分析，验证所提多目标优化方法的有效性。

1 电机工作原理及电磁有限元建模

1.1 电机结构与原理

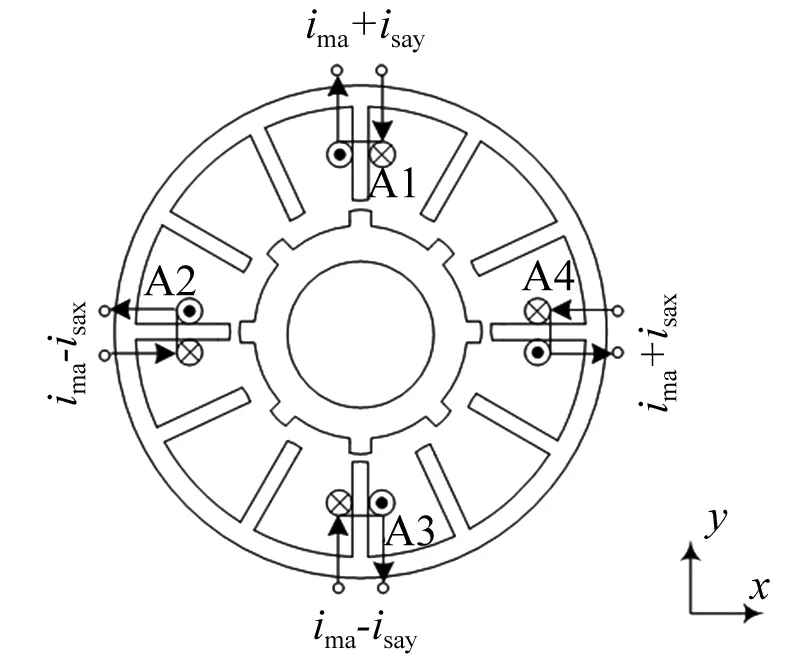
图1 SWBSRM结构示意图

图1为三相12/8极BSRM的结构示意图。图1中仅给出A相绕组分布图，B相和C相绕组沿A相绕组逆时针方向30°和60°放置，配置与A相完全一致。每个定子极上只有一套独立控制的绕组，A相绕组逆时针方向依次为A1、A2、A3和A4，四极绕组互不相连且匝数相同。每极定子绕组电流可等效为转矩电流分量ima和悬浮电流分量isax、isay之和。转矩电流产生转矩控制磁场，驱动转子旋转。同时转矩电流产生偏置磁场，与悬浮电流分量isax、isay差动励磁，打破偏置磁场的平衡，形成x、y方向的悬浮控制磁场，进而产生x、y方向的悬浮力。通过改变悬浮电流分量的大小和方向，可以产生任意方向和大小的悬浮力，实现转子的稳定悬浮。B相与C相的悬浮原理和A相一致。

1.2 有限元仿真参数设计

在Ansys/Maxwell中搭建SWBSRM二维参数化有限元模型，电机的初始各项关键结构参数如表1所示。

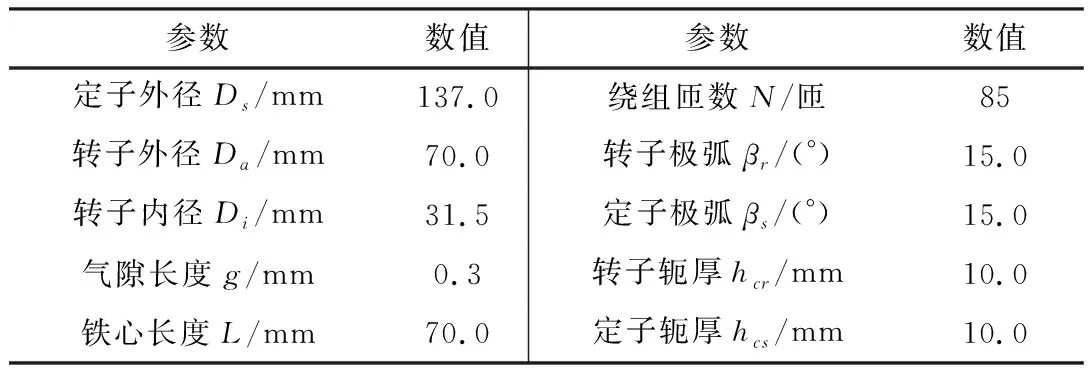
表1 SWBSRM初始结构参数

利用二维有限元瞬态场对电机进行仿真分析，有限元仿真过程中设置转矩电流激励ima=4.7 A。悬浮电流激励isax=isay=1.88 A。

2 试验结果和分析

2.1 响应面试验

在SWBSRM体积不变的前提下，提升电机的转矩与悬浮力，具有重要实际意义。由等效磁路法所得电机悬浮力及电磁转矩表达式可知，各定转子齿极下气隙磁导对电机输出性能影响显著[6-7]。SWBSRM定转子齿形参数会改变磁通传导路径，从而改变磁路磁导，进而影响电机整体的转矩和悬浮输出性能。因此，为进一步提升电机转矩和悬浮出力，需对SWBSRM的定转子齿形参数优化设计。由文献[8-9]研究可知，定子极弧βs、转子极弧βr与平均悬浮力Favg，平均转矩Tavg呈现复杂的非线性关系。故本文选取定子极弧βs、转子极弧βr作为待优化变量，电机一相导通区间内平均悬浮力Favg和平均转矩Tavg作为优化目标。在任何转子位置，电机需具有正、反向的自启动能力，即电机定、转子极弧的确定，需要满足以下条件：

(1)

综上，在考虑实际仿真可行条件下，初步确定电机的定、转子极弧的优化范围分别[15°,25°]，[15°,25°]。以定子极弧βs和转子极弧βr为自变量(X)，以平均悬浮力Favg和平均转矩Tavg为响应值(Y)，应用多元线性回归方法建立响应面数学模型。采用二阶响应面模型对SWBSRM的平均悬浮力和平均转矩进行拟合，响应面方程为：

(2)

式中:β为待定系数;x1，x2分别为定子极弧βs与转子极弧βr；ε为拟合误差。利用最小二乘法即可求解出各待定系数。式(2)的响应面模型可用矩阵表示为：

Y=Xβ+ε

(3)

使用最小二乘法，可以求出回归系数β的估计值b：

b=(XTX)-1XY

(4)

拟合回归模型可表示为：

Y=Xb

(5)

鉴于优化参数变化范围各不相同，将各参数实际值进行编码转换以方便后续处理，转换规则如式(6)所示。

(6)

式中:xi为所选优化参数实际值;Xi为参数编码转化值。

本文设计参数变量与相应的编码转换值如表2所示。

表2 应用CCD设计参数变量

利用有限元方法得出不同的试验设计的平均悬浮力(Favg)和平均转矩Tavg，如表3所示。

表3 试验设计方案及结果

基于最小二乘法估计，最终拟合所得的二阶响应面数学模型方程为：

(7)

(8)

2.2 回归与方差分析

对已得到的SWBSRM的平均悬浮力和平均转矩的响应面数学模型进行方差分析，如表4和表5所示。

由表4和表5可知，两模型的P值均小于0.001，表明模型的拟合度较好，适应性显著。且两模型的复相关系数R2分别为0.999和0.974，均大于0.9，表明因素变量与各个响应之间的关系显著，数据规律能被模型较好的反映。

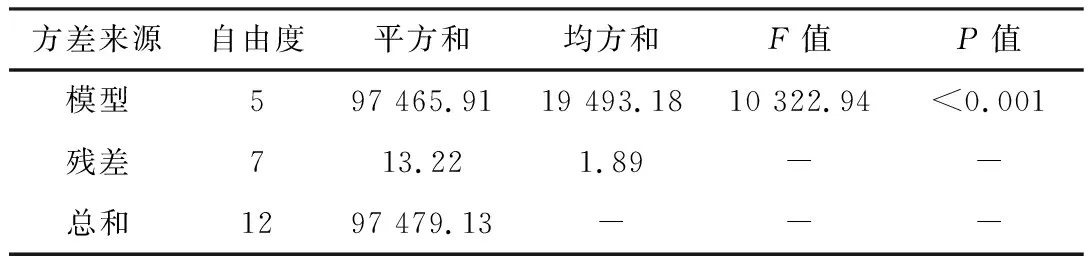
表4 悬浮力模型方差分析表

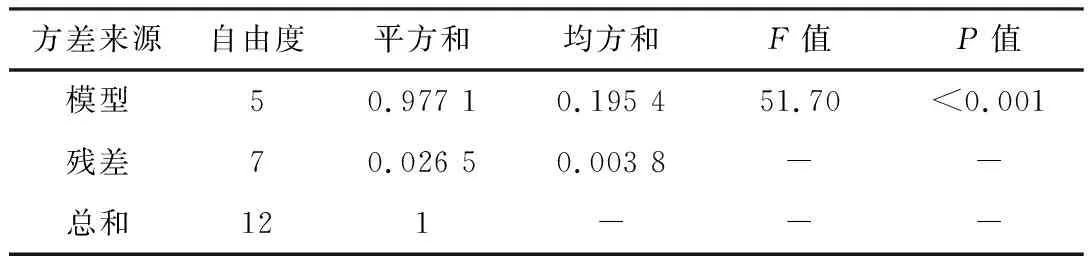
表5 转矩模型方差分析表

3 基于GAPSO的多目标优化

3.1 遗传粒子群综合算法

针对传统粒子群算法(particle swarm optimization,PSO)易陷入局部最优的特点，本文提出具备双重学习功能的遗传粒子群综合算法(GAPSO)：以经典PSO算法为主体，在迭代过程中引入遗传算法中交叉和变异操作对参数寻优。个体最差值pbi=(pbi1，…,pbid,…,pbiD)T，全局最差值gb=(gb1,…,gbd,…,gbD)T，其速度，位置更新为：

(9)

图2 算法流程图

式中：vid、xid分别为粒子i的速度和位置的第d维分量大小；k为迭代次数；ω为惯性权重；c1、c2为学习因子；r1、r2为约束因子。GAPSO基本流程图如图2所示。

3.2 GAPSO优化过程

为获取使电机转矩和悬浮力性能均为最优的参数组合，需要在优化目标之间进行协调和折中，因而构建电机性能多目标优化函数为：

f=αTavg+βFavg

(10)

式中:α和β分别为平均转矩和悬浮力的权重系数。为避免电机转矩和悬浮力之间的数量级差对于目标函数的影响，两个系数分别取另一性能均值，即α=180.72，β=2.00。

利用响应面拟合的优化模型，寻求目标函数的最大值。优化过程中，参数设置如下：粒子个数50，迭代次数为10 000，惯性权重ω从0.9衰减至0.4，学习因子c1=c2=2，约束因子r1=r2=0.72，交叉概率为0.5，变异概率为0.1。

3.3 SWBSRM结构参数优化结果及分析

图3和图4给出了在转子无偏心、电流激励相同大小下优化前后电机的转矩性能和悬浮性能。0°为定、转子极中心线对齐位置角。由图3和图4可知，在不同转子位置角下，悬浮力和转矩均得到了明显的提高。表6给出了SWBSRM优化前后电机结构参数和输出性能对比。进一步分析可知，参数优化后的平均转矩和悬浮力分别为2.460 7 N·m和435.628 7 N与优化前平均转矩2.003 6 N·m和悬浮力180.721 5 N相比，分别提高了22.81%和141.04%。验证了本文所提的SWBSRM结构多目标优化设计的有效性。

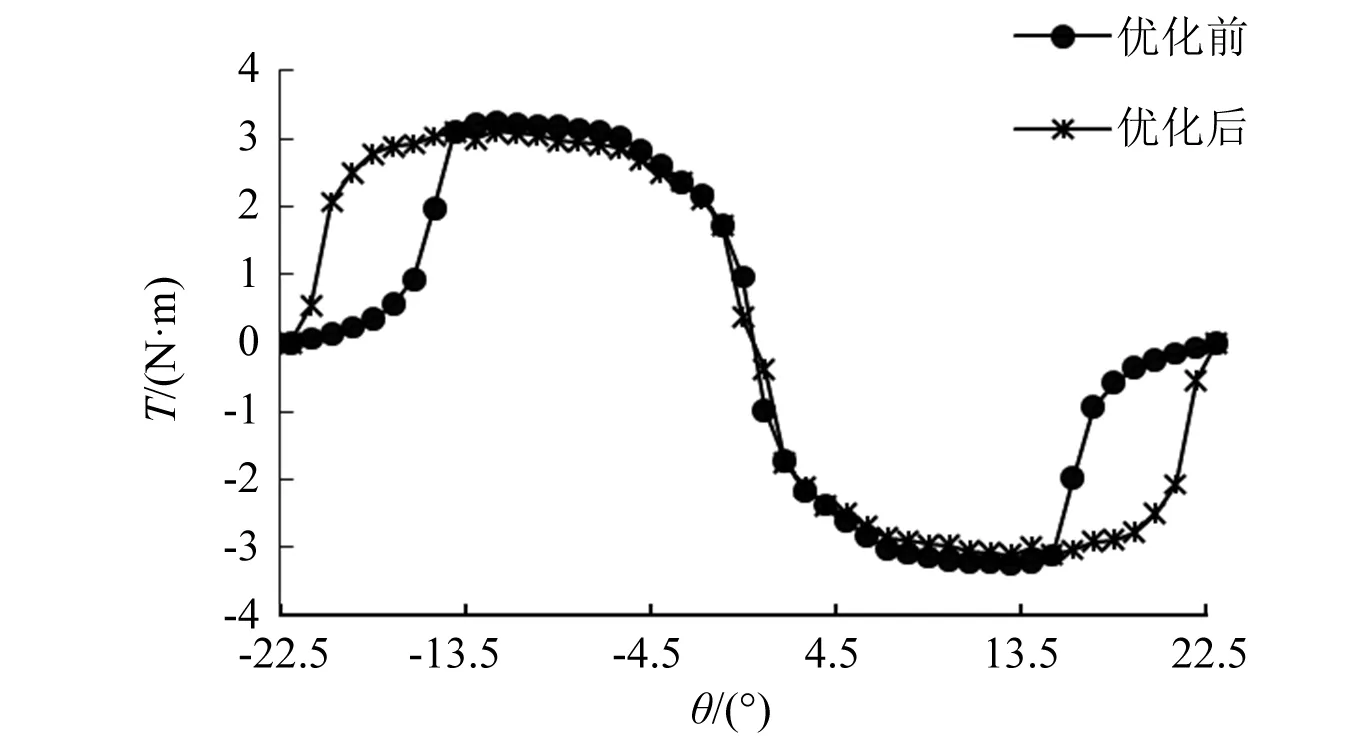
图3 优化前后转矩对比

图4 优化前后悬浮力对比

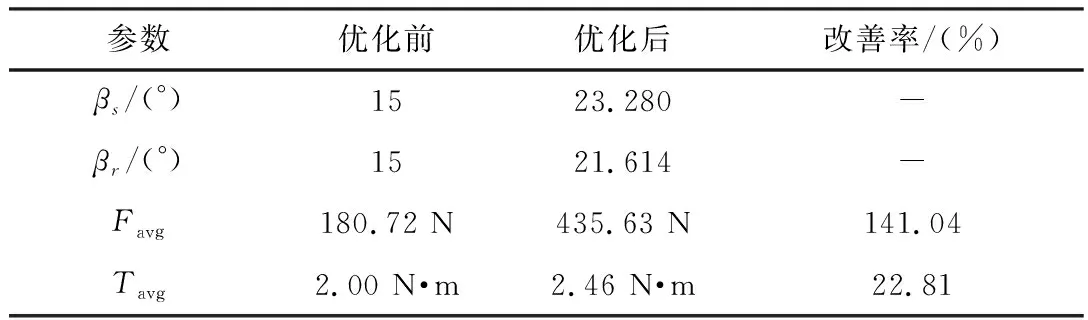
表6 参数优化结果

4 结束语

本文针对应用于飞轮储能系统的SWBSRM，提出了一种悬浮力和转矩协同优化的多目标优化方案。在确定电机的优化参数和优化目标的基础上，利用CCD试验设计方法构造出试验样本点，通过Ansys/Maxwell有限元试验计算样本响应值，结合响应面法拟合出平均悬浮力和平均转矩的优化模型。针对该优化模型，结合遗传粒子群综合算法，获得电机平均转矩和悬浮力协同更优的参数组合。仿真试验表明：优化后电机相比于原电机在全周期范围内悬浮力和转矩均有所增加；验证了多目标优化设计的有效性。同时本文采用的多目标优化设计方法为电机本体参数优化提供了一种新思路。