基于遗传算法和粒子群优化的列车自动驾驶速度曲线优化方法

2022-03-01朱爱红

计算机应用 2022年2期

张京，朱爱红

（兰州交通大学自动化与电气工程学院，兰州 730070）

0 引言

列车自动驾驶（Automatic Train Operation，ATO）系统最主要的功能就是自动调节车速，让列车平稳地运行并能准确停靠在车站的指定位置。ATO 系统在给定约束条件下寻找出满足要求的目标速度曲线，生成最优控制策略，指导列车沿着最优速度曲线运行，因此，列车速度曲线的优劣直接影响自动驾驶系统的性能。为得到最优目标速度曲线，国内外不少学者对此展开了广泛的研究。文献［1］通过研究列车在不同坡度的线路上的惰行工况点位置的选择，来实现降低运行能耗的目的；文献［2］通过动态规划和二次规划对列车节能运行过程进行优化研究，降低了运行能耗；文献［3］采用遗传算法（Genetic Algorithm，GA）来寻找最佳工况转换点位置来优化列车目标速度曲线，达到了降低能耗的效果；文献［4］通过人工蜂群算法与操纵工况序列结合，找出最佳工况切换转换点的位置和速度，达到了降低能耗的目的。以上研究都是基于降低列车运行过程中能耗的单一目标优化研究，随着列车ATO 系统的发展，以精准停车、准时、舒适以及节能等多目标为新的发展方向；其次采用的单一优化算法，很难避免算法本身存在的不足。文献［5］通过搭建列车ATO 运行多目标优化模型，将列车的最优目标速度曲线通过遗传算法来寻优求解，取得了一定的优化效果；文献［6］利用改进的多目标微粒群算法对列车控制工况序列及运行距离进行优化研究，获得最优的控制策略。上述研究均未考虑列车过分相区带来的影响，不考虑分相区惰行的操控方案，会产生较大的误差，不具有实际应用价值。针对上述问题，本文对粒子群算法进行改进，采用非线性动态惯性权重和改进的加速度系数，并将遗传算子融入其中，构成一种GAPSO（Genetic Algorithm and Particle Swarm Optimization）算法；同时将过分相区断电惰行纳入控制工况，在前人研究的基础上，对工况切换点的速度进行优化，寻找满足多目标要求的一组最优速度值，生成一条最优速度曲线，指导列车运行，实现列车自动驾驶多目标优化。

1 列车ATO多目标模型的构建

1.1 列车动力学模型

对运行中的列车进行受力分析，为简化研究对象，将列车理想化为一个刚性质点［7］，构建其动力学模型，如式（1）所示：

其中：t、s、v依次为运行时刻、运行位置和运行速度；a、ε分别为加速度和加速度系数；w0为基本阻力；u表示牵引力或制动力；γ为车轮回转质量系数；a、b、c是与车型相关的经验常系数；wj为附加阻力。

1.2 列车ATO运行多目标优化模型

1.2.1 精准停车模型

其中：S为实际停车点位置；S0为线路的目标停车点位置；Ks是以S、S0的差值作为精准停车指标，通常要求停车误差在0.3 m 范围内［8］。

1.2.2 准时性模型

其中：T为全程实际的运行时间；T0为线路的目标运行时间；Kt是以T、T0的差值作为准时性衡量指标。一般情况下，列车运行时间误差不超过线路的目标运行时间的5%，均视为满足准时性要求［9］。

1.2.3 舒适性模型

舒适性表示在列车运行期间对乘客的冲击率，通常用列车运行时的纵向加速度相较于时间的变化率来定义，可以用如下模型表示：

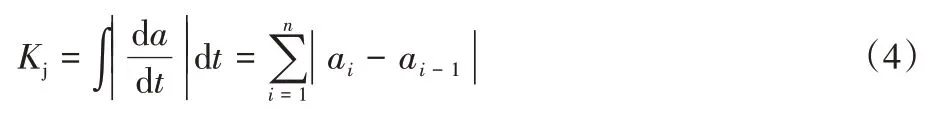
其中：Kj表示衡量列车运行时的舒适度指标，Kj越大，代表乘车舒适度越差；ai为第i个控制工况下列车的加速度。

1.2.4 能耗模型

在列车行车途中，耗能的主要源头是列车的牵引力和制动力克服阻力做功，故可得出能耗模型［10］：

其中：F为列车运行过程中的牵引力；v为车速；t为到站停车所需的时间；B为列车运行过程中的制动力；ξM为牵引所需电能换算成电能的乘积因子；ξB为制动时所需的机械能换算成电能的乘积因子。因为研究重点在于行车过程，因此，可采用以下模型：

其中：Ke为列车能耗的衡量指标；Si和ai分别表示第i个工况下的列车的位移和加速度。

综上所述，解决列车ATO 运行多目标优化问题，就是根据式（1）搭建的列车动力学模型，求出一组满足各个性能指标的工况序列{ui}i=1，2，···，k和k-1 个工况转换点速度，使得整体性能达到最优［11］，建立如下列车ATO 运行多目标优化模型：

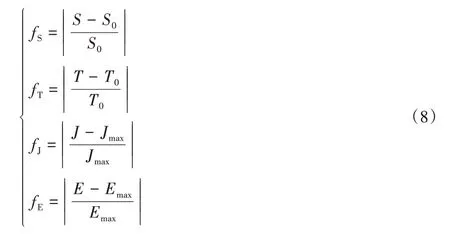
本文采用变化率的形式来对各优化指标进行统一量纲，如式（8）所示：

沿用加权求和的方法，通过衡量不同目标所占的比重，给它们赋予不同权重，将其转化为单目标优化问题，得到如式（9）所示的总体评价指标函数：

其中：Jmax、Emax分别为节时模式下的舒适度值和能耗；fS、fT、fJ、fE分别为Ks、Kt、Kj、Ke统一量纲后的优化指标；S、T、J、E分别为实际停车点位置、运行时间、舒适度以及能耗；ω1、ω2、ω3、ω4依次为各优化目标对应的权重系数且ω1+ω2+ω3+ω4=1。由于适应度值越高，衡量各个目标的总体指标越优，故适应度函数可表示为：

1.3 列车控制策略的分析

列车的整个运行过程是由多个工况组合而成的，主要分为以下三种：牵引、惰行以及制动［12］。对于工况的切换不是任意进行的，需符合如表1 所示的转换原则。

表1 工况转换原则Tab.1 Principles of operating mode changing

列车各个工况之间的切换必须按照特定的工况转换原则进行，初始阶段为牵引工况，终点停车时为制动工况。列车工况转换前，需要在该工况下继续运行一段距离，避免频繁地进行工况切换，从而确保了运行的平稳和舒适［13］。列车受到的合力决定了运行状态，通过牵引、惰行、制动工况控制列车的受力完成整个自动驾驶过程，把这些完成整个运行过程的工况组合称为列车运行控制策略。常见的列车运行控制策略主要有最小时分控制策略、最节能控制策略和混合控制策略［14］，如图1 所示。

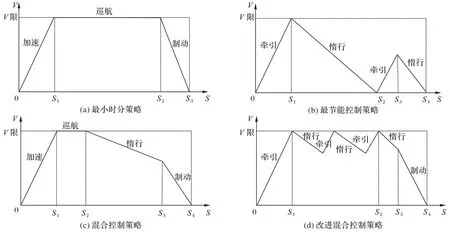
图1 列车ATO运行控制策略Fig.1 Train ATO operation control strategy

最小时分策略在启动阶段，以最大牵引力运行，达到限速后，贴近限定速度，以一定的速度裕量控制列车巡航运行，在到站停车阶段以最大制动力减速停靠；运行效率高，但能耗和舒适度较差。最节能控制策略是通过尽可能地延长惰行时间，缩短制动工况的运行距离。虽然能耗最低，但严重影响运行效率，不符合铁路运输要求。混合控制策略是结合上述二者的情况，考虑能耗和运行效率，适当采用巡航来提高全程的平均运行速度，一定程度上降低能耗和提高了运行效率，但在线路中间有较大的速度变化时，或限速情况较为复杂时，无法保证能耗最小、效率最高。因此改进混合控制策略，充分利用线路情况，采用牵引、惰行、制动工况对速度进行精确控制，实现降低能耗并兼顾运行时分要求。列车的控制工况往往是不确定的，可以根据优秀司机驾驶的经验以及线路的具体情况，事先拟定多种操纵工况转换策略来指导行车过程［15］。

2 结合遗传算子的改进粒子群混合算法

2.1 改进粒子群优化算法

粒子群算法具有编码难度低、种群粒子进化速度快、收敛精度高等特点，属于一种并行启发式随机搜索算法，在优化设计等问题中被广泛采用。在算法优化过程中，个体通过记录两个“极值”（pbest，gbest）不断更新自己的位置和速度，实现种群不断进化。速度和位置通过式（11）～（12）更新：

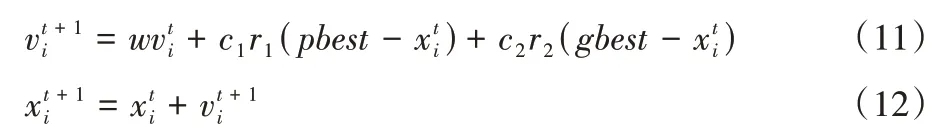
2.1.1 对惯性权重系数的改进

其中：wmax、wmin分别为惯性权重取值范围的上界和下界，通常取值为wmax=0.9，wmin=0.4；f、fmin、favg分别为当前粒子的适应度值、种群中最小适应度值、种群平均适应度值。

2.1.2 对学习因子的改进

c1和c2为种群粒子的学习因子，分别起到调节个体学习能力和群体学习能力的作用。c1取值过大时，会导致过多粒子聚集于局部区域，影响全局寻优效果；c2取值过小时，粒子会过早收敛局部最优。因此，最佳的寻优策略是：在初期尽可能地让粒子在解空间飞跃遍历，维持粒子的多样性；在后期，为避免局部最优的影响，粒子的寻优速度应保持恒定。通常情况下，c1、c2采用固定值，不利于算法的寻优效果且误差较大，本文对c1和c2进行改进，更新策略公式为：

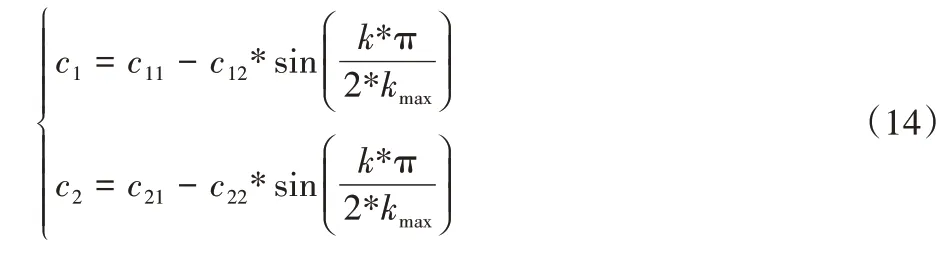
其中：k为当前的进化次数；Kmax为种群的最大进化次数；c11、c12为学习因子c1的迭代取值的上下界；c21、c22为学习因子c2的迭代取值的上下界。通过文献［17］的测试分析，c11=2、c12=1、c21=1、c22=1 算法寻优能力最佳。

2.2 结合遗传算子的改进粒子群算法

粒子群算法和遗传算法均属于群智能算法的范畴，在解决全局优化问题时具有广泛的应用。前者具有较好的探索精度及较快的收敛速度，但容易陷入局部最优；后者由于遗传算子的特殊性，使其具有强大全局搜索能力，但收敛速度慢。结合二者优点，将遗传算子引入到改进后粒子群算法中，构建一种包含遗传算子的改进粒子群优化算法，即GAPSO。

1）选择算子的操作实现：根据适应度值对粒子作出评价，以一定的比例从中挑选出优质个体，确定杂交池的大小。

2）杂交算子的操作实现：将经过筛选后的粒子组成杂交池，在其中随机挑出相互独立的两个粒子进行杂交，直到杂交池内所有粒子完成杂交。新个体的位置和速度通过式（15）～（16）更新：

国务院总理李克强日前签署国务院令，公布修订后的《中华人民共和国个人所得税法实施条例》。修订后的个人所得税法实施条例自2019年1月1日起与新个人所得税法同步施行。其中：国务院印发个人所得税专项附加扣除暂行办法通知，6项专项附加扣除包括规定的子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等。税务总局局长称，全力以赴确保个税改革平稳落地，让纳税人及时享受专扣政策红利。

3）变异算子的操作实现：采取高斯变异，如式（17）所示。按照变异概率确定变异池大小，在变异池中随机地挑出粒子进行变异操作，直到变异池中所有粒子完成变异。

为进一步验证算法的性能，将GAPSO 算法与CPSO（Chaos Particle Swarm Optimization）算法、PSO 算法对测试基准函数Sphere 进行仿真，仿真结果如图2 所示。

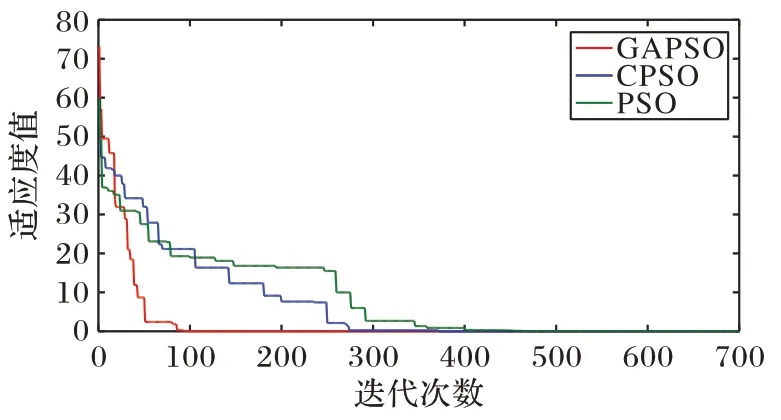
图2 不同算法的仿真结果Fig.2 Simulation results of different algorithms

从图2 分析可知，本文中所采用GAPSO 算法寻优结果以及收敛效果相较于CPSO 算法和PSO 算法更好，同时兼顾寻优速度快和收敛精度高等优点，改善了局部搜索能力。

2.3 算法优化步骤

1）获取初始信息：列车模型，线路信息，优化变量上下界vmax、vmin，种群的大小sizepop，学习因子c1、c2等参数。

2）粒子的初始化：随机产生N个满足条件的粒子作为初始种群，设定种群迭代次数maxgen，对种群粒子的位置及速度初始化操作。

3）计算初始种群的目标函数适应度值，记录种群的个体最优值pbest及其全局最优值gbest；

4）按照给定的杂交概率Pc，确定杂交池的大小，从杂交池中随机挑选出两个粒子进行杂交，使用式（11）～（12）进行位置和速度更新。

5）对杂交后新粒子的适应度值、全局最优、个体最优进行计算与更新。

6）按给定的变异概率Pm，确定变异池大小，在变异池中随机地挑出粒子根据式（17）进行变异操作，对变异后的粒子判断其是否满足要求。

7）对变异后产生的新粒子的适应度值、全局最优、个体最优进行计算与更新。

8）判断是否达到要求的停止迭代运算条件，如果达到，立即停止迭代运算并输出优化结果，程序结束；反之，返回步骤3）。

3 仿真实验与分析

3.1 仿真参数的设置

为了验证GAPSO 算法求解列车ATO 运行多目标优化问题的有效性，本文选择CRH3 车型结合武广客运专线某段线路进行仿真研究，列车性能参数和线路数据如表2～3和图3。

表2 仿真列车性能参数Tab.2 Performance parameters of simulated train

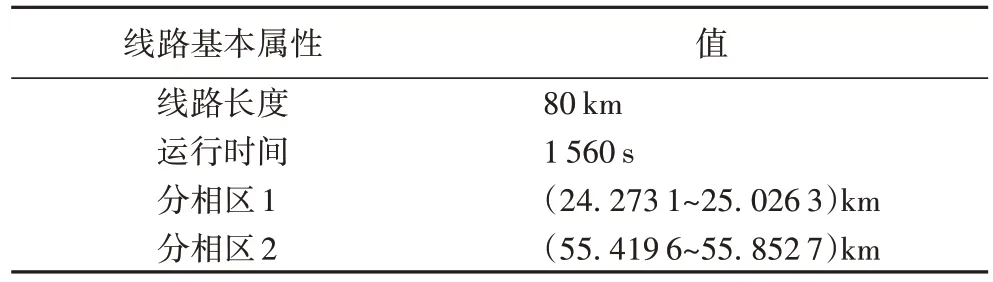
表3 仿真线路基本属性Tab.3 Basic attributes of simulated line

图3 仿真线路纵断面数据Fig.3 Simulated line vertical section data

由于线路中间有较大的限速值变化，在该路段需要采取制动操作来降低运行速度。因此，司机事先拟定9 个工况：牵引—惰行—制动—惰行—牵引—惰行—牵引—惰行—制动，将过分相区断电惰行纳入控制策略，采用GAPSO 算法对工况切换点处的速度进行寻优，得到一组满足ATO 运行多目标优化的速度值。种群数量为N=100，迭代次数maxgen=100，Pc=0.5，Pm=0.05。多目标优化的各个权重指标［18］分别为：ω1=0.180 0、ω2=0.378 6、ω3=0.167 1、ω4=0.274 3，事先求得最节能控制策略条件下Jmax=2.579 8、Emax=5.150 5*109。

3.2 实验结果及分析

在Matlab 仿真平台进行仿真，将GAPSO、CPSO、PSO 算法分别用于列车ATO 运行中的多目标优化，优化结果分析如下：

图4～5 为优化前的列车运行速度—距离曲线和运行工况序列，其中“1”表示牵引工况，“0”表示惰行工况，“-1”表示制动工况。根据图4～5 可知，列车以最小时分策略运行，即ATO 系统控制列车运行速度上下波动不超过2 km/h，通过工况切换以贴近线路的限定速度运行［19］。

图4 优化前的速度—距离曲线Fig.4 Speed-distance curve before optimization

图5 优化前的控制工况序列Fig.5 Sequence of control operating modes before optimization

图6～7 为不考虑分相区优化后的速度—距离曲线和运行工况序列，此时得到的最优工速况切换点速度分别为：277.33 km/h、253.71 km/h、197.36 km/h、157.60 km/h、284.05 km/h、261.83 km/h、290.12 km/h 和262.57 km/h。由图6～7 可知，优化以后降低了工况切换频率，同时增加了惰行距离，在缩短制动距离的情况下，充分利用列车的动能和势能，使得列车以较低能耗和较高舒适度的策略运行。

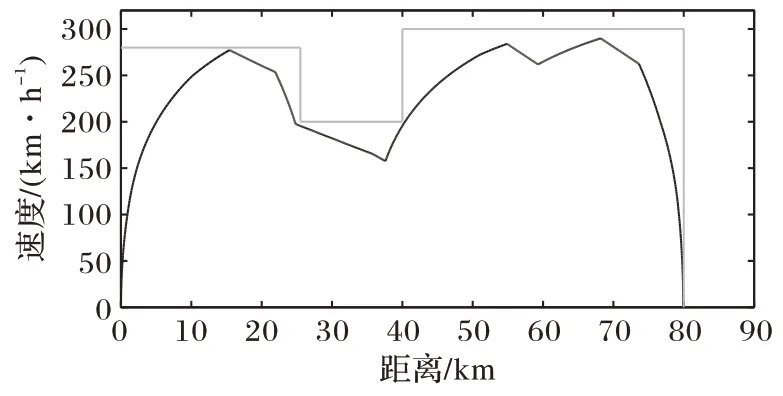
图6 不考虑分相区的优化后的速度—距离曲线Fig.6 Speed-distance curve without considering neutral zone after optimization

图7 不考虑分相区优化后的控制工况序列Fig.7 Sequence of control operating modes without considering neutral zone after optimization

将列车过分相断电惰行纳入控制策略以后，优化后的速度曲线和运行工况序列如图8～9 所示。此时得到的最优速度值分别为：277.09 km/h、253.25 km/h、196.51 km/h、157.55 km/h、253.81 km/h、236.98 km/h、289.18 km/h、246.06 km/h。由图8～9 可以看出，列车在经过分相区1 时，由制动工况转换为惰行工况，通过分相区后，继续制动至预定速度；在分相区2 区段内，采用惰行工况运行，驶出分相区继续牵引至预定速度。

图8 考虑分相区的优化后的速度—距离曲线Fig.8 Speed-distance curve of without considering neutral zone after optimization

优化后的结果对比分析如表4 所示。从表4 可知，优化前是以最小时分策略控制列车运行，此时运行能耗较大且舒适度较差。采用GAPSO 算法优化后，在不考虑分相区的情况下，总体运行时间增加了3.22%，误差低于计划运行时间的5%，保证了准时性要求；能耗降低了11.11%，舒适性提高了26.99%，停车误差降低了35.41%。考虑分相区带来的影响后，总体运行时间增加了4.01%，依旧满足准时性要求；能耗降低了13.29%，舒适度提高了26.62%，停车误差降低了21.62%。因此，GAPSO 算法的总体优化效果显著，在停车误差、运行时间、舒适度和能耗上均能体现。综上，优化后的目标速度曲线达到了综合最优的目的。