可解释性有序聚类方法及其应用分析
2022-03-01鲍君忠王利东
高 苏,鲍君忠,王 昕,王利东*
(1.大连海事大学理学院,辽宁大连 116026;2.大连海事大学航海学院,辽宁大连 116026)
0 引言
聚类作为机器学习领域典型的无监督学习方法,广泛应用于机器学习、模式识别、信息检索和数据挖掘[1-4]等领域。聚类根据“类间相似度低,类内相似度高”的原则,将一组数据分成一定数量的具有高度相似性的簇[5]。聚类方法的选择取决于数据类型、聚类目的和应用场合。为解决实际问题,目前已有多种聚类方法被提出,如基于划分的方法、基于密度的方法、层次聚类方法和模糊C均值(FuzzyC-Means,FCM)聚类方法[6-9]。
在决策领域中,决策者往往面对具有多个指标的任务,以簇为单元可帮助决策者了解和把握所研究样本的总体特征。决策中常常需要挖掘具有优势关系的有序簇,并且这些簇是未知的,通常把这种问题称为多指标有序聚类[10]。发达国家水平排序[11]、船舶分级管理[12]和分层次教学[13]等均涉及有序聚类问题。与传统的聚类方法不同,有序聚类方法不仅将样本划分到预定义的簇中,而且这些簇之间存在全序关系。有序聚类具有聚类和多指标决策的特征,不仅可以实现样本的等级划分,还可以为决策支持系统提供样本的等级分类管理。
针对中国海员职业幸福感指数评价的实际问题,本文构建了一种可解释性的有序聚类方法。该方法通过定义样本间优势度的计算公式,形成样本的优势度矩阵,结合K-modes聚类方法[14]和公理模糊集(Axiomatic Fuzzy Set,AFS)理论[15]确定样本的语义描述及最佳聚类数,并根据样本语义描述的模糊逻辑运算规则对等级划分结果赋予相应的语义解释。以海员职业幸福感指数的调查分析为研究样本进行分析,结果表明可以有针对性地分析不同等级中影响海员职业幸福感的因素,进而为改善海员工作环境、提高海员职业幸福感指数提供合理化建议。
1 相关工作
随着有序聚类在管理学领域的作用逐渐提升,如何有效解决等级划分问题引起了研究者的广泛关注。受偏好顺序结构评估法(Preference Ranking Organization Method for Enrichment Evaluation,PROMETHEE)的启发,文献[10]中提出了一种新的有序聚类方法,该方法基于样本间的不一致矩阵和两两偏好关系,在获得样本的整体优势度的基础上利用经典的聚类方法实现有序聚类。文献[16]中提出了一种结合K-Means 和PROMETHEE 的有序聚类方法。与上述方法相比,有序K-Means(OrderedK-Means,OKM)聚类方法具有更强的鲁棒性和一致性。为体现有序聚类问题中存在的不确定性,文献[17]中利用PROMETHEE 得到样本的综合优势度,然后在此基础上结合FCM 方法构建有序聚类方法OFCM(Ordered FCM)。上述方法实现了样本集的有序划分,一定程度上能够辅助人们进行不同领域实际问题的等级分析与管理。
为使聚类结果传递给人类更直观和易于理解的信息,对于多指标有序聚类问题,不仅仅要对样本集进行有序划分,而且也应提供相应的语义描述,这样才有利于辅助决策者做进一步决策,但上述方法在聚类结果的语义可解释性方面存在不足。本文构建了一种新的有序聚类方法,在聚类过程中考虑将每个指标值都直接参与有序聚类,并根据公理模糊集理论中简单概念的模糊逻辑运算结果对簇赋予语义解释,以此辅助决策者作出选择与表述。本文利用所构建的有序聚类方法对中国海员职业幸福感指数进行等级划分,然后结合当前社会对海员职业的认可度、海员对船上的工作压力承受程度以及海员的总体职业幸福感指数等指标[18]分析海员职业幸福感问题,且给出相应的建议。
2 预备知识
本章主要介绍有序聚类的定义、公理模糊集理论的相关概念和性质。
2.1 有序聚类
有序聚类的实质是利用已有的决策信息,采取特定的方法将有限个样本划分到相应的簇中,且簇之间存在全序关系。有序聚类的一般定义如下:
假设有n个样本,记为P={x1,x2,…,xn};m个属性,记为G={g1,g2,…,gm}。依据样本的属性值将n个样本划分到k个簇中,若满足以下3 个条件称其为有序聚类[10]:
1)P=;
2)∀i≠j,Ci∩Cj=∅;
3)C1≻C2≻…≻Ck。
其中:Ci表示第i个有序簇;≻表示优势关系,如果Ci≻Cj,则表示Ci中的样本优于Cj中的样本。
2.2 公理模糊集理论
公理模糊集(AFS)理论以AFS 代数和AFS 结构为基础[15],通过在数据集的相应属性(指标)上预设若干模糊简单概念(例如:小、中、大等),并将数据表中的记录信息转化成隶属函数及其模糊逻辑运算,从而产生具有可解释性且容易被人类理解和使用的样本描述与规则[15]。下面介绍与AFS 理论相关的定义和性质。
2.2.1 AFS代数
设数据集X上的模糊简单概念集合为M,根据文献[15]中所定义的模糊逻辑关系,对每一个模糊简单概念集合A⊆M,表示A中所有模糊简单概念的合取,表示的析取,即通过简单概念的逻辑运算得到的复杂概念,则所有复杂概念构成的集合可以表示为:

其中:I是任意一个非空指标集合。
定义1[19]设M是一个非空集合,EM*上的二元关系R定义如下:对于任意∈EM*,,∃Bh(h∈J),则Ai⊇Bh;2)∀Bj(j∈J),∃Ak(k∈I),则Bj⊇Ak。
2.2.2 AFS结构
假设X是论域,M是简单概念集合,三元组(M,τ,X)称为AFS 结构,其中τ是满足如下条件的映射τ:X×X→2M:
条件1:∀(x1,x2)∈X×X,τ(x1,x2)⊆τ(x1,x1);
条件2:∀(x1,x2),(x2,x3)∈X×X,τ(x1,x2)∩τ(x2,x3)⊆τ(x1,x3)。
τ被用来刻画X×X中样本序对和简单概念的对应关系,以此体现数据集的结构信息[15]。通常,τ采用如下形式[20]:
τ(x,y)={m|m∈M,x≥my}∈2M;(x,y)∈X×X
其中:≥m是简单概念m∈M上的序关系;x≥my表示x隶属于简单概念m的程度大于或者等于y隶属于简单概念m的程度,或者x≥my表示x在一定程度上隶属于简单概念m,而y完全不隶属于简单概念m。
利用AFS 结构,模糊概念η=∈EM的隶属函数定义[21]如下:

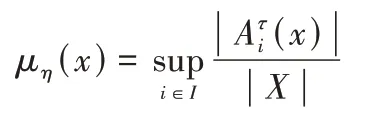
3 面向可解释性的有序聚类方法
为使得有序聚类结果具有良好的语义可解释性,以此对中国海员职业幸福感调研数据深入分析。本章结合AFS 理论设计基于模糊描述的有序聚类方法,该方法的流程如图1所示。

图1 面向可解释性的有序聚类方法流程Fig.1 Flowchart of ordered clustering method for interpretability
3.1 计算样本的优势度
隶属度能衡量样本属于模糊概念的程度,同时也可以提供不同样本在同一模糊概念下的差别程度。本文借鉴样本隶属度的求解方法[21]衡量样本在特定指标下的优势度。
定义2假设有n个样本P={x1,x2,…,xn},m个属性G={g1,g2,…,gm},对于∀xi∈P,则样本xi在指标gh(h=1,2,…,m)下的优势度定义如下:
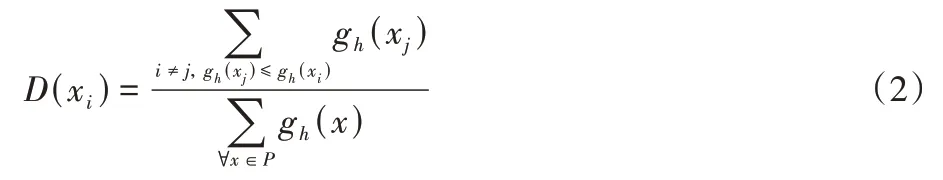
3.2 获得样本的模糊描述
当v=时,对于任意的样本xi,μv(xi)是样本xi属于模糊概念v∈EM的最大隶属度[21]。对于任意一个样本xi,确定最佳模糊描述的步骤如下。
1)令ε≥0,获取样本模糊描述的候选简单概念集合:


3)对于样本xi,选择最佳模糊描述:
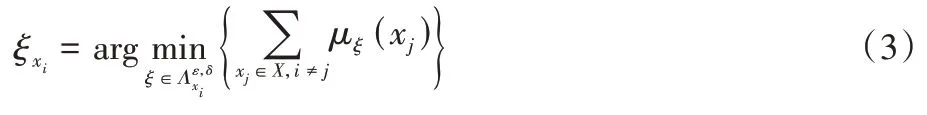
4)类Cj(j=1,2,…,k)的模糊描述表示为:

3.3 聚类过程及确定簇数
通过定义2 将原始的数据矩阵转化为优势度矩阵,并基于此利用K-modes 聚类方法对样本进行聚类,进而实现样本的等级划分。簇数作为聚类方法的输入参数,通常需要决策者事先指定。在有序聚类中,采用如下指标评价聚类结果的有效性[20]:

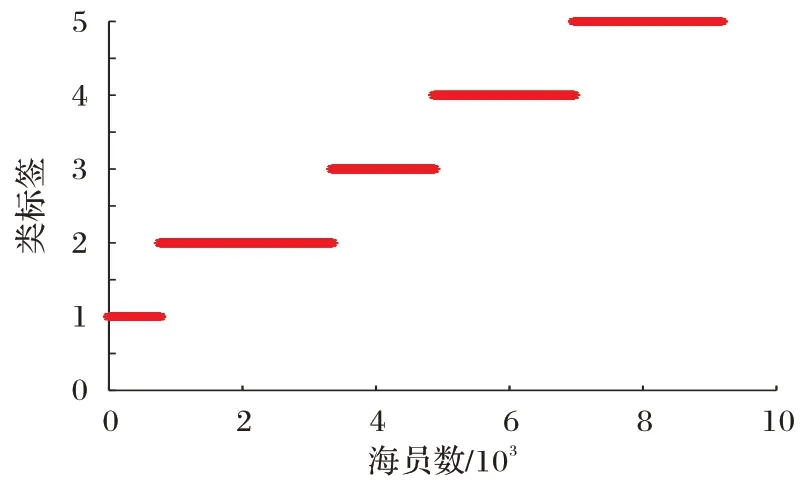
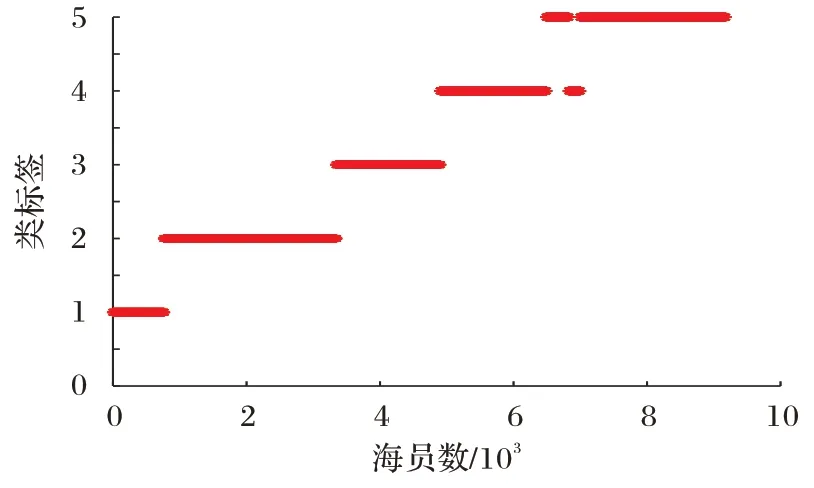
其中:Δh=,表示簇Ch(h=1,2,…,k)的类内紧凑度;δ(h,l)=D(rh)-D(rl),表示簇Cl(l=1,2,…,k;h 另一方面,从聚类结果的语义描述清晰性视角也可以确定类描述和目标聚类数。参照AFS 聚类方法中的有效性函数[22],聚类结果评价指标可以表示为: 由式(5)~(6)可知:评价指标Index取值越大表明聚类结果越好;评价指标I取值越小表明聚类结果的语义描述越清晰,此时得到的聚类数最佳。结合两个评价指标的优势,本文采用如下指标评价聚类结果: 当Dom取最大值时,可以得到最佳聚类结果。 本章利用所构建的决策方法对海员职业幸福感指数进行分析,以此得到不同幸福感指数等级群体及相应的语义描述,并为进一步改善海员工作环境、提高海员职业幸福感指数给出相应的建议。 步骤1 数据来源。 为切实了解海员的职业幸福感情况,真实反映影响我国海员职业幸福感的关键因素,大连海事大学研究团队联合信德海事网于2018 年4 月通过问卷调查的方式开展海员职业幸福感公益性调研工作[18]。本次调查问卷主要针对不同受教育程度、不同年龄段和不同职务的男性海员。海员通过5分制对这9 个指标下的调查结果进行打分,打分原则为:将“非常满意”“满意”“一般”“不满意”“非常不满意”分别赋予5 分、4 分、3 分、2 分、1 分,最终回收有效调查问卷为9 175份。依据这些调查数据,本文利用所构建的决策方法对海员职业幸福感指数进行等级分析。根据影响海员职业幸福感指数的重要程度[19],选取以下9 个具有代表性的指标:g1为海员对工资的满意情况;g2为海员对船上伙食的满意情况;g3为海员对船上业余活动的满意情况;g4为海员对船上实习生培训的满意情况;g5为海员对船上人际关系的满意情况;g6为海员对船上工作负荷的承受情况;g7为海员对现有社会保险的满意情况;g8为海员利用网络与外界联系的便利情况;g9为海员在船工作期间“下地休憩”便利程度。 步骤2 确定每个样本的最佳模糊描述。 根据AFS 结构的表示方法对打分数据矩阵建立AFS 结构(M,τ,X),其中M={mij|1≤i≤9,1≤j≤5}表示样本集X上与评价指标有关的简单概念集合,其中mij∈M表示在第i个指标下的第j个简单概念,j=1,2,3,4,5 对应的语义解释分别为:海员对第i个指标“非常不满意”“不满意”“一般”“满意”和“非常满意”。在取定参数δ=0.6,ε=0.05 情况下,利用式(3)得到每个样本的最佳模糊描述。 步骤3 聚类过程。 由式(2)计算每个指标下样本之间的优势度,将初始数据矩阵转化为优势度矩阵,进而使用K-modes 聚类方法得到有序簇。根据式(7),在不同聚类数k∈[2,10]下得到的评价指标值如表1 所示。 表1 不同k值下的评价指标值Tab.1 Evaluation index values under different k values 显然,当聚类数k=5 时,评价指标Dom取到最大值,此时聚类结果最佳,得到的有序聚类结果如图2 所示。 图2 有序聚类结果Fig.2 Ordered clustering results 从图2 可以看出,整个数据集样本分为5 个簇:C1、C2、C3、C4和C5,并且各自群体的职业幸福感指数有如下关系:C1≻C2≻C3≻C4≻C5。其中C1包含764 个样本,C2包含2 579 个样本,C3包含1 528 个样本,C4包含2 096 个样本,C5包含2 208 个样本。 步骤4 确定类描述。 根据预先设定的简单概念集合,及在参数取值δ=0.6,ε=0.05 情况下,利用式(3)得到每个样本的最佳模糊描述,并结合聚类结果由式(4)得到每一类的类描述。 第一类的类描述为: 即:海员对工资、船上伙食和船上业余活动非常满意;或者海员对船上工作负荷完全能承受,对实习生培训情况和船上人际关系非常满意;或者海员对利用船上网络与外界联系情况和在船工作期间“下地休憩”情况感到非常便利,对工资和现有社会保险非常满意,海员总体职业幸福感指数高。 第二类的类描述为: 即:海员对工资、船上伙食、船上业余活动、实习生培训情况和现有社会保险满意;或者海员对船上伙食和船上人际关系满意,对船上工作负荷能承受,对利用船上网络与外界联系情况和在船工作期间“下地休憩”情况感到便利,海员总体职业幸福感指数较高。 第三类的类描述为: 即:海员认为工资、船上伙食、船上业余活动、实习生培训情况、船上人际关系和现有社会保险一般,对船上工作负荷勉强能承受,对利用船上网络与外界联系情况和在船工作期间“下地休憩”情况感到一般,海员总体职业幸福感指数中等。 第四类的类描述为: 即:海员对工资、船上伙食、船上业余活动和实习生培训情况不满意;或者海员对工资、船上业余活动和船上人际关系不满意,对船上工作负荷不能承受;或者海员对现有社会保险不满意,利用船上网络与外界联系情况和在船工作期间“下地休憩”情况感到不便利;或者海员对工资、船上伙食、船上人际关系和现有社会保险不满意,对船上工作负荷不能承受,海员总体职业幸福感指数低。 第五类的类描述为: 即:海员对工资、船上伙食、船上业余活动和船上人际关系非常不满意,认为船上工作量超负荷;或者海员对工资、船上伙食、实习生培训情况以及现有社会保险非常不满意,对利用船上网络与外界联系情况和在船工作期间“下地休憩”情况感到非常不便利,海员总体职业幸福感指数非常低。 每个样本分别隶属于5 类模糊描述的隶属度如图3 所示,从图3 可以看出每类群体的语义描述相对清晰。 图3 样本集对于模糊描述的隶属度Fig.3 Membership degree of sample set to fuzzy description and 由我国国际航行海员职业幸福感指数的调查报告[18]可知,我国海员的职业幸福感指数与全球海员职业幸福感指数的同期水平差距较大。虽然调查报告真实地反映了影响我国海员职业幸福感的关键因素,但调查结果仅体现了目前海员的总体职业幸福状况和在每个指标下的加权平均分,并没有将海员根据不同的职业幸福感指数状况进行等级划分。本文通过面向可解释性的有序聚类方法,根据9 个评价指标不仅将9 175 名海员划分到不同幸福感指数等级群体中,而且还给出相应群体主要影响因素的语义描述,决策者可以根据不同指数等级所对应的语义描述进行分析并提出相应对策。由图2 可知,对于目前海员的总体职业幸福状况,满意人数约占这项调查活动总人数的1/3,并且通过第四类和第五类的类描述也可以看出,大多数海员对目前的总体职业幸福状况不满意。通过图3 可以看出,不同幸福感指数等级群体之间具有很好的区分度。根据有序聚类结果和调查问卷结果,可以发现海员的工作状况和生活环境有很多值得关注与改善之处: 1)在工资收入方面,国内海员劳务派遣薪酬管理制度存在其特殊性,导致国外船东提供给海员的工资与我国海员实际获得的工资之间存在较大的差异。因此,加强公司足额发放工资监管、海员个人所得税减免是提升海员职业幸福感的有效途径之一。 2)对于社会保险待遇,部分公司选择给海员缴纳最低档的保险,且出现保险缴纳地与公司所在地或与海员经常居住地不一致的情况,导致社会保险难以使用,职业挫败感强。因此需要建立适合海员职业特点的社会保险缴纳机制。 3)船上娱乐设施、设备配备参差不齐;船上业余活动较少导致海员之间缺乏交流,海员与家人的联系不便利易造成情绪压抑。为了改善上述状况,航运公司应该安装先进的通信设施,方便海员获取实时资讯以及与家人沟通;进而有利于海员平衡好家庭和工作。 4)对于海员在船工作期间下地休憩方面,船舶装卸效率高,港区离市场较远,某些港口缺乏“下地休憩”的便利服务,危化品作业港区管理部门不允许海员下地,船长安排海员下地休憩的意愿有时不强等因素导致下地困难。为了改善海员的休息状况,船长应积极安排海员下地休憩,有关部门推动下地休憩便利化。 为了说明面向可解释性的有序聚类方法对评价海员职业幸福感的可行性,将构建的方法与OKM 聚类方法[16]及OFCM 聚类方法[17]的聚类结果进行对比分析。针对海员职业幸福感评价问题,采用OKM 和OFCM 聚类方法对9 175 名海员进行聚类分析,结果如图4~5 所示。 图4 基于OKM聚类方法的聚类结果Fig.4 Clustering results based on OKM method 图5 基于OFCM聚类方法的聚类结果Fig.5 Clustering results based on OFCM method 上述两种方法是基于PROMETHEE 获取综合优势值基础上应用相应的聚类方法形成等级划分,没有充分体现多指标数据的结构与差异信息。本文应用文献[10]方法进行对比分析。当聚类数k=5 时,通过文献[10]方法分析海员职业幸福感指数评价问题,结果如图6 所示。 图6 文献[10]方法的聚类结果Fig.6 Clustering results using the method proposed in reference[10] 通过与OKM 聚类方法、OFCM 聚类方法以及文献[10]的方法进行对比分析,本文所构建的方法具有一定的合理性。该方法通过定义样本间优势度,结合聚类和模糊描述得到等级划分结果,不仅挖掘原始数据中的序关系,而且结合公理模糊集理论实现了等级划分结果的语义可解释性,以形成从定量到定性的辅助决策方法。 本文建立了面向可解释性的有序聚类方法,该方法不仅将样本划分到不同的等级,而且赋予每个等级集合相应的语义解释。本文将该方法应用于海员职业幸福感评价分析中,根据9 个评价指标对9 175 名海员进行等级划分,确定了5 个不同幸福等级群体。同时,根据不同等级群体的语义描述分析影响该群体幸福感指数的主要因素,并给出提升海员幸福感指数的建议。通过实例展示了所构建方法具有良好的应用性及可实践性,该方法的提出不但拓展了有序聚类方法,也为求解航运领域中大样本数据的实际决策问题提供了新的方法。

4 海员职业幸福感指数的实证分析
4.1 决策步骤


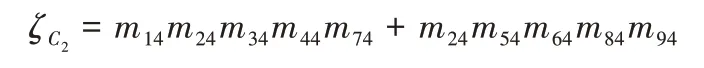




4.2 结果分析
4.3 对比实验分析


5 结语
