基于PSO-LSTM的电力负荷预测模型

0 引言

随着社会的高速发展，精准的短期电力负荷预测越来越重要。短期电力负荷的准确预测不仅对电网规划和电力系统安全经济运行有不可替代的作用，而且对减少发电成本、提高用电质量和市场规划等方面也有重要作用。短期电力负荷预测是指对未来几小时或几天的负荷进行预测。电力负荷的变化规律因受到气象、节假日等多种因素的影响，导致负荷的随机性和波动性较大，并且需要输入的模型参数较多，使用传统的预测方法难以胜任。

判决的那天，刑警队的几个警察来到贾鹏飞的关押地，向他出示了一张范峥峥的照片，问这是否是他的妻子，警察说她跳崖了。

在负荷预测方面，国内外的学者做了很多研究，传统方法有时间序列、自回归模型、神经网络、支持向量机等方法。张宗华等

提出的反向传播(BP)神经网络模型能够加快神经网络的收敛速度,同时提高预测精度

。艾欣

、李震

等将自回归积分滑动平均模型(ARIMA)应用于电力负荷预测。胡雨沙等

提出将粒子群优化算法(PSO)和最小二乘支持向量机(LSSVM)相结合的短期电力负荷预测方法(PSO-LSSVM)。魏明奎等

提出了基于PSO优化的自组织特征映射网络(SOFM)和遗传算法(GA)优化的LSSVM的短期电力负荷预测方法

。虽然这些方法能够解决非线性的问题，但是在处理时间序列的时候容易出现问题，并且在预测随机性较大的负荷时精度比较低。

随着深度学习的出现，很多学者把目光转向了深度置信网络、卷积神经网络、循环神经网络等。孔祥玉等

充分利用深层架构的特征提取优势，提出了一种采用深度学习的暂态稳定评估方法。王刚等

提出了基于深度学习与权值共享机理的负荷预测方法，该方法有效提高了工业园区负荷预测的精度。王文卿等

提出了一种自编码器与粒子群优化算法优化卷积神经网络的短期负荷预测模型，用自编码器对卷积神经网络的输入数据进行处理，通过PSO算法对卷积神经网络进行优化，提高了预测精度。深度学习在大量数据的预测方面有着明显的优势，但是在处理时间序列预测的时候容易出现梯度爆炸的问题，导致预测的精度下降。

针对梯度问题，有学者提出了长短期记忆(LSTM)算法来解决梯度爆炸。N Neeraj等

提出了一个新的模型——奇异谱分析-长短时记忆(SSA-LSTM)来解决观测数据的不规则和噪声特性问题。Tan M等

提出了一种基于LSTM网络的混合集成学习预测模型，将其用于超短期工业电力需求预测。LSTM是一种神经网络算法，其超参数大多依靠经验选择，不仅耗时，而且所选择的超参数可能不是最优，从而导致预测结果不理想。本文采用PSO算法对LSTM的超参数进行寻优，训练模型，找到合适的超参数，并进行验证。

作为公路管理站桥梁工程师，王世君负责对全县省道及县道上的桥梁状况作经常检查及定期检查，工作条件非常艰苦，常常顶寒风、冒酷暑，精心检测，发现病害及时处理、上报，在他的任职期间，未发生一起因桥梁问题导致的责任事故。

同时抓住平山西柏坡这一红色革命圣地特点，指导平山县图书馆加强文献采访工作，尤其是与平山、西柏坡有关的红色文献的征集与服务。为其提供省地方文献查询和燕赵红色记忆馆文献目录查询，并指导其多途径检索国家中心书目中心数据，丰富采访信息来源渠道。

1 LSTM神经网络算法

LSTM作为RNN的一种特殊形式，为了解决RNN梯度 爆 炸的问题

，首先由Hochreiter等 在1997年提出，如今在时间序列数据的预测应用十分广泛。

1.1 LSTM网络结构参数

德国ETAS（易特驰）集团为客户提供用于汽车电控单元（ECU）开发和维护的各种集成工具和解决方案。作为一流的工具供应商，易特驰始终提供创新、高质量的产品，并针对ECU生命周期的各个阶段提供解决方案。该公司2005年进入中国，为中国本土客户提供全方位的服务以及个性化的解决方案。

LSTM的结构如图1所示，与普通的RNN相比，LSTM的结构更加复杂，它将RNN中每个神经元的单层网格换成了四层网格。图中的σ和tanh分别代表Sigmoid函数和Tanh函数，起到闸门的作用，它们决定着上一时刻的负荷信息向前传递时所占的比重。激活函数的值越接近1，上一时刻的负荷信息向前传递得越多；激活函数越接近0，上一时刻的负荷信息向前传递越少。

LSTM网络主要由三个门控单元控制，细胞状态C

相当于信息传输的路径，通过Sigmoid函数和Tanh函数控制当前输入的电力信息和细胞记忆中电力信息的选择与丢弃。在t时刻，细胞单元（当前神经元）的输入包括当前时刻输入变量X

、前一时刻隐藏层状态变量h

和前一时刻细胞单元状态变量C

。依次经过f

、i

和o

之后，细胞单元的输出包括当前时刻输出变量h

和当前时刻细胞单元状态变量C

。

俗话说“授人以鱼不如授人以渔”，教师在阅读教学中应该注重讲解分析过程而不是分析结果，只有让学生学会分析文章，学生在课外进行自主阅读水平才能得以提升。因此，教师在教学时为了让学生理解分析过程，在课堂中学会自主分析，可以通过任务驱动法帮助学生进行理解。在讲解文章时，教师可以先让学生进行自主思考，将课堂交给学生，为了督促学生自主学习，教师可以设计几个问题。在学生自主思考之后便通过师生互动环节了解学生的自主学习情况。最后根据学生的反馈信息调整教学过程，对阅读技巧进行针对性讲解，帮助学生查漏补缺。通过这样的方式可以提高课堂教学效率并且促进学生思维能力的发展，提高学生的自主学习能力。

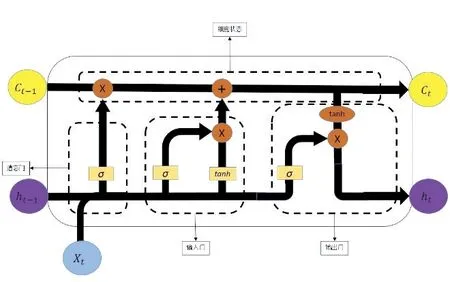
各个门控单元通过计算初始权重和偏置矩阵得到它们所需负荷信息的占比，再根据损失函数调整得到最优的权重矩阵和偏置矩阵，得到最终的负荷信息占比。

1.2 LSTM超参数

神经网络模型在网络结构参数之外，还包括大量的超参数（hyper-parameters）。超参数是指模型在开始训练之前设定的参数，训练过程中始终保持不变。通常情况下，根据模型结果调整超参数，获得一组最优超参数，提高模型的效果和性能。

为了分析LSTM算法的性能，本文采用北京市某区的居民生活用电以及工业用电等总电力负荷作为数据样本，记录了每天24小时的实际电力消耗。本文选取2017年第一季度的数据作为样本数据，对原始数据进行异常数据处理和归一化处理。一方面对不合理数值或者空值采用平均值代替；另一方面，为了消除数值差异过大的问题，采用最大最小归一化方法使其处于同一数量级。

2 PSO-LSTM负荷预测模型

2.1 PSO算法

5)比较粒子的适应度值。寻找个体最优位置和全局最优位置，更新最优的适应度值。

PSO算法是模拟大自然鸟群觅食行为得出的一种全局寻优算法。将全局中的每一个可能都看作一个粒子，每个粒子都有不同的运动方向和速度，朝着最优位置前进。通过更新个体最优位置和全局最优位置，得到目标函数的最优解，从而实现全局寻优

。本文把PSO与LSTM算法相结合，构建了PSO-LSTM预测模型。

网络仿真场景中，数据中继卫星为1颗GEO卫星，用户卫星包括N=6,12,18颗轨道高度为300km的LEO卫星三种情况.其中，三种不同LEO用户卫星数量情况下，LEO用户卫星的升交点赤经(Right Ascension of Ascending Node，RAAN)依次分别间隔5°，10°和15°.为分析方便，其余轨道参数均设置为0.设用户卫星数据帧产生时间服从泊松分布.根据第三节的分析，选取时隙大小为0.28s，具体参数如表1所示.

2.2 PSO-LSTM负荷预测模型

本文将PSO与LSTM神经网络结合的方法是把LSTM的三个关键超参数（神经元数量L

，学习率ε和训练迭代次数k）作为PSO粒子的寻优变量，通过更新粒子的速度和位置，从而使负荷预测的适应度值达到最低，获得更优的模型参数。PSO优化LSTM模型参数的流程图如图2所示。

1)预处理电力负荷历史数据。剔除其中有明显偏差和有问题的数据，将数据进行归一化，缩放到同一区间。

2)建立LSTM模型。确定需要寻优的参数，神经元数量L

，学习率ε和训练迭代次数k，并确定它们各自寻优的范围。

3)初始化PSO参数。包括粒子的初始速度和位置，学习权重，训练次数和规模等。

将LSTM的3个超参数作为PSO的待优化参数，适应度函数设置为

由于电力负荷的历史数据是一个时间序列数据，LSTM模型在时间序列的分析中表现优异。而LSTM算法中的超参数对负荷预测的准确性有很大的影响。本文用PSO对LSTM的超参数进行寻优，并在负荷预测时更新其相应的数值。

在本研究中，我们以高表达her-2的NCI-N87胃癌细胞株为研究对象，通过研究不同浓度的槐耳清膏在处理细胞不同时间后，对NCI-N87细胞增殖、凋亡及相关自噬蛋白表达的影响。

6)判断是否达到最大迭代次数。如果达到最大迭代次数，将得到的最优参数传给LSTM模型，并进行训练和预测。若未达到要求，则返回步骤(5)。

3 电力负荷预测

3.1 电力负荷数据预处理

常见的超参数包括学习率、训练次数、神经元个数、输出维度等。其中，学习率表示梯度下降算法中的步长，如果学习率过高会导致网络震荡，找不到最优结果，学习率太小会导致学习的时间增加，学习率的大小一般在0.01~0.001之间进行调整。其次，训练次数是通过学习率来调整网络权重的次数，训练次数少会得不到理想的效果，训练次数过多会造成资源的浪费。在本文中需要调节的超参数包括神经元数量L

，学习率ε和训练次数k。

设X

和X

分别是指标X的最小值和最大值，最大最小归一化是将X的每一个原始值x通过线性化的方法变换为区间[0,1]的值x

，如式(1)：

从处理完的数据中选择2017年1月1日到2017年3月30日的数据用作训练集，训练获得最优超参数；使用3月31日的数据作为测试集，验证预测结果的有效性。

网络结构参数，是在训练过程中通过损失函数反馈后进行调整的参数。在LSTM网络中需要调整的网络结构参数，即权重矩阵和偏置矩阵，主要存在于遗忘门f

、输入门i

和输出门o

三个门控单元中。

3.2 PSO-LSTM负荷预测模型

4)确定粒子的适应度函数。本文将预测模型的MAPE值作为粒子的适应度函数，寻找最优模型参数。

其中平均绝对百分比误差（MAPE）是指用电量真实值和预测值之间的百分比误差的平均值：

谈到与拍摄对象建立的关系时，Réhahn绝对是身体力行的摄影师，他和当地许多人成为了朋友，甚至“亲如一家”。他会定期造访，或邀请人们到家中做客。作为工作的一部分，他在靠近老挝边境的越南西江地区为戈都族建造了一座文化博物馆，所用资金全部来自他在画廊的销售所得。他还资助了当地几个儿童的教育，并为居民支付医疗保健费用，或者购买船只、自行车、奶牛或照相机来帮助人们谋生。

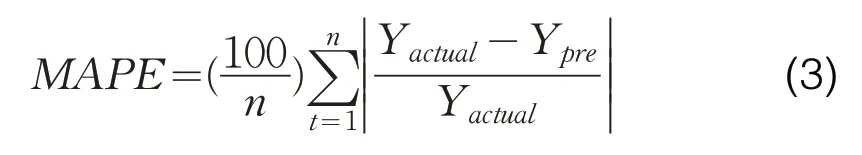
式（3）中，Y

代表负荷的实际值，Y

代表负荷的预测值，n表示预测负荷点的个数。同时，设置种群规模为20个，最大迭代次数设50次，学习因子c

=2，c

=2。LSTM超参数的设置范围如表1所示。

式中，Fj为水资源承载力指数，Fj＞1表示实际承载的农业经济规模大于水资源可承载的最大农业经济规模，表现为水资源超载；Fj=1，表示实际农业经济规模等于最大可承载农业经济规模，水资源承载平衡；Fj＜1，表示实际承载的农业经济规模小于水资源可承载的最大农业经济规模，水资源承载力有盈余。

寻优过程中得到的适应度和超参数变化曲线图如图3所示。从图3(a)可以看出，适应度曲线在迭代9次趋于稳定，可以得到最优的超参数。从图3(b)中可以看出在寻找最优神经元数量的过程中只有一次波动，最优的神经元个数为265。从图3(c)中可以看出前期在寻优过程中经过两次波动，最终得到的学习率为0.0063。从图3(d)中可以看出训练次数的寻优过程相对简单，结果为823。

3.3 负荷预测结果分析

为了直观地比较PSO-LSTM与传统的LSTM和BP神经网络预测方法的准确程度，将这三种方法对未来一天的预测值和真实值结果进行比较，如图4所示。

从图4中比较可以看出，负荷曲线包括两峰两谷：在凌晨00:00-6:00，负荷到达第一个低谷，经过一夜的休整，新的一天开始，对电负荷的需求开始增加；在中午12:00左右，用电量达到一天中的第一个峰值，此时是大部分人中午用餐或者休息的时间，居民或者是工厂用电都进入了短暂的休息期，对电负荷的需求量开始降低；在下午14:00左右，用电量到达第二个低谷，此时短暂的休息时间结束，大部分人继续工作，对电负荷的需求变大；到晚上22:00左右，用电量达到了第二个峰值，这时大部分人已经下班，或者开始休息，对电负荷的需求开始减少。由图4可见，三种方法都可以预测负荷的变化趋势，但是在上午、中午和晚上等用电量转折点的时候，本方法预测的精度更高一些，能预测出电负荷变化的趋势，并且与真实数据的峰谷值更加接近。BP神经网络法和LSTM方法预测的负荷值虽然与真实数据相差不大，但是，在峰谷值的时候预测的精度低于本文方法的准确度。

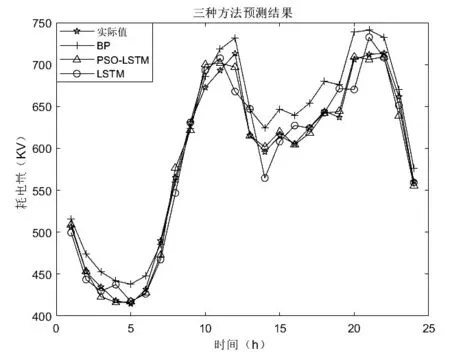
为了进一步评估所提模型的预测性能，本文把三种方法的平均绝对百分误差(MAPE)和均方根误差(RMSE)作为参考指标，其中MAPE如式（3）所示，RMSE指标的计算如式（4）所示：

式中，Y

代表负荷的实际值，Y

代表预测的负荷值，n表示预测负荷点的个数。

所预测结果的MAPE和RMSE越小，证明所提出的预测方法越好。三种方法预测的MAPE和RMSE如表2所示。

从表2数据可以更加直观地看出三种方法的预测准确性。预测精度从高到低分别为PSO-LSTM、LSTM、BP，表明经过PSO优化的LSTM模型的预测值和真实值之间的差值最小。PSO-LSTM的MAPE值为1.73%，RMSE值为12.17，相比于BP神经网络方法，MAPE的值降低了1.67%，RMSE的值降低了17.95，说明PSO-LSTM的预测值和真实值更加接近，能提高负荷预测的精度；相比于LSTM方法，MAPE值降低了0.64%，RMSE值降低了11.93，说明PSO算法可以提高LSTM对超参数的寻优能力，模型的预测性能明显提升。

4 结论

针对电力负荷预测问题，本文提出PSO-LSTM模型对电力负荷进行预测。利用PSO算法可以有效寻找全局最优解的特点对LSTM网络的超参数进行优化，可以避免人为选择参数造成的LSTM模型参数不是最优的问题，减少人为因素对模型精度的影响。在负荷预测的时候，对电力负荷进行实时更新，能够及时调整LSTM网络结构参数的权重。从仿真结果可以得出，与BP神经网络和传统的LSTM神经网络相比，基于PSO优化的LSTM模型能够明显提高短期负荷预测的精确度和准确性。使用北京市某区的电力负荷的数据对所提出模型进行检验，得出本文模型的平均绝对误差百分比为1.73%，小于2%，证明了本文方法的有效性和实用性。

[1]张宗华，赵京湘，卢享，等.基于遗传算法的BP神经网络在电力负载预测中的应用[J].计算机工程，2017，43(10):277-282+288.

[2]艾欣，周志宇，魏妍萍，等.基于自回归积分滑动平均模型的可转移负荷竞价策略[J].电力系统自动化，2017，41(20):26-31+104.

[3]李震，张思，任娴婷，等.基于数据驱动的线性聚类ARIMA长期电力负荷预测[J].科学技术与工程，2020，20(16):6497-6504.

[4]胡雨沙，李继庚，洪蒙纳，等.基于PSO-LSSVM算法的造纸过程短期电力负荷预测模型[J].中国造纸学报，2019，34(1):50-54.

[5]魏明奎，叶葳，沈靖，等.基于自组织特征神经网络和最小二乘支持向量机的短期电力负荷预测方法[J].现代电力，2021，38(1):17-23.

[6]孔祥玉，郑锋，鄂志君，等.基于深度信念网络的短期负荷预测方法[J].电力系统自动化，2018，42(5):133-139.

[7]王刚，杨晓静，张志军，等.基于深度神经网络与权值共享的工业园区负荷预测.电测与仪表，2021，58(1):137-141.

[8]王文卿，撖奥洋，于立涛，等.自编码器与PSOA-CNN结合的短期负荷预测模型[J].山东大学学报(理学版)，2019，54(7):50-56.

[9]N Neeraj，Mathew J，Agarwal M，et al.Long short-term memory-singular spectrum analysis-based model for electric load forecasting[J].Electrical Engineering，2020(1):1-16.

[10]Tan M，Yuan S，Li S，et al.Ultra-Short-Term Industrial Power Demand Forecasting Using LSTM Based Hybrid Ensemble Learning[J].IEEE Transactions on Power Systems，2020，35(4):2937-2948.

[11]Hochreiter S，Schmidhuber J.Long Short-Term Memory[J].Neural Computation，1997，9(8):1735-1780.

[12]宋刚，张云峰，包芳勋，等.基于粒子群优化LSTM的股票预测模型[J].北京航空航天大学学报，2019，45(12):2533-2542.