有序思考数图形

黄旭军

阿木老师刚进教室，就看到班里四大“调皮王”站在前面。原来，他们推来推去，撞到了花盆，花盆倒地摔成了八块。“我们真不是故意的，我们愿受罚！”四个“调皮王”诚恳地说。

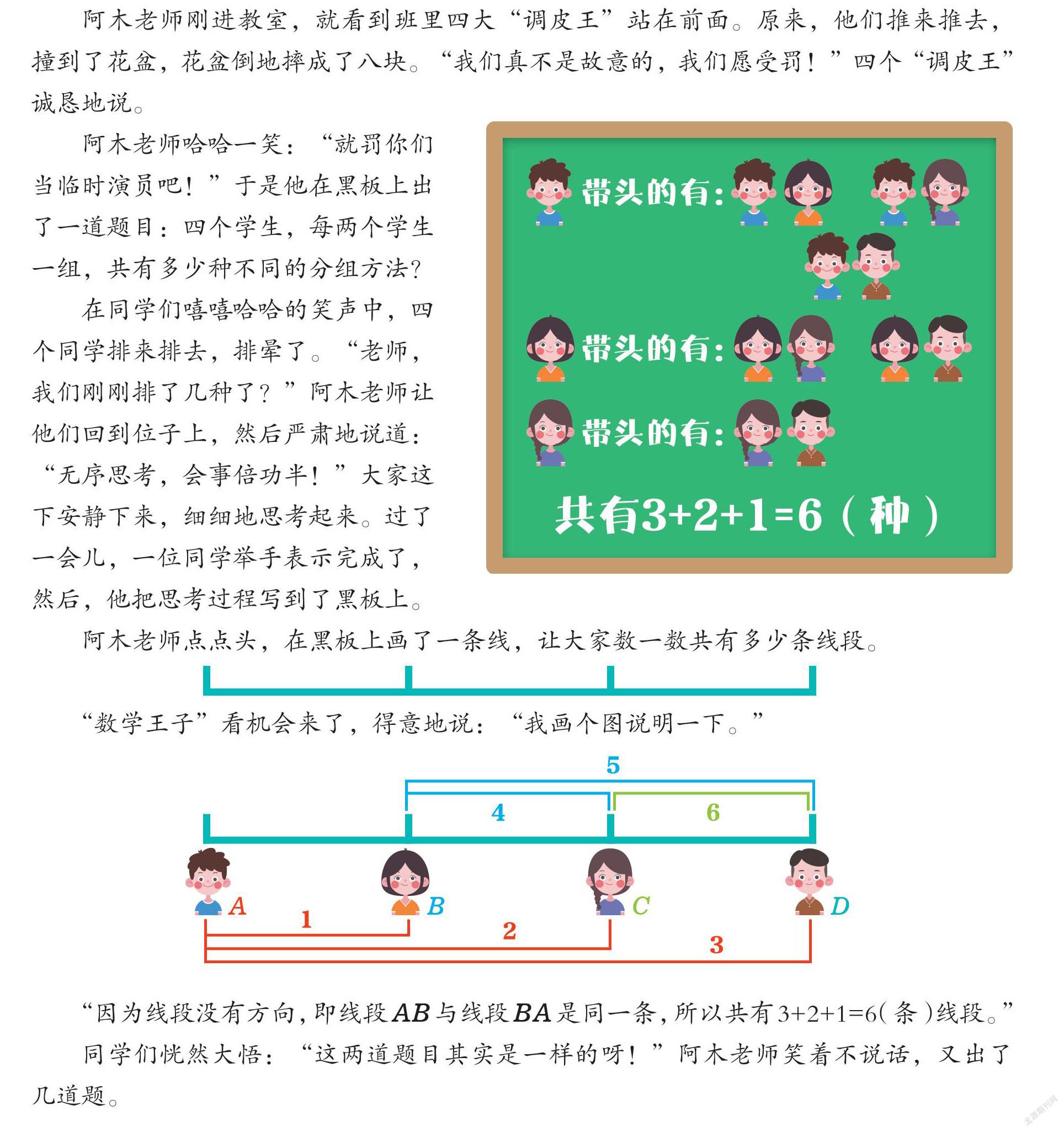
阿木老师哈哈一笑：“就罚你们当临时演员吧！”于是他在黑板上出了一道题目：四个学生，每两个学生一组，共有多少种不同的分组方法？

在同学们嘻嘻哈哈的笑声中，四个同学排来排去，排晕了。“老师，我们刚刚排了几种了？”阿木老师让他们回到位子上，然后严肃地说道：“无序思考，会事倍功半！”大家这下安静下来，细细地思考起来。过了一会儿，一位同学举手表示完成了，然后，他把思考过程写到了黑板上。

阿木老师点点头，在黑板上画了一条线，让大家数一数共有多少条线段。

“数学王子”看机會来了，得意地说：“我画个图说明一下。”

“因为线段没有方向，即线段AB与线段BA是同一条，所以共有3+2+1=6（条）线段。”

同学们恍然大悟：“这两道题目其实是一样的呀！”阿木老师笑着不说话，又出了几道题。

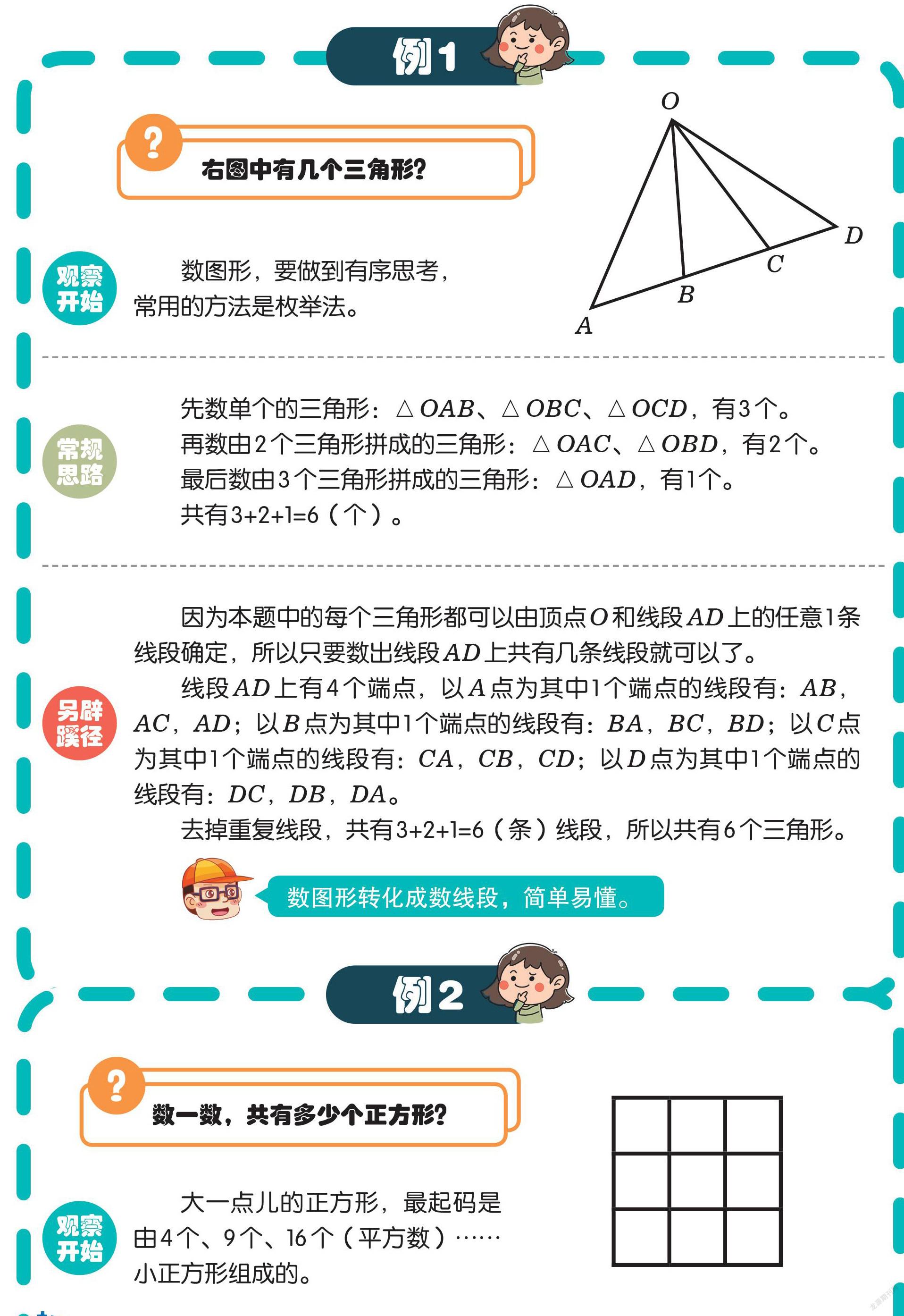
右图中有几个三角形？

数图形，要做到有序思考，常用的方法是枚举法。

先数单个的三角形：△OAB、△OBC、△OCD，有3个。

再数由2个三角形拼成的三角形：△OAC、△OBD，有2个。

最后数由3个三角形拼成的三角形：△OAD，有1个。

共有3+2+1=6（个）。

因为本题中的每个三角形都可以由顶点O和线段AD上的任意1条线段确定，所以只要数出线段AD上共有几条线段就可以了。

线段AD上有4个端点，以A点为其中1个端点的线段有：AB，AC，AD;以B点为其中1个端点的线段有：BA，BC，BD;以C点为其中1个端点的线段有：CA，CB，CD;以D点为其中1个端点的线段有：DC，DB，DA。

去掉重复线段，共有3+2+1=6（条）线段，所以共有6个三角形。

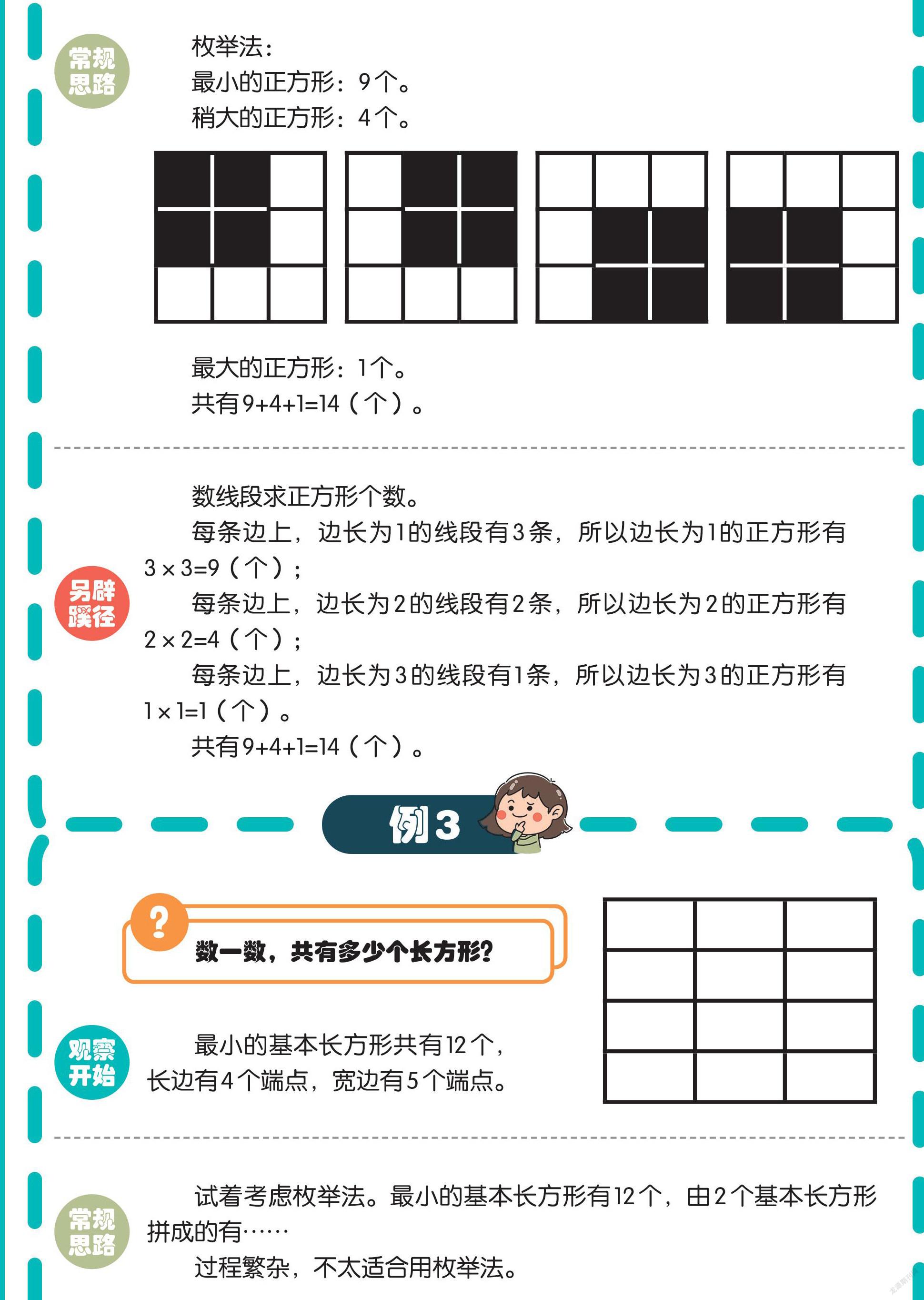
大一点儿的正方形，最起码是由4个、9个、16个（平方数）……小正方形组成的。

枚举法：

最小的正方形：9个。

稍大的正方形：4个。

最大的正方形：1个。

共有9+4+1=14（个）。

数线段求正方形个数。

每条边上，边长为1的线段有3条，所以边长为1的正方形有3×3=9（个）;

每条边上，边长为2的线段有2条，所以边长为2的正方形有2×2=4（个）;

每条边上，边长为3的线段有1条，所以边长为3的正方形有1×1=1（个）。

共有9+4+1=14（个）。

最小的基本长方形共有12个，长边有4个端点，宽边有5个端点。

试着考虑枚举法。最小的基本长方形有12个，由2个基本长方形拼成的有……

过程繁杂，不太适合用枚举法。

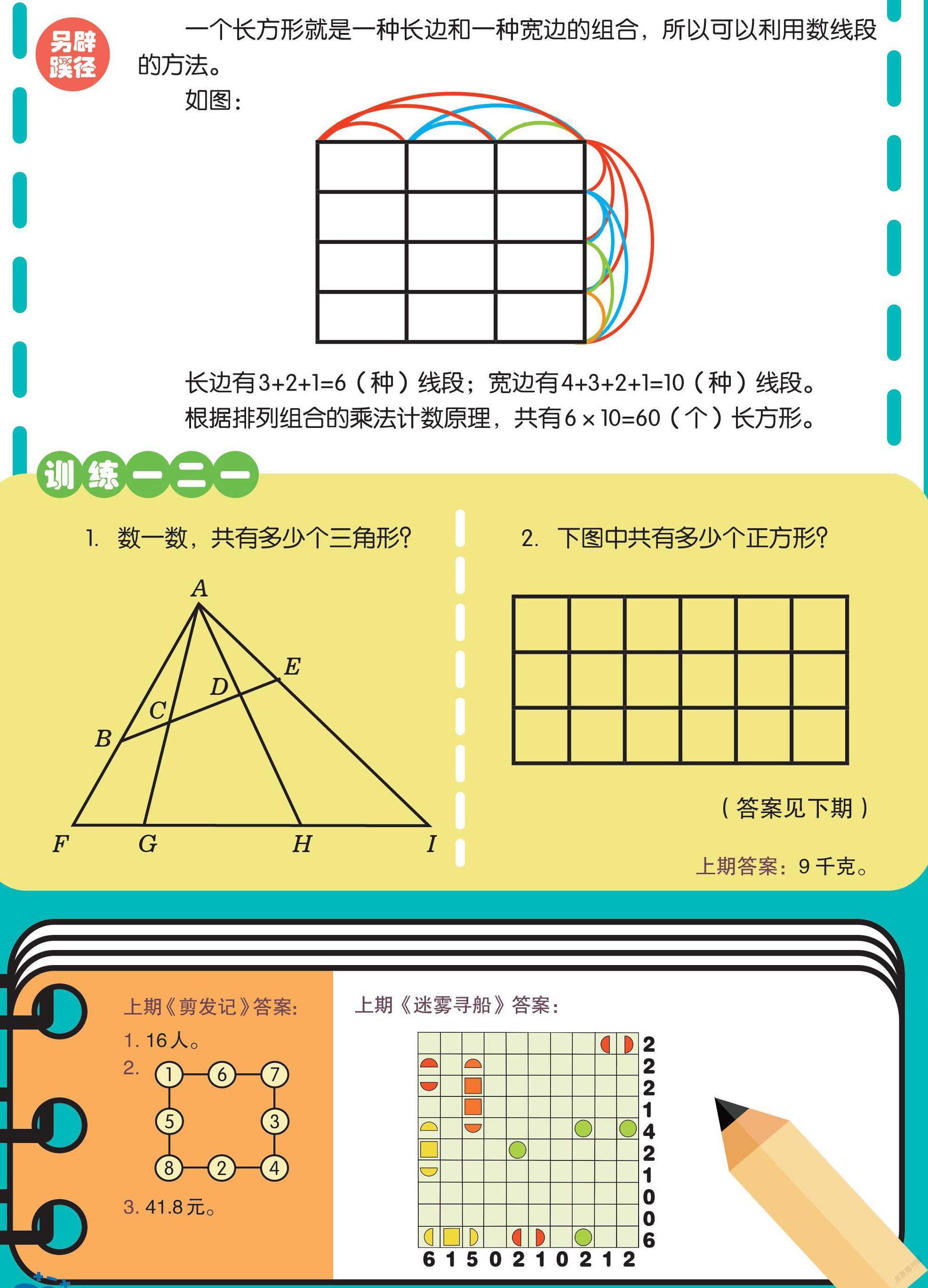
一个长方形就是一种长边和一种宽边的组合，所以可以利用数线段的方法。

如图：

长边有3+2+1=6（种）线段;宽边有4+3+2+1=10（种）线段。

根据排列组合的乘法计数原理，共有6×10=60（个）长方形。