地平线有多远？

捌元

站在帆船上眺望大海的时候，我们会看到远处的海面与天空汇成了一条线，那便是海平线。而当我们站在平原上极目远眺的时候，看到远方的地面与天空匯成的一条线，便是地平线。

当我们身处没有任何建筑物遮挡的平原时，会发现地平线离我们很近;当我们坐在飞机上看向远处的时候，又发现地平线离我们很远。这是为什么呢？难道是地平线在跟我们玩捉迷藏吗？

地平线的距离

其实，当我们站在平原上极目四望的时候，我们在大地上的视野范围是一个很大的平面圆，半径在5千米左右。所以，朝着同一个方向观察的时候，我们就会看到地平线。

地平线与我们的距离取决于我们所处的高度。当我们站在平原上，不考虑光线折射等因素时，地平线离我们大约只有5千米。如果一个人以1.2米/秒的速度行走，那么大概需要70分钟就可以走完这5千米。这么看来，5千米也不是很远吧。

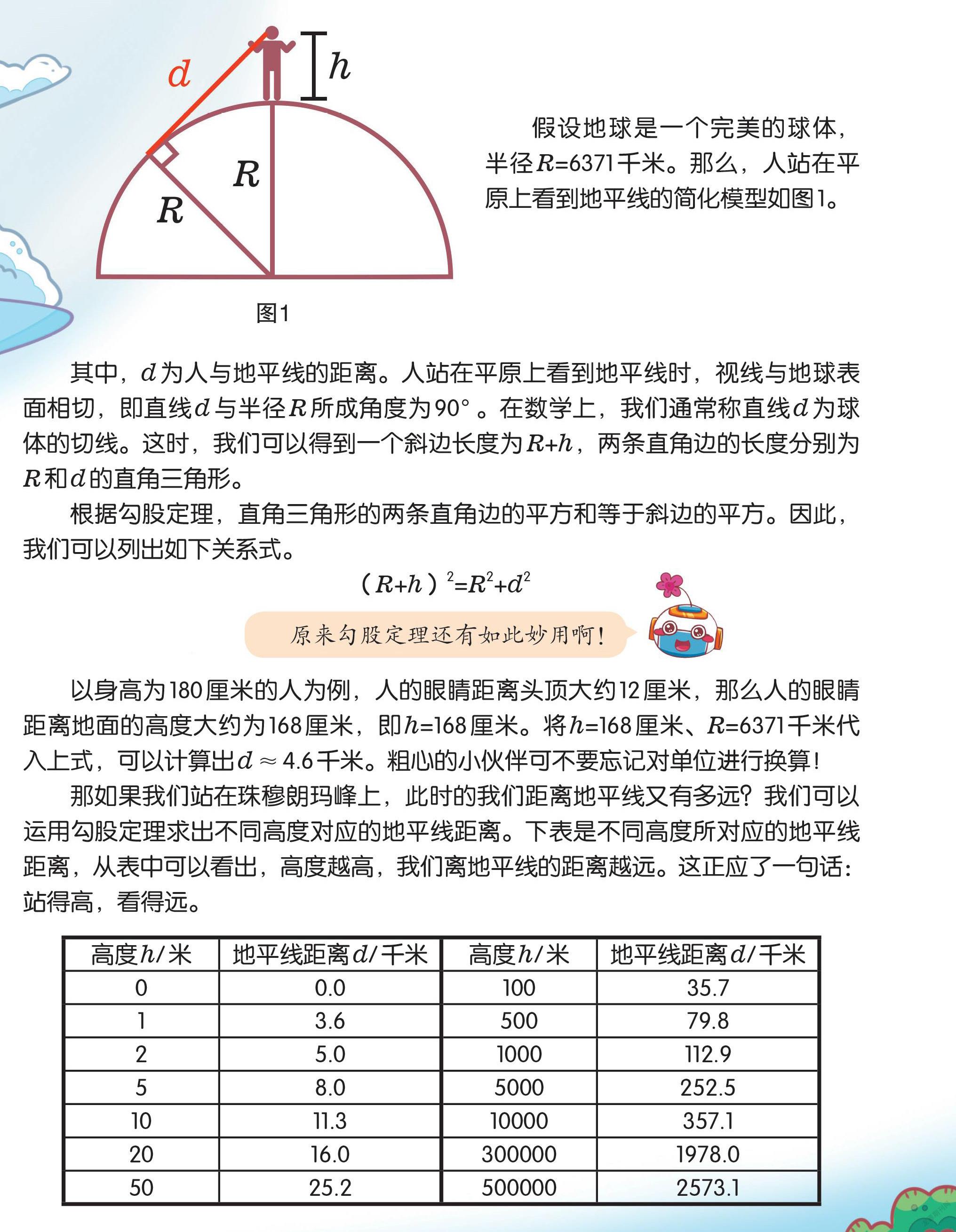
其中，d为人与地平线的距离。人站在平原上看到地平线时，视线与地球表面相切，即直线d与半径R所成角度为90°。在数学上，我们通常称直线d为球体的切线。这时，我们可以得到一个斜边长度为R+h，两条直角边的长度分别为R和d的直角三角形。

根据勾股定理，直角三角形的两条直角边的平方和等于斜边的平方。因此，我们可以列出如下关系式。

（R+h）2=R2+d2

以身高为180厘米的人为例，人的眼睛距离头顶大约12厘米，那么人的眼睛距离地面的高度大约为168厘米，即h=168厘米。将h=168厘米、R=6371千米代入上式，可以计算出d≈4.6千米。粗心的小伙伴可不要忘记对单位进行换算！

那如果我们站在珠穆朗玛峰上，此时的我们距离地平线又有多远？我们可以运用勾股定理求出不同高度对应的地平线距离。下表是不同高度所对应的地平线距离，从表中可以看出，高度越高，我们离地平线的距离越远。这正应了一句话：站得高，看得远。

假设地球是一个完美的球体，半径R=6371千米。那么，人站在平原上看到地平线的简化模型如图1。

原来勾股定理还有如此妙用啊！

月球上的地平线

有的同学会思考，既然可以计算我们与地球上地平线的距离，那么是否可以计算我们与月球上地平线的距离呢？这当然是可以的！

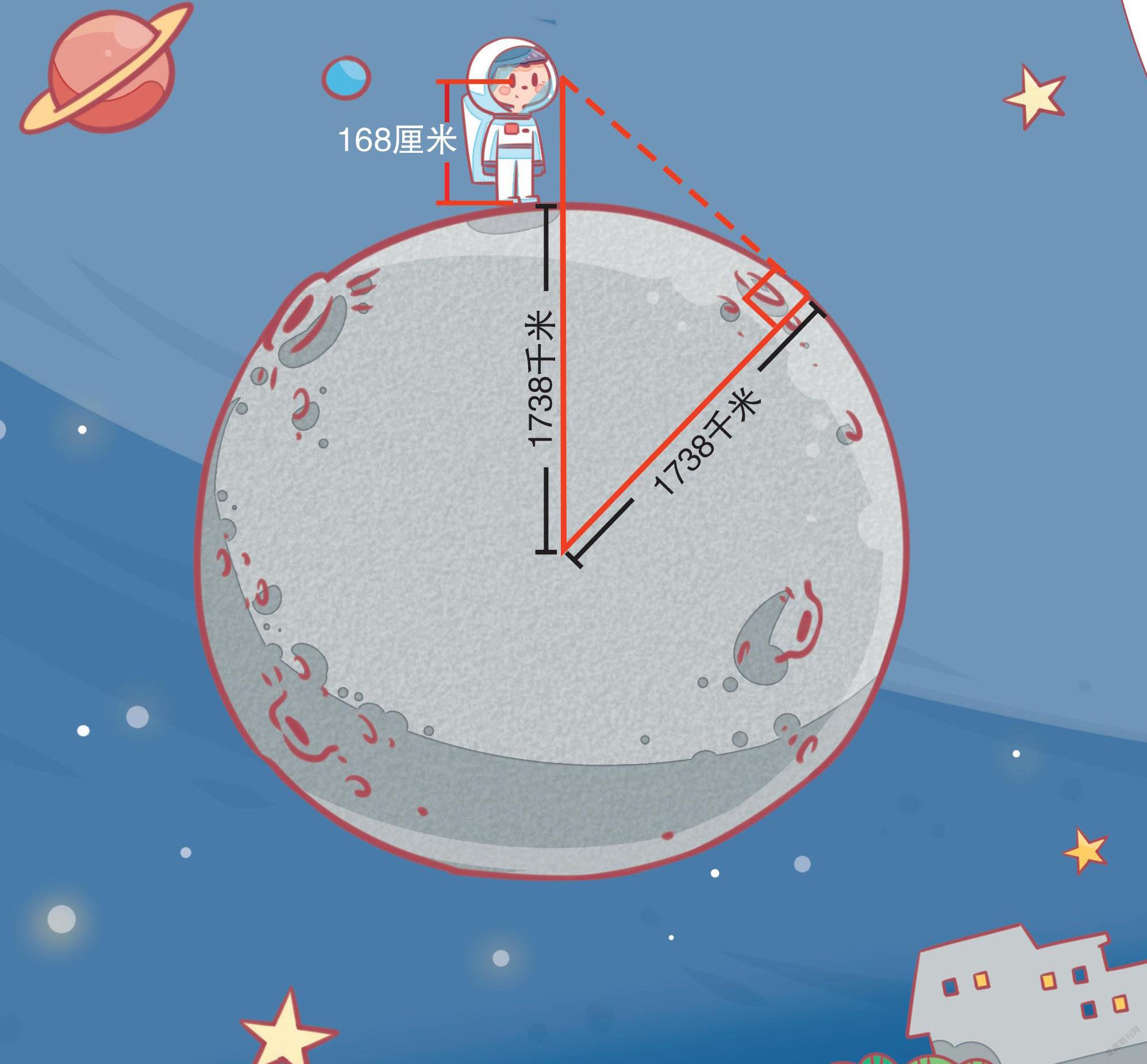
假设月球是个完美的球体，上面没有任何高山和高大的建筑物，半径R=1738千米。如果你站在月球上，你的眼睛距离月球表面的高度仍然是168厘米，那么你在月球上与地平线的距离大约为2.4千米，这个距离只有我们与地球上地平线的距离的一半左右。

地平线上的错觉

地球上地平线的距离都是以地球为参照物来计算的。如果换个参照物来思考，你会不会发现一些有趣的现象呢？接下来，我们将以月亮为参照物，看看月亮和地平线组合起来能产生怎样的火花。

如果你仔细观察刚刚在地平线上升起的月亮，你就会发现月亮特别大，就好像在你触手可及的地方。但换一种方式看，就不一样了。只要把一张纸卷成一根水管的形状，来一次“管中窥月”，你就会发现，地平线上的月亮并不如原来那么大了。

这种现象就是著名的庞佐错觉。地平线附近总会有许多我们熟悉的事物，例如山脉、房屋、大树等。对比之下，月亮就会显得大很多。“管中窥月”这样的方式，可以消除地平线周围事物带来的影响。

对于初升的月亮来说，从眼前延伸至地平线，地面景物与地形逐渐缩小，在我们的视野中起到了汇聚线的作用，而扁平的天空也让我们觉得地平线上的月亮要比头顶上的月亮更远。但月亮的视角是恒定的，地平线上的月亮和头顶上的月亮在视网膜上的投影面积是相等的，庞佐错觉效应使得大脑做出了“ 地平线上月亮更大”的判断。