基于自适应精确罚函数的分布式资源分配算法

时侠圣,徐 磊,杨 涛

(1.中国矿业大学地下空间智能控制教育部工程研究中心,江苏徐州 221116;2.东北大学流程工业综合自动化国家重点实验室,辽宁沈阳 110819)

1 引言

由于网络系统在许多应用场景中都具有重要应用前景,比如传感器网络、智能电网、机器人编队等,多智能体系统控制和优化在近年来受到越来越多的关注[1-2].而关于多智能体系统的分布式优化问题更是热点之一.分布式优化旨在通过智能体间的信息交互实现某些决策量或者行为量的最优一致性.到目前为止,许多学者已对分布式优化问题进行深入研究[3-6].事实上,上述大部分成果都与设计分布式优化算法相关,而智能体动力学特性并没有受到太多关注.随着信息物理系统技术和控制理论技术发展,近年来越来越多基于智能体动力学特性的连续时间分布式优化算法得到广泛研究.例如,文献[7]基于增广拉格朗日乘子法和事件触发通信机制设计一类无约束分布式优化算法,确保算法收敛的同时减少不必要的通信资源浪费.此外其他类型的智能体动力学特性也得到广泛研究,包括单积分系统[8-9]、双积分系统[10]、欧拉-拉格朗日系统[11]、线性多智能体系统[12]和非线性多智能体系统[13]等.

作为分布式优化领域最重要的分支之一,分布式资源分配问题因其广泛的应用前景而受到极大关注.例如通信网络[14]和能源系统[15]等.在资源分配问题中,智能体不但要最小化成本函数,此外也受到一些局部约束和全局等式约束.首先针对不含局部不等式约束的资源分配问题,很多优秀的连续时间分布式优化算法被设计出来,包括固定时间收敛算法[16]、预定义时间收敛算法[17],以及基于一阶多智能体系统[18]、二阶多智能体系统[19]、高阶多智能体系统[20]、线性多智能体系统[21]和非线性多智能体系统[22]等的分布式优化算法.然而智能体局部约束广泛存在于实际系统中,比如经济调度中发电机组输出功率存在上下限等.因此在算法设计时势必要将智能体局部约束考虑进来.

为求解资源分配问题中的局部约束,文献[23]首先将微分映射算子引入进来,在算法执行时,每个智能体都需要计算梯度在约束集上的切锥,因而增加一部分计算负担.同时,直接计算梯度到约束集的投影,该文献也设计一类基于映射算子的分布式资源分配算法.该类方法受到学者广泛关注和再创新,目前已构建很多不同特色的分布式优化算法,包括微分映射算子法[24-26]和映射算子法[27-34].映射算子虽然可以很好地解决资源分配问题中局部不等式约束,然而映射算子法的微分包含解有可能不存在.为避免映射算子的引入,若智能体局部约束为凸不等式约束时,基于KKT 最优性约束条件,文献[35]对局部不等式约束建立等价的等式约束方程,设计自适应控制算法,实现不等式约束条件求解.该类方法也被称为鞍点法[36-38].近年来,由于罚函数法可以将智能体局部约束转移至成本函数中,因此罚函数法受到学者广泛关注.文献[39-42]等和文献[43]分别利用∊-精确惩罚函数法和θ-罚函数法,将局部不等式约束转移至成本函数中,实现局部不等式约束求解.该方法也被称为内点法或者障碍函数法.对于该类精确罚函数法,必须对罚函数设计合理的惩罚因子,否则算法可能无法收敛至最优解.此外上述惩罚因子需提前获知,且无法实现自适应获取.

为此,受文献[44]启发,本文拟利用距离函数设计一类基于精确罚函数法的分布式资源分配算法.本文贡献点可总结如下: 1)将基于距离函数的精确罚函数法引入分布式资源分配问题中,设计一类新型分布式优化算法.与文献[45]不同,本文所设计算法无需智能体间交互局部成本函数梯度信息,实现智能体隐私保护;2)不同于内点法设计思想[39-43],本文所设计算法利用自适应控制思想避免对全局成本函数先验知识的获取,无需手动调整惩罚因子大小;3)基于跟踪控制技术,本文将所设计算法推广至二阶多智能体系统,实现二阶多智能体系统分布式资源问题的最优分配.

本文的结构安排如下: 第2节主要介绍网络拓扑、问题描述和非光滑分析等;第3节中给出全文主要内容,即算法设计和对应的收敛性分析;第4节提供两个案例仿真;总结部分在第5节给出.

符号说明:现将后续所需符号及定义说明列于下表1.

表1 符号说明Table 1 Symbol description

2 基础知识

2.1 图论基础知识

假设1在本文所研究资源分配问题中,系统通信网络G为连通图.

假设1是无领导者多智能体系统分布式优化问题的必要条件,以保证多智能体各局部信息的全局性流通,确保全局最优解的获取.

2.2 问题描述

在本文所研究资源分配问题中,假设系统存在n个智能体.每个智能体都拥有一个仅自身知晓的局部成本函数fi(xi):Rm →R,以及局部资源需求量piRm.此外,在实际系统中,智能体实际分配资源量都存在约束范围Ωi.以智能电网经济调度问题为例,各发电机组都有自己的发电能力范围.而资源分配问题就是如何在各智能体约束范围内以最低成本实现全局资源量最优分配.典型地,资源分配问题数学模型归纳如下:

不同于文献[46]的二次成本函数,本文成本函数fi(xi)为更一般凸函数.此外,本文考虑的局部有界约束集Ωi包括文献[39-41]中箱式约束和文献[35]等一般不等式约束.在智能电网中,pi为各发电厂所负责区域用电量的短期预测值,该值可利用以神经网络算法为主的智能优化算法结合用户侧历史用电数据预测得到[38].而智能电网经济调度问题旨在满足各发电机组自身约束范围时完成一定发电量部署以实现总发电成本最低.

为解决上述问题,以下假设和引理被广泛应用于已有资源分配算法设计中[32,35].

注1引理2中最优解的充要条件表达形式与已有文献一致[24,26,29,32].为避免歧义,其等价形式如下:

引理3[44]对于局部约束集Ωi,距离函数d(xi,Ωi)inf{‖xi-y‖,∀y Ωi}为凸函数且其梯度定义为

很显然,若xi Ωi,则有∂d(xi,Ωi)⊂NΩi(xi).

借助距离函数d(xi,Ωi),将资源分配问题修改如下:

2.3 微分包含

一微分包含系统给定如下:

其中F是定义为从Rq到其子集的集值映射关系.对于几乎任意[0,t1],若存在一绝对连续映射x:[0,t1]→Rq满足系统(5),则称x是其Caratheodory解.系统(5)的平衡点记为Rq|0q F(x)}.假定V:Rq →R是局部李普希茨连续,且V(x)在系统(5)的集值Lie微分定义为

对于系统(5),若F是局部有界、上半连续,且取值为非空、紧致和凸值,则对于任意初始状态,系统(5)都存在Caratheodory解[44].

引理4[44]令V:Rq →R是局部李普希茨正则函数,且W ⊂Rq是系统(5)的紧和强不变子空间.假定系统(5)的所有Caratheodory解都有界,SVRq|0(x)},M是∩W的最大弱不变子空间,其中¯SV是SV的闭包.若存在TT(φ(0))≥0对任意t≥T使得maxLF(V(φ(t)))≤0,那么φ(t),t≥T收敛至M的最大弱不变子空间.

3 算法设计及收敛性分析

3.1 一阶多智能体系统

基于增广拉格朗日乘子法,为求解带等式约束分布式资源分配问题,通过给每个智能体分配局部拉格朗日乘子λi,并利用比例积分控制思想对局部拉格朗日乘子建立迭代规则,最终促使所有局部拉格朗日乘子收敛至引理2中最优拉格朗日乘子进而利用梯度下降法实现资源最优分配.基于此,算法设计如下:

注2由于问题(4)中存在全局等式约束,而拉格朗日乘子法恰是解决等式约束优化问题的有效途径.且引理2中是全局性拉格朗日乘子,所以需要给每个智能体设置一局部拉格朗日乘子λi(亦称之为对偶变量),其次结合多智能体系统一致性实现局部拉格朗日乘子趋同.更具体地,在式(7b)中,项-β(L ⊗Im)λ确保局部拉格朗日乘子一致性.由于最优资源量与局部资源需求量pi一般情况下是不同的,此时利用对偶变量的历史信息zi来平衡两者之间差值.此外,xi-pi也被证明是对偶变量λi的梯度信息[47].因此式(7b)是结合梯度下降法与比例积分控制思想.在(7a)中,智能体由各局部梯度项-∇fi(xi)驱动,而对偶变量λi则是将智能体由局部最优解牵引至全局最优解.此外,结合式(7d),ci∂d(xi,Ωi)则保证智能体局部约束成立.以智能体xi处在约束集Ωi左侧为例.由式(7d)可知此时ci继续增大,项ci∂d(xi,Ωi)＜0 且继续减小.所以式(7a)右侧大于零,迫使xi增大向约束集靠近.

其次,分析算法(7)平衡点与问题(4)最优解的关系.

引理5若(x*,λ*,z*,c*)是算法(7)的平衡点,则x*是问题(2)的最优解.反之亦成立.

现在给出算法(7)收敛性分析.

证毕.

定理1若假设1和2成立,则算法(7)收敛至问题(2)的最优解,且控制参数收敛范围为α ＞0＜β ＜

证将算法(7)右侧记为Ψ.令李雅普诺夫函数为V(t,x,λ,z,c)V1(t,x,c)+V2(t,λ,z)+V3(t,x,λ,c),其中:

其中t≥T(x0,λ0,z0,c0).在上式分析中利用了以下不等式:

结合ζ1,ζ2,ζ3的任意性可知,对任意t≥T(x0,λ0,z0,c0)有

由式(15)可知对于t≥T(x0,λ0,z0,c0)＞0,x(t),λ(t),z(t),c(t)有 界.令K{(x,λ,z,c)|V(x,λ,z,c)≤V(x0,λ0,z0,c0)},且M ⊂K ∩{(x,λ,z,c)|0(x,λ,z,c)}是最大弱不变集.

最后,证明系统(7)生成的轨迹x(t)收敛至问题(2)最优解.给定任意初始值,存在有界轨迹(x(t),λ(t),z(t),c(t)).所以存在一个升序时间序列{tr}使得

由式(19)可知,对任意ε＞0,∃tr ＞0使得

进而有

因此,有

即x(t)收敛至问题(2)的最优解.证毕.

注3基于映射算子PΩi(.),已有很多文献对问题(2)进行深入探讨.然而如文献[44]所述,基于映射算子的分布式优化算法很难检查其Catheodory解是否存在,因为映射操作也许是非凸的.而与已有的内点法算法相比,本文所设计算法不需要提前获知惩罚因子大小,避免对先验知识获取[39-43].同样基于距离函数,文献[45]所设计的分布式资源分配算法需要智能体间交互局部成本函数梯度信息,降低算法隐私性.此外,该文献亦要求算法在初始状态时就必须满足等式约束.而本文所设计算法可实现初始状态自由,且智能体之间仅交互拉格朗日乘子信息.

3.2 二阶多智能体系统

当所考虑系统为二阶多智能体系统时,利用跟踪控制技术,算法设计如下:

其中控制参数α,β,k为正数.在上式中,辅助变量y收敛至问题(2)最优解.然后利用跟踪技术令智能体资源量x趋向于y,最终实现问题最优解获取.此外,变量xi,λi初始值可自由设定,变量zi,ci设定为零初始.

定理2若假设1和2成立,则算法(24)收敛至问题(2)最优解,且控制参数收敛范围为α＞,0＜β ＜,k ＞3.

证令李雅普诺夫函数为

其中V1,V2,V3与定理1类似,而V4定义如下:

显然V关于变量(x,v,y,λ,z,c)是半正定的.任取ζ44,则有

在上式中利用了如下不等式:

类似于定理1,有结论

其中t≥T(x0,λ0,z0,c0).余下分析与定理1一致,在此予以省略.证毕.

注4在已有分布式资源分配算法,文献[26,38,40]针对二阶多智能体系统设计相应的微分映射算子算法、映射算子算法和∊-精确罚函数法.其中文献[40]中惩罚因子过小会导致算法在稳定点时产生波动,且该方法只能解决一维资源分配问题;文献[26]通过奇异摄动法和微分映射算子解决局部不等式约束,增加计算量的同时并没有给出摄动参数收敛范围.另外该算法要求智能体初始状态也必须在局部约束范围内;文献[38]通过使用映射算子避免局部约束切向锥的求解,但基于符号函数的固定时间收敛理论的引入增加算法分析难度,且该方法无法定量分析算法稳定点的最优性.此外,与文献[26,38]的跟踪算法不同,本文所设计算法(24)没有利用到虚拟变量yi的二阶导信息,降低算法复杂度.

注5文献[19]针对二阶智能体设计一种无局部约束分布式资源分配算法,并在智能电网经济调度问题上做了仿真验证,其中发电机组可视为如下二阶系统:

其中:Tmi,Tei,Kmi是与涡轮发电机系统相关的参数,Pi,为输出发电量和涡轮发电机控制输入,Xei为系统开环值.通过反馈线性化理论,上述发电机控制输入可设计为

其中ui为本文所设计控制策略.从算法(24)可得到ui-kvi-(Pi-yi),进而实现基于涡轮发电机系统的经济调度问题.

4 案例分析

本小节通过一组案例仿真来验证所设计算法的有效性.案例数据来自文献[45],其中第1个案例为一维经济调度问题,包含6个智能体节点,且通信网络为无向环图.智能体局部成本函数定义为fi(xi)+bi|xi-γi|+ci,其中xi表示发表机组输出功率,单位为MW.ai,bi,ci,γi为发电机组成本参数,总结在表2中.

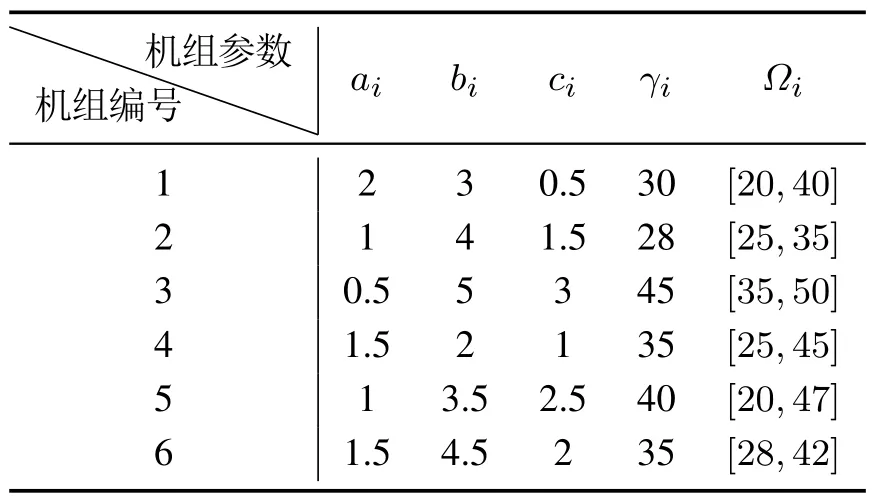
表2 发电机组参数Table 2 The parameters of each agent

图1 案例1中算法(7)发电机功率轨迹图Fig.1 The power trajectories xi(t)in case 1 with algorithm(7)

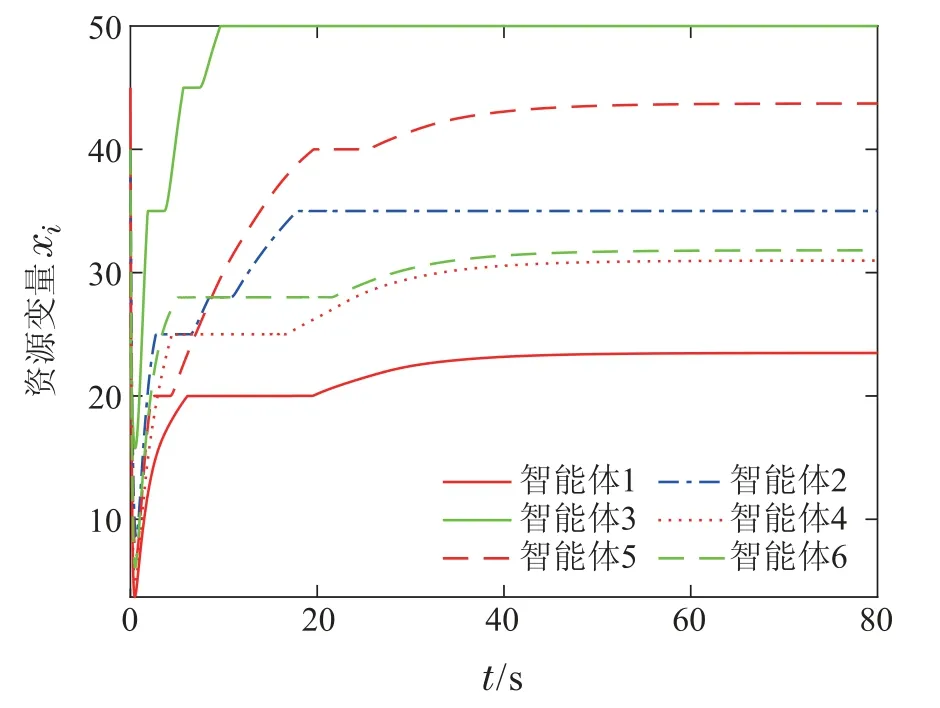
图2 案例1中算法(24)发电机功率轨迹图Fig.2 The power trajectories xi(t)in case 1 with algorithm(24)

为分析本文所设计算法优越性,针对一阶多智能体系统,本文算法(7)与文献[31]映射算子法、文献[24]微分映射算子法、文献[23]映射算子法、文献[39]精确罚函数法和文献[35]鞍点法等的收敛轨迹对比如图3所示,其中误差e定义为e(t)并且各算法控制参数采用原文章中案例设置值.

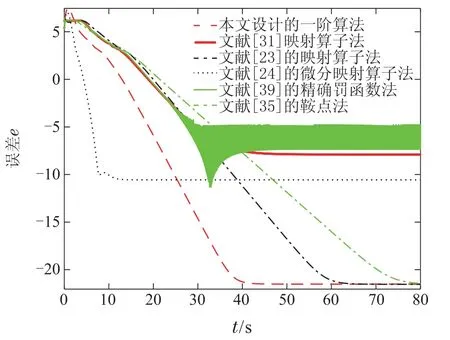
图3 已有一阶多智能体系统分布式资源分配算法收敛轨迹图Fig.3 The convergence trajectories ei(t)for the existing distributed resource allocation algorithm over first-order multi-agent systems

从图3可以看出,文献[39]的精确罚函数法容易导致算法在稳定点处发生轻微波动,且收敛速度较慢.而文献[35]和文献[23]可以实现较高收敛精度.由于已有文献采用类似设计框架,当设置同样控制参数时算法收敛速度大致相当.此外,本文算法(7)中参数α能够调节λ*,所以可以通过降低α值进而降低λ*值,从而提高算法收敛速度.定理1分析过程中可以给出更宽收敛范围,即α ＞.所以本文所设计算法在面对较大强凸系数的资源分配问题具有较快收敛速度.而针对二阶多智能体系统,本文算法(24)与文献[26]微分映射法和文献[38]映射算子法的收敛速度轨迹图展示如图4所示.

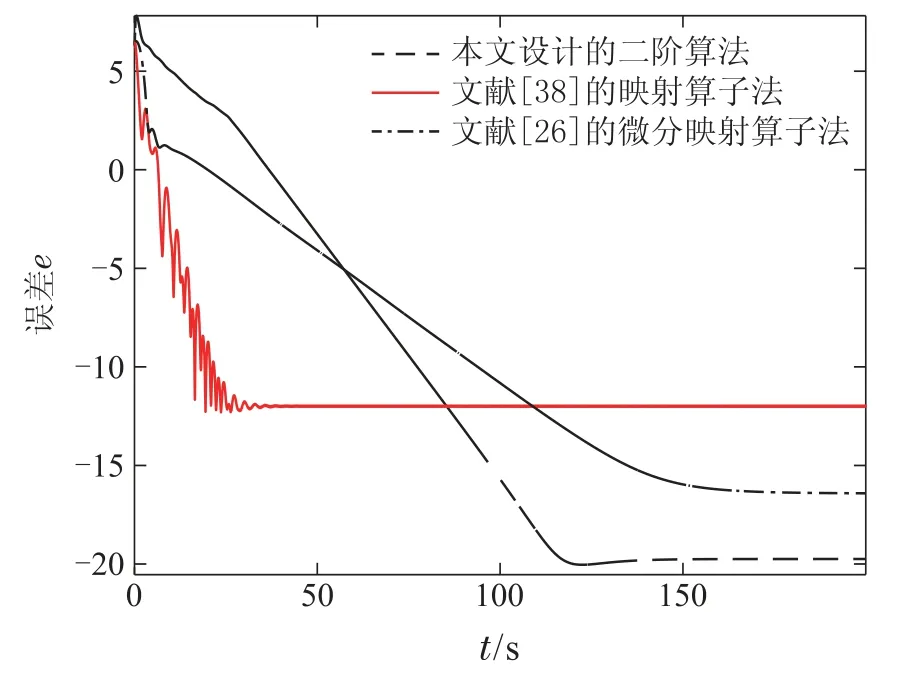
图4 已有二阶多智能体系统分布式资源分配算法收敛轨迹图Fig.4 The convergence trajectories ei(t)for the existing distributed resource allocation algorithm over secondorder multi-agent systems

从图4可以看出,由于文献[38]利用固定时间收敛理论加速算法的收敛速度,所以其收敛速度最快,但符号函数和幂函数的引入也致使其稳定点精度有限.由于文献[26]利用摄动法分析算法的收敛性.为确保算法收敛,摄动参数理论上无限小.但是较小摄动参数导致算法收敛速度较低.与之相比,本文所设计算法在保证稳定点具有较高精度的同时算法也具有较快的收敛速度.

其次,对一个二阶多智能体系统进行案例仿真[38],其中4个智能体的局部成本函数和约束定义如下:

此外该系统的网络连接拓扑也假定为环图.等式约束为p[7 13]T,令控制参数α1,β0.5,则算法(7)的轨迹如图5所示.其中星号∗表示上述二维分布式资源分配问题的理论最优解,(1.8884,3.4729),x2(1.8237,1),(1.4396,4.5604),(1.8483,3,9666).

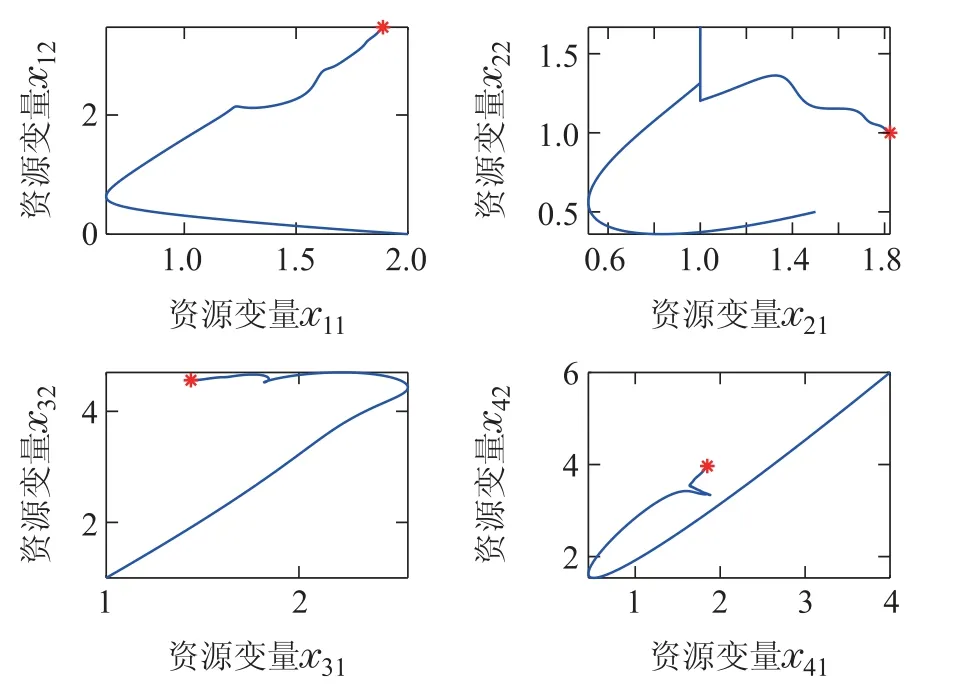
图5 案例2中算法(24)各智能体轨迹图Fig.5 The trajectories xi(t)for each agent of algorithm(24)in case 2

与案例1类似,定义算法轨迹x(t)与理论最优解x*误差e(t),并将其展示在图6中.从图5和图6可以看出,本文所提算法对二维及以上资源分配有效.

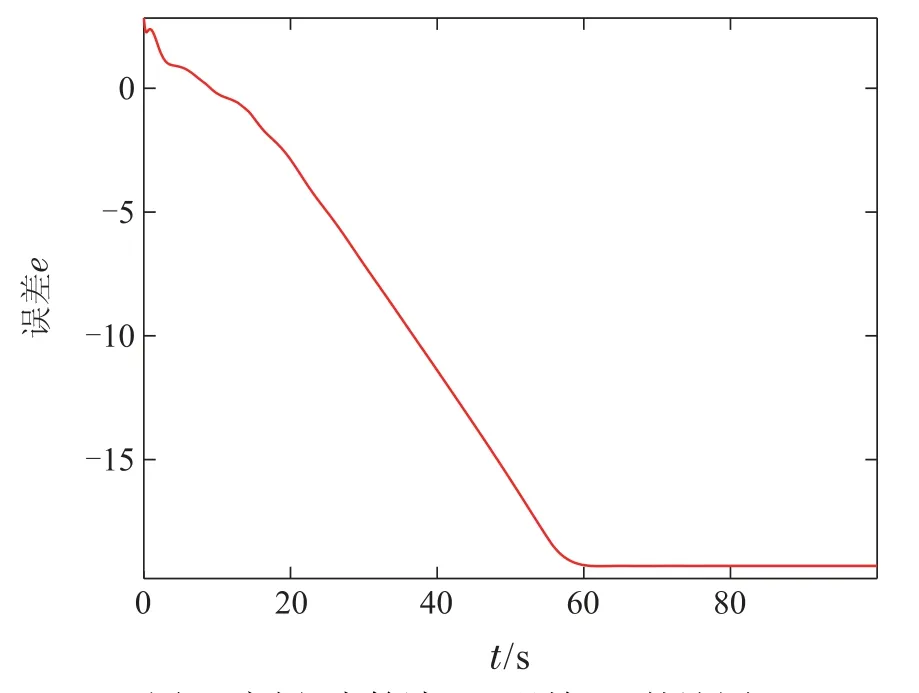
图6 案例2中算法(24)误差e(t)轨迹图Fig.6 The trajectories e(t)of algorithm(24)in case 2

5 结论

在资源分配问题中,智能体局部约束增加了算法分析的难度.为确保算法Catheodory解一定存在,结合智能体动力学特性,本文设计一种新型一阶分布式资源分配算法,其中算法利用距离函数表征各智能体的局部约束,并利用距离函数设计自适应控制策略,避免算法使用到全局成本函数的先验知识.此外,利用跟踪控制技术将算法推广至二阶多智能体系统.未来会进一步考虑通信延迟或者事件触发通信对算法设计的影响,并研究自适应控制参数设计.