轮询通信协议下信息物理系统分布式状态估计

朱凤增彭 力

(1.江南大学物联网应用技术教育部工程中心,江苏无锡 214122;2.临沂大学自动化与电气工程学院,山东临沂 276005;3.无锡太湖学院物联网应用技术重点建设实验室,江苏无锡 214063)

1 引言

近年来,在航空航天、医疗保健、交通、民用基础设施和智能电网等行业,广泛采用了信息物理系统(cyber-physical systems,CPSs)[1-7].通过整合计算、通信和控制,这样的CPS将网络世界(如信息、通信)与物理世界联系起来,具有丰富物理/虚拟世界的人机交互.工业CPS是一类大规模、地理上分散、联合协作的系统,其中大量的传感器和执行器被嵌入并联网以实现动态监测和闭环控制.作为不可或缺的组成部分,传感器网络通常无缝集成到工业CPS中,以方便实时感知、监测和控制.实际工程中,传感器节点与子系统或分布式执行器一起分散地部署在预定的区域中[8].基于无线传感器网络的分布式滤波算法,实现了CPS的一致性状态估计和感知.在这些信息的帮助下,执行器网络可以实现对物理系统精确地实时控制.

目前,基于无线传感器网络的分布式滤波算法主要包括:分布式Kalman滤波[9-10]和分布式H∞滤波.由于分布式H∞滤波方法不要求精确的系统模型和外部噪声的统计特性,因此在CPS分布式状态估计问题上发挥着重要作用.近年来,有关分布式H∞滤波取得了众多研究成果[11-14].例如,文献[11]解决了受测量饱和网络攻击影响的传感器网络分布式事件触发H∞滤波问题.文献[12-13]针对传感器网络信道衰退和量化测量,分别设计了分布式鲁棒H∞一致性状态估计器.

需要指出的是,在复杂的网络环境中,节点随机故障、通信链路的不稳定、障碍物阻塞、不确定的网络诱导现象等,往往会导致滤波器网络通信拓扑的变化[15-18].基于固定网络通信拓扑设计分布式滤波算法,在实际应用中也将受到限制.为了解决这一问题,文献[15]解决了拓扑切换下线性异构多智能体输出调节问题.文献[16]基于自适应事件触发机制设计了分布式鲁棒滤波器.文献[18]研究了动态事件触发机制下一类离散非线性时变系统的递归分布式滤波问题.系统输出通过受时变拓扑约束的传感器网络感知,其拓扑通过Gilbert-Elliott通道连接并遵循Markov随机变化过程.然而,这些研究成果均是基于齐次Markov理论实现通信拓扑随机变化的建模.采用齐次Markov链建立的拓扑切换的数学模型,往往可以简化系统分析和设计.但是,为一个复杂的无线滤波器网络获取一个完整且精确地拓扑变化的转移概率数据,往往需要耗费大量的时间和精力,同时网络拓扑变化规律可能呈现非线性.例如,在一个海洋石油渗透监测系统,数百个节点组成的传感器网络被部署在海洋中执行实时监测任务.然而,在海浪、洋流、潮汐、台风和船只等影响下,这不可避免地造成节点的随机移动和时变的通信网络[19].这种时变通信拓扑在网络的不同运行周期往往表现出随机性、模糊性和复杂性,即无法通过单一的拓扑切换概率矩阵描述其切换规律.因此,与其执着于获取系统整个运行周期单一的拓扑切换概率模型,不如研究具有多个拓扑切换概率矩阵、更具一般性的拓扑切换概率模型,这对实际工程应用具有重要意义,这是本文研究的第1个动机.

另一方面,随着网络技术的快速发展,许多通信协议被应用于实际工程中,有效地利用有限的网络带宽.一些被广泛应用的通信协议主要包括:尝试一次丢弃协议、轮询协议(Round-Robin)和随机通信协议[20-23].需要指出的是,轮询协议是一类周期性调度方案,已经在许多通信系统中广泛实施,能够缓解大量通信数据拥堵,节省通信成本.在过去的几年里,轮询协议的滤波/控制问题逐渐成为一个有吸引力的研究课题.例如,文献[21]研究了一类轮询通信协议下具有时变延迟的复杂网络系统状态估计问题.通过使用一组矩阵不等式,得出了一个约束估计误差的充分条件,以保证滤波误差系统最终均方指数有界.然而,在分布式滤波网络拓扑随机切换背景下,基于轮询协议的传感器网络CPS状态估计问题还没有得到充分的研究,这是本文研究的另一个动机.

总结上述讨论,本文旨在解决具有时变拓扑的CPS状态估计问题.本文的主要贡献如下:1)所考虑的分布式滤波网络拓扑遵循非齐次Markov随机变化规律,因此文献[12,14]所采用的固定拓扑模型,以及文献[17-18]所采用的齐次Markov型切换拓扑模型,均可以认为是本文的一种特殊情况;2)为了避免数据冲突和充分利用传感器网络有限带宽,为传感器网络引入了轮询通信协议,每个传感器节点将测量信号分量周期性传输给相应的滤波器,不同于文献[11],文献[13,16]采用的事件触发机制,本文采用的轮询通信协议不仅可以避免大量节点同时通信可能造成的数据冲突,也不占据任何计算资源;3) 基于随机分析方法,建立了分布式滤波器存在的充分条件,滤波误差系统满足均方指数最终有界;4)在最小化输出估计误差渐近上界的基础上,获得期望的分布式滤波器参数.

2 问题描述

Markov随机变量r(k)代表k时刻的拓扑结构,r(k)在一个有限集合S{1,2,...,n0}中取值,其时变的状态转移概率矩阵为Π(k)πst(k)代表k时刻子拓扑s切换到子拓扑t的概率,并满足

注1每个子拓扑可视为一个“模态”,子拓扑之间的跳跃也就是“模态”之间的切换,切换规则由Markov过程(连续时间域)或Markov链(离散时间域)描述.模态之间的切换概率是由模态转移概率矩阵或转移速率矩阵决定的.若转移概率元素πst(k)不随时间变化而变化,则称r(k)为齐次Markov链,否则称为非齐次Markov链.

考虑一类CPS的物理层具有如下离散形式:

假设系统(3)的状态是由N个估计节点组成的滤波网络观测,而滤波器节点i通过相应的传感器节点实现对系统的感知测量,具体地描述为

其中yi(k)[yi1(k)(k)]是节点i测量向量.此外,系数矩阵A,B,E,M,Ci,Di均具有适当的维数.

假设1在无线传感器(滤波器)网络中,节点之间通过交换包含时间戳的信息包可以实现时钟同步状态.

假设2假设外部干扰v(k)满足以下的范数有界约束:

如图1所示,在一个具有随机切换拓扑的传感器网络中,每个传感器节点对应一个远程分布式状态估计器.由于每个测量节点上都配备了多个传感器实现系统感知测量,这不可避免地导致了高阶测量(即,yi(k)).然而,对于无线信道来说,信息是以数据包为单位形式进行传输的,其中数据包的大小是有限的[24-25].因此,大量的传感器节点同时上传所有采样数据是不切实际的.在这种情况下,轮询通信协议是一种处理数据包大小限制约束的有效方式.

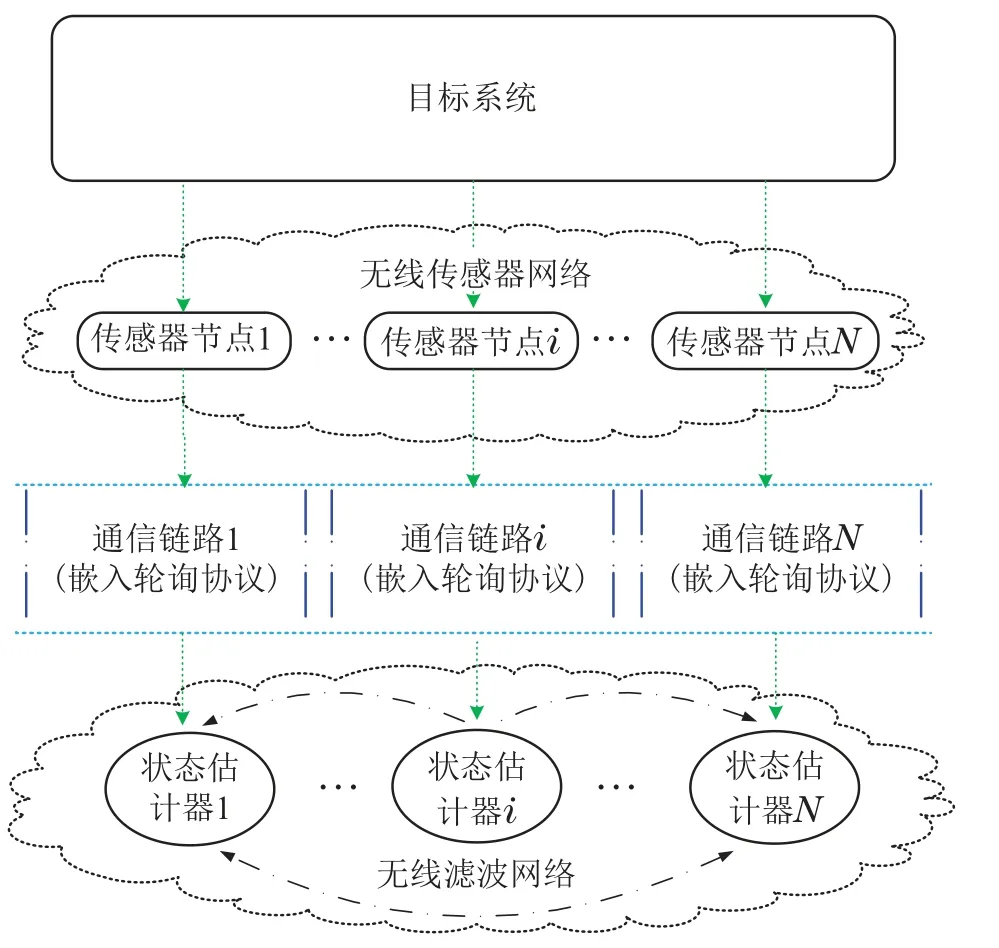
图1 带有轮询通信协议的分布式滤波系统Fig.1 Distributed filtering system with Round-Robin communication protocol

依据文献[20],在轮询协议下,每个传输时刻只允许一个节点分量传输测量数据,每个节点分量的传输机会是按循环顺序平等分配的.因此,实际被传输的测量可以描述为

其中

定义函数δ(.):当l0时,δ(l)1;当l/0时,δ(l)0.因此,如果k-m ＜0,则ħ(k-m)m;如果k0,则ψ0ny.此外,假设∀k≤0,有yi(k)yi(0).

根据式(6)可以得到以下更新规律,该规律用于描述传感器网络与滤波器网络之间的信息传输

假设滤波网络具有时变和切换的拓扑结构,其变化过程遵循Markov随机过程.构造如下拓扑依赖的分布式滤波器:

注2采用时间触发协议或事件触发协议下的传感器网络,每个传感器节点都根据自己的传输标准发送数据,而这些传感器之间没有协调.一旦传感器网络的某个采样瞬间只有一条信道可用,则可能导致节点间通信数据冲突、信道拥堵等问题.为了解决该问题,轮询通信协议被广泛用于协调传感器之间的数据传输.在该协议的调度下,网络节点依据预先设定的规则,依次获得访问通信网络的权限.接收端通常采用零阶保持器(zero-order holder,ZOH)保存传输数据,以便在接收端保留最新的传输信息.此外,需要指出的是,由于轮询通信协议是一种静态的周期性调度方案,因此在数据传输过程中不消耗任何计算资源.

注3本文提出的分布式滤波方法适用于一类通信受限、低成本和高鲁棒性状态估计应用领域.随着通信技术的发展,特别是近几年发展起的5G通信技术,虽然网络通信的性能得到大幅度地提高,但是传感器网络大多采用成本低廉的无线传感器模块组成,广泛采用蓝牙、LoRa和NB-IoT等通信技术,因此在实际的工程应用中需要考虑网络通信能力的约束.如文献[26]开发的校园班车运行实时监控系统,采用了LoRa通信作为一种低成本的替代方案,并且为了避免信道拥塞和数据冲突,每个LoRa 终端收集器以轮询通信方式与所有的采集装置节点通信.

为方便分析,考虑N个节点,定义k时刻系统状态向量

参数向量

以及滤波器增益矩阵

其中

定义

以及

则可以得到带有轮询通信协议的系统动态方程

其中:

以及带有轮询通信协议的滤波网络动态方程

其中:

定义1如果存在常数0 ≤α ＜1,β ＞0和δ ＞0,使得

那么估计误差动态系统方程(19)是均方意义下指数最终有界的.此外,α和δ分别表示e(k)的衰减率和渐近上界.

本文主要研究目标是为基于无线传感网络的信息物理系统(3),设计分布式状态估计器(9),使得增广滤波误差系统(19),同时满足以下两个性能要求:

a) 当存在噪声w(k)和外部干扰v(k)时,估计误差系统(19)是均方意义下指数最终有界的;

引理1令Qdiag{Q1,Q2,...,Qn},其中QiRp×p,1 ≤i≤N是可逆矩阵,若Rnp×nq,XQW,则有.

3 滤波误差系统稳定性分析

在这一节中,给出了保证增广滤波误差动态系统(19)满足均方意义下指数最终有界的充分条件.此外,通过解决一组线性矩阵不等式约束下的优化问题,可以获得期望的分布式滤波器参数.

定理1给定分布式状态估计器参数和,.假设存在正定矩阵P(m,s)＞0,Q(m)＞0,正实数ρ,使得以下矩阵不等式成立:

其中:

则增广滤波误差系统(19)的解是均方意义下指数最终有界的.

证为了分析滤波误差系统(19)满足均方意义下的有界,选取以下Lyapunov函数:

其中:

首先,计算V1(k)的前向差分

其中

因此,可以得到

其中:

然后,计算V2(k)的前向差分,

同样的,可以得到

其中:

结合式(26)和式(29),存在一个正实数ρ,使得

其中

由不等式(21)可知Λ ＜0.因此,式(31)可以转化为

其中

根据不等式(33),可知对任意正实数σ ＞0,可以推导出

进一步地,式(36)等价于

因此,根据定义1可知,增广滤波误差系统(19)的解是均方意义下指数最终有界的.并且,滤波网络的估计误差渐近上界为

证毕.

4 分布式滤波器设计

定理1给出了滤波误差系统均方意义下最终有界的充分条件,并且得到滤波误差系统衰减速率的下界为1-1/ρ.实际工程应用中,衰减速率是评估系统性能的一个重要指标.本节将给出在给定一个期望的衰减速率条件下获得分布式滤波器参数的方法,并满足输出估计误差的渐近上界最小.

其中:

那么,滤波误差系统(19)是均方意义下是指数有界的,且期望的分布式滤波增益可以经过两次计算得到:

步骤1首先,计算并得到滤波增益复合矩阵,

证针对滤波误差系统(19),重新构造以下Lyapunov函数:

与定理1证明过程类似,经推导可以得到

其中:

以及

定义

式(38)(43)-(44)和式(49)经过Schur补引理可以转化为

因此,可以得到

由不等式(39)-(40),很容易得到

根据不等式(52)-(53),可以得到

因此可以证明,滤波误差系统(19)是均方意义下指数最终有界的.

此外,为了解决输出估计误差渐近上界的最小化问题,考虑不等式约束(41),则有

满足约束条件(38)-(41).

算法1给出了在最小化误差渐近上界的同时,获取相应分布式滤波器增益的计算流程.

算法1求解最优的误差渐近上界和相应的分布式滤波器参数.

步骤1给定系统(3)初始参数,期望的衰减速率下界¯α;

步骤2定义决策变量P(m,s),Q(m),V1,V2,

步骤3描述不等式约束条件(38)-(41);

步骤4利用MATLAB YALMIP工具箱,MOSEK求解器,迭代计算优化目标F*;

步骤5当目标优化函数F*最小时,停止迭代寻优过程,输出此时决策变量;

步骤6通过式(43)-(44)计算得到分布式滤波器参数,以及计算得到最小的输出估计误差上界.

5 仿真例子

在这一节中,通过两个数值仿真例子证明所设计的分布式状态估计器有效性.

例1选取目标系统(3)的参数如下:

考虑一个由4个节点组成的传感器网络实现系统的感知与测量,每个节点的参数如下:

假设噪声w(k)N(0,1),该噪声w(k)是一个满足均值为0,方差为R1的一维高斯白噪声;外部干扰输入为v(k)sinke-0.1k;选取增广滤波误差衰减速率0.88.此外,系统的初始状态和滤波器的初始状态均为零;初始的通信拓扑r(0)1.

如图2所示,假设滤波器网络具有两种时变的通信拓扑,拓扑切换概率矩阵Π(k)由以下两个概率矩阵组成:

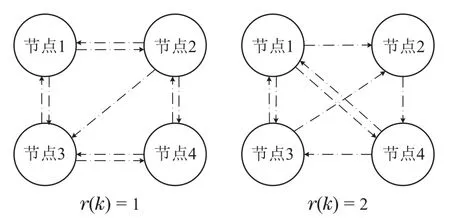
图2 滤波器网络通信拓扑Fig.2 Filtering network communication topologies

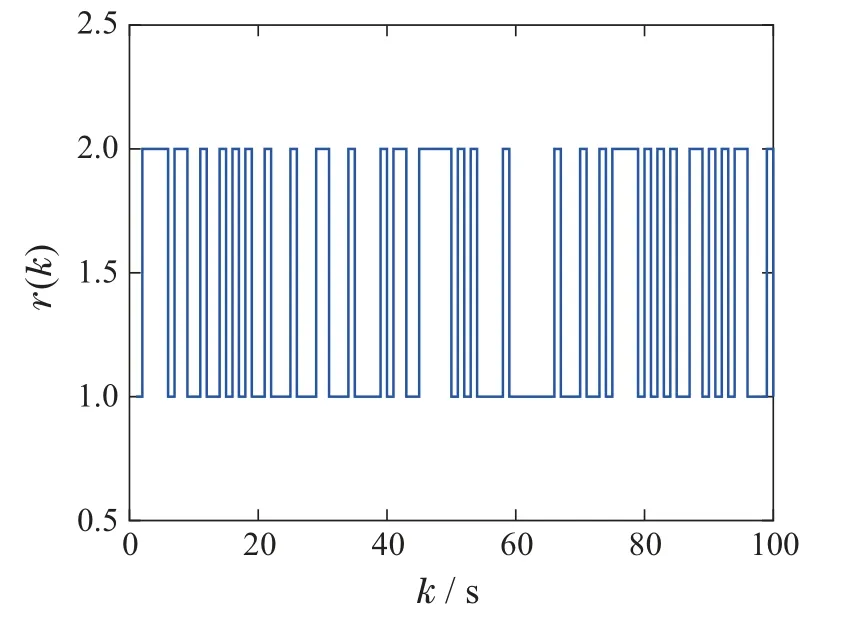
图3 非齐次Markov链Fig.3 A non-homogeneous Markov chain

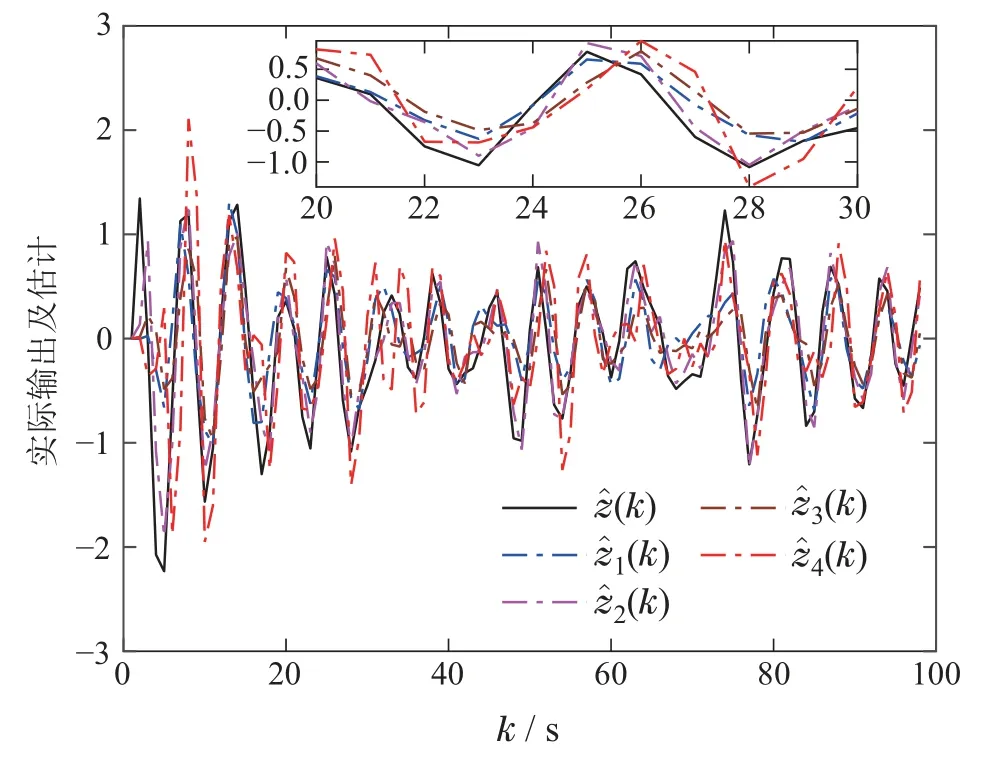
图4 系统实际输出z(k)与滤波节点的估计(k),i1,2,3,4Fig.4 Actual system output z(k) and estimated output(k),i1,2,3,4

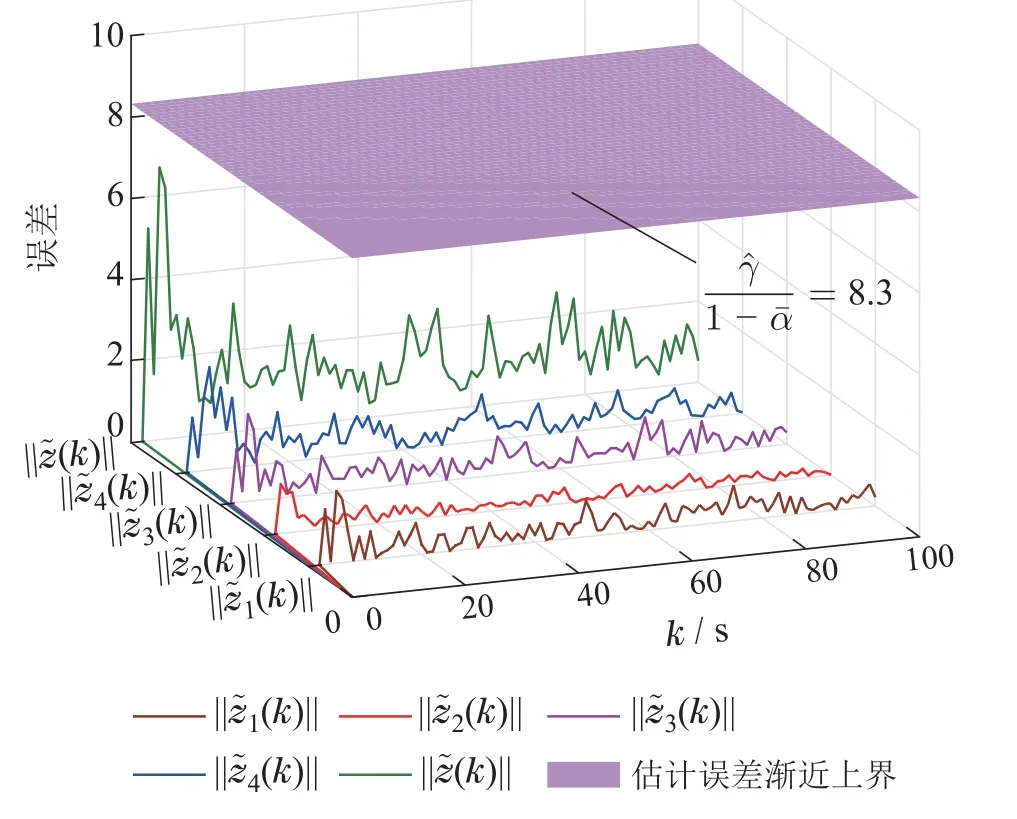
图5 滤波网络估计误差Fig.5 Estimation error of the filtering network

为了进步研究轮询协议与滤波性能之间的关系,针对测量节点1和3,定义以下6种情形:

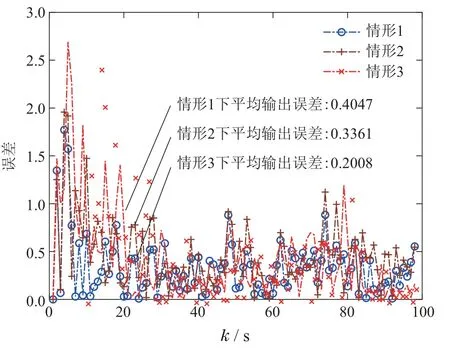
图6 节点1在不同情形下估计误差对比Fig.6 Comparison of estimation errors at node 1 under different cases

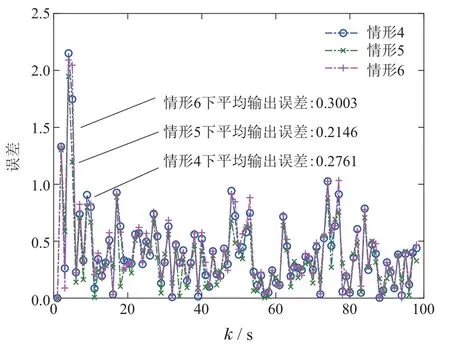
图7 节点3在不同情形下估计误差对比Fig.7 Comparison of estimation errors at node 3 under different cases

在轮询协议下,采用情形1实现目标系统的感知与测量,则滤波节点1可以周期性获得系统状态x1(k)和x2(k)的测量数据,最终实现的平均输出误差为0.2008;采用情形2实现目标系统的感知与测量,则滤波节点1仅可获得系统状态x1(k)的测量数据,最终实现的平均输出误差为0.3361;采用情形3实现目标系统的感知与测量,则滤波节点1仅可获得系统状态x2(k)的测量数据,最终实现的平均输出误差为0.4047;采用情形4-6实现目标系统的感知与测量,则滤波节点3均可获得系统状态x1(k)和x2(k)的测量数据,最终实现的平均输出误差分别为0.2761,0.2146和0.3003.

仿真结果表明,若高维测量中每个测量分量仅能感知与测量目标系统的部分状态时,采用轮询协议可以实现估计节点获得更为全面的系统状态信息,从而实现较好的滤波性能;若高维测量中每个测量分量可以完整的感知与测量目标系统状态时,则相比于单一测量分量实现的状态估计,采用轮询协议下的状态估计实现滤波性能的折中.

例2考虑一类机动目标跟踪系统并采用如下恒定加速度运动模型[29]:

其中:dt是采样周期,状态向量x1(k),x2(k)和x3(k)分别代表机动目标位置,速度以及加速度.采样周期dt0.05 s;噪声输入w(k)N(0,0.1);外部干扰输入为v(k)N(0,0.5);其它系统参数B[0 0 0]T,M[1 0 0].

该系统由4个滤波器组成的分布式滤波网络观测,目标系统的位置信息可由雷达测量得到,因此测量方程(4)的参数选择如下:

如图8所示,假设滤波器网络具有3种时变的通信拓扑,拓扑切换概率矩阵Π(k)由以下3个概率矩阵组成:

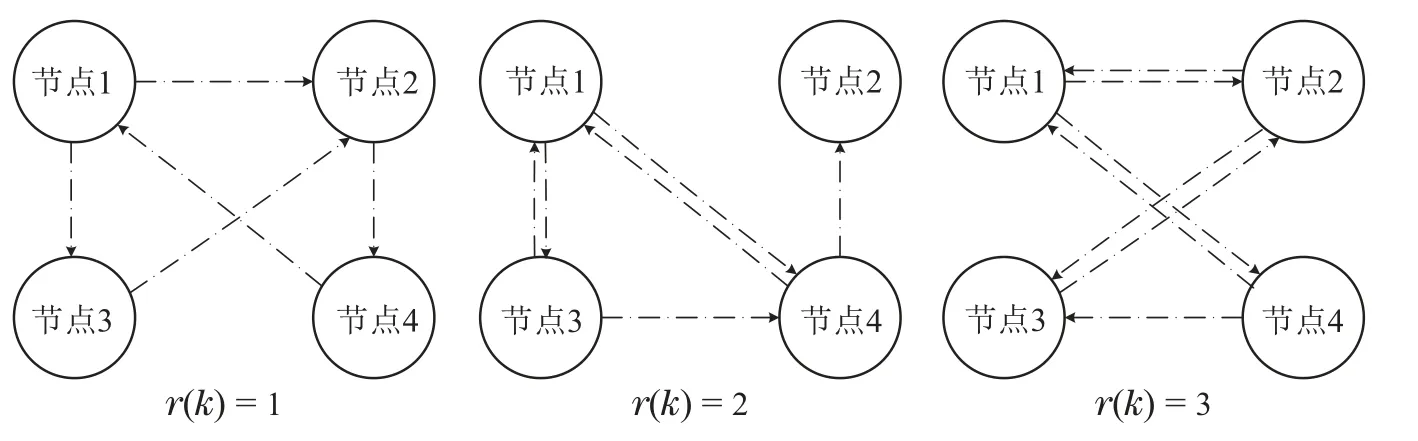
图8 滤波器网络通信拓扑Fig.8 Filtering network communication topologies

假设系统的初始状态和滤波器的初始状态均为零;初始的通信拓扑r(0)2,增广滤波误差系统衰减速率0.92.

仿真结果如图9-13所示.图9展示了一种可能的网络拓扑切换顺序;图10中红色线、绿色线以及蓝色线分别代表测量分量1,2,3激活情况,可以看出每个节点的测量分量在轮询通信协议作用下拥有平等的机会访问网络;图11对比了目标系统真实的运动轨迹z(k)(即x1(k)),滤波网络各个节点估计的运动位移估计(k)(即(k)),以及直接通过雷达测量的运动轨迹yi(k),其中yi(k)数据来自每一时刻被传输的最新数据.可以看出,雷达测量的目标系统运动轨迹相比于分布式滤波器估计的运动轨迹,产生了一定幅度的抖动,这是由于环境噪声对雷达测量结果产生了干扰.图12给出了滤波节点的估计误差曲线(k),i1,2,3,4,滤波网络整体估计误差曲线˜z(k)以及输出估计误差渐近上界/(1-)12.5.

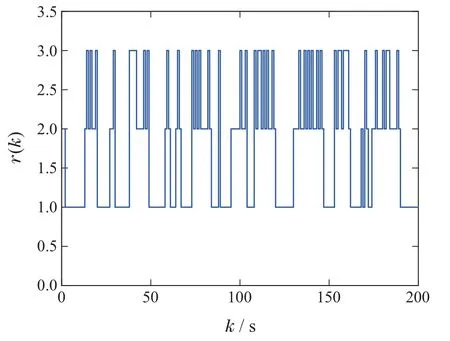
图9 非齐次Markov链Fig.9 Nonhomogeneous Markov chain

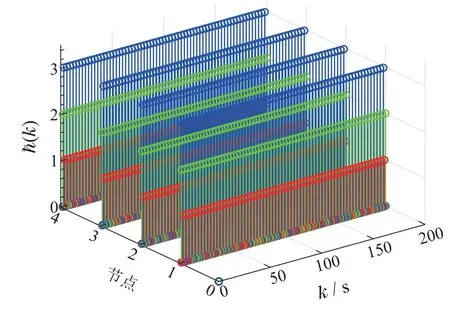
图10 轮询协议下每个节点测量分量活动情况Fig.10 Periodic activation of node measurement components under Round-Robin protocol

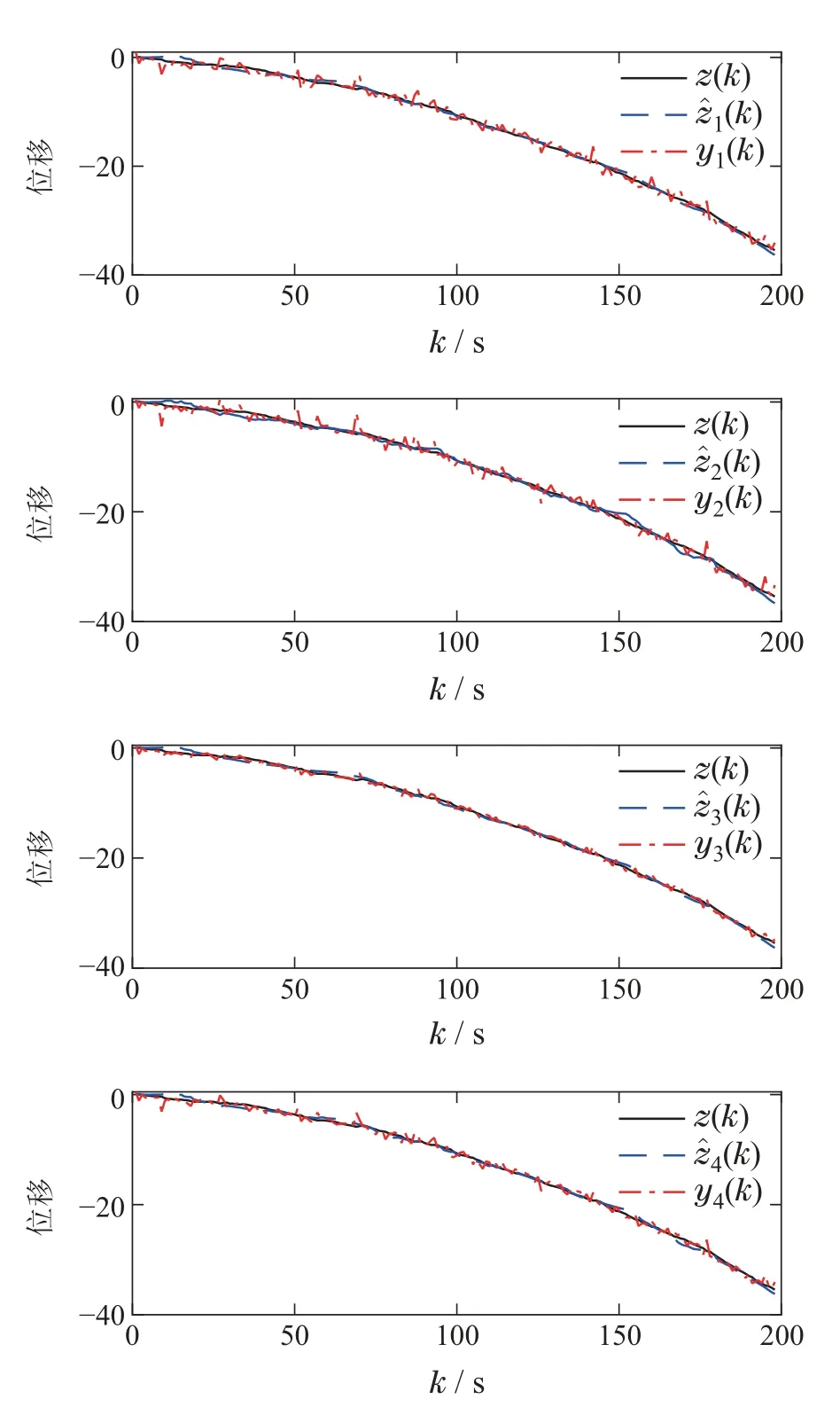
图11 系统实际输出z(k),估计的输出(k)以及测量值yi(k),i1,2,3,4Fig.11 Actual system output z(k),estimated output(k),and measurement yi(k),i1,2,3,4

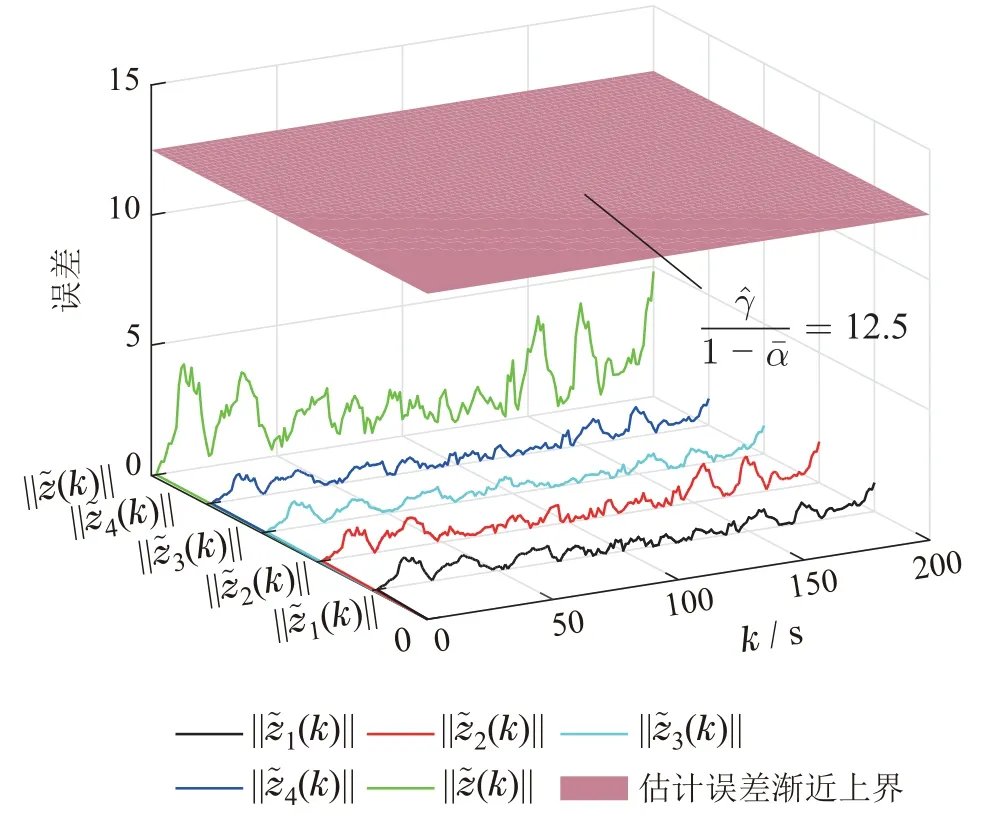
图12 滤波网络估计误差Fig.12 Estimation error of the filtering network

图13对比了滤波网络估计误差曲线和基于雷达测量的估计误差曲线.通过计算可以得到此情况下分布式滤波网络的平均输出误差为

基于雷达的测量数据与真实位移之间的平均误差为

图13 估计误差与测量误差对比Fig.13 Estimation error versus measurement error

仿真结果显示,所设计的分布式状态估计器对外部噪声和干扰具有一定的鲁棒性,并且实现期望的系统轨迹估计.

6 结论

本文讨论了一类基于传感器网络的信息物理系统分布式状态估计问题.为传感器网络引入了轮询通信协议,避免了数据拥塞和充分利用了有限带宽资源.采用非齐次Markov链描述了分布式滤波器网络随机时变的通信拓扑.构建了理想的分布式滤波方案,利用线性矩阵不等式方法给出了增广滤波误差系统在均方意义下最终有界的充分条件.进一步地,将分布式滤波器存在问题转化为一个凸优化问题,所得到的分布式滤波器增益实现了输出估计误差的渐近上界最小.最后,通过两个数值仿真验证了本文所提分布式滤波方法的有效性.