编解码和时延约束下的网络控制系统最优跟踪性能

张斌 姜晓伟 陈向勇张先鹤

(1.中国地质大学(武汉)自动化学院,湖北武汉 430074;2.工业物联网与网络化控制教育部重点实验室,重庆 400065;3.复杂系统先进控制与智能自动化湖北省重点实验室,湖北武汉 430074;4.地球探测智能化技术教育部工程研究中心,湖北武汉 430074;5.临沂大学自动化与电气工程学院,山东临沂 276000;6.湖北师范大学电气工程与自动化学院,湖北黄石 435002)

1 引言

由于计算机技术、控制技术和通信技术的深度融合,网络化控制系统也因此吸引了大量国内外专家学者的注意力[1-5].最优跟踪是目前网络控制系统领域中研究较多的问题之一[6-7].众所周知,通常最小的跟踪误差取决于被控对象的非最小相位零点和不稳定极点[8].这些结果是基于传统的假设,即控制器和被控对象以理想的方式进行信息交流而得到的.近年来,人们对发生非理想数据传输的控制系统的研究越来越感兴趣,如研究在时延、丢包、信道噪声等通信约束条件下网络控制系统的跟踪性能极限,经过大量专家学者的不懈努力,已经取得了非常丰硕的成果,例如,文献[9]研究了离散时间、MIMO线性定常系统的最优跟踪性能和调节性能.文献[10]研究了加性白噪声信道下的多输入多输出网络反馈系统的稳定性和跟踪性能.文献[11]基于双自由度控制器分别研究了在前馈信道和反馈信道中具有量化和丢包约束的MIMO网络控制系统的输出跟踪控制问题.文献[12]研究了具有丢包和信道噪声的SISO离散时间网络控制系统的最优跟踪性能.从上述文献可知,网络控制系统的最优跟踪性能与被控对象的本质特征和通讯信道中的各种网络约束密切相关,因此,基于通讯约束对于网络控制系统的性能限制的研究是非常有必要的.

众所周知,网络控制系统中的时延和丢包是影响系统稳定性和性能的主要因素,严重时,甚至导致系统不稳定,而编码器和解码器的引入在一定程度上可以提高网络控制系统的性能,因其在信号传输前对其进行编码,在信号传输后对其解码,可以有效地防止数据在传输过程中发生的信号失真或者错误.因此本文在由信道输入能量和系统跟踪误差能量的权衡构造的跟踪性能指标的基础上综合研究了在时延、丢包、编码器和解码器以及双通道加性高斯白噪声影响下的最优跟踪性能,在网络信道构造方面,本文较以往所建立的网络控制系统更接近于实际情况,功能性更强.

MIMO系统较SISO系统使用多个发射器和接收器来同时传输更多数据,传输速率和通信质量更高,则针对上述通讯约束,研究MIMO系统的最优跟踪性能更具有实际意义.因此,本文的主要贡献有以下3个方面:首先通过提出SDOF控制方案,本文建立了MIMO系统在多约束影响下的最优跟踪控制性能的新框架;其次给出了编解码和其他约束条件对最优跟踪性能影响的表达式;最后基于频域分析方法和Youla参数化等方法得到了一个精确的表达式,揭示了系统跟踪性能与被控对象的非最小相位零点和不稳定极点(包括位置和方向)以及网络通信特征密切相关.

本文组织如下:第2节中介绍相关定理,第3节推导了具有多约束的网络控制系统的跟踪性能极限,第4节通过一个典型例子来说明文中所得到的结果,第5部分给出了本文的结论和未来的研究方向.

2 问题描述

考虑如图1所示的在前向通道中存在噪声约束和反馈通道中存在噪声约束、丢包约束以及时延约束的离散时间MIMO网络控制系统,G表示被控对象,K表示单自由度控制器,其z变换分别为G(z)与K(z),r表示系统参考输入,n1表示前向通道中的加性高斯白噪声,n2表示反馈通道中的加性高斯白噪声,y表示系统输出,u表示控制输入,其z变换分别为和RH∞表示稳定的、正则的、实有理传递函数(矩阵)集合.通信信道由4个参数表征:双通道噪声n1与n2、丢包dr、时延z-τ和编码器和解码器(假设其为非最小相位的)分别为A,A-1,参数dr表示数据包是否被丢弃.

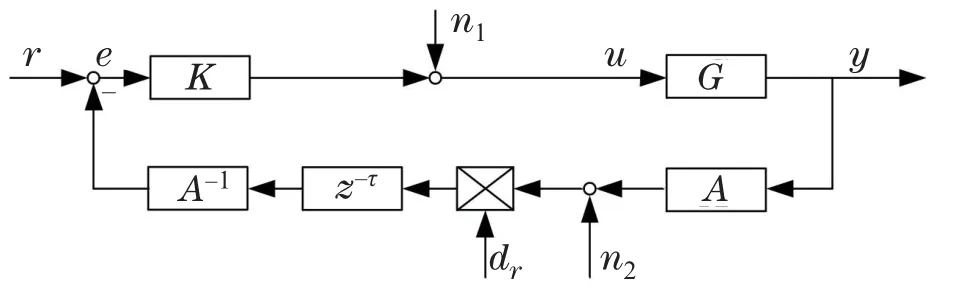
图1 多通信约束的单自由度控制系统Fig.1 SDOF control system with multiple communication constraints

其中:P{dr(k)0}q,P{dr(k)1}1-q,q为数据包丢包概率.参考输入r是阶跃信号的矢量形式,

其中:v为常数酉向量,n1,n2分别表示前向通道和反馈通道的加性高斯白噪声,对于信道i(i1,2,...,m),其功率谱密度分别为并假设上述信号是相互独立的.定义误差信号以及系统的跟踪性能指标为

其中:Γ为预先给定的信道输入能量的约束值,且,λ是跟踪误差与信道输入能量约束之间的权衡因子,由此,本文研究的问题为:在所有使得系统稳定的控制器集合中,设计出一个能使得式(3)的性能指标函数取得最小值的最优控制器,即

其中κ表示所有稳定的控制器集合.对于有理传递函数矩阵(1-q)G,设它的互质分解为如下形式:

这里N(z),M(z),˜M(z),˜N(z)H∞,并且满足双Bezout等式

所有能使得多输入多输出系统稳定的控制器K都属于这样的一个集合κ

其中Q是自由设计的参数矩阵,对应不同的控制器.假设被控对象P是右可逆的.存在如下形式的左右互质分解:

其中:Lz,Bp和Az为全通因子,Nm,Mm和Om为最小相位因子,Lz包含了被控对象所有的非最小相位零点,Bp包含了被控对象所有的不稳定极点,Az包含了编码器所有的非最小相位零点,并且全通因子Lz和Bp可以分解为以下形式:

3 最优性能分析

由图1可得

则有

其中:

由式(4)-(6)可得

则由式(3)(9)-(13)得

其中:Vdiag{β1,β2,...,βn},Wdiag{γ1,γ2,...,γn}.

定理1考虑如图1所示的网络控制系统,假设被控对象有不稳定极点pi,i1,2,...,Np,其极点方向为ηi;非最小相位零点si,i1,2,...,Nz,其零点方向为ωi,并且参考输入和性能指标如定义式(1)和(3)所示,那么该系统的跟踪性能极限为

其中:

为了计算J*,做出如下定义:

显而易见,可以选择一个合适的Q使得

则

由柯西定理,有

则

证毕.

4 数值仿真

本节给出了一个仿真实例来证明该方法的准确性.考虑离散多输入多输出被控对象,其传递函数矩阵为

在给定的被控对象中,含有一个非最小相位零点zk(|k|＞1),其输出零点方向为ω(1 0)T,被控对象含有不稳定极点p2,其极点方向为η(0 1)T,定义输入向量为

选择

有

当τ分别为0.2,0.5和0.8时,多输入多输出离散网络控制系统的跟踪性能极限如图2所示,从图2可以看出,多输入多输出网络控制系统反馈通道中时延参数越大,离散多输入多输出网络控制系统的性能越差,从图2中还可以看出,当被控对象的非最小零点和不稳定极点充分接近时,离散多输入多输出网络控制系统的跟踪性能会急剧恶化.从图3中可以看出,随着分组丢失概率的增加,跟踪性能变得更差.

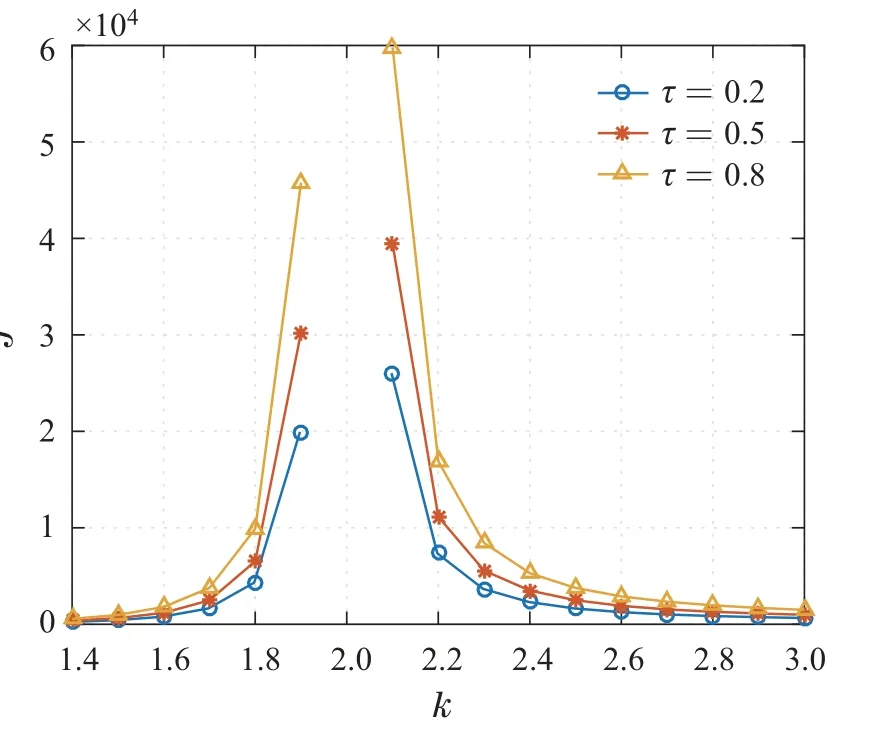
图2 不同时延下的跟踪性能极限Fig.2 Tracking performance limits with different time delays

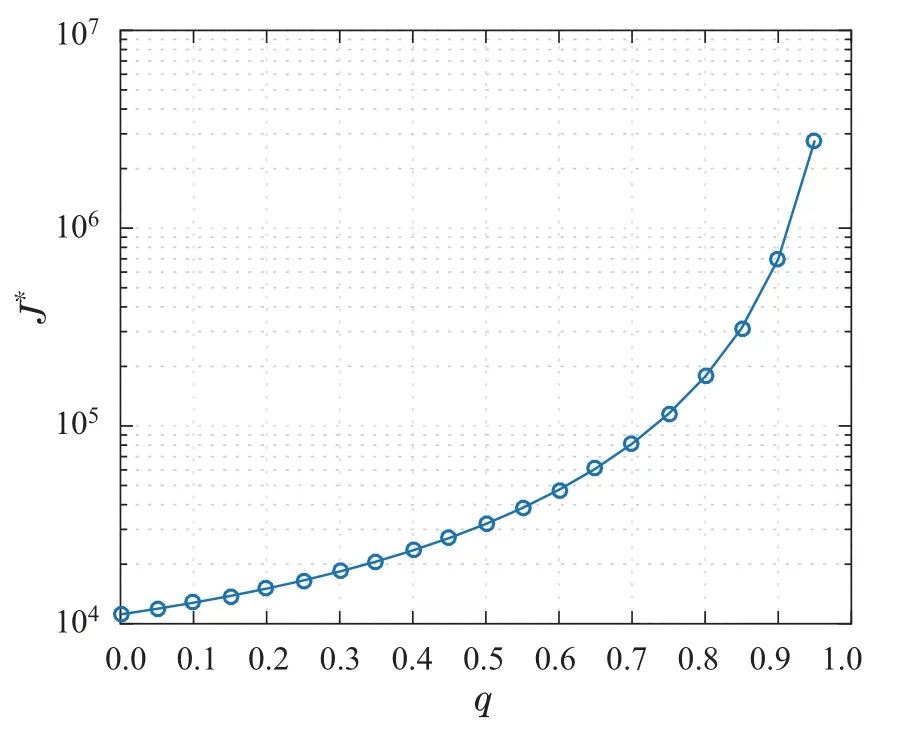
图3 数据包丢失的概率qFig.3 The probability of packet loss q

5 结论

本文研究了在信道输入功率约束下,具有丢包、时延和双通道噪声的最优跟踪性能问题.考虑网络中的限制是分组丢失、双通道噪声、时延以及编码和解码.通过采用单自由度控制器结构,并且借助全通分解和互质分解等工具推导得到了该系统最优跟踪性能的显式表达式.结果表明,最优跟踪性能可以用两部分之和来描述,一部分依赖于给定对象的非最小相位零点和参考输入信号,另一部分依赖于给定对象的非最小相位零点和不稳定极点,以及丢包率、信道噪声、时延和编解码.结果表明,通信信道的丢包概率、时延和信道噪声会从根本上制约控制系统的跟踪能力.这项工作未来可能的扩展研究包括更一般的网络控制系统配置,如前馈和反馈路径中的非理想通信信道,以及更一般的信道模型,如带宽有限、信噪比约束的通信信道,并可将其推广网络控制系统中被控对象包含多重零极点的情况中去.