高灵敏度微位移零差干涉方法

翟中生，张 艺，冯 维，冯 胜，王选择，熊 芝

（湖北工业大学 机械工程学院 现代制造质量工程湖北省重点实验室，湖北 武汉 430068）

引言

在众多测量技术中，白光干涉技术测量精度高、视野大、可溯源[1-3]，被广泛应用于光学元件面形测量、微弱目标探测、微小位移测量等领域[4-7]。白光干涉的测量精度主要取决于测量光程差的大小，由于白光的零光程对位置非常敏感，因此能够实现精密测量[8-10]。为了实现更高性能的白光干涉技术，其零光程差位置的确定极其重要[11-12]，因此，需要对零光程差进行更准确的定位[13-15]。

为了准确判定零光程差的位置和提高干涉测量的精度，许多学者为此做了很多研究。徐勇祥等人运用空间频域算法对台阶样品进行三位形貌测量[16]，能够消除高阶色散的影响，但存在因最小二乘拟合和傅里叶变换引起的运算量过大的问题；沈明兴等人提出一种9～11 步相移算法，用于改善干涉测量中深度受限的问题[17]，其算法能够获得优良的线性度，并能有效提高相位的准确性，但同样存在因最小二乘拟合及相位展开导致的运算量较大的问题；Pavlicek P 等人针对噪声在提取干涉图包络曲线中的影响，提出一种希尔伯特变换包络检测的方法[18]，能够有效减少噪声对包络线提取的干扰作用；Ma S 等人提出一种新型的干涉图包络曲线提取方法，利用傅里叶变换技术补偿零光程差位置[19]，该方法虽然精度较高、抗干扰能力强，但同样存在耗时长、运算量大等问题。

为了解决以上问题，准确定位白光干涉的零光程差位置，并最大限度地降低干扰因素对实验结果的影响，设计了一种新型的零差干涉测量系统。该系统对迈克尔逊干涉仪的光路进行改进与完善，通过白光干涉条纹的强度公式和波动原理分别对白光信号和激光信号进行分析，将激光二次干涉的零点与白光干涉的暗纹定位，使其在零光程差时达到斜率最大值，从而改善系统的灵敏度。

本文所述的基于白光干涉和激光二次干涉相结合的高灵敏度微位移零差干涉方法主要创新点为：1）利用白光光谱宽、相干长度短的特点，与激光二次干涉（零差探测）相结合，通过激光二次干涉的零位锁定白光干涉的暗条纹，灵敏度相较于单独激光二次干涉至少提高1 832 倍。2）激光二次干涉对激光一次干涉进行零差探测，激光干涉信号表现为正弦或余弦形式，零光程差处信号灵敏度明显提高，起到了零差探测的作用。

1 原理设计与信号分析

1.1 整体测量原理设计

实验整体光路图如图1所示。结合白光零差干涉和激光二次干涉，并根据使用光源的不同，测量过程主要分为2 步：

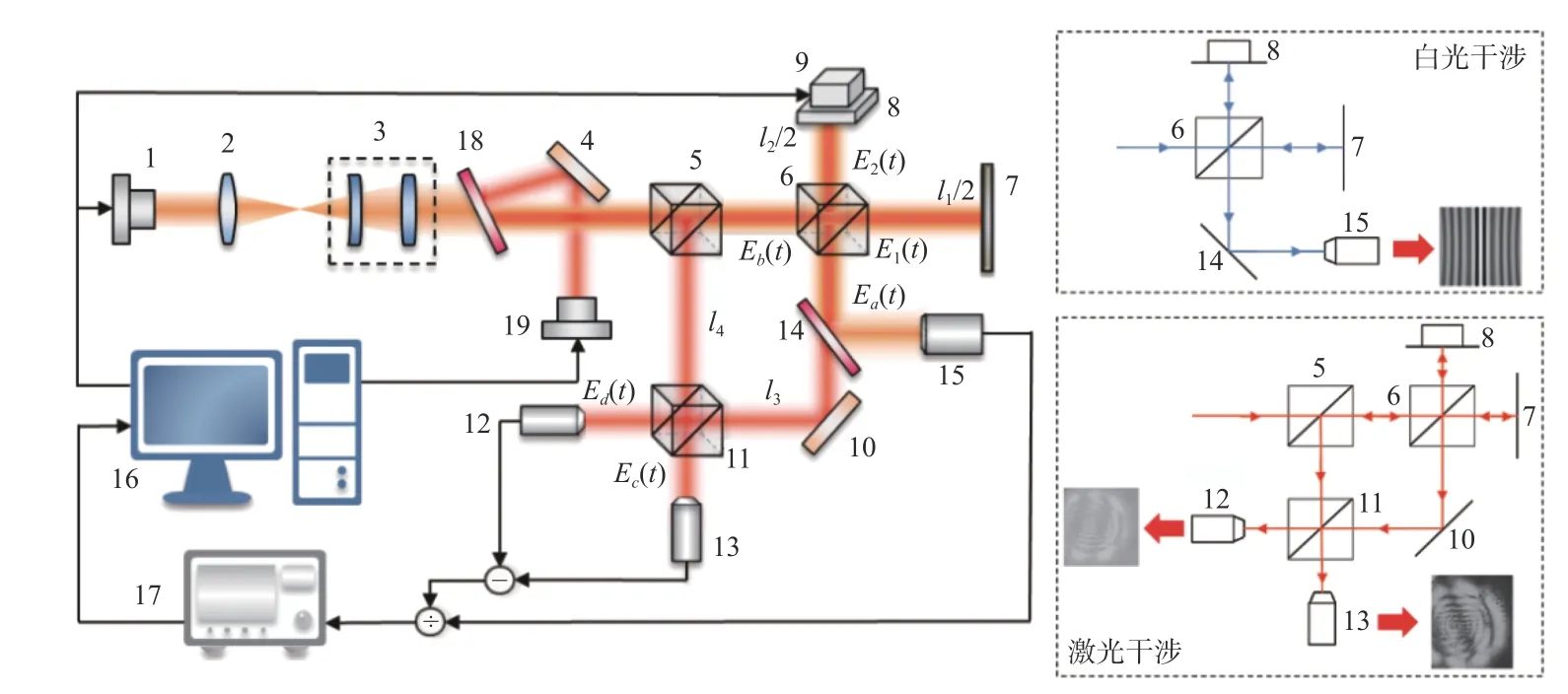
图1 测量原理图Fig.1 Schematic diagram of measuring system

第1 步，关闭激光光源19，打开白光光源1。白光光束经过消色差透镜2 后汇聚，经过准直模块3 后出射为平行光；该平行光经过第2 分光棱镜6 后发生透射和折射，透射光入射进参考镜7、反射光照射被测物8 后，均被反射回第2 分光棱镜6，形成一级干涉；设参考镜7 和被测物8 到第2 分光棱镜6 距离的2 倍分别为l1和l2，调整l1和l2的大小，使其在零光程差位置为暗条纹。利用分束镜14 使白光干涉信号入射进第3 探测器15，并检测白光信号。

第2 步，关闭白光光源1，打开激光光源19。激光束先后经过反射镜4 和分束镜18 后与白光同轴共路，在第2 分光棱镜6 处形成一次干涉；干涉后的2 路信号分别经过反射镜10 和第1 分光棱镜5，在第3 分光棱镜11 处形成二次干涉，反射镜10 到第3 分光棱镜11 的距离为l3，第1 分光棱镜5 到第3 分光棱镜11 的距离为l4；一次和二次干涉信号分别由光电探测器12 和13 检测，并对其进行减法运算。

通过上述步骤后，即可得到白光干涉和激光二次干涉信号，将2 路信号做除法处理，计算处理后信号的灵敏度，即所述零差干涉测量系统的灵敏度，并与激光二次干涉的灵敏度进行对比。

1.2 白光干涉信号分析

不同的光源照射会产生不同的效果，干涉条纹的光强在单色光照射下可表示为

式中：λ代表单色光波长；I0代表背景光强；x为理想光与被测光的光程差，其光强交变成分为

白光光源包含了整个可见光谱的成分，自红色到紫色，具有较宽的光谱宽度和较短的相干长度，相当于多种单色光的叠加。干涉条纹的强度交变成分如（3）式所示[20]。

式中：L代表相干长度，满足L=λ2/Δλ；λ为中心波长；Δλ表示光谱半峰值宽度。

1.3 激光干涉信号分析

根据波动原理和琼斯矩阵，假设原矢量波为E0，则第2 分光棱镜6 后出射的矢量波E1和E2可表示为

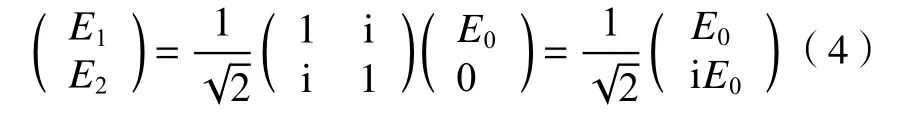
式中：i 为复数的虚部。

矢量波E1和E2分别经过参考镜7 和被测物8，并被反射回第2 分光棱镜6，得到2 束干涉矢量波Ea和Eb，见图1所示，表达式为

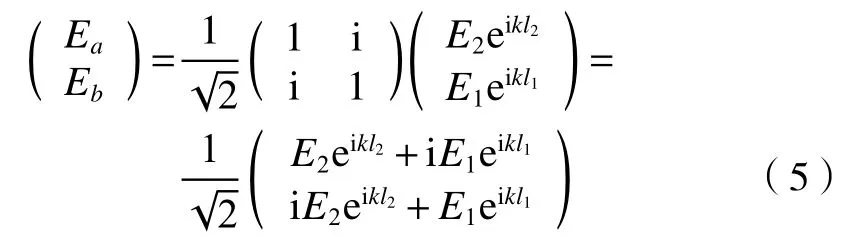
一次干涉后形成的2 路干涉矢量波Ea和Eb的光强差可表示为

随后，一次干涉后的信号分别通过第1 分光棱镜5 和反射镜10，到达第3 分光棱镜11，得到Ec和Ed。

调整光路使l3和l4满足

式中：l1−l2=x；Ic−Id表示激光二次干涉后2 路干涉信号Ec和Ed的光强差。（8）式可改写为

1.4 灵敏度分析

白光干涉主要通过寻找零光程点测量高度信息，在零光程时，即x=0 干涉信号最强，此时的灵敏度可表示为

当x=0 时，对应于干涉信号中cos(2πx/λ)的峰值点，斜率变化最缓慢（S1=0），但同时由于噪声的影响，实际的零光程点不易找准，灵敏度并不高。

对激光而言，由（6）式和（9）式可知，激光干涉信号为正弦或余弦的形式。以（9）式为例，激光二次干涉信号随光程差变化的灵敏度为

当光程差为零（x=0）或整数倍波长时（x=nλ），二次干涉灵敏度达到最大值(2πI0/λ)。

为了实现更高灵敏度的高度测量，结合（3）式的白光和（9）式激光干涉信号，提出将两者相结合的灵敏度计算方法，如下式：

由上式可知，当光程差x=0 时，分子达到峰值k，而分母为0，因此灵敏度S3在x=0 处为无穷大，相较于S1和S2灵敏度更高。

2 仿真实验结果分析

为了考察设计的系统是否拥有较快的响应速度，采用灵敏度对系统进行分析。为研究光程差与光强变化之间的关系，本文将3 种灵敏度S1、S2、S3进行对比。

仿真实验采用的光源具体参数如下：平均波长λ0为560 nm，平均光强为100 lux，对比度为0.25，相干长度L为1 000 nm。白光干涉S1 和激光二次干涉S2 灵敏度曲线如图2所示，图3所示为激光二次干涉灵敏度/白光干涉灵敏度结果，即S3曲线。

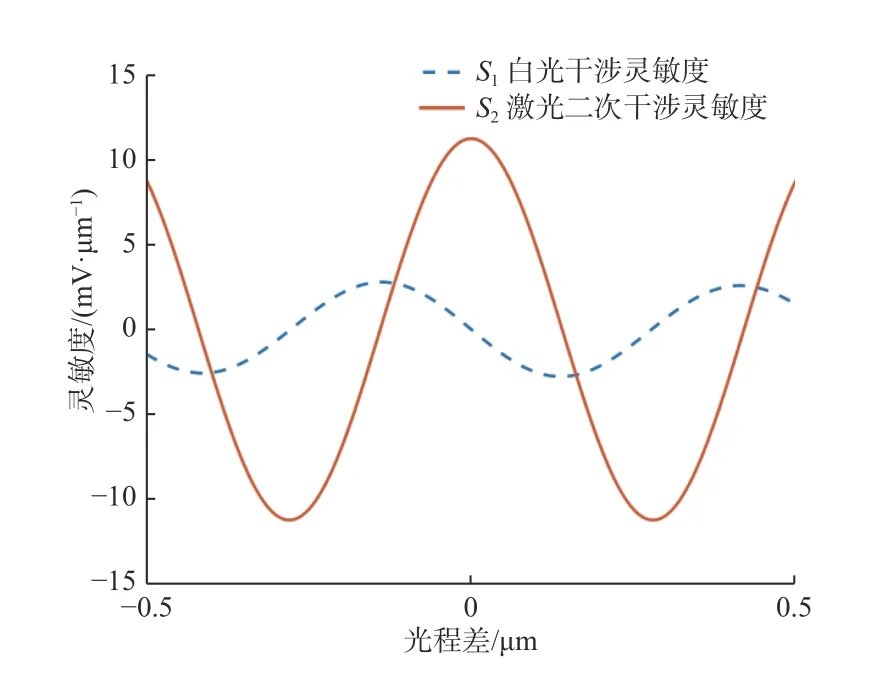
图2 白光和激光二次干涉灵敏度Fig.2 Sensitivity of white light and laser secondary interference

图3 灵敏度S3 曲线Fig.3 Sensitivity S3 curves

由图2 可知，当光程差x=0 时，白光干涉信号斜率为0，即其灵敏度为0；而激光二次干涉信号的斜率在此时达到最大值，即S2灵敏度曲线达到峰值。由图3 可知，光程差x=0 时，激光二次干涉灵敏度/白光干涉灵敏度S3的值趋近于无穷大。这表明在零光程差点，激光二次干涉/白光干涉信号灵敏度明显高于单独激光二次干涉，即本文所述零差干涉系统具有更高的灵敏度。

3 实验实物结果分析

3.1 实验搭建

首先搭建迈克尔逊干涉实验装置，实验装置图如图4所示，可分为光路部分和探测器采集部分。其中光路部分分为5 个模块：白光光源、准直、激光光源、一次干涉和激光二次干涉模块；探测器采集分为2 个模块：白光采集模块和激光采集模块。其中白光光源选用白光LED，型号为大恒GCI-060411，波长范围为440 nm～670 nm。压电陶瓷镜型号为Thorlabs 公司的PK4DMP2，分光棱镜为BS010，探测器选用LSSPD-1.2。

图4 实验装置图Fig.4 Experimental device diagram

白光调试之前，借助激光、调整镜架使得一次干涉模块的光程差相等。在此基础上，调整激光条纹使其只产生一个干涉条纹，关闭激光光源，打开白光光源，对二维平移台进行微调，产生彩色条纹，即零级干涉条纹。

调试激光二次干涉时，一次干涉产生的2 路干涉信号分别经过反射镜10 和第1 分光镜5，通过计算机控制PZT 驱动来形成光程差，在第3 分光镜11 处产生二次干涉，且使其零位斜率为最大值，从而提高干涉测量的灵敏度。

3.2 数据处理与综合分析

首先，通过信号源向PZT 输入三角波信号，PZT 运动使光路中的光程差发生改变，随之可用示波器观察到干涉条纹产生明显变化，分别用白光探测器和激光探测器采集白光干涉和激光二次干涉信号。

数据采集时，设置采样频率为20 Hz，压电陶瓷每移动1 μm，采样1 400 个采样点。激光二次干涉和白光干涉原始数据如图5 和图6所示，横坐标表示运动位移（μm），纵坐标表示电压值（mV）。

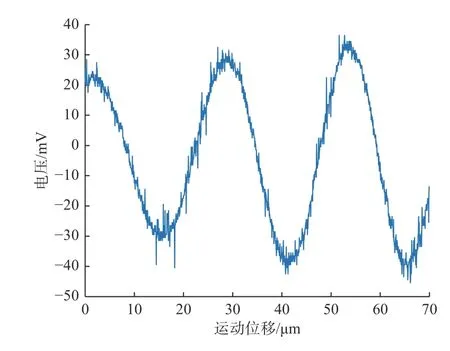
图5 激光干涉信号原始数据Fig.5 Original data of laser interference signal

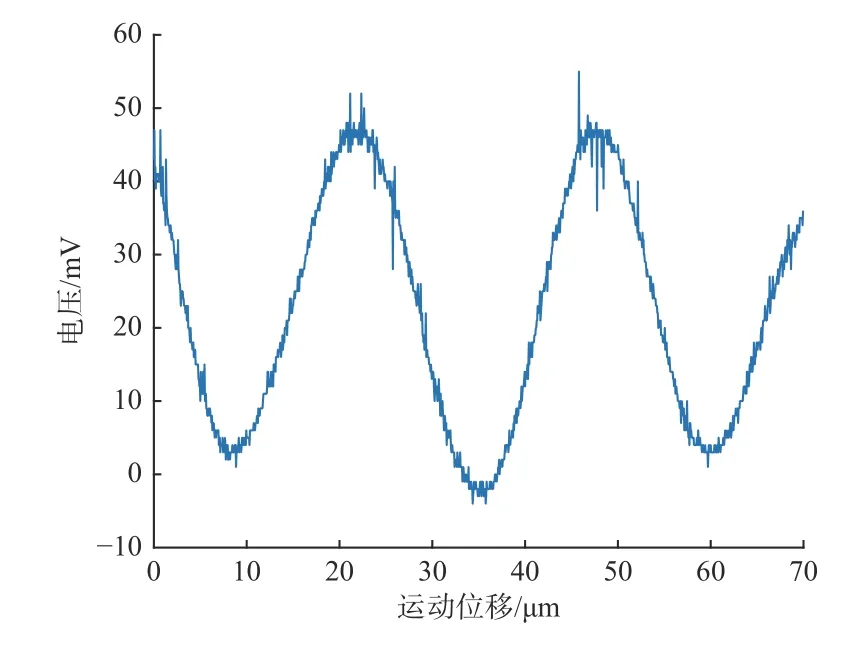
图6 白光干涉信号原始数据Fig.6 Original data of white light interference signal

随后进行低通滤波处理，去除高频信号，保留低频信号，并进行曲线拟合，如图7 和图8所示，得到激光二次干涉和白光干涉信号拟合曲线。

图7 激光二次干涉信号曲线拟合Fig.7 Curve fitting of laser secondary interference signal

图8 白光干涉信号曲线拟合Fig.8 Curve fitting of white light interference signal

最后对白光干涉和激光二次干涉拟合曲线进行灵敏度分析，即对拟合曲线进行求导，并得到其斜率最大值，如图9所示。由图9 可知，当运动位移为2.612 μm 时，白光干涉信号灵敏度曲线达到峰值7.018；当运动位移为59.65 μm 时，激光二次干涉信号灵敏度曲线达到最大值9.497。

图9 白光干涉和激光二次干涉灵敏度曲线Fig.9 Sensitivity curves of white light interference and laser secondary interference

将激光二次干涉灵敏度与白光干涉灵敏度曲线相除，得到零差干涉系统灵敏度曲线S3，如图10所示。由图10 可知，零差干涉系统灵敏度在运动位移x=59.85 μm 时达到峰值17 400，远远超出激光二次干涉信号的灵敏度。

图10 零差干涉系统灵敏度Fig.10 Sensitivity of homodyne interference system

将零差干涉系统灵敏度与激光二次干涉信号灵敏度进行对比，有：

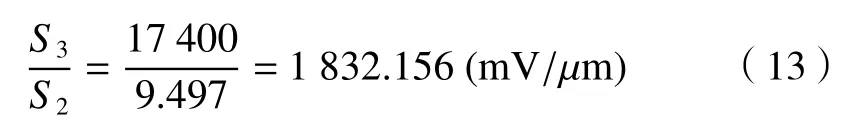
随后，考察测量结果的不确定度。由于本实验采集的激光及白光信号是随运动位移变化的，无法进行重复测量，因而只考虑噪声信号对实验结果的影响，即用其他非统计方法评定的B类分量。

如图11所示为实验测得的噪声信号，其范围为±0.5 mV。只有当噪声足够小时，才能利用位移驱动形成干涉信号，因此该噪声范围就是系统能够产生干涉信号的最小驱动位移，即系统的误差限。假设所述零差干涉系统误差服从均匀分布，则系统不确定度为

图11 噪声分析Fig.11 Noise analysis

4 结论

本文针对如何准确定位白光干涉中零光程差位置和现有干涉测量中运算量较大的问题，提出了一种将白光干涉和激光二次干涉相结合的零差干涉测量系统。首先分别对干涉信号进行信号分析，计算白光干涉和激光二次干涉条纹的强度交变成分及其相应的灵敏度，然后提出新的灵敏度计算方法，即将激光二次干涉灵敏度与白光干涉灵敏度相除，并对其进行仿真模拟。最后，搭建零差干涉测量系统实验光路，利用激光二次干涉的零点准确定位白光干涉的暗纹，即零光程差位置，并进行数据采集。实验结果表明，本文所述零差干涉测量方法比激光二次干涉的灵敏度至少提高1 832 倍，相应的测量不确定度仅为±0.288 7 mV，相比传统干涉测量方法具有计算量小、灵敏度高的优点。