面向大型新能源基地小干扰稳定性提升的调相机选址方法

王 康，李子恒，杨超然，李 琦，刘晨曦，辛焕海

（1. 国网陕西省电力有限公司，陕西省西安市 710048；2. 国网湖北省电力有限公司，湖北省武汉市 430072；3. 浙江大学电气工程学院，浙江省杭州市 310027）

0 引言

随着能源转型工作的推进，风电、光伏等新能源发电和高压直流输电在电力系统中的占比逐年增加［1-2］，电网演变为含高比例可再生能源和高比例电力电子设备的新形态［3-5］。在这一形态下，电网表现出低短路比特征，电网电压支撑能力相对变弱，给电力系统的安全稳定运行带来极大挑战［6-7］。因此，对于大规模新能源馈入的电力系统，通常需要加装无功补偿装置来提高电压维持能力和提升电网强度。

电力系统中广泛采用的动态无功补偿装置主要有静止无功补偿器（SVC）、静止同步补偿器（STATCOM）和 同 步 调 相 机 等。 SVC 和STATCOM 具有高可控性，常被用于为新能源场站提供无功补偿；但现有研究表明，SVC、STATCOM与新能源设备之间可能产生较强耦合作用，导致系统存在振荡风险［8-10］。不同于SVC 和STATCOM，调相机具有无功输出受系统电压影响小、可提升电网强度等优点。目前针对调相机的研究，主要集中在高压直流输电系统中接入调相机后对换相失败抑制作用的研究［11-16］。文献［11-12］研究指出安装调相机后提高了直流系统的电压稳定性并降低了换相失败的概率；文献［13-14］根据调相机对多馈入直流系统中换相失败的抑制效果提出了调相机的最优选址方案；文献［15］比较了新一代调相机与SVC、STATCOM 这类基于电力电子技术的无功补偿装置之间的差异，说明了调相机具有更优秀的动态电压支撑能力。此外，调相机具有机械旋转部件，还可以为系统提供惯性支撑、改善系统频率响应特性［16］。然而，目前关于调相机在电网中的应用研究多集中于对直流送受端电网强度的提升，而鲜有研究关注调相机对新能源基地电网强度的影响规律。

调相机对送受端电网强度的提升主要聚焦于静态或暂态电压稳定问题，而目前新能源基地还面临着振荡问题，后者稳定机理有所不同，理论研究还不完善。为此，亟须探究在新能源基地安装调相机后系统电网强度的量化方法与提升机理。需要说明的是，广 义 短 路 比（generalized short-circuit ratio，gSCR）［4］是一种可用于刻画多馈入系统电网强度和稳定裕度的指标。本文将以gSCR 指标为基础，探究调相机接入对新能源场站电网强度和稳定裕度的作用机理。

本文从小干扰稳定性的角度出发，解析了调相机接入多馈入系统后对系统稳定性的影响。首先，建立了含调相机的电力电子多馈入系统的动态模型。其次，从理论上论证了安装调相机等效于增大了多馈入系统的gSCR 指标，从而可提高系统的电网强度并增大系统的稳定裕度。在此基础上，建立了考虑多调相机选址问题的优化模型和算法，该算法以最大化提升gSCR 为目标，进而可实现最大化提升大规模新能源系统电网强度和稳定裕度的目的。

1 含调相机的多馈入系统建模

本章在频域中建立新能源、调相机和电网的小扰动动态模型。

1.1 新能源设备的导纳模型

新能源设备通常以电压源型变流器（VSC）作为功率接口接入交流电网，单机新能源设备并网电路图及其控制框图见图1，VSC 采用基于锁相环（PLL）的矢量控制策略。图中:Pdc和Vdc分别为直流输出功率及电压；Cdc为直流侧电容；Iabc和Vabc分别为三相电流和电压；PWM 表示脉宽调制。

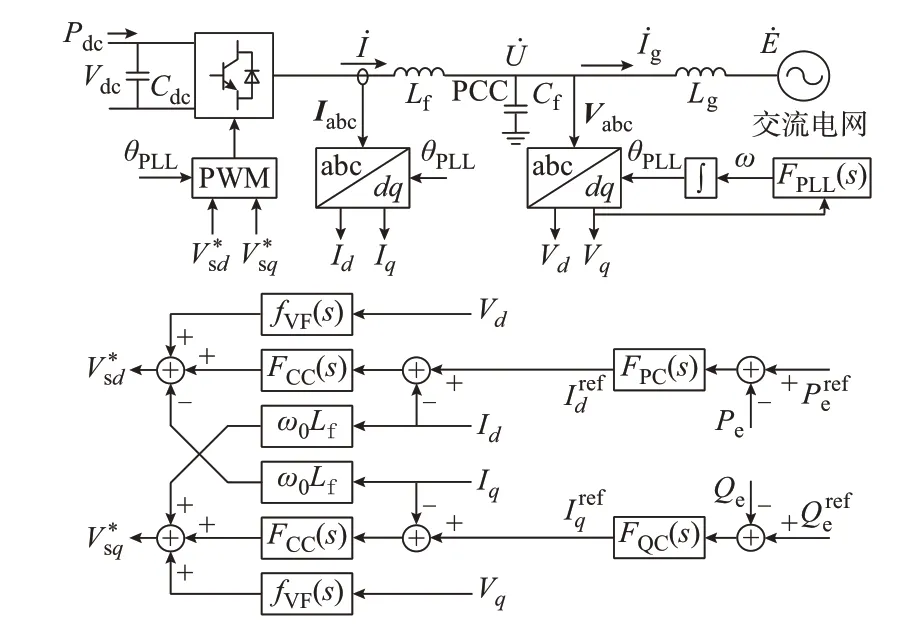
图1 新能源设备控制框图Fig.1 Block diagram of control for renewable energy equipment

利用复系数传递函数［17］，在VSC 自身的dq控制坐标系下，LCL 滤波器的动态方程可以表示为:

与电流环串级的功率外环用于实现功率的控制，其动态方程可表示为:

式中:FPC(s)=KPCP+KPCI/s为有功外环控制器的传递函数，其中，KPCP和KPCI分别为有功外环的比例和积分系数；FQC(s)=KQCP+KQCI/s为无功外环控制器的传递函数，其中，KQCP和KQCI分别为无功外环的比例和积分系数；Pe和Prefe分别为VSC 输出的有功功率及其参考值；Qe和Qrefe分别为VSC 输出的无功功率及其参考值。

VSC 输出的有功功率Pe和无功功率Qe可通过式（6）计算。

变流器通过PLL 检测交流电网相位实现同步运行，PLL 的动态方程为:

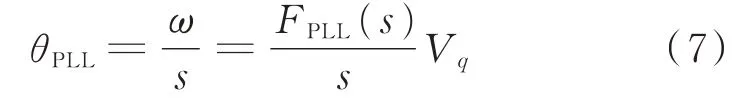
式中:FPLL(s)=KPLLP+KPLLI/s为PLL 的传递函数，其中，KPLLP和KPLLI分别为PLL 的比例和积分系数；θPLL为dq控制坐标的角度。

式（1）—式（7）为dq控制坐标系下的VSC 方程。为分析整个系统的稳定性，需根据式（8）将VSC 端口电压和电流变换到全局xy坐标下，即

线性化式（1）—式（8）可以得到用于分析新能源设备并网小干扰稳定性的频域导纳模型（具体推导过程可参考文献［18］）。

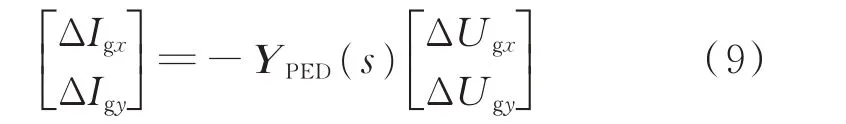
式中:Δ 表示各对应变量的扰动量，下同；YPED(s)为导纳矩阵。

1.2 调相机原理及导纳模型

同步调相机实质上是在空载状态下运行的同步电机，通过励磁系统控制其向系统发出或吸收无功功率来维持端电压的恒定。

同步调相机的数学模型与同步发电机相似，绕组的基本方程为［19］:

与同步发电机类似，调相机转子摇摆方程如下。

式中:Te为调相机的电磁转矩；Tm为机械转矩，通常取值为0；J为调相机转子转动惯量；D为摩擦系数；ωSC为转子角频率；ω0为系统角频率；δSC为调相机功角。

调相机通过在励磁系统中附加无功调节器来保证机组的无功出力和维持系统电压，控制框图如附录A 图A1 所示。根据图A1 可写出励磁系统的动态方程为:

调相机自身d、q轴电压电流与全局xy坐标相应分量满足坐标变换，即

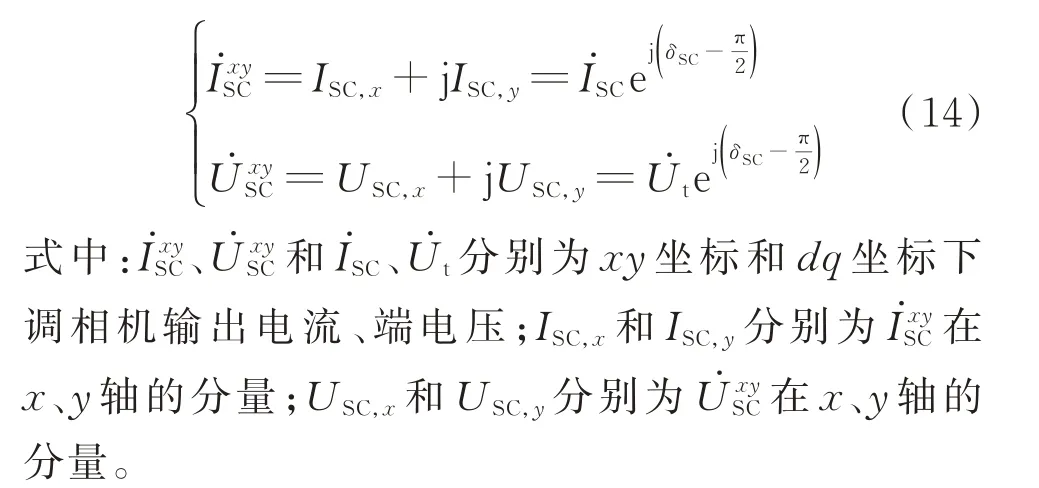
选择全局xy坐标下调相机的端电压作为输入、电流作为输出，将式（10）—式（14）在平衡点线性化并消去代数变量即可得到调相机的单机系统状态空间模型，如式（15）所示。

由式（15）可进一步得到调相机的频域导纳模型为:

式中:YSC(s)为频域导纳矩阵；I为单位矩阵。

1.3 闭环系统建模

由式（17）可得交流网络的动态方程为:

由式（18）消去交流网络内部的无源节点可得结构保持下的网络动态方程为:

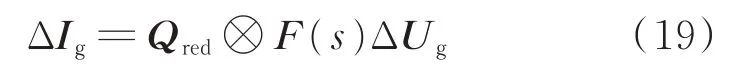
式中:Qred=QA-QBQ-1DQC。

联立式（9）和式（16），可得加装调相机后的新能源系统注入交流电网的电流为:

式 中:SSC=diag(SSC1，SSC2，…，SSCp)为 调 相 机 额 定容量组成的对角矩阵；SB=diag(SB1，SB2，…，SBn)为新能源设备的额定容量组成的对角矩阵。

为了方便说明配置调相机对多馈入系统小干扰稳定性的影响，这里假设各变流器以设备自身容量为基准的主电路参数标幺值相同，新能源出口母线电压间的相角差很小并可以忽略，故各新能源设备的导纳矩阵YPED(s)相同［4］。

至此，联立式（19）和式（20），得到系统的特征方程如式（21）所示。式（21）可反映多馈入系统中加装调相机后设备与交流网络的动态交互特性，下一章将基于式（21）说明加装调相机后系统的小干扰稳定性如何变化。

2 安装调相机后系统的稳定性分析

本章从电网强度的角度分析安装调相机对新能源基地小干扰稳定性的影响。在分析调相机接入对系统的稳定性影响之前，先简要介绍gSCR 的概念。

针对图2 所示的多馈入系统，当不考虑调相机接入时，系统的特征方程为:

图2 含调相机的多机系统Fig.2 Multi-converter system with synchronous condenser

式（22）等价为:

式（23）表明，在一定假设条件下，多馈入系统的小干扰动态特性可以由n个解耦的单馈入子系统表征，其中第m个子系统实际上是一台新能源设备经过线路（其线路导纳为λmF(s)）连接到无穷大电网的单机系统。一般来说，新能源并网系统的小干扰稳定性随着线路阻抗的增加而变差［4］。因此，多馈入系统的小干扰稳定性取决于最弱的单馈入系统（特征值λ1对应的单馈入系统），即系统稳定性可由式（24）决定。

文献［3］将拓展导纳矩阵S-1BQred的最小特征值λ1定义为系统的gSCR，gSCR 可以用来衡量多馈入新能源系统交流电网的强度并刻画系统的稳定裕度；gSCR 越大，意味着电网越强，系统越稳定；反之交流电网越弱，系统越容易产生不稳定问题。

下面利用gSCR 指标说明加装调相机对系统稳定性的影响。为简化说明，首先考虑调相机的安装数量为1 的情况，即p=1；后文分析结论表明，对于在系统中安装多台调相机的稳定性分析结果，可利用p=1 时的结论迭代得到。

由式（21）可得p=1 时，系统的特征方程为:

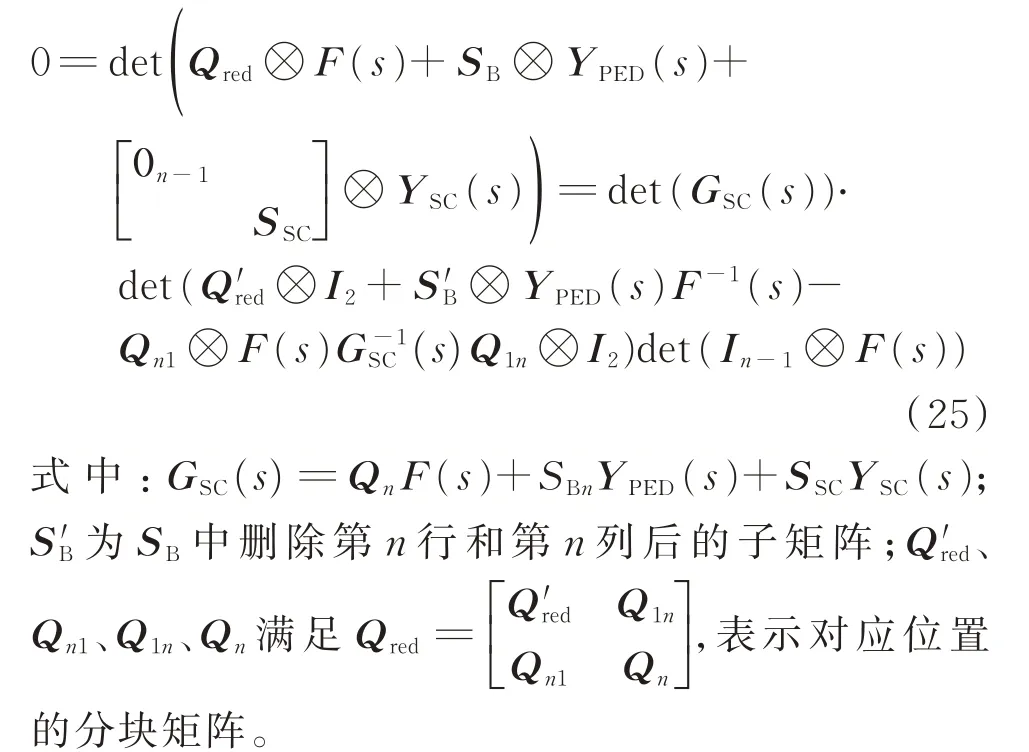
det(GSC(s))实际上表示的是在单机新能源设备出口母线加装调相机后接入无穷大电网系统的特征方程，该系统一般不会有不稳定问题，故det(GSC(s))不含有不稳定零点。且由于调相机具有维持母线电压的功能，其外特性通常表现出良好的电压源性质，其输出阻抗ZSC(s)(YSC(s)=Z-1SC(s)) 很小，则SSCYSC(s) 幅值通常远大于QnF(s)+SBnYPED(s)，因 此 有GSC(s) ≈SSCYSC(s)。从而分析式（25）的稳定性等价于分析如下系统。

式中:v和u分别为矩阵(S'B)-1Q′red最小特征值的左、右特征向量；o(·)表示求高阶无穷小量函数。

忽略高阶小量，则式（27）可进一步表示为:

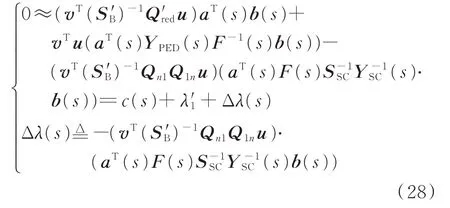
对比式（24）和式（28）并结合gSCR 的定义可以发现，加装调相机后可认为系统强度由λ1变成λ′1+Δλ(s)，通过比较λ′1+Δλ(s)和λ1的差值即可判断调相机接入后系统稳定性是提高还是降低。值得一提的是，一般在电力电子化电力系统宽频带振荡问题所关注的频段内（几十赫兹至几百赫兹），Δλ(s)的幅值通常远小于λ′1（后文算例将印证该性质），故可用λ′1来表征加装调相机后系统的强度。

λ1是矩阵S-1BQred的最小特征值，而λ′1实际上是删除矩阵S-1BQred中调相机接入节点对应的行列后（这里为第n行和第n列）矩阵(S'B)-1Q′red的最小特征值。根据矩阵交织定理［21］，有λ′1＞λ1恒成立，因此可认为加装调相机等效于提高了系统的gSCR，从而增强了系统的小干扰稳定性。安装调相机提高系统小干扰稳定性的机理从物理上可理解成:调相机本质是一种同步机，可以看作是具有很小的输出阻抗的电压源，新能源设备出口母线连接了调相机后，该母线电压得到很好控制，提升了系统的电压支撑强度，从而使得系统稳定性增强。

基于所得结论容易发现，对于在系统中安装多台调相机后系统的稳定性分析，通过迭代上述p=1的分析过程即可实现；系统的强度可以利用删除S-1BQred中调相机接入节点对应行列后的子矩阵的最小特征值来刻画。

3 调相机落点配置

第2 章分析说明了安装调相机等效于增大系统的gSCR，提高系统的小干扰稳定性，本章将研究如何合理配置调相机的落点，最大限度提升系统的小干扰稳定性。

考虑如图2 所示的多馈入新能源系统中安装p台调相机（p＜n）。根据第2 章结论，为使调相机接入后系统等效gSCR 提升最大，调相机的安装落点可以通过求解下面优化问题确定:

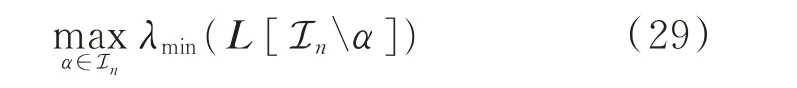
式中:L=S-1BQred；In= {1，2，…，n}表示新能源设备的出口母线节点集合；α∈In表示p个连接调相机的母线节点；L[ Inα]表示删除矩阵L中节点α对应行列后的子矩阵；λmin(·)表示矩阵的最小特征值。

式（29）是个组合优化问题，当接入的新能源数量非常多时，会存在组合爆炸的问题，不适合应用于大规模新能源接入的电力系统。研究经验表明，对于上述优化问题，通过迭代p次安装1 台调相机对应的优化问题所得的结果通常等于或接近最优解。后文算例将证实即使迭代所得结果并非全局最优解，也足以显著提高系统稳定性。具体来讲，每次删除L矩阵的1 行1 列，保证所得子矩阵的最小特征值最大化，迭代该过程p次即可得到调相机的最优落点。

值得一提的是，由于接入一台调相机实际上提升了相应新能源出口母线的电压支撑能力，基于物理认识可知，当调相机接在最薄弱的新能源出口母线处时，对系统的稳定性提升将会最大。因此，上述迭代优化问题的单步求解等价于确认当前系统最薄弱点，而多馈入系统的薄弱点对应于gSCR 参与因子最大的母线节点［4］，参与因子可由式（30）得到。这样一来就避免了每次迭代过程中多次求解矩阵特征值计算量大的问题。

式中:P1j表示第j个节点的参与因子；φ1，j和φj，1分别为当前拓展导纳矩阵L最小特征值的左、右特征向量的第j个元素。

综上，调相机落点配置的优化算法如图3 所示。需要说明的是，本章所提方法是从提高系统电网强度的角度（用gSCR 表征）来确定调相机在大型新能源基地中的位置，以最大程度提升系统的小干扰稳定性。实际调相机的选址问题还应考虑系统的大干扰稳定性、经济性等因素，这将是后续工作之一。

图3 调相机落点优化流程图Fig.3 Flow chart of optimal placing for synchronous condensers

4 仿真算例

本章将在MATLAB/Simulink 中建立详细的电磁暂态仿真模型，验证前文分析结论以及所提调相机落点配置方法的有效性，最大程度提升新能源基地的小干扰稳定性。

4.1 2 区4 机 系 统 算 例

考虑附录A 图A2 所示改进的2 区4 机系统。需要说明的是，本文的分析和结论对其他任意拓扑的新能源系统均是适用的。图A2 中，4 个新能源场站（每个场站用1 台变流器等值）通过1～4 号母线连接于交流系统，7 号母线通过线路电感连接于等值外电网，用于模拟多个场站接入弱同步电网。不失一般性，假设新能源容量均等于基准容量，设备控制参数、调相机与网络拓扑参数详见附录A 表A1。

附录A 图A2 所示2 区4 机系统中，新能源设备通过1～4 号母线接入交流电网，消去其他内部节点，可得结构保持下系统的扩展雅可比矩阵为:

同时可求得系统的gSCR 为2.70。为验证接入调相机等效于提高系统的gSCR，首先需验证式（28）中Δλ(s)的幅值足够小，Δλ(s)的波特图如附录A 图A3 所示。从图中可以看出，在新能源振荡问题通常关注的频段（10～1 000 Hz）内，Δλ(s)的幅值相比于λ′1可以忽略，故Δλ(s)对式（28）中主导极点的影响可以忽略不计，调相机接入后的系统电网强度可以由λ′1来衡量。

考虑在2 区4 机系统中接入2 台调相机，下面利用前2 章分析结论确认能最大程度提升系统小干扰稳定性的调相机落点方案。按照图3 所示的算法，特征值λ(1)1对应的节点参与因子如附录A 表A2 所示，由表A2 可知节点4 的参与因子最大，第1 台调相机安装接入节点4 对系统稳定性提升效果最好。

根据第1 步迭代结果，删 除L（1）中第4 行和第4列得到L（2）及对应的节点参与因子为:

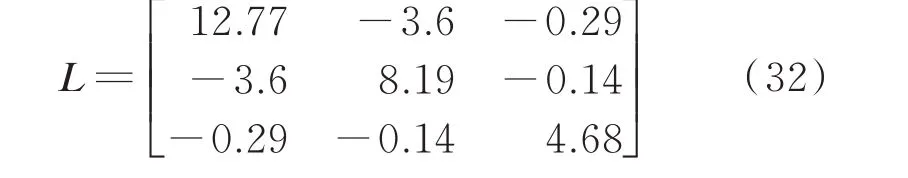
由附录A 表A3 可以看出，第2 台调相机的最优落点为节点3。故2 台调相机分别安装在节点3 和节点4 可以最大程度地提升系统的稳定性。

根据前文分析，从提高系统小干扰稳定性的角度考虑，调相机的最优落点可以通过求解式（29）的组合优化问题得到。附录A 表A4 给出了对式（29）枚举求解的结果，可以看出调相机接在节点3 和4后，系统的gSCR 最大，与利用图3 所示的迭代求解方法得到的结果一致，验证了所提调相机落点配置算法的有效性。

图4 给出了调相机安装在不同位置时系统的特征值，当没有安装调相机时（情况1），由于新能源设备和交流电网的交互作用，系统处于临界稳定状态；当在节点1 和节点2 分别加装调相机后（情况2），系统主导特征值M1向左半平面移动，说明调相机的接入提高了系统的阻尼；当在节点3 和节点4 分别加装调相机后（情况3），系统的阻尼显著提升，与上述调相机的最优落点结论相吻合。需要说明的是，调相机接入后，系统中增加了一组新的振荡模式（对应系统主导特征值为M2），这实际上是调相机的转子振荡模式，通常通过调相机的励磁控制能使该模式具有足够阻尼，不会引起振荡。

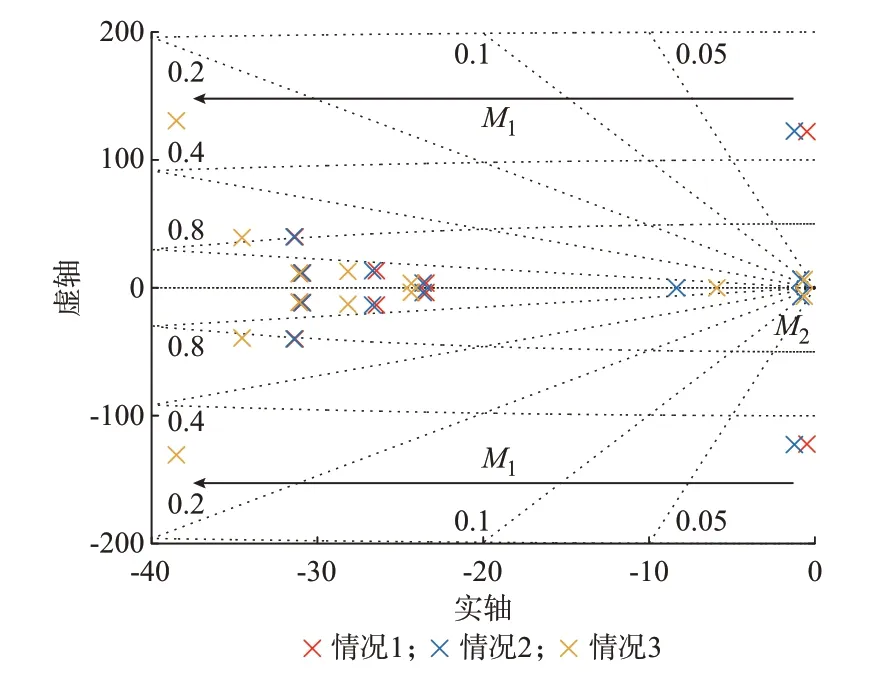
图4 系统的主导特征值Fig.4 Dominant eigenvalues of system

附录A 图A4 给出了调相机安装前后以及调相机在不同落点时4 台变流器输出功率的时域波形，在t=0.5 s 时，负荷3 发生扰动并在0.02 s 后切除扰动。由图A4 可知，在未安装调相机之前（情况1），变流器输出的有功功率等幅振荡，系统处于临界稳定状态；当调相机接入节点1 和节点2 后（情况2），系统阻尼比提高，振荡波形开始收敛，说明调相机接入后提高了系统稳定性；而当调相机接入节点3 和节点4 后（情况3），系统具有很高的阻尼比，扰动后的波形能快速收敛，大幅提升了系统的稳定裕度，验证了本文所提调相机落点配置方案的有效性。

4.2 9 机39 节点系统算例

为了进一步验证所提调相机配置方法在大型新能源基地中的有效性，考虑一个包含9 个新能源场站（每个场站用1 台变流器等值）的多机系统，如附录A 图A5 所示。该多机系统的网络拓扑实际上与新英格兰IEEE 39 节点系统是一致的，交流网络参数见附录A 表A5，调相机和变流器的基本控制参数与附录A 表A1 一致，其中，PLL 比例和积分参数分别修改为155 和1 800 以提供临界稳定情况。

附录A 图A5 所示系统的广义短路比λ1=3.31。利用第3 章中提出的方法在39 节点系统中安装2 台调相机以提升系统的小干扰稳定性。首先，直接利用枚举方法求解式（29）中的优化问题，得到调相机落点的全局最优解的位置为(1，4)，此时系统的gSCR 变为λmin(L[ Inα]) =14.43。可见，在节点1和4 处安装调相机，系统的电网强度显著增加，小干扰稳定性提高。另外，为了避免枚举求解式（29）计算量大的问题，采用图3 的迭代求解算法，得到调相机 的 安 装 位 置 为（9，8），此 时 系 统 的gSCR 为λmin(L[ Inα])=12.03。可以看出，虽然迭代求解算法得到的是一个次优解，但系统的电网强度仍然显著提高，证明了本文所提方法的有效性。如何高效地求解式（29）将是后续研究的工作之一。

图5 给出了调相机安装在不同位置时，9 台变流器的时域有功功率（PE1，PE2，…，PE9）响应波形（其中0.2 s 时系统遭受扰动并在0.02 s 后清除）。

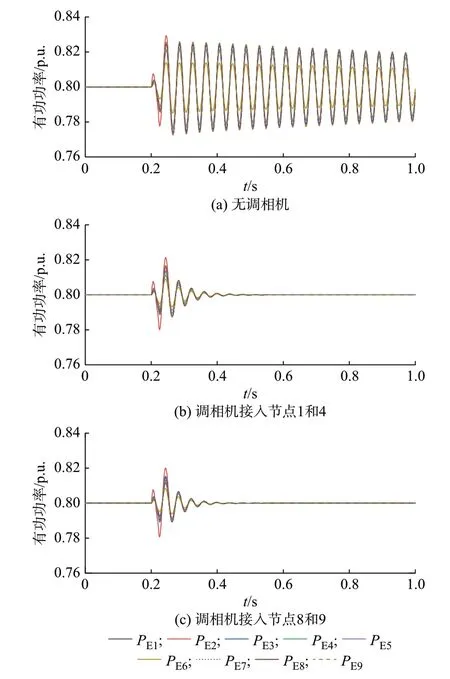
图5 9 机39 节点系统时域波形Fig.5 Time-domain waveforms of 9-machine 39-bus system

图5（a）中，在没有安装调相机的情况下，扰动后变流器的输出功率持续振荡，系统的阻尼比非常低，小干扰稳定性差。相比之下，当调相机接入节点1 和节点4 时，系统具有较高的阻尼比，如图5（b）所示。根据迭代算法结果，将调相机接入节点8 和节点9 后，系统在遭受小扰动后变流器输出功率也能迅速收敛，可见此时系统也具有良好的阻尼性能。上述仿真再次验证前文的分析结论，表明配置调相机可有效提高大型新能源基地的小干扰稳定性。

5 结语

本文研究了在大型新能源基地中安装调相机对系统小干扰稳定性的影响。通过建立含调相机的多馈入系统的动态模型以及严格数学推导，说明了在系统中加装调相机等效于增大系统的gSCR，从而提高了系统的小干扰稳定性。在此基础上，将提高系统小干扰稳定性的调相机选址问题转化为增加电网强度（即增大gSCR）的问题，仅通过求解与网络参数和变流器容量有关的优化问题来确定调相机的最佳位置，可为含大规模新能源电力系统的运行规划提供指导。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。