唤醒经验 提升核心运算能力——小升初专题《数与运算》教学反思

朱湘莲

（昆山市陆家镇菉溪小学，江苏昆山 215300）

在小学数学教学中，《数与运算》是小学数学最基础的知识，贯穿于各个年级，内容繁多，是学习初中数学的基础。《义务教育数学课程标准（2011年版）》也将“运算能力”作为十大核心概念之一。如何在学生已有六年学习经验的基础上，进一步理清数的意义、数的运算，同时在运算的过程中更加合理地运算、简洁地运算，结合自己的教学实际作如下反思：

一、分类整理，让概念更加直观

数的认识知识点多且较为零散，整个小学阶段涉及整数、小数、分数（百分数）的意义、计数方法、表示方式和分类等，帮助学生弄清相关知识的来龙去脉、找到知识间的联系、形成知识的网络尤为重要。在复习整理的过程中，教师可以借助数轴，构建数系网格，帮助学生理清数的意义；通过分类整理，进一步明确数与数之间的关系。

（一）借助数轴，理清数的意义

数轴应用贯穿于“数的认识”的学习。数的概念比较抽象，而数轴具有直观和抽象的优势，能充分体现数的本质属性，借助数轴，以问题引导学生在解决问题的过程中调动已有的知识和经验，利用几何直观理清各种数的意义、计数方法和数的分类，同时，通过相互转化，进一步加深理解数与数之间的联系和区别。教师可以借助数轴，帮助学生理清数的意义，如下：

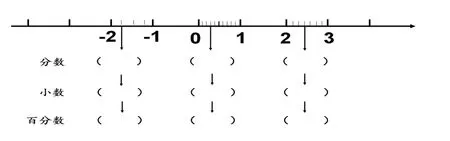
（1）大于0的数是（ ），小于0的数是（ ），0（ ）。0、1、2、3、-1、-2……这样的数叫（ ），1、2、3……是（ ），-1、-2、-3……是（ ）；0、1、2、3……这样的数又叫（ ）。

（2）请你找到0.4这个点，这个点还能表示（ ）、（ ）、（ ）……（填小数），这个点如果用分数表示，可以表示（ ），（ ），（ ）……

（3）在括号里填上合适的数。

（4）上面数轴上的3个分数中的“3”分别表示( )、（ ）、（ ）。“3”还可以表示（ ），比如（ ）；还能表示（ ），比如（ ）。

通过第（1）小题的练习，帮助学生进一步理解正、负数的概念，知道数可以分成：正数、0、负数，0和整数也叫自然数，借助数轴，能使抽象的概念变具体：以0为分界点，比0大的数是正数；比0小的数是负数。正数包含正整数、正分数、正小数；负数亦是如此。

数轴是学生学习“数的认识”最直观的几何模型，是数形结合的具体体现，是培养学生数感的有效载体。小学数学教学中，借助数轴，学生能清晰地看到“数”与“数”之间的联系，为数学知识学习奠定坚实基础。

（二）分类整理，明晰数的分类

在低、中段的学习中，数的认识重点放在数的意义和计数方法上，五年级下册开始学习“因数和倍数”，其内容抽象程度高，是“数的认识”的难点之一，因数和倍数是两个既相互对立又密切联系的概念。整理时，注意知识的内在联系，把相关的知识内容组织成“块”，一块一块地进行复习，借助分类练习，把抽象的概念以直观的方式表示出来，帮助学生进一步明确数可以按不同的标准进行分类。

在练习的过程中，学生加深了对奇数、偶数、质数和合数概念的认识，知道按不同的分类标准，可以把整数分成不同的类别。按是否是2的倍数，整数可以分成奇数和偶数；根据一个数因数的个数，整数还可以分成1、质数和合数。然后引导学生进一步思考：上面的数还可以怎么分类，通过观察数的特征，学生很容易发现：还可以按是否是3的倍数、是否是5的倍数进行分类，在分类的过程中，既巩固了2、3、5的倍数的特征，又促进了学生对概念的深入辨析。

二、重点训练，夯实计算基础

“数的运算”是小学数学重要的核心内容，包括整数、小数、分数的四则运算意义和计算法则、运算定律和简便运算以及四则混合运算三部分。《义务教育数学课程标准（2011版）》强调：培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。学生学会在计算过程中根据运算符号和数的特征以及数与数之间的联系，合理灵活地选择计算方法。在复习过程中，帮助学生理解数的运算的本质，有助于从数学的原理认识数的运算，进而科学合理地进行数的运算。

（一）沟通联系，理清计算本质

在练习过程中，要帮助学生进一步掌握整数、小数、分数的四则运算方法，理清四则运算的算理。数的运算首先是从整数开始，在掌握整数加、减、乘、除运算的基础上，再学习小数和分数的运算。小数和整数都是十进制的，所以在运算过程中可以顺利地将整数四则运算的方法迁移到小学四则运算，而分数要比小数复杂一些，因为分数的表现形式不是十进制，需要先通分统一分数单位，从分数单位的角度理解分数加减法意义。

比如：在复习时，可以通过设计以下练习，帮助学生巩固整数、小数、分数加减法的运算法则，并在练习的过程中，进一步比较整数、小数、分数加减法相同点和不同点。

整数加减法、小数加减法计算时都是相同数位相加减，整数加减法表现为相同数位对齐，小数分数加减法表现为小数点对齐。而分数加减法先要把异分母分数转化成同分母分数，分母不变，分子相加减。通过比较与沟通，发现整数、小数、分数加减法的本质是相同的：都是相同计数单位的数相加减。这样，学生就从整体上、本质上理解和掌握了加减法的计算法则。在寻求数的运算本质的时候，梳理这些运算的共同特征非常重要。

（二）题组训练，提高计算技能

整个小学阶段知识繁多，不同的数学知识有着不同的内涵，其涉及的数学问题也是多种多样的，但是，不同的问题之间也有着千丝万缕的联系，如何使学生能够更有效地进行相关知识的联想和学习，教师要善于对学生进行系统的题组训练，将前后有联系的知识放在一起训练，让学生在练习中区分联系，找到知识间的衔接点。

如在整理整数、小数、分数乘除法时，可以设计以下题组，在比较中巩固计算法则。

对于小数乘法、除数是小数的除法、分数除法的计算法则的归纳整理，运用题组训练的方式，让学生在对比中明确：小数乘法可以转化成整数乘法、除数是小数的除法可以转化成除数是整数的除法、分数除法可以转化成分数乘法，帮助学生进一步感受“转化”的思想，将转化的思想内化为自己的思维方式。以上环节利用数学题组训练，引导学生进行思考、练习、小结，使学生全面梳理所学知识。

三、拓展延伸，关注知识衔接

学生数学思维的整合性表现为能对所学知识进行分析、综合、归类及重新组织，使其系统化、条理化。数学的逻辑性很强，概念之间相互依赖、相互转化，组成一定结构。同时，各个知识之间又存在着客观的逻辑关系，形成各知识间的结构，这些知识结构必须在数学教学过程中得以完善和运用。“数与运算”这部分内容的中小学衔接，教师要引导学生回忆所学知识，并加以归纳整理，使之系统化，纳入学生的认知结构，为初中学习打下基础。拓展延伸的方式是多维的，可以在知识的广度和深度上挖掘，也可以在学习方法、数学思想上进行延伸。

（一）感悟技能方法——加强学生数学运算能力

数的运算涉及许多知识，主要有四则运算的意义、方法、混合运算的顺序、运算律以及简便计算等。在整理系统知识时，要帮助学生整合运算经验，提升运算技能，形成运算能力。

如计算1.25×88，要用一题多解的思想帮助学生提升运算技能。同一道算式，我们找到了不同的计算方法，通过整合学生的运算经验，提升学生的运算技能，发展数学核心素养。

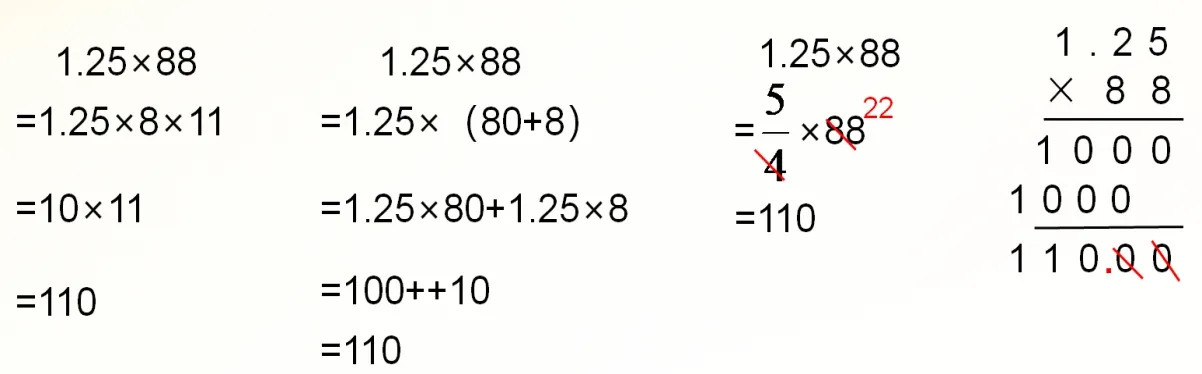
计算1.25×88有4种方法，方法一：把88分成8×11，再利用乘法结合律，先算1.25×8=10，再算10×11=110。

方法二：把88分成80+8，利用乘法分配律，1.25分别乘80和8，再把它们的积相加。

方法三：把1.25转化成分数进行计算，用分母4和整数88进行约分，也能很方便地算出得数。

方法四：还可以用列竖式的方法来计算。通过观察比较，发现列竖式的方法和运用乘法分配律简算，过程是相似的。分别计算了1.25乘80和1.25乘8。这样的观察对比，可以使学生对已经熟悉的知识有一种新的认识，对简便运算产生更深刻的体会，同时也感受到数学知识的互通性。

小学数学是一门涉及知识极为广泛的学科，其中包含着各种各样的定义、概念和公式，其对学生能力的考察也是非常严格的。在进行教学的过程中，教师不仅要重视数学知识的传授与讲解，更要高度重视对学生解题能力的训练，使小学生能够在学会知识的同时具备良好的信息提取和问题解答能力。在各种各样的数学问题中，一题多解的情况是非常常见的，但是，部分小学生在学习的过程中不喜欢进行深入的理解和探究，这就导致他们无法有效地进行多种解题思路的发掘，为了高效地解决这样的教学问题，使小学生能够真正在学习的过程中有所收获，教师要善于对小学生进行训练，引导他们从不同的角度对解题方法进行思考。

（二）渗透数学思想——培养学生数学思维能力

运算能力的培养与发展不仅包括运算技能的逐步提高，还应包括思维素质的提升和发展，真正把运算能力作为数学核心素养，就要从纯粹计算的外表进入到学生思维的核心。向学生渗透一些基本的数学思想方法，是数学教学改革的新视角。让学生掌握基本数学思想方法，既能使数学更易于理解，又能让学生易于记忆。在小学数学教学中，经常用到的思想方法有：抽象、推理、模型、数形结合、化归、符号化数学思想等。在教学中，老师要有意识地渗透这些基本的思想方法，学会用数学方法思考和解决问题，对数学学科的后续学习有着广泛的运用。

又如：“转化”的思想在小学数学学习中具有广泛的应用，不但图形的教学可以用到转化，代数中的很多知识也可以用到转化。在笔算小数乘法、小数除法和分数除法的过程中，学生同样体会到了数学的转化思想。

在中小学的学习过程中，数与运算都是非常重要的教学内容，也是培养学生核心素养的关键所在，在练习过程中，我们不仅要帮助学生巩固知识和技能，还要使学生在数学思想方法、思维方式和学习方式上逐步与初中接轨，为初中学习打好基础。