运用数学模型验证地球上两点间最短路径问题

2022-02-28宋音

科学咨询 2022年2期

宋音

（诸暨市第二高级中学，浙江诸暨 311800）

数学方法是验证规律运动的可行方法。因此，现如今很多地理问题的描述方式，是采用以数学公式为基础的数学建模形式。本文讨论的地球表面两点间最短路径问题，也是一种规律运动。学生在学习课本知识时对书本中“最短路径是球面上经过两点的大圆劣弧段长”结论存在疑惑，但是学生没有方法验证这个结论是否正确。本文将尝试用数学公式，采用Matlab工具进行数学建模，验证地球表面两点间最短路径是否是过球心的大圆劣弧线段，给学生寻找更加直观简单的学习最短路径方法。

一、材料准备

（一）光滑地球模型

假设地球表面为光滑曲面，没有地形起伏和海陆差异，O为该球的球心。

（二）数学建模工具

本文采用数学建模工具Matlab R2016a软件，以编程形式，实现数学公式模型，验证本文猜想。Matlab软件是广泛运用于数学建模、仿真和涉及的数学软件。因此本文利用Matlab软件来判断该结论的可行性和实用性。

二、模型理论验证

在光滑曲面上任取两点作为起终点，其中A为起点，B为终点，AB之间的曲线路径是经过AB两点的圆上曲线。本文假设有三个不同圆心的圆，具有三条不同路径，路径长度也不一样，效果图如图1。通过观察图1，本文可以利用球的对称性，用来建立统一的坐标系来比较三条路径长度。

在构建统一的坐标系之前，本文先考虑如何计算AB点之间曲线长度问题。根据图3以及圆的相关数学知识，可以了解AB两点之间的劣弧长度就是扇形ABO的弧线长度，该长度根据扇形的弧线计算公式(1)可得。

式中θ指扇形弧线所对角的弧度值，r为扇形所在圆的半径。

观察图1和图2，本文发现点A与点B是关于线DCO对称的，将点A与点B用投影在面OCD上，这样就可以将扇形ABO的半径和弧度的问题在面DCO中解决，如图3所示。根据扇形的知识可知，扇形角度θ可以采用直角三角形反余弦函数求解，求解公式如式子(2)。因此，本文只需要线段OC和半径OD的值，就能求解弧线ADB的值大小。

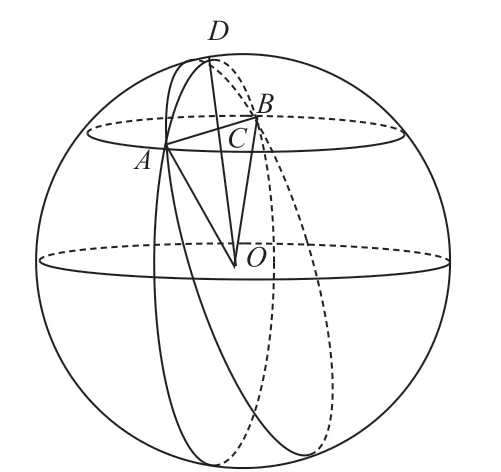
图1 三个不同圆心的曲线路径

图2 AB之间弧线的示意图

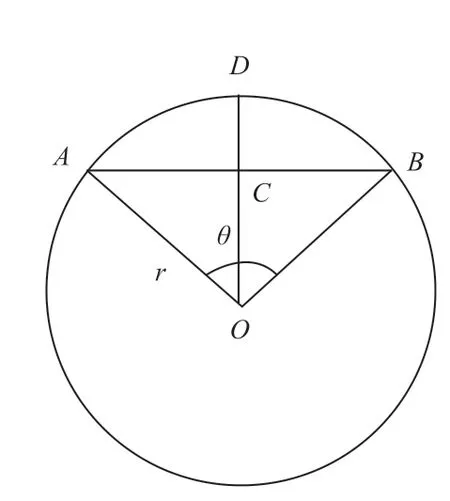
图3 对称剖面平面DCO

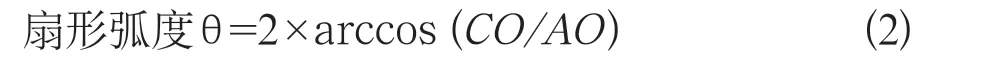
式中AO的值为扇形所在圆的半径，CO为直角三角形直角边的长度。

通过面DCO剖分球体后，得到如图4所示的结果。其他不同的圆在面DCO的投影都是一条直线。从图4可以看出，只要找到不同直线的圆心所在位置，利用点C的位置，就可以求解不同圆心O与点C之间的线段距离。同时找到经过点C的直线与以DO为半径的圆所相交的两点之间直线长度，即不同圆的直径，可得出不同圆的半径值。点的位置，采用坐标系的形式表示。本文采用直角坐标系构建坐标位置。综上所述，求解点A与B的最短路径问题，转换为求解经过点C的不同斜率直线与固定大小的圆所截取线段的问题。

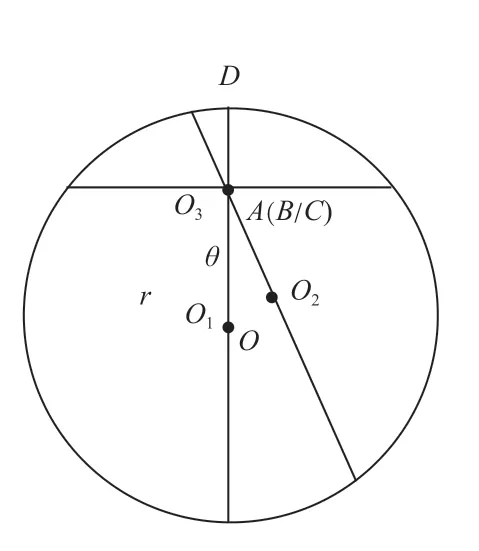
图4 平面DCO中ABC点位置

三、模型构建

本文在直角坐标系中，构建经过定点A的不同斜率直线与固定圆所截取的线段，该线段的中点为圆心，线段长度为圆直径，点AB在以该圆心和半径所构成的圆上扇形弧线长度就是该圆上AB点之间的弧线路径长度。通过比较不同弧线长度大小，选出最短的弧线所在圆的圆心是否是球心来验证本文猜想。

（一）固定圆的建立

在直角坐标系中，建立圆心在（25，25），半径为10单位长度的圆。以此数据建立的圆基本方程，后续过程中本文求解直线与圆的交点问题，就可以避免数据出现负数情况，影响计算结果。

（二）随机点的确立

本文采用Matlab软件中的随机函数，随机抽取100个随机样点的x坐标。因为随机点坐标（x，y）在固定圆内，所以满足圆数学方程。因此基于此编写相关数学模型选取随机点。

（三）不同直线的确立

随机点的选取确定后，因为存在固定点，本文可以根据直线的点斜式方程建立直线方程，点斜式方程见式子(3)。但是点斜式直线方程存在一个缺点，不存在经过固定点并且垂直于X轴的直线，因此需要补充一个垂直X轴的直线与固定圆的弧线情况。因为Matlab软件中对于数学计算都是采用确定值计算，所以该斜率范围0-2π内平均选取200个相同间隔的数值，代入数学模型中计算。

式中k为斜率，（x0，y0）为固定点。

（四）模型思路

第一，选取一个随机点及一个斜率，构建点斜式方程，与圆的基本方程联立，求解直线与圆的两个交点坐标。第二，本文采用中点坐标公式，结合两个交点坐标求解中点坐标，该坐标即扇形所在圆的圆心坐标。该圆的半径由两个交点的线段长度公式求解所得。第三，根据随机点坐标与圆心坐标，求解这两点间距离CO。再根据距离CO和半径求解扇形弧线所对角的弧度。本文利用弧度和半径求解扇形的弧线长度，即点A与B在这个圆的路径长度。第四，依次重复上诉三个步骤，将剩余的斜率和随机点组成的直线方程都计算完成，形成200个路径长度。本文寻找出这200个长度值中最小值，该最小值所在的圆心即最短路径所在圆的圆心。再运用相对误差的方法验证该圆心坐标与固定圆圆心坐标（25，25）的距离误差大小。第五，本文再选取99个随机点，重复上述四个步骤，测试总共100个随机点的最短路径所在圆的圆心坐标与固定圆的误差。

四、模型结果

从结果图5可知，某一随机点的不同路径长度变化是有一定规律的，和斜率的变化有一致性。不同点的最短路径所在圆的圆心坐标展示在图5(3)，可以看出，100个随机点的最短路径所在圆的圆心和固定圆的圆心距离相差不大，并从图5(4)相对误差分布图中看出，大部分圆心与固定圆心的相对误差是在0.01范围内，本次模拟中大部分随机点的圆心坐标相对误差甚至小于0.005。这个结果表明任意随机点的最短路径所在圆心都是在固定圆的圆心。而固定圆的圆心就是假设前提下地球的球心。因此本文可以验证，地球上任意两点间的最短路径就是该两点与球心所构成的大圆上劣弧。

图5 组合结果图(1)不同斜率下路径长度；(2)斜率范围图；(3)不同随机点最短路径所在圆心分布图；(4)不同随机点最短路径所在圆心与固定圆圆心相对距离误差分布图

五、课堂设计

根据前面验证工作，本文可以确认地球上任意两点间的最短路径是经过两点大圆上的劣弧长。课堂设计的思路可以参考球上大圆的数学性质和验证过程中采用的数学思想。

（一）最短路径问题的提出

在现实生活中，人们喜欢省时省力的活动，选取交通线路时也是参照这一原则。尤其是飞机航线等路径，这些路径不用考虑地形等其他影响路径因素，只需要考虑路径长度问题。所以飞机路径是常见的最短路径的运用场合。

（二）证明最短路径的存在形式

那么怎样的路线才是最短的路线呢？借用上文中的图1与图3，给学生讲解经过两点间的线在球面上绘制一圈后都会形成圆形，而这个圆形路线上，最短距离肯定是选取圆上的劣弧段。而不同圆的劣弧段是不同的，所以要计算不同的圆上劣弧段长度再进行长度的比较，选取最短长度。教师可以直接将模型结论展示给学生，通过这个数学模型证据，让学生明白这个结论是准确的。

（三）最短路径的绘制

学生如何绘制两点间的大圆是球上两点间最短路径问题应用上必不可少的能力。绘制大圆，就得明白大圆在球上的数学规律。首先是大圆的圆心一定在球心上，或者是圆心的投影点在侧视图中两个大圆的交点上；然后大圆的绘制是利用圆内三角形的性质来绘制，也就是用线段连接圆心和球上两点，形成三角形，再利用圆心和半径绘制大圆。

绘制大圆一般分为三种情况：一是两点在一个已知大圆上；二是两点在同一个南/北半球；三是两点在不同南/北半球。

第一种情况，直接采用已知大圆来寻找最短路径就行。已知大圆如赤道、经线圈和晨昏线等。第二种情况，绘制的最短路径如图6所示，绘制方法如下：连接球内点A与点B的连线，根据扇形中垂线原理，可知点C为三角形OAB中AB边上的中点，OD线段为AB边的中线延长线。根据点D为一个经线圈上点，该经线圈使得点A点B的经线对称，并且点D也在OD线段上，可得点ABD在球面的一个圆上，且该圆是以点O为圆心的大圆。第三种情况，绘制最短路径就是连接不同半球的两点形成的圆即是大圆，其劣弧就是最短路径。原因是不同南北半球的点连线肯定要经过赤道，球心就是赤道的圆心，该连线形成的圆面肯定会经过球心，所以该圆肯定是大圆。

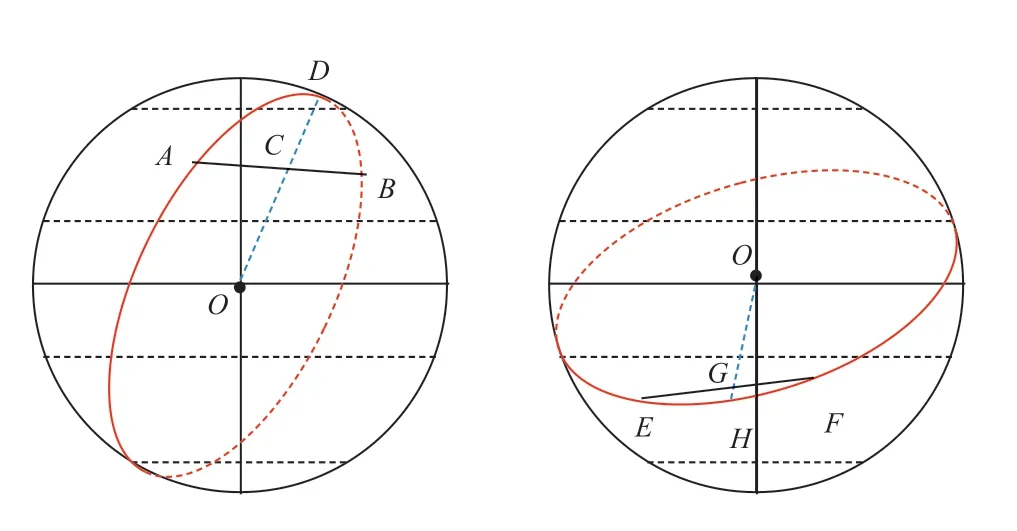
图6 相同南/北半球两点间最短路径

（四）最短路径的应用

新课标中关于最短路径的考查内容主要集中在最短路径的判断、行进方向的判断。其中最短路径的判断和上文中路径的绘制是相似的，包括路径的位置，弯曲凹凸方向等等。学生能够理解路径凹凸方向和球心是相反方向，球心在赤道上，所以路径的凹凸方向都是路径凸向高纬度地区的形状。另一个行进方向的问题，由于最短路径都是曲线，行进方向是有变化的，所以最短路径的行进方向判断要分段判读。在经纬网地图上判读行进方向，只需要将最短路径投影到经纬网上，然后根据投影后的行进方向在经纬网上的变化来判读。在普通地图或者是含有指北针的地图上判断，需要以指北针或者“上北下南，左西右东”口诀为参照，进行行进路线的投影，然后根据投影后的行进方向变化来判读。