软土基坑开挖对等效水平抗力系数的影响

贾 凯，王翠英

(湖北工业大学土木建筑与环境学院，湖北 武汉 430068)

随着城市建设的迅猛发展，在市区各类建筑、地下管线、城市干道等已有工程设施密集区域进行深大基坑施工越来越普遍，这对现代深基坑的设计与施工提出了更高的要求。而现行基坑设计模式是静态的，过于简化，难以真实反映实际情况。考虑时空效应的三维动态设计理论，软土基坑基于时空效应的新的围护结构设计方法[1]被提出,该法旨在准确反映工程实际、且计算参数少，易为工程设计人员接受。即在基坑主动区仍采用常规设计方法将土压力作为施加在围护结构上的水平荷载，而在被动区则使用等效水平抗力系数Kh这个唯一的计算参数，来模拟开挖过程中在各种施工因素影响下工程土体的综合性状。许多学者对此进行了研究，徐中华等[2]结合实测数据对水平抗力比例系数进行了反演分析，确定了其合理取值范围。刘亚文等[3]运用等效水平抗力系数Kh设计方法, 并结合基坑监测数据, 指出考虑时空效应对基坑施工的影响具有重要意义。刘成禹等[4]通过建立有限差分方程，提出了一种基于土体水平抗力与围护结构侧向水平位移的关系曲线。刘国彬等[5]根据现场实测资料的整理与程序反分析，认为Kh是考虑时空效应等因素影响下，能反映基坑开挖变形的综合参数。本文以武汉君临天下A地块基坑为依托，建立了分层开挖与支护的三维有限元模型，通过挡墙位移监测值与有限元模型计算值求出了Kh值，以此来研究基坑的不对称几何形状、不对称荷载和被动区加固对Kh变化规律的影响，研究成果可为类似工程的设计与施工提供参考。

1 被动区等效水平抗力系数分析

1.1 被动区等效土体水平抗力系数Kh

等效土体水平抗力系数是对弹性杆系有限元法中的弹性抗力系数这一概念的改用。因传统杆系有限元模型未充分考虑土体的流变性和应力分布情况对围护结构受力变形特性的影响，给设计造成了安全隐患。然而大量工程实测发现土压力和弹性抗力系数不仅与土体物理力学指标有关，还与基坑的开挖方式、顺序、时间、空间和坑周荷载分布密切相关，即会随工况的变化而重新分布[6]。而等效土体水平抗力系数Kh正是考虑了以上各类因素对土体工程性状的影响，即Kh值可视为上述众多影响因素的函数。

由于基坑的内支撑和围护结构二者组成了空间框架体系，因此该体系的内力与变形情况需按空间框架模型来计算[7]。在该模型中为使围护结构、周边土体和内支撑体系节点三者的位移与实际工程最大程度相符。可将围护结构转换为等刚度的板单元，并在被动区土体单元节点位置设置非线性弹簧单元来模拟。此时的被动区水平抗力系数Kh已不同于传统意义的弹簧弹性系数，而是对应于一定工况下能综合反映土性和随时空效应等复杂因素变化而变化的参数。地基被动抗力分布如图1所示。

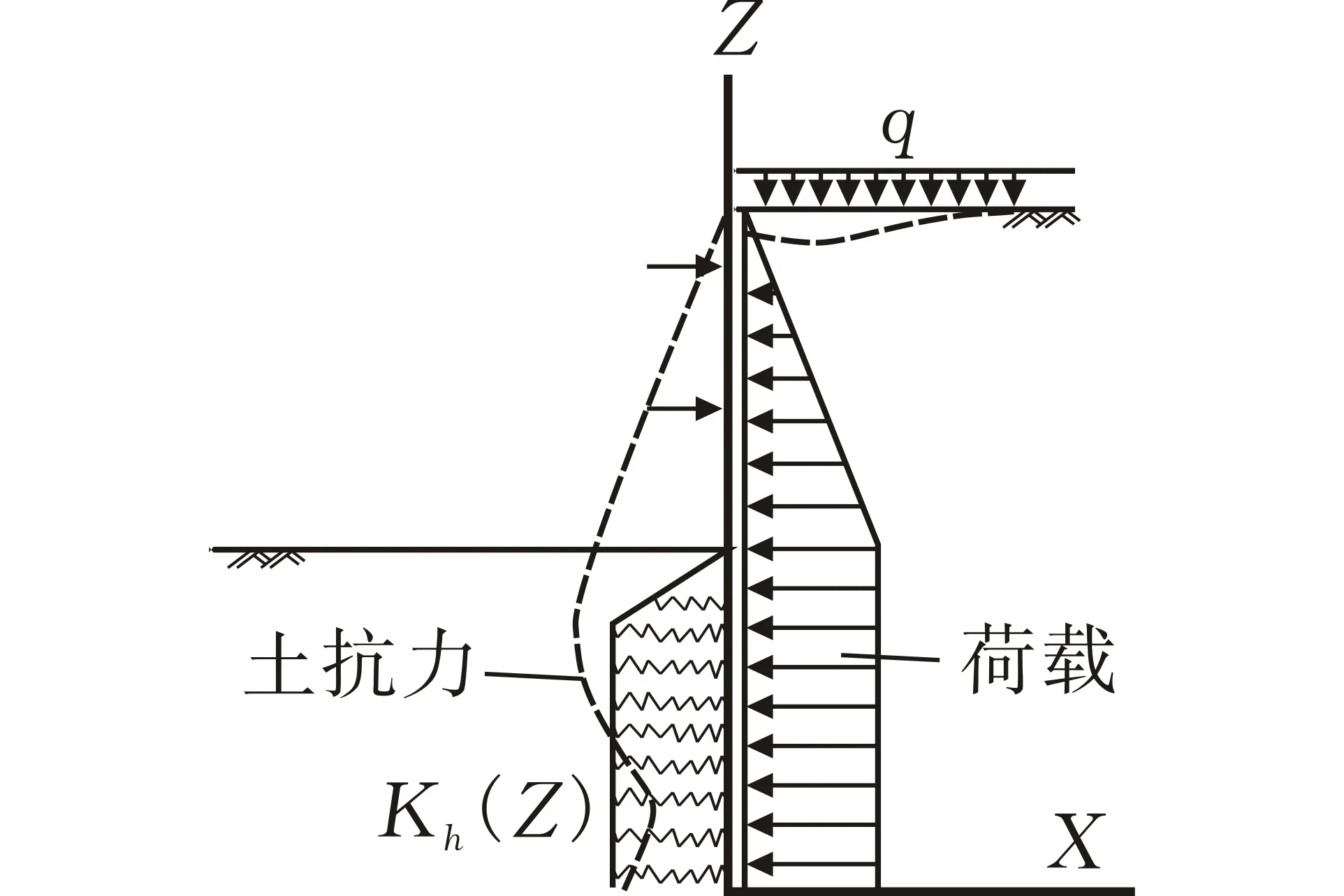
图 1 围护结构计算简图

1.2 Kh的计算思路

常规土压力计算中，采用经典朗肯或库仑土压力理论。事实上，基坑围护结构的变形量有严格的控制要求，被动区土体并未达到被动极限平衡状态而是处于弹性阶段，即土压力由静止土压力逐渐向被动土压力状态过渡，可称为被动抗力。由静力平衡条件有：

Kh=P/δ

其中：p为被动区土体的被动抗力；Kh为被动区土体等效水平抗力系数；δ为围护结构水平位移。

以基坑监测数据为依据，建立了三维有限元模型，使数值模拟所得的围护结构水平位移计算值与实测值逼近，即认为当前Kh值为该工况下被动区土体的等效水平抗力系数。该系数实质是被动区土体产生单位位移所需要的力，等价于被动区土体抵抗变形的能力。

2 不规则基坑不对称荷载被动区加固对挡墙位移的影响

2.1 基坑几何形状的影响

几何形状不对称的基坑存在着显著的坑角效应，且坑角效应对基坑长边与短边处的土体变形影响程度各不相同[8]，当基坑边长较小时，基坑边长中部的土体位移未达到或者正好达到平面应变状态下的土体位移;而当基坑边长较大时，坑角效应仅对距坑角一定范围内的土体位移产生影响，此范围之外，土体的变形可近似考虑为平面应变状态。基坑长边或短边外侧土体位移如图2。

(a)围护墙短边

围护结构的变形与到基坑角部相对距离的大小有关，当与基坑角部相对距离较小时，因相邻墙体之间、土体与墙体之间相互作用复杂，致使坑角效应明显，变形往往较小，而随着与角部相对距离的增大，坑角效应逐渐减弱，围护结构变形逐渐增大。当基坑边长较小时，围护结构最大位移发生在坑边中部，而当基坑边长较大时，在距离角部一定范围，其变形量已达到最大值并逐渐趋于稳定，可认为不再受坑角效应影响。

2.2 不对称荷载的影响

作用于基坑周边的各类荷载，均会影响土体的应力历史和应力路径，进而影响作用于围护结构上的侧压力[9]。当基坑开挖卸荷时，围护结构内外两侧将产生不平衡土压力，同时坑周的不对称荷载还将加剧两侧土压力的不平衡性，导致围护结构的非对称受力与变形。又因软土具有流变性[10]，作用在围护结构上的土压力将随时间不断变化，荷载较大侧土体相较于荷载较小侧土体处于较高应力状态，由此加大了相应侧土体的流变速率，故随着工况的进行，将对等效水平抗力系数Kh的衰减速率产生较大影响。

2.3 被动区加固的影响

软土基坑在不均匀荷载作用下，围护结构易产生非对称变形,形成由坑底绕过围护结构底部延伸至坑外地表的位移场，最终导致基坑发生失稳破坏。被动区加固是基坑工程中常用的土体加固改良方法,加固后形成的复合土体强度指标相比未加固前的土体有所提高[11]，其增加的量值与加固体范围有关。以往设计人员在确定加固范围时往往具有很强的主观性，因被动区加固后对其等效水平抗力系数Kh有相应影响，若知道加固后的Kh值则能大大增强对施工过程中基坑变形和稳定性的控制。

3 工程实例及有限元模型

3.1 工程概况与周边环境

武汉君临天下A地块项目，基坑最大长度210 m，最大宽度106 m，平均开挖深度12.1 m，其形状为不规则多边形。周边环境极其复杂，北侧为7-8层居民楼，西北侧为3～32层居民楼，东北侧为7层居民楼，西临徐东大街，南近友谊大道。支护结构为钻孔灌注桩+钢筋混凝土内支撑+立柱+冠梁及围檩结构，该基坑采用管井降水，水泥土搅拌桩作截水帷幕。图3为基坑周边环境平面图。

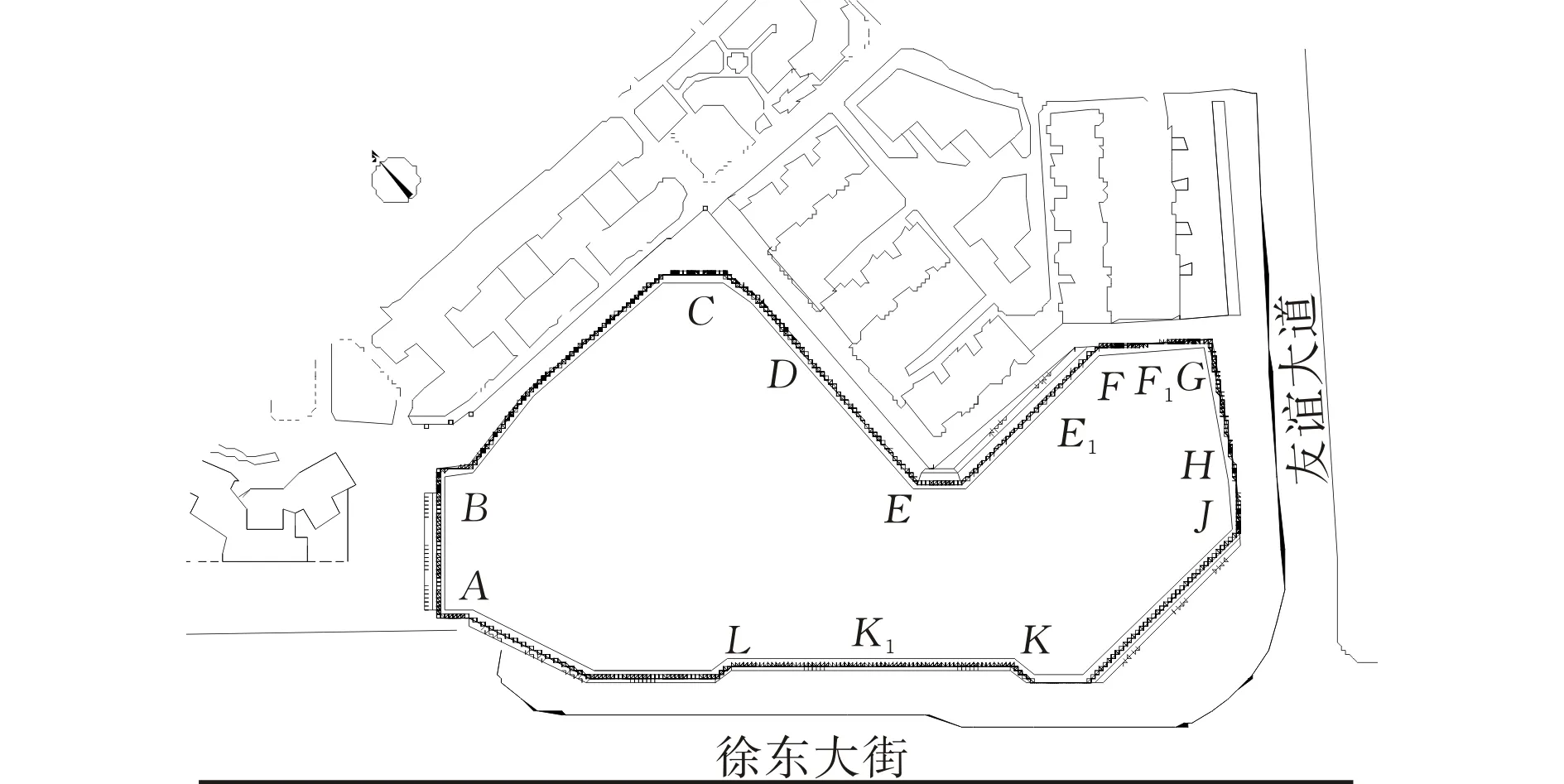
图 3 基坑周边环境平面图

3.2 有限元计算模型

运用 Midas-GTS NX有限元软件建立了分层开挖与支护的三维有限元模型，基坑的影响区域一般为开挖深度的3～5倍，取模型尺寸为300 m×200 m×45 m。该基坑的模拟分三个工况进行，工况1：基坑开挖至-2.50 m,并于-2.00 m位置处架设第一道内支撑；工况2：基坑开挖至-7.50 m,并于-7.00 m位置处架设第二道内支撑；工况3：基坑开挖至底标高-12.10 m。其中土体采用实体单元，内支撑和立柱采用梁单元，支护桩按照等刚度原则等效为地下连续墙，采用板单元模拟。模型边界条件为四周水平单向约束，底端固定约束，地表为自由边界。考虑基坑周边各类荷载为均布荷载，取临时施工荷载15 kN/m2，交通荷载取最大值50 kN/m2，地面建筑按每层15 kN/m2取值，基坑三维有限元模型如图4所示。

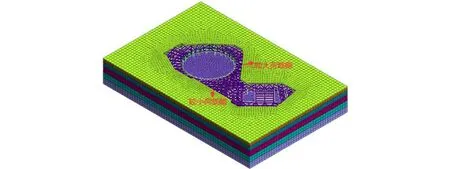
图 4 基坑三维有限元模型

3.3 计算参数的选取

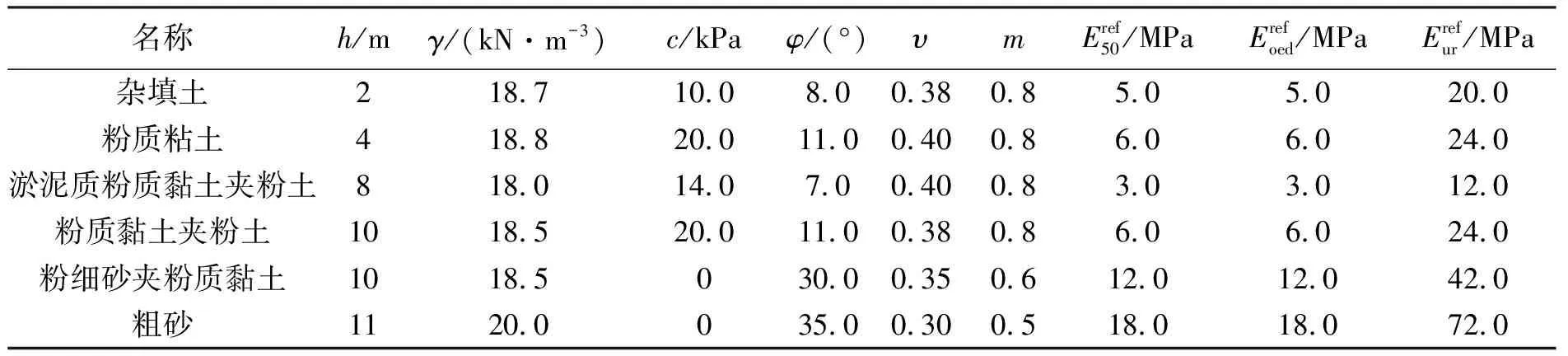
表1 土层力学参数取值

4 计算结果分析

监测数据表明，在不对称荷载作用下基坑东北侧即CE区段维护结构水平位移达到最大值，故为基坑施工过程中最危险区段。现将该区段作为研究对象，以有限元程序计算结果为依托，通过公式Kh=P/δ可计算出被动区等效水平抗力系数Kh值，由此探究在施工过程中不规则基坑形状、不对称荷载和被动区加固等因素对Kh变化规律的影响。

4.1 不规则基坑形状对Kh的影响

基坑工程的空间效应主要表现为坑角效应，尤其是几何形状不规则的基坑工程其阴角、阳角效应尤为明显。因武汉君临天下A地块基坑东北侧CE区段长度L:75.18 m,开挖深度H:12.1 m,L/h=6.213>6,故可取基坑平面应变比等于1[12]，即基坑东北侧CE区段中部围护结构的变形可等效为平面应变状态，忽略坑角效应的影响。为探究被动区等效水平抗力系数Kh值的空间分布规律，选取该区段的阴角、阳角和平面应变位置来反映Kh的分布情况。

Kh值在各位置处随土层深度的变化曲线如图5、6所示。

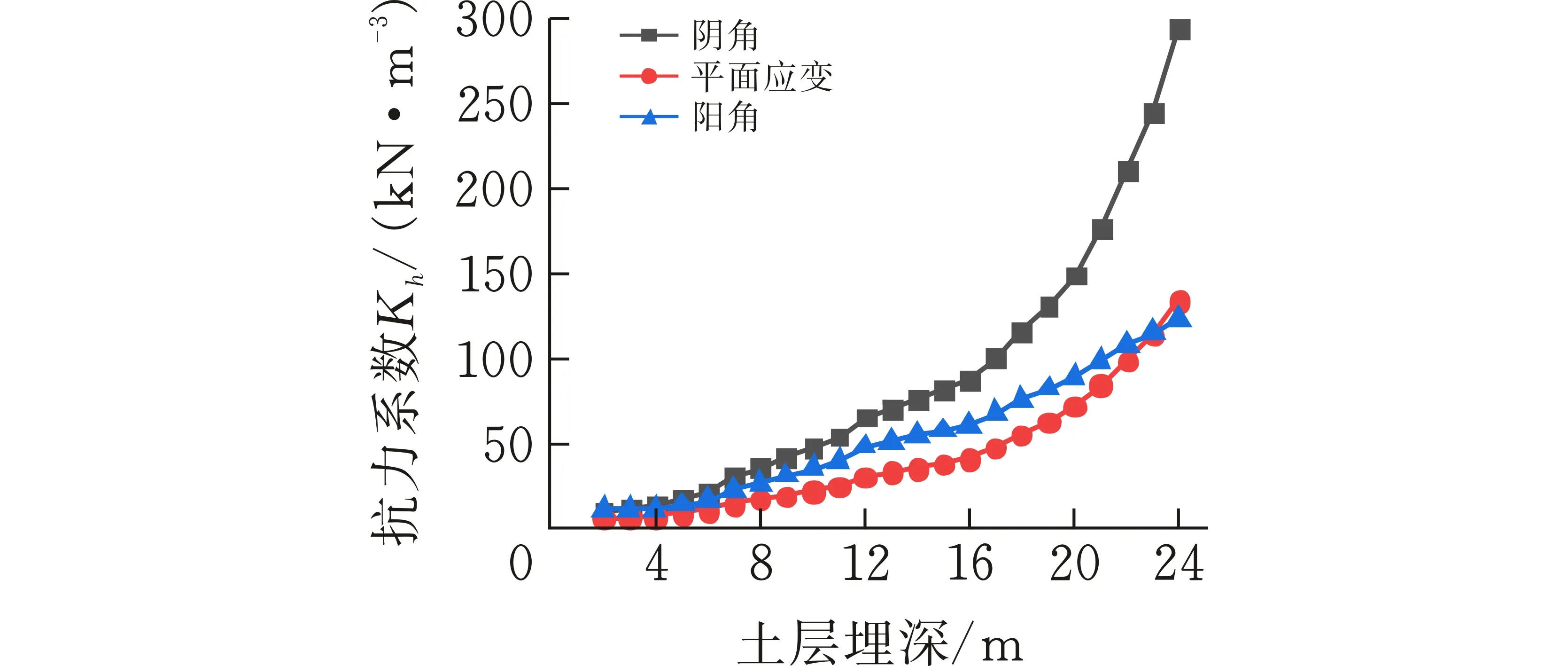
图 5 不同空间位置上Kh值随土层深度变化曲线

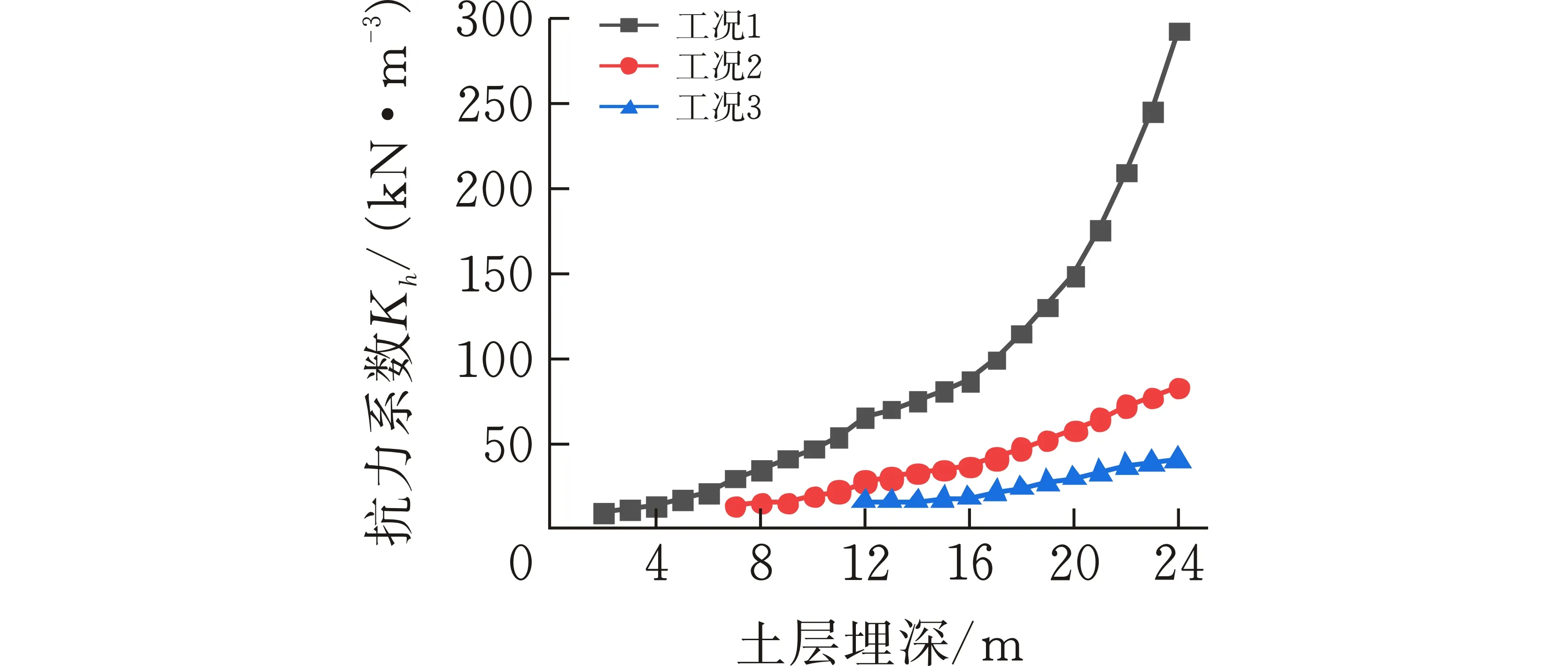
图 6 CE段中部截面Kh值随土层深度变化曲线

由图5可知，在不同空间位置上，Kh值总体变化都随土层埋深的增加而增大，变化趋势基本相同，但位于同一土层深度处Kh值的大小存在差异，在土层24 m深度处阴角、平面应变、阳角位置最大值分别为293.55×103kN/m3，134.38×103kN/m3，123.19×103kN/m3，整体上Kh值在阴角处最大、阳角次之、平面应变位置最小。这与基坑角部角度大小有关，角度越小，坑角部位相邻墙体与周围土体的相互约束作用就越显著，进一步抑制了挡墙和土体位移的发展，致使位于同一埋深不同角部处的被动区土体抵抗变形的能力存在差异。基坑CE区段的中部即平面应变位置相较于其它角部Kh值处于较低水平，为该基坑最危险断面，其Kh值的变化情况如图6所示。图6反映出了随工况的进行Kh值随土层埋深增大的幅度逐渐减小。其中工况1的Kh值从2 m处的5.949×103kN/m3陡增到24 m处的134.388×103kN/m3增幅高达2159%，而从工况3曲线来看，在12 m处Kh值为4.773×103kN/m3，22 m处增加到27.925×103kN/m3增幅降为485%。

4.2 不对称荷载对Kh的影响

基坑荷载的不均匀分布将导致基坑挡墙的非对称受力与变形，致使等效水平抗力系数Kh的分布规律和随工期的衰减速率也存在明显差异。图7为较大荷载作用下的基坑东北侧区段和较小荷载作用下的基坑南侧区段中部，地下18 m处Kh值随时间的变化规律。

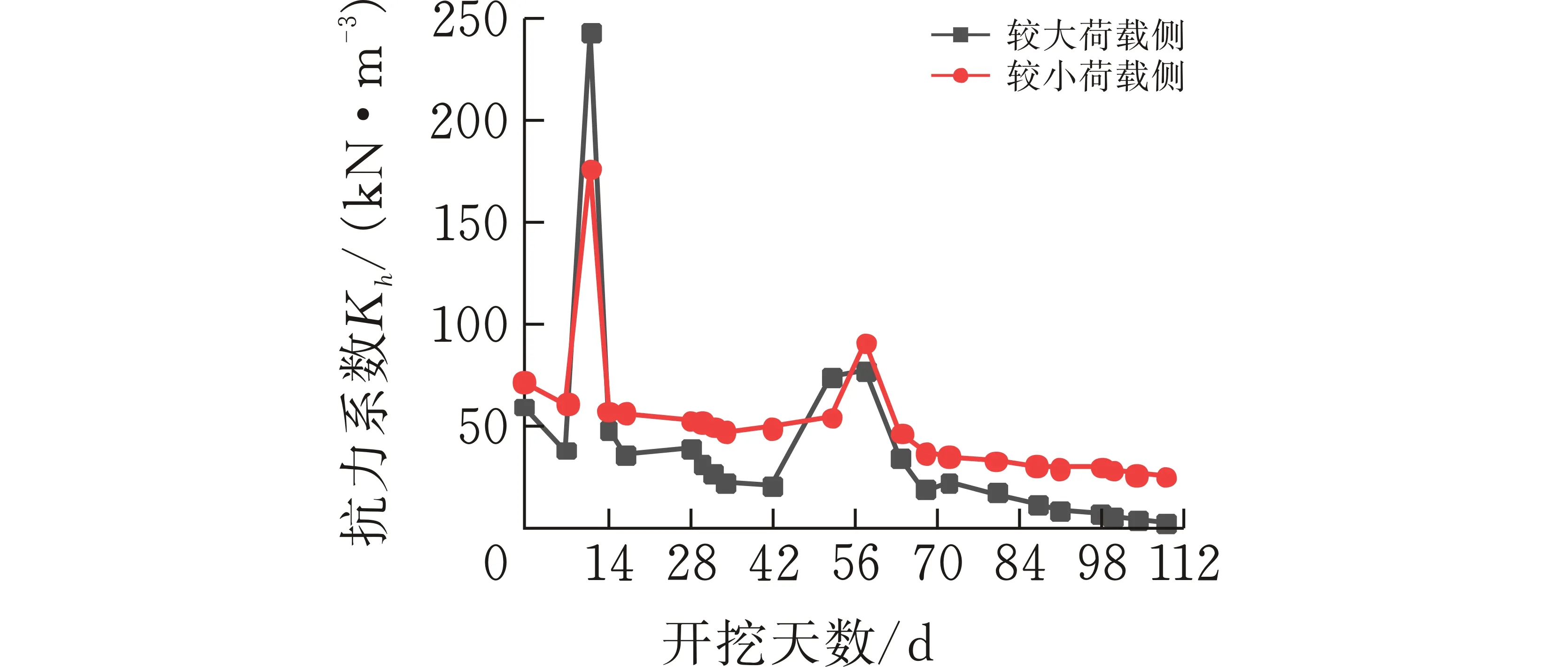
图 7 土层埋深18m处Kh值随时间的变化图

由图可见两条曲线的Kh值变化趋势大致相同，均出现了两次陡增现象，一次是在开挖后第7～11 d，另一次是在第52～58 d，其它时段随时间而减小，总体呈减小走势。较大荷载一侧Kh最大值为244.3×103kN/m3，最小值衰减至3.1×103kN/m3，较小荷载一侧最大值为177.2×103kN/m3，最小值为25.8×103kN/m3，可见衰减幅度之大。

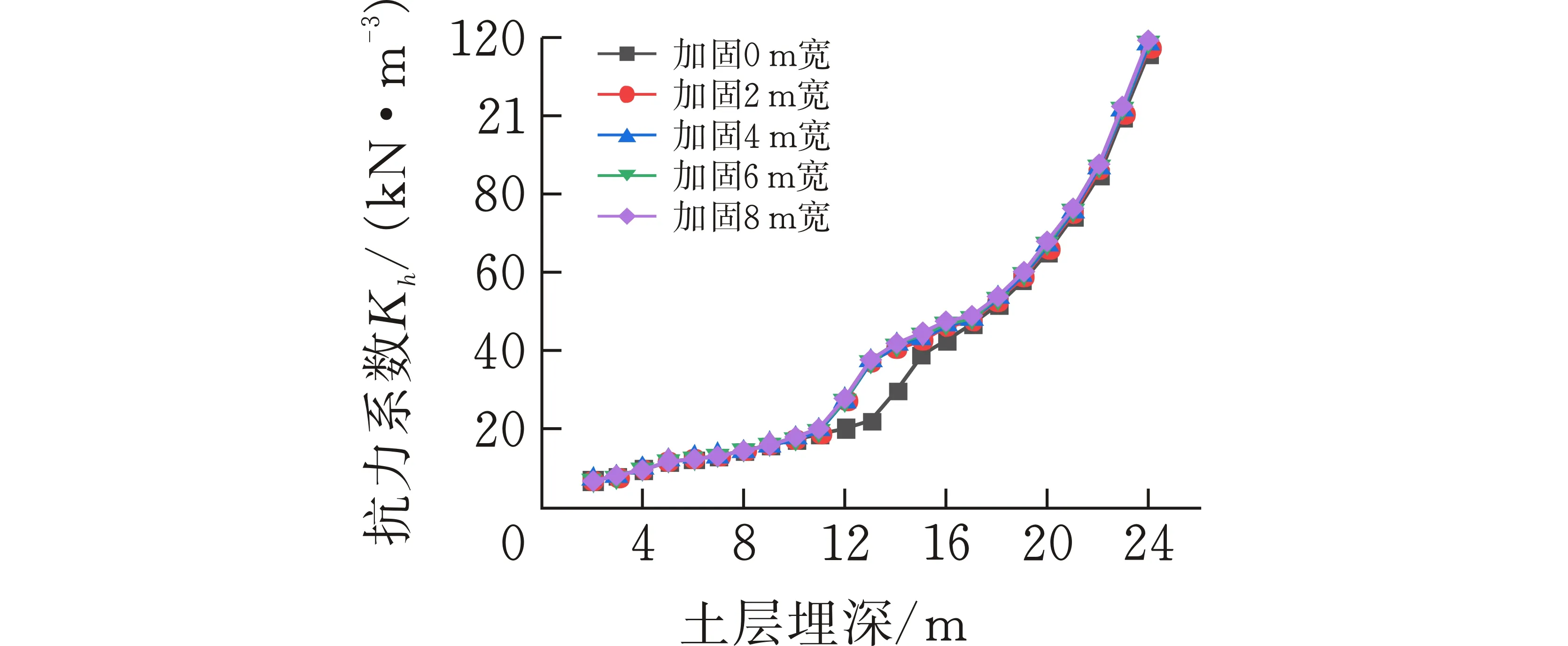
(a)加固宽度对Kh值的影响

在工况的推进过程中，因各种施工扰动损伤了土体结构，且软土基坑土体具有显著的流变性，非对称荷载作用下的土体，高应力一侧相较于低应力一侧，土体的流变速率较大，进而加速了Kh值的衰减。Kh值衰减幅度一般表现为高应力一侧大于低应力一侧、开挖前期大于开挖后期。施工过程中某些时段Kh值出现了跳跃式增长，该现象可能是由于内支撑的突然架设，使得围护结构的位移大幅减小，但被动土压力减小幅度较小所致。

基坑被动区加固将有效提高被动区土体的弹性模量，增强坑内土体对围护结构的被动土压力，以减小围护结构的变形，进而使得被动区土体的等效水平抗力系数相应提高。图8a和b分别为Kh值随被动区土体加固宽度和加固深度的变化图，结果表明加固宽度的变化对Kh值无明显影响，其值主要受加固深度的影响，在进行一定深度的加固后，Kh值有显著的提高，其提高的深度区间为加固区域上层表面以上1 m至下层表面以下1 m的深度范围，如图中所示加固深度为4 m，加固土体位于土层12～16 m时，Kh值的变化区间扩展至土层11～17 m的深度范围，使长达6 m范围深的土体被动抗力显著提高，在加固土体中部位置14 m深度处Kh值由加固前的30.04×103kN/m3提高到41.49×103kN/m3，而处于加固影响范围之外的土体其抵抗变形的能力无明显增强，即Kh值的变化曲线与未加固工况下的变化曲线重合。

4.3 Kh值对施工的反馈

武汉君临天下A地块基坑，基坑保护等级为Ⅰ级，维护结构最大侧向位移必须控制在30 mm以内。在该区段现场施工过程中，当开挖至-7.2 m时，因未至第二道内支撑的设计标高，维护结构的水平位移迅速增大至20.3 mm,Kh值衰减至20.8×103kN/m3。为减少无支撑暴露时间，及时施加第二道内支撑，该区段采用1.6 m3反铲挖掘机由基坑西侧向东侧进行盆式开挖，同时完成内支撑与开挖区域内的井字接头和中间撑的施工，在盆式开挖外侧按原施工计划分块开挖坑壁土体。并将该区段的监测次数由一天1次增加至一天2次，实测数据显示第二道内支撑及时施加后，有效阻止土体被动抗力的损失，挡墙位移迅速减小至15.6 mm，达到了预期控制指标。

5 结束语

以武汉君临天下A地块基坑工程为依托，结合现场实测数据与有限元计算结果，分析了在基坑开挖过程中各类因素对Kh值变化规律的影响。主要结论如下:

1)对于几何形状不规则的基坑，Kh值的变化具有显著的三维空间效应，即在基坑阴角处最大、阳角处次之、平面应变位置最小。

2)由于软土基坑土体具有流变性，且不对称荷载作用将加速土体的流变速率，致使Kh值呈现出随时间衰减的趋势，一般表现为较大荷载作用的土体Kh值衰减速率大于较小荷载作用的土体、基坑开挖初期衰减速率大于开挖后期。

3)在开挖后某些时段，Kh值有明显反弹，该现象主要归因于内支撑架设后，围护结构的水平位移迅速减小而被动土压力减小较少。基坑被动区土体的加固宽度对Kh值无明显影响，而通过增加加固深度可使Kh值增大。