一类三角模糊数优性组合预测模型

谢小军，马 虹，薛申芳，乔希民

一类三角模糊数优性组合预测模型

谢小军1，*马 虹2，薛申芳1，乔希民1

（1.广州工商学院，广东，广州 510850；2.广东金融学院，广东，广州 510521)

将三角模糊数序列的三个界点转换为等价的面积型中心、面积型散度、质心三个指标序列。结合广义诱导有序加权平均（GIOWA）算子，选择面积型中心、面积型散度、质心三个指标的L2范数作为最优准则，建立了一类新的三角模糊数优性组合预测模型，并证明了新提出的模型一定是优性组合预测模型。通过实例分析对比，也进一步验证了该模型是有效性和可行性，能够有效提高预测精度，最后并针对GIOWA算子中的参数进行了灵敏度分析。

L2范数；三角模糊数；GIOWA算子；组合预测模型

0 引言

随着社会经济的不断发展，导致事物系统不确定性增强从而更具模糊特征，三角模糊数成为了刻画不确定信息的一种常见表达形式。最近几年，组合预测模型得到迅速的发展，国内外学者也积累了大量的研究成果[1-7]。因此，构建基于三角模糊数的组合预测模型符合事物的实际发展趋势，研究三角模糊数组合预测模型既具有理论意义也具有现实意义。目前，针对三角模糊数的研究才刚刚起步，主要从三角模糊数序列的本身数据的特点出发和预测方法上进行了理论研究与创新。1）利用单一预测模型对三角模糊数进行建模。文献[8]将三角模糊数序列三个界点序列用对应的面积序列、重心序列、中界点序列三个指标数序列替换，利用转换后的序列构建灰色预测模型，最后再利用公式进行还原。文献[9]在文献[8]研究基础上构建了基于支持向量机的三角模糊数预测模型。文献[10]通过改进GM(0,N)模型方程的参数设置，并结合马尔科夫预测和序列转换方法对模型的预测序列进行修正，构建了基于GM(0,N)模型的三元区间数序列预测模型。文献[11]在文献[8]的基础上构建了基于神经网络的三角模糊数预测模型，并结合遗传算法进一步进行了优化。2）利用组合预测模型对三角模糊数进行建模。文献[12]基于对称三角模糊数，将对称三角模糊数的覆盖面积和重心指标进行替代，建立了相应的基于IOWA算子的三角模糊数组合预测模型，以面积序列和重心序列的相关系数的为最优准则，并引入重要性参数将其转化为单目标规划模型。文献[13]引入广义诱导有序加权平均算子，构建了基于对称三角模糊数及GIOWA算子的组合预测模型。文献[14]定义了三角模糊数左右区间概念，提出了一种区间相似度的度量公式，将三角模糊数左右区间的相似度作为最优准则的度量指标，并引入诱导有序加权几何平均算子（IOWGA），建立了基于区间相似度的IOWGA算子的变权系数三角模糊数组合预测模型。文献[15]基于三角模糊数面积型中心、面积型散度、质心三个指标的基础上，建立三角模糊数预测有效度的概念，提出了一种新的基于三角模糊数的预测有效度最优的组合预测模型。文献[16]将三角模糊数以面积型中心、面积型散度、质心三个指标进行描述，然后引入诱导有序加权几何平均算子（IOWGA）算子，并以面积型中心、面积型散度、质心三个指标的对数误差为最优准则，提出了一种基于对数误差的IOWGA算子的三角模糊数变权组合预测模型。

基于已有研究基础，提出了一类新的基于L2范数的GIOWA算子的三角模糊数优性组合预测模型。新建立的模型选择以三角模糊数的相似度作为GIOWA算子的诱导值，以三角模糊数基于面积型中心、面积型散度、质心三个指标的L2范数作为最优准则，并通过引入偏好系数将多目标优化问题转换为单目标优化模型。最后通过实例分析验证了该模型的有效性，并从理论上进一步证明了本文提出的模型一定是优性组合预测模型。已有研究成果大多数是将针对对称三角模糊数，本文提出的组合模型可适用性更广，可对普遍三角模糊数进行建模。

1 理论基础

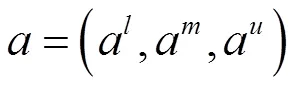
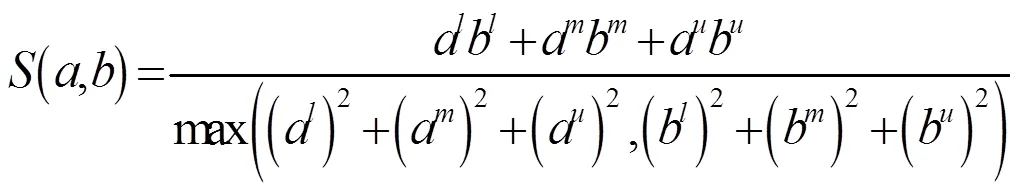
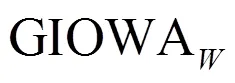
2 组合预测模型的建立

定义4 令:

定义5 令：

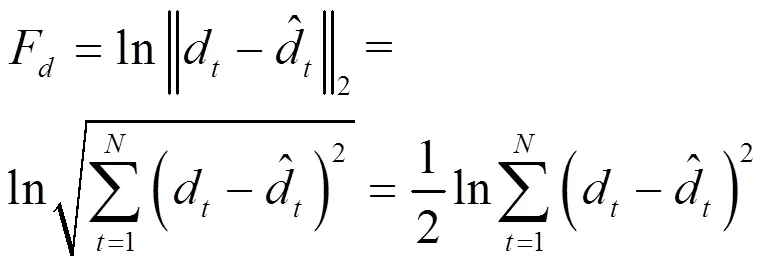
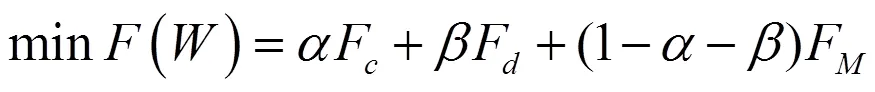
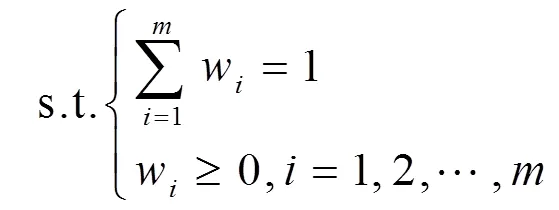
定义6 设

定理1 若基于L2范数的三角形模糊数组合预测模型（12）中，求得的最优解中若至少有两种单项预测方法是有效的，则构建的组合预测模型一定是优性组合预测模型。

所以

则由定义6可知定理1成立。

3 实例分析

为了验证本文提出的一列三角模糊数变权组合预测模型的有效性，以文献[12]的原始数据和单项预测方法的结果为研究基础进行实例分析，原始数据和各单项预测方法的预测结果见表1。

表1 实际三角模糊数序列与三种单项预测方法拟合预测结果

Table 1 Fitting prediction results of actual triangular fuzzy number series and three single prediction methods

原始数据方法1预测结果方法2预测结果方法3预测结果 1(66.3,72.5,78.7)(69.667,75.753,81.83963)(66.1571,72.3747,78.5923)(66.3,72.5,78.7) 2(67.9,74.3,80.7)(66.414,72.6894,78.9649)(69.6027,76.211,82.8193)(67.9,74.3,80.7) 3(71.6,78.5,85.4)(71.7608,78.644,85.5274)(73.0483,80.0473,87.0463)(70.754,77.41,84.061) 4(76.4,83.8,91.2)(74.737,81.9153,89.0933)(76.4939,83.8836,91.2733)(73.98,81.0646,88.149) 5(79.8,87.6,95.4)(82.128,89.2122,96.2967)(79.9395,87.7199,95.5003)(78.673,86.2824,93.892) 6(84.8,93.1,101.4)(83.416,91.558,99.6995)(83.3851,91.5562,99.7273)(82.679,90.739,98.7994) 7(86.9,95.5,104.1)(87.1476,95.724,104.299)(86.8307,95.3925,103.9543)(87.426,95.979,104.533) 8(93.4,102.7,112.0)(94.777,,104.17,113.565)(90.2763,99.2288,108.1813)(90.536,99.467,108.398) 9(94.9,104.3,113.7)(96.077,105.638,115.193)(93.7219,103.065,112.4083)(95.98,105.522,115.062) 10(99.3,109.2,119.1)(95.712,105.228,114.744)(97.1675,106.901,116.6353)(99.12,108.95,118.7852) 11(99.5,109.4,119.3)(101.651,111.822,121.99)(100.613,110.738,120.862)(102.83,113.06,123.295) 12(102.7,113.3,123.9)(102.22,112.454,122.686)(104.059,114.574,125.089)(104.35,114.74,125.131) 13(105.3,115.9,126.5)(105.115,115.686,126.25)(107.504,118.41,129.3163)(106.77,117.678,128.58)

表2 单项预测方法各时点面积指标、中界点，重心指标序列的预测精度

Table 2 Prediction accuracy of area index, middle boundary point and center of gravity index series at each time point of single prediction method

10.95730.99831.0000(66.3,72.5,78.7)(66.157,72.375,78.592)(69.667,75.753,81.84) 20.97830.97491.0000(67.9,74.3,80.7)(66.414,72.689,78.965)(69.603,76.211,82.819) 30.99820.98070.9860(71.761,78.644,85.527)(70.754,77.408,84.061)(73.048,80.047,87.046) 40.97750.99900.9673(76.494,83.884,91.273)(74.737,81.915,89.093)(73.98,81.065,88.149) 50.98240.99870.9849(79.939,87.72,95.5)(78.673,86.282,93.892)(82.128,89.212,96.297) 60.98340.98340.9746(83.385,91.556,99.727)(83.416,91.558,99.7)(82.679,90.739,98.799) 70.99770.99890.9951(86.831,95.392,103.95)(87.148,95.724,104.3)(87.426,95.979,104.53) 80.98590.96620.9685(94.777,104.17,113.56)(90.536,99.467,108.4)(90.276,99.229,108.18) 90.98730.98820.9884(95.981,105.52,115.06)(93.722,103.07,112.41)(96.077,105.63,115.19) 100.96360.97900.9977(99.119,108.95,118.79)(97.168,106.9,116.64)(95.712,105.23,114.74) 110.97830.98790.9676(100.61,110.74,120.86)(101.65,111.82,121.99)(102.83,113.06,123.3) 120.99240.98900.9876(102.22,112.45,122.69)(104.06,114.57,125.09)(104.35,114.74,125.13) 130.99810.97880.9848(105.11,115.69,126.25)(106.77,117.68,128.58)(107.5,118.41,129.32)

表3 本文组合模型对应的最优权系数

Table 3 The optimal weight coefficient of the combined model in this paper

本文组合模型权系数 0.7995150.1920180.008466 0.8005650.1994350 0.7988410.2011590 0.7908210.2091790 0.7823070.2176930 0.7576050.2423950

1）有效性分析

表4 本文组合模型与各单项预测方法预测效果评价指标

Table 4 prediction effect evaluation indexes of combined model and single prediction method in this paper

预测模型MSELMSEMMSEUMSEL 单项方法11.02140.46421.38202.8676 单项方法21.13590.46820.83852.4426 单项方法32.08680.52663.28555.8989 文献[12]方法0.20730.22050.23520.6630 本文0.17020.19610.22360.5899 本文0.16930.19510.22250.5869 本文0.16960.19530.22270.5876 本文0.17100.19650.22360.5911 本文0.17170.19700.22400.5927 本文0.17320.19830.22510.5966 预测评价指标公式

由表4可知：本文所提出的基于L2范数的GIOWA算子的三角模糊数变权组合预测模型的四个指标、、、数值都远小于所有单项预测方法，因此，本文提出的组合模型能够显著提高三角模糊数的预测精度。

与文献[12]组合模型对比，本文提出的L2范数的GIOWA算子的三角模糊数变权组合预测模型四个指标、、、数值也都均小于文献[12]的方法，且本文提出的组合模型可适用普遍三角模糊数序列的建模，可应用性更广，故本文提出的模型是有效的。

2）参数的灵敏度分析

图2 时最优权重随的变化

4 结论

文章基于已有的研究成果，将三角模糊数的三个界点序列用等价的面积型中心、面积型散度、质心三个指标序列进行替换，通过结合广义诱导有序加权平均（GIOWA）算子，以基于面积型中心、面积型散度、质心三个指标的L2范数作为最优准则，建立了一类有效的三角模糊数变权组合预测模型，解决了对三角模糊数三个界点直接建模可能产生跳跃的问题，并且克服了组合模型定权的缺点，本文模型更加灵活，鲁棒性更强，可适用性也更加广泛。并且通过实例分析也进一步验证了模型的有效性，通过对比试验表明，本文提出的模型可以有效提高三角模糊数的预测精度。后期进一步工作可讨论不同的单项预测方法对组合预测模型的影响。

[1] Lu J.Gray system theory and residual corrected model Combination forecasting of long-term power load[J]. Electrical Engineering,2013,14(7):7-10.

[2] Peng X Y,Zhang B, Cui Y Q.The short-term load forecasting of electric power system based on combination forecast model[C].2015 27th Chinese Control and Decision Conference(CCDC). IEEE,2015.

[3] Li W Q ,Li C.A combination model with variable weight optimization for short-term electrical load forecasting[J].Energy,2018,164:575-593.

[4] 丁珍妮,陈华友,朱家明.基于面积型中心误差准则的模糊组合预测模型及应用[J].模糊系统与数学, 2018，32(3):169-179.

[5] 谢小军,邱云兰,时凌.基于ARIMA和BP神经网络组合模型的能源消费预测[J].数学的实践与认识, 2019，49(10):292-298.

[6] 袁宏俊,胡凌云.基于连续区间有序几何加权平均Power算子的区间型组合预测模型[J].数理统计与管理,2019，38(2):270-280.

[7] 陶志富,葛璐,璐陈华.基于滑动窗口的一类非负可变权组合预测方法[J].控制与决策，2020，35(6):1-7.

[8] 曾祥艳,舒兰,蒋贵荣,等.基于三角模糊数序列的灰色预测模型[J].数学的实践与认识, 2012,42(19):109-114.

[9] 刘齐林,曾玲,曾祥艳.基于支持向量机的区间模糊数时间序列预测[J].数学的实践与认识,2015, 45(22):207-214.

[10] 曾祥艳,王燕,何芳丽,等. 基于GM(0,N)模型的三元区间数序列预测[J].控制与决策,2020,35(9):2269-2276.

[11] 谢小军,马虹,杨付贵,等.一种新的区间模糊数时间序列预测模型[J].曲阜师范大学学报:自然科学版,2020,46(4):72-76.

[12] 张宇菲,陈华友.基于面积和重心预测精度的IOWA算子的模糊变权组合预测模型[J].统计与决策,2018(14):24-28.

[13] 杜康,袁宏俊,郑亚男.基于三角模糊数及GIOWA算子的区间型组合预测模型[J].统计与决策,2019(16):22-28.

[14] 谢小军,马虹,朱宁,等，基于区间相似度的IOWGA算子的三角模糊数组合预测模型[J].统计与决策,2020(23):23-27.

[15] 张宇菲,陈华友.基于面积和重心预测精度的IOWA算子的模糊变权组合预测模型[J].统计与决策, 2018(14):24-28.

[16] 谢小军,马虹,邱云兰.基于对数误差的IOWGA算子的三角模糊数变权组合预测模型[J].汕头大学学报:自然科学版,2021,36(1):55-61.

[17] 丁珍妮,陈华友,朱家明.三角模糊数组合预测模型及其Shapley值近似解法[J].统计与决策, 2019(24):68-72.

[18] 袁宏俊,杜康,胡凌云.基于三角模糊数相似度的区间型组合预测模型[J].统计与决策,2019(6):24-29.

A SUPERIOR COMBINATION FORECASTING MODEL OF TRIANGULAR FUZZY NUMBERS

XIE Xiao-jun1,*MA Hong2, XUE Shen-fang1, QIAO Xi-min1

（1. Guangzhou College of Technology and Business, Guangzhou, Guangdong 510850, China; 2. Guangdong University of Finance, Guangzhou , Guangdong 510521, China）

The three boundary points of triangular fuzzy number sequence are transformed into three equivalent index sequences: area type center, area type divergence and centroid. Combined with the generalized induced ordered weighted average (GIOWA) operator, the L2 norm of area type center, area type divergence and centroid is selected as the optimal criterion to establish a new superior combination forecasting model of triangular fuzzy numbers, and it is proved that the new model is a superior combination forecasting model. Through the example analysis and comparison, the model is further verified to be effective and feasible, which can effectively improve the prediction accuracy. Finally, the sensitivity analysis of the parameters in GIOWA operator is carried out.

L2 norm; triangle fuzzy number; GIOWA operator; combination forecasting model

1674-8085（2022）01-0001-07

O159

A

10.3969/j.issn.1674-8085.2022.01.001

2021-06-09；

2021-07-16

国家自然科学基金项目（61572016）；广州工商学院 2021年校级科研课题（KA202132）

谢小军(1990-)，男，湖南衡阳人，讲师，硕士生，主要从事预测和决策分析研究(Email:454625759@qq.com)；

*马 虹(1989-)，女，安徽宿州人，硕士生，主要从事预测和决策分析研究(Email:junxx12@163.com).