基于改进BAS 算法的综合能源系统优化调度研究
2022-02-27撖奥洋周生奇菅学辉张智晟
赵 帅,撖奥洋,周生奇,菅学辉,魏 振,张智晟
(1.青岛大学电气工程学院,山东 青岛 266071;2.国网山东省电力公司青岛供电公司,山东青岛 266002)
近年来,能源与国家经济发展和人民生活水平的联系越来越密切,综合能源系统经济运行调度的概念应运而生。众多学者在综合能源系统领域已进行大量的研究,文献[1]建立了描述不确定性的约束,提高了高渗透率下可再生能源的利用率。文献[2]为应对环境污染问题,在双层优化模型的基础上,考虑优化多载波能量系统。文献[3]将复杂天然气潮流约束进行凸化二阶锥松弛,提升了所提模型的可求解性。文献[4]通过模型中两种不同尺度,在不显著改变运行费用的情况下满足实时负荷需求。文献[5]将多目标问题利用弹性恢复转化为单目标问题,实现区域综合能源系统优化调度。
综合能源系统结构模型复杂、优化变量较多、表达式较复杂,优化调度模型的求解是一个非线性问题。文献[6]构造了城镇综合能源系统的优化调度模型,运用改进粒子群算法(PSO)进行求解,使供能可靠性、经济性更优。文献[7]对于实际运行时未开设备通过双层优化结构,减小系统的约束,加快系统的收敛速度。文献[8]提出了一种改进NSGA_II 算法,解决了大量等式约束下的模型求解难题。文献[9]提出了含储氢装置的分布式能源系统的优化经济调度模型,通过改进粒子群算法验证了该模型的可行性。上述研究均通过优化调度,实现了综合能源的高效运行,但是收敛速度较慢,基于此该文将天牛须算法引入综合能源系统的研究中。
2017 年提出的BAS 算法是根据天牛须觅食原理设计的一种生物启发式算法,相比于传统智能算法具有全局搜索能力强、收敛速度快、运算量小、易实现等优点。BAS 算法已广泛应用到材料科学[10-11]、计算机科学[12]等领域。
综上所述,该文针对电、气、热综合能源系统建立了以最小运行成本为目标函数的优化调度模型,综合考虑各种设备出力上下限等约束条件。使用改进的BAS 算法对所建模型进行求解,验证其可行性。
1 综合能源系统优化调度模型
1.1 综合能源系统
该文构建的综合能源系统结构如图1 所示。
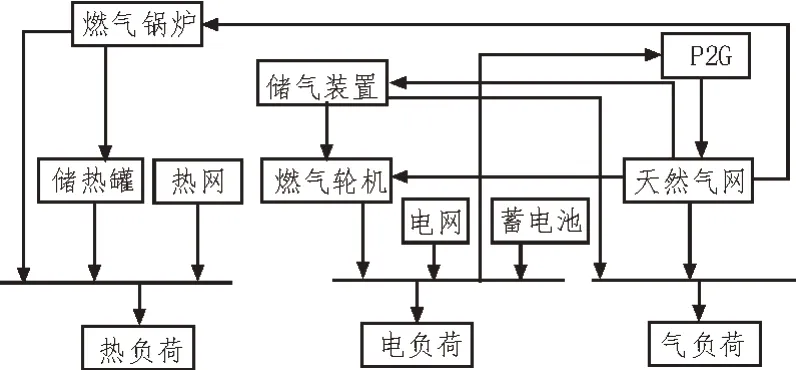
图1 系统结构
文中所构造的电力系统模型,包括储能设备、燃气轮机配合合适的算法。相比于电力系统,天然气具有可压缩的特点,天然气在管道入口和出口处的传输速度不同,在管道中通过压缩储存的天然气,称之为管存[13]。热力系统是指有蓄、放热的系统,可以用热力学和传热学基本方程对其进行描述[14]。
1.2 目标函数
通过各个能源系统的特性,构造最小成本目标函数如式(1)所示:

1.3 电力网络约束

1.4 天然气网络约束

1.5 热能网络约束
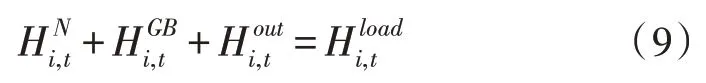

2 模型求解方法
该文对BAS 算法的改进体现在将莱维飞行策略结合到其步长的选取。
随机步长Levy(λ)表示如下:
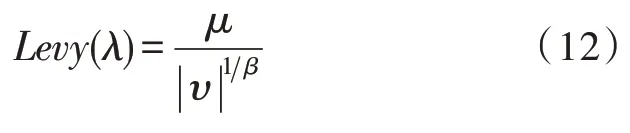
其中,λ=1+β,β∈(0,2],μ和υ服从如下高斯分布:
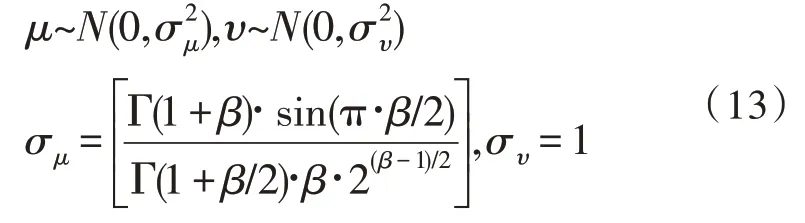
其中,Γ(·)为标准伽玛函数,该文取β=1.5。
对于每一维度下天牛和优秀个体之间的距离可表示为:

触须长度d0 可表示如下:

式中,rand(1)为产生的0~1 之间的随机数,为t时第i只天牛在第j维的触须长度。
假设天牛的位置为x,得到两须的位置:
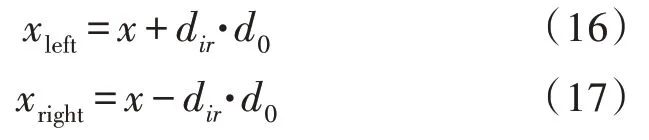
其中,xleft、xright分别为左须、右须位置;dir为随机生成[0,1]随机数的归一化值:
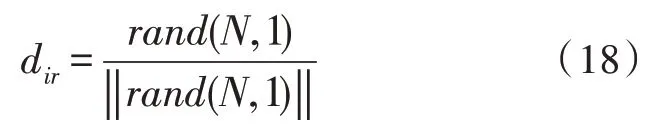
将两须位置代入到目标函数中:


其中,fleft、fright分别为目标函数左、右须值。
天牛通过向fleft、fright中较小一侧移动步长step,得到天牛位置的更新公式如下:
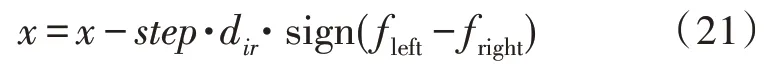
其中,step为步长取1。
改进BAS 算法步骤如下:
步骤1:输入电、气、热负荷数据,分区域初始化每个天牛的位置,设定步长1,迭代次数为100,两须间隔为0.02;
步骤2:按式(16)、(17)更新左须、右须位置,并按式(19)、(20)将两须位置代入目标函数;
步骤3:利用式(21)更新天牛位置;
步骤4:将各区域得到的新的天牛位置代入目标函数式(1),比较各区域最优值;
步骤5:判断是否满足误差需求,若满足,输出结果,反之转至步骤2。
3 算例仿真
该文所采用的综合能源系统算例主要包括GT、P2G、GB 等电气设备。采用参考文献[15]中的负荷模型和能量转换设备的转化系数,其中GT 转换效率为0.7,GB 转换效率为0.7,P2G 转换效率为0.6,利用
参考文献[16]中的分时能源价格,将最大迭代次数设置为300,天牛数目设为300。
为方便研究不同算法对综合能源系统的可行性,该文设置了4 种方案:
方案1:不考虑分时价格时,采用粒子群算法求解模型;
方案2:不考虑分时价格时,采用改进BAS 算法求解模型;
方案3:考虑分时价格时,采用粒子群算法求解模型;
方案4:考虑分时价格时,采用改进BAS 算法求解模型。
电、气、热负荷如图2 所示。
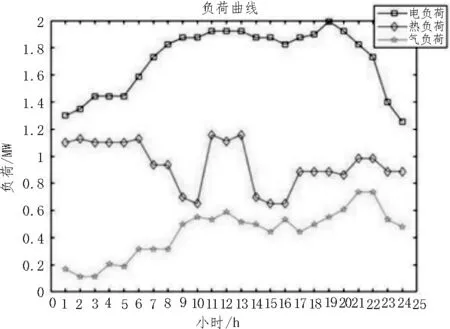
图2 电、气、热负荷曲线
电、气、热分时段价格如表1 所示。

表1 电、气、热能源各时段价格
通过仿真,总成本如表2 所示。

表2 各方案总成本
各方案的收敛速度如图3 所示。

图3 各方案优化算法的收敛速度
上述4 种方案中第4 种方案的调度方案如图4所示。
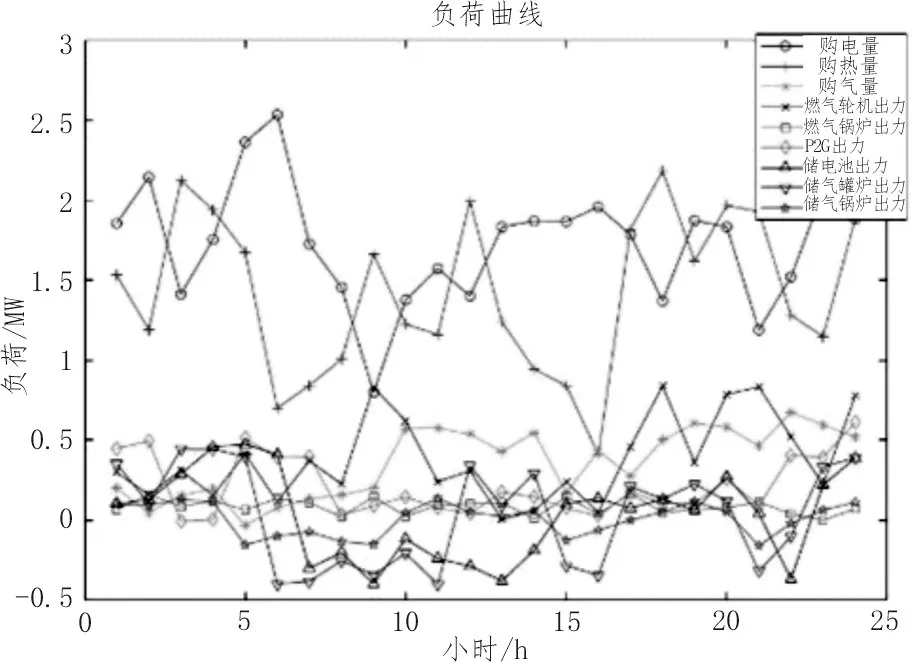
图4 方案4各设备出力调度方案
由图3 可得:对比方案1、3 和方案2、4,方案3 比方案1 节省成本3.17%;方案4 比方案2 节省成本3.51%。由此可见,实施分时价格策略时,通过粒子群算法和改进BAS 算法对综合能源系统优化调度模型的合理调度,可以有效减小系统的运行成本。对比方案1、2 可知,在不考虑分时能源价格时,方案2中运用改进BAS 算法比方案1 中运用粒子群算法节省成本1.2%,改进BAS 算法收敛速度明显优于粒子群算法。对比方案3、4 可知,方案4 中改进BAS 算法比方案3 中粒子群算法节约成本1.93%。
由图4 可知,购热和购气量在改进BAS 算法的调度下,受分时能源价格的影响较大。对于购电量,在4 h 时分时电价较低时购电量达到峰值,8~19 h 时购电量维持在略低于负荷需求量,这时需要其他电能转换设备将其他形式能量转换为电能,减少了购电量和购电成本,起到了削峰填谷的作用。对于能量转换设备和能量储存设备,受自身出力上下限的约束,维持在出力范围内波动不大[17-18]。
通过仿真验证了该文所构建的综合能源系统优化调度模型的有效性,以及改进BAS 算法在该模型求解上的可行性。
4 结论
在多种能源联系日益紧密的背景下,该文提出了一种基于分时能源价格下,针对电、气、热综合能源系统,建立了以最小成本为目标函数的优化调度模型。在综合考虑电、气、热输送量约束的基础上,同时计及各种能量转换设备出力上下限等约束条件。最后通过算例进行模拟仿真,得到以下结论:该文所构建的综合能源系统优化调度模型,减少了系统购电量,降低了购电成本,起到了一定的削峰填谷的作用;与不采取分时能源价格相比,采取分时能源价格策略有利于对能量进行优化调度,实现了减小系统运行成本的目的;该文采用的改进BAS 算法对综合能源系统优化调度模型的求解具有良好的可行性,并且在收敛精度和收敛速度方面明显优于粒子群算法,有利于提高综合能源系统的经济性。
在后续的工作中,笔者将着重于模型和目标函数的改进,进一步提高系统的经济性和稳定性。
