基于改进COA的输电线路扩容规划研究
2022-02-26张柏林史玉杰付嘉瑜史海燕
何 欣,张柏林,史玉杰,付嘉瑜,史海燕
(1.国网甘肃省电力公司电力科学研究院,甘肃 兰州 730050; 2.国网甘肃省电力公司,甘肃 兰州 730050;3.兰州理工大学电气工程与信息工程学院,甘肃 兰州 730050;)
近年来,资源差异化、电力供需不均衡、高负荷下的网络阻塞等现象的出现,使得电力资源大范围优化配置显得至关重要,而中国与周边国家扩大电网互联互通有巨大的投资潜力,因此,为指导投资,开展输电线路的扩容规划是十分必要的[1]。
从系统运行的安全性和可靠性来看,输电线路需要保持容量裕度,以便在低负荷率和紧急情况下保持足够的灵活性。为确保安全,电力调度员将尽可能调整高负荷系数线路,以平衡系统运行[2]。为了避免规划阶段后的重载运行,输电线路的负荷系数应作为输电线路扩建规划过程中的一个重要方面。因此,输电线路的剩余容量和负荷系数对电力系统规划具有重要意义。文献[3]中为确保输电线路增容运行的可靠性和安全性,基于马尔可夫链蒙特卡洛方法对输电线路增容运行后的风险进行评估,结果表明线路运行风险控制在合适的范围以内,满足电网运行和调度工程的要求,但是监测数据具有不确定性。文献[4]中提出了采用动态监测技术提高输电线路的输送容量,但是在考虑日照强度、温度等因素的情况下对数学模型的准确性和合理性要求很高,实现较为困难。文献[5]中结合混沌变量的随机遍历特性,将混沌优化算法应用于输电网非线性混合整数规划模型的优化求解,提高了剩余容量,降低了投资费用,但是安全性和稳定性却有待研究。一般情况下,混沌优化算法(COA,chaos optimization algorithm)用于求解连续变量优化问题,经修正后,可用于输电扩容规划问题的研究,我们研究分析了一种新的优化目标,即在保证投资最小化的前提下,得到输电线路负荷系数的最优分布。
1 基本输电线路扩建规划模型
直流模型的静态输电扩展规划问题的数学模型[6]描述如下:
总造价最小的目标函数:
(1)
节点功率守恒:
S×Pl+Dg=Pd,
(2)
等效网络欧姆定律:
(3)
约束条件:
|Pij|≤(nij0+nij)Pijmax,
(4)
0≤nij≤nijmax
(5)
其中:ij为i-j支路;cij为输电线路初始投资成本;ce为其余投资,包括检修等;nij为新增线路数,整变量;S为支路节点关联矩阵的转置;Pl为节点注入功率;Pg为初始潮流;Pd为负载功率;Pij为支路潮流;bij为支路电纳;nij0为支路初始线路数;Uij为支路电压降;Pijmax为支路潮流最大值;nijmax为新增线路数最大值。
上述表达满足N个安全准则(SC,security criterion)的网络结构,通常情况下采用N-1个SC来确定规划结果,即在N个SC的基础上将线路数-1,各支路在运行过程中会断开,大大增加了计算量,但是提高了安全性。
2 计算方法、边界条件及模拟可靠性验证
输电剩余容量代表了系统在紧急情况下的抗干扰能力和潮流调度能力。因此,它是衡量输电能力的重要指标,考虑输电线路的负荷系数对获得实际的规划结果具有重要意义。为了反映负荷系数对未来网络结构的影响,采用惩罚系数来满足期望的负荷系数[6-7]。剩余输电能力是从确定的扩建方案中获得的,其成本可以用每条输电线路的单位建设成本来表示。新数学模型如下(包括基本输电线路模型的条件式(2)~(5)):
总最小投资成本:
(6)
最大剩余传输容量:
(7)
折中目标函数:
F=α1×minV1+α2minT2,
(8)
输电线路剩余输电容量:
Prij=Pijmax-|Pij|,
(9)
预期线路负荷系数:
(10)
每条线路单位建设成本:
Mij=Kijcij/Pijmax,
(11)
其中:Mij为单位容量投资成本;Prij为支路剩余容量;Kij支路惩罚系数;α1、α2为权重系数;Kset为线路负荷系数(规定Kset大于0.8称为高负荷线路,Kset大于0.9称为重载线路)。
在新模型求解过程中,输电线路的剩余容量成本会随着负荷系数变化,引入惩罚函数以减少其对规划结果的影响,通过计算得到了最优负荷系数分布下的最佳网络结构。部分潜在重载线路将调整到合理水平,高负荷线路将根据网络布局和投资预算进行调整。
3 混沌优化算法
研究将混沌优化算法应用于输电规划问题,COA利用混沌变量搜索解。首先,将混沌变量映射到控制变量范围内,连续迭代直到出现最优解,混沌变量可以根据目标函数的最优方向进行调整[7],用于优化问题的COA可以描述为:
优化目标函数:
minf(X),
(12)
等号约束条件:
s.t.hi(X)=0,i=1,2,…,M
(13)
不等约束条件:
gj(X)≤0,j=1,2,…,N
(14)
产生混沌变量的方法很多。研究中使用了被广泛接受的Logistic映射方法,即
χ(k+1)=μχ(k)(1-χ(k)),
(15)
其中:μ为控制变量;χ为迭代变量向量;k为迭代次数。式(15)在μ=4时产生混沌序列,利用初值(不动点除外)可以得到不同轨道的混沌变量。输电规划问题是一个离散、非线性优化问题,而COA方法要应用于积分变量分析,必须对COA方法进行改进,采用区间划分和比较的方法,将混沌变量转化为表示可能新增加的行号的整数变量。改进后的COA流程图如图1 所示。

图1 改进混沌算法流程Fig.1 Flow chart of improved chaos algorithm
4 算例分析
利用IEEE Garver-6节点系统对输电线路扩容进行分析,该系统有6个独立节点,9条输电线路,分别对N个SC和N-1个SC下的投资模型和改进新模型进行对比分析,规划对比见表1,采用改进COA方法得到投资模型的基本结果见表2。比较2种安全准则下不同方案的投资成本与剩余传输容量,其中A、B方案采用N个安全准则,C、D方案采用N-1个安全准则。比较4种方案下的投资成本与剩余传输容量,4种方案下IEEE Garver-6系统模型分析见图2,实线为原有线路,虚线为新增加线路,图中1~6为支路点,其余数据表示线路的传输功率(MW)。
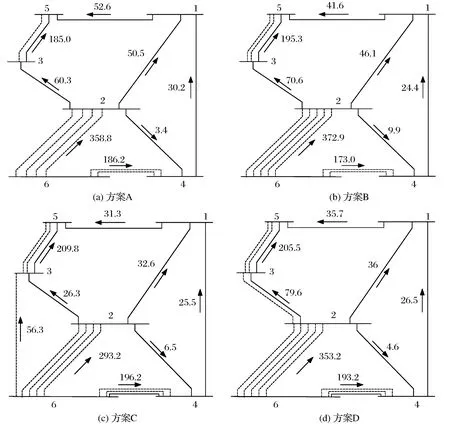
图2 4种方案下IEEE Garver-6系统Fig.2 IEEE Garver-6 system under the four schemes
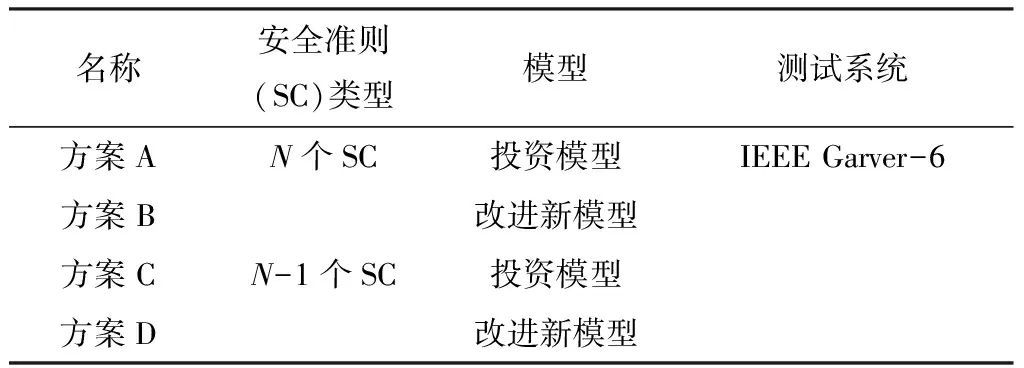
表1 规划对比说明

表2 Garver系统4种方案下的成本与剩余传输量
由以上4种方案得出的各支路在不同方案下的最大输电能力和负荷系数如表3所列。
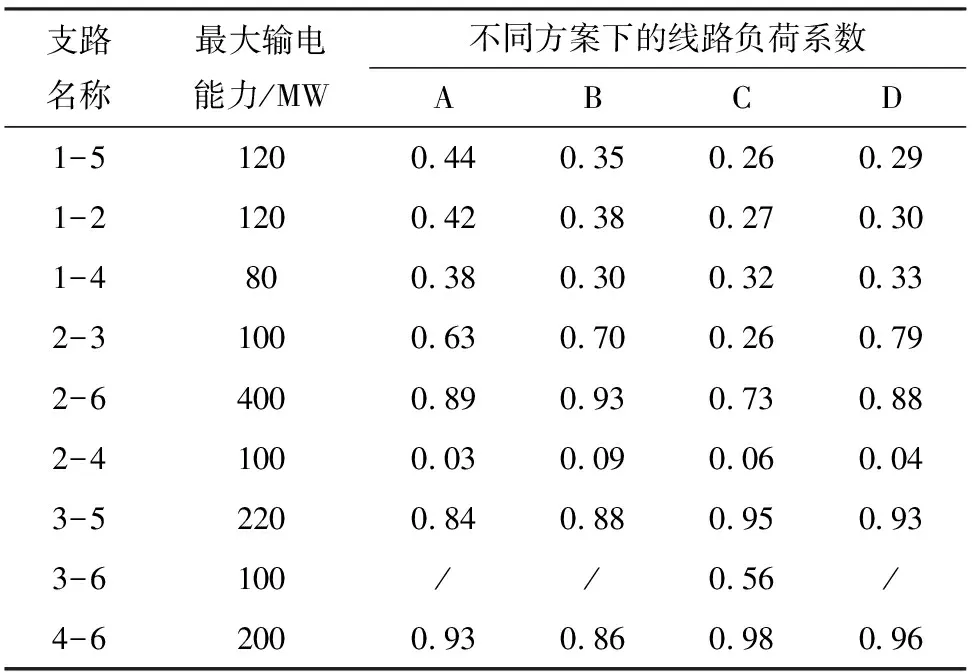
表3 Garver系统4种方案下的线路负荷系数
用负荷系数作为衡量输电线路扩容效果的指标,4种方案下线路负荷系数对比如图3所示。
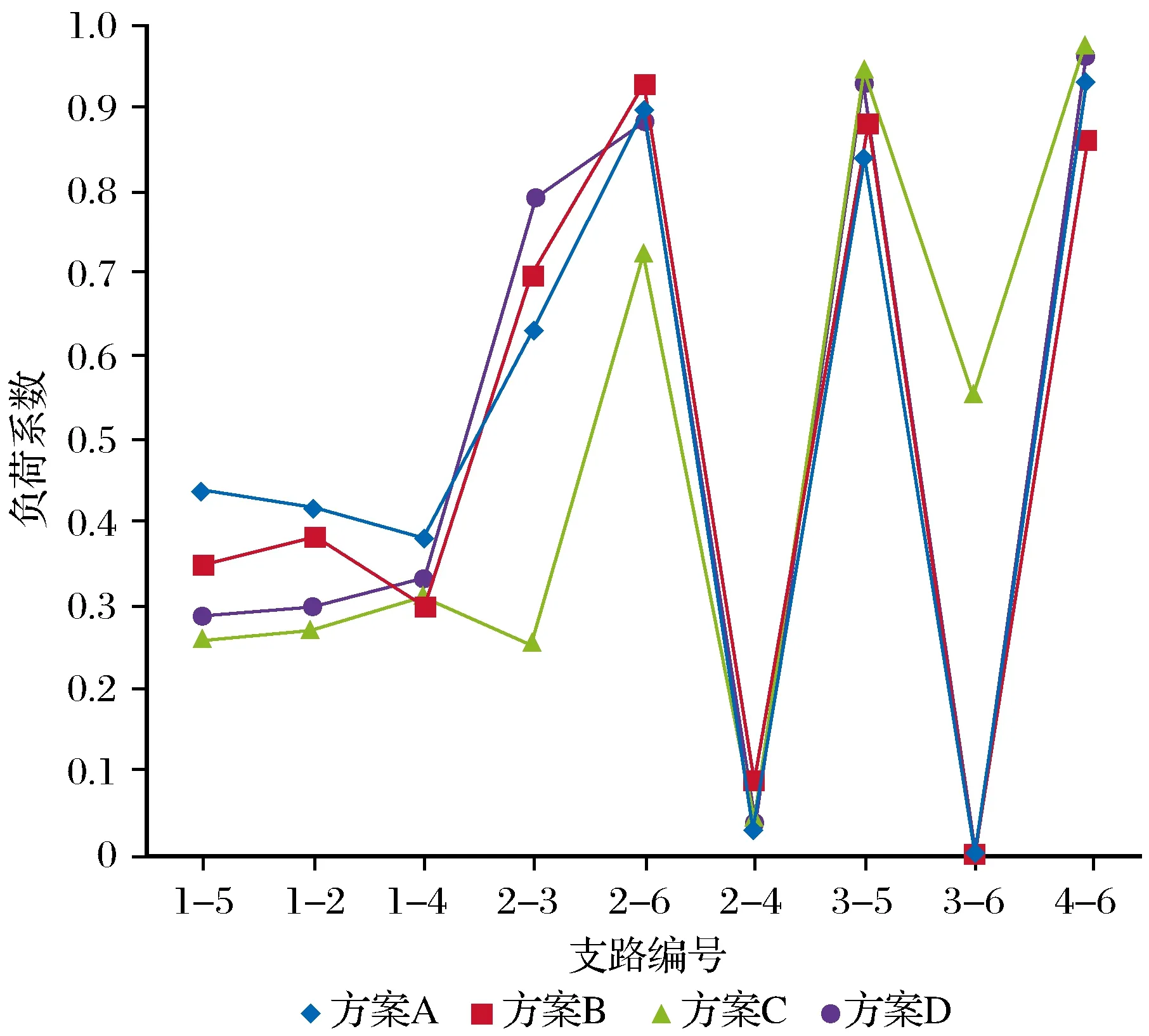
图3 4种方案下线路负荷系数Fig.3 Line load coefficient under the four schemes
以上表明,随着线路数增加,投资成本略有上升,但可以极大程度提高输电剩余容量。N个安全准则下,方案B的2-6和3-5支路的负荷系数明显比方案A大,N-1个安全准则下,方案D的2-6支路负荷系数明显比方案C大,说明相同条件下,增加线路数可以提高输电线路的承载能力,同时能增大容量裕度。
5 结论
研究提出了一种改进COA(混沌优化算法)的输电线路扩容规划策略,同时考虑投资最小化和输电剩余容量最大化,得到支路负荷系数的最佳分布,验证了该规划策略的正确性与有效性,并得到以下结论:
(1) 适当添加线路数,可以大幅提高输电剩余容量,同时投资成本略有上升。
(2) 相同安全准则下,增加线路数可以提高线路的负荷系数,即输电线路负载能力增强,容量裕度增大,极大地提高了输电线路的安全性和可靠性。
