基于IWPA优化LSSVM的输电线路接地网腐蚀预测研究
2022-02-26林肖斐夏圣峰吴簪麟张润昊
林肖斐,夏圣峰,吴簪麟,江 南,张润昊
(国网福州供电公司,福州 350000)
0 引 言
随着社会经济快速发展,电网规模不断扩大,输电线路承担的角色愈发重要,接地装置作为输电线路的重要组成部分,其安全问题不容忽视[1-3]。输电线路接地网由于常年埋于地下,运行过程中极易受土质、水和化学物质等因素影响而发生腐蚀,甚至出现断裂,严重影响雷电流导入大地[4]。因此,有必要开展输电线路接地网腐蚀预测研究工作,及时掌握接地网腐蚀情况,提高供电可靠性。
针对线路接地网腐蚀问题,文献[5]对某500 kV 输电线路接地网腐蚀原因进行分析,发现Cl-是造成接地网局部腐蚀的主要原因。文献[6]对位于接地极附近的线路接地体展开分析和研究,提出了具有针对性的防腐措施。此外,探地雷达偏移成像、电子能谱和X射线衍射等技术也被应用于接地体腐蚀检测[7-8]。文献[9]把土壤化学成分的检测结果作为接地网腐蚀速率预测模型输入量,采用RBF神经网络进行了回归,由于未对金属腐蚀的关键因子进行筛选,导致预测精度不高。文献[10]采用遗传算法(GA)优化的最小二乘支持向量机(LSSVM)对接地网腐蚀速率进行预测,并对预测结果进行误差修正,但遗传算法寻优效果差、收敛慢,不易找到全局最优值。文献[11]针对支持向量机(SVM)参数选择单一化问题,采用人工蜂群算法(ABC)优化了SVM参数,建立了基于ABC-SVM的接地网腐蚀速率预测模型,从预测结果看,计算精度有待提高。
针对上述问题,对输电线路接地网所在土壤的化学成分进行主成分分析(PCA),利用PCA找出造成线路接地网腐蚀的关键影响因子,以此确定腐蚀预测模型的输入量。采用改进狼群算法(IWPA)对LSSVM进行参数寻优,建立基于IWPA-LSSVM的输电线路接地网腐蚀预测模型,采用算例分析对模型的正确性和实用性进行验证。
1 试验及样本获取
1.1 线路接地网腐蚀试验
腐蚀试验对象为某220 kV输电线路全线接地网,该线路共计铁塔44基,全长13.2 km。在每基铁塔四个塔腿附近分别埋设规格相同的Q235金属片,埋入深度与线路接地网埋入深度相同,埋入时间为1年,1年后取出,其中埋在1号铁塔B塔腿附近金属片的腐蚀情况如图1所示。

图1 1号铁塔B塔腿附近金属片的腐蚀情况Fig.1 Metal corrosion near tower leg
根据文献[12]对所有金属片进行标准清洗,得到每基铁塔下金属片的腐蚀程度,金属片的腐蚀程度K定义如下:
(1)
式中,m0为埋入前金属片的质量,m1为每基铁塔下四块金属片经标准清洗后的剩余质量,单位均为g。
研究表明,埋在土壤中的金属受土壤pH、水、电阻率、Cl-、NO3-和氧化还原电位的作用发生腐蚀[9]。对44基铁塔附近土壤中上述6种化学成分分别进行检测和取样。土壤取样时,所有土壤均采用已编号的塑料薄膜袋密封保存,取样后立刻运回实验室,确保实验室土壤成分检测结果与现场一致。其中电阻率的现场测量如图2所示,氧化还原电位的现场测量如图3所示。

图2 电阻率测量Fig.2 Resistivity measurement

图3 氧化还原电位测量Fig.3 Potential measurement
土壤中pH值、含水量、Cl-含量和NO3-含量等测量工作在实验室完成,具体测量方法可参考文献[13],完成上述工作后,获得44基铁塔附近土壤的化学成分及对应金属片的腐蚀程度数据,样本序号为1~44,部分样本数据如表1所示。
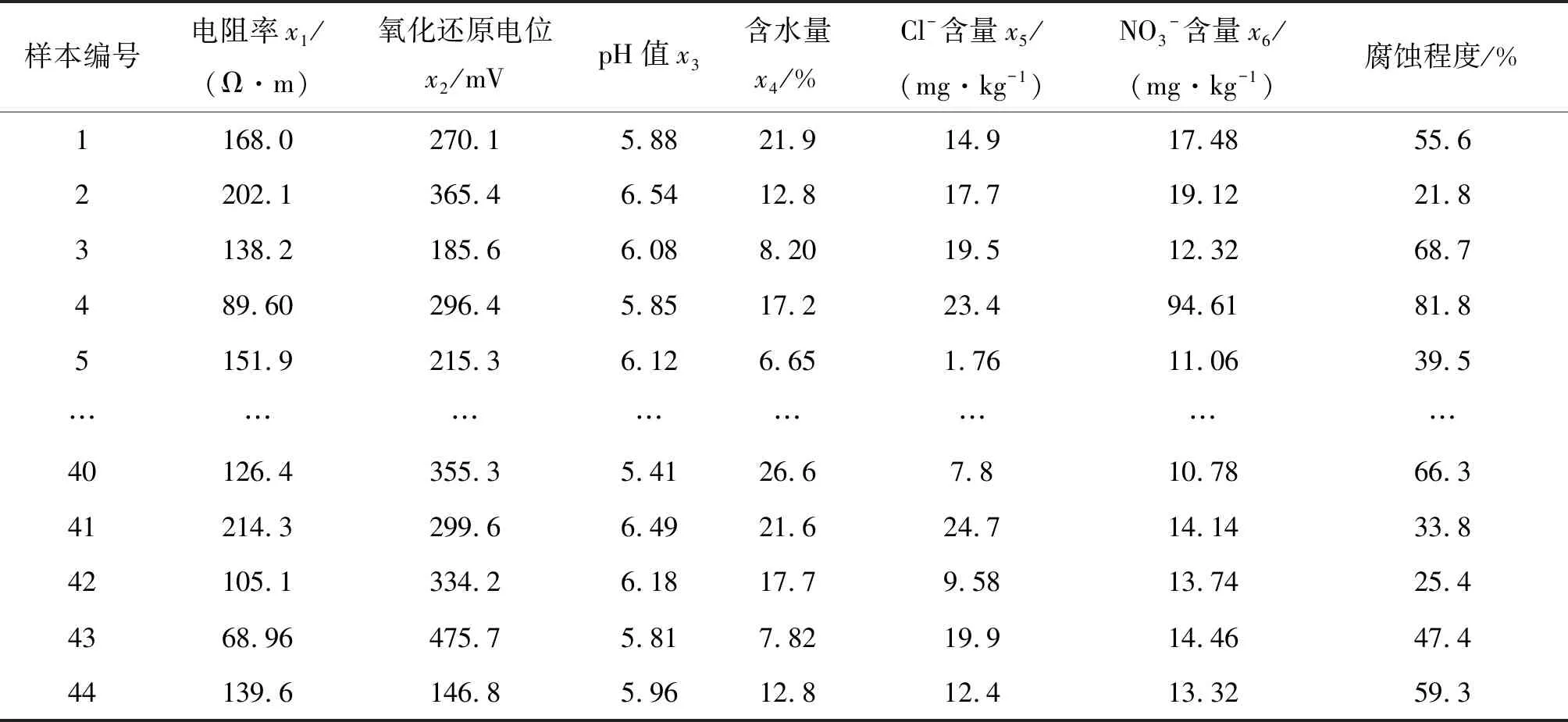
表1 部分样本数据Table 1 Sample data
1.2 主成分提取
主成分分析[14]是一种用于减小特征向量的数量、降低矩阵维数的统计方法,通过对某一事物的关键影响因子进行提取,降低回归算法的计算量,提高算法的计算速度。PCA的计算步骤如下:
1)确定分析矩阵
设有数据集X=(X1,X2,…,Xn),X中有n个样本,其中每个样本对应m维变量(受m个因素影响),则数据集分析矩阵为
(1)
2)数据归一化
归一化能够消除样本数据中不同单位、数量级之间的影响,公式如下:
(2)
式中,xi为原始值;xmax和xmin分别为xi的最大值和最小值;xi′为归一化后的数据。
3)计算协方差矩阵
令分析矩阵Xm×n归一化后得到的矩阵为X*,进而可以协方差矩阵R如下:
(3)
4)确定贡献率
根据|λI-R|=0阵即可得到特征矩阵λ,根据λ计算累计贡献率,公式如下:
(4)
利用SPSS软件对表1进行PCA分析,结果如表2所示。由表2可知,6个影响因子的排序结果为x3>x5>x6>x4>x1>x2,其中,因子x3贡献率最大,说明土壤中金属腐蚀受pH值影响最大。从累计率看,x3、x5、x6、x4的累计贡献率已超过85%,可见土壤中金属腐蚀的主要影响因子为pH值、Cl-含量、NO3-含量和含水量。
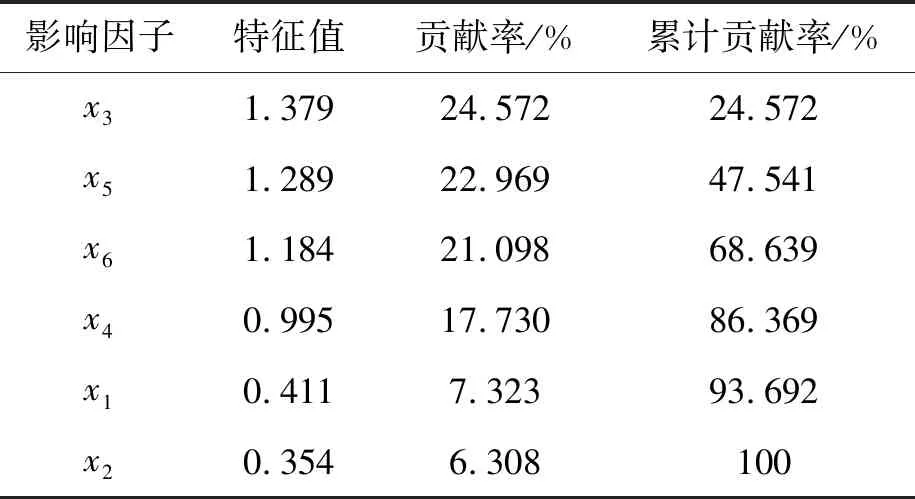
表2 各影响因子的特征值及累计贡献率Table 2 Characteristics and contributionrate of each influencing factor
2 输电线路接地网腐蚀预测模型
2.1 最小二乘支持向量机

f(x)=w*φ(x)+b
(5)
式中,φ(x)为非线性函数,w为权值向量,b为偏置量。
对于LSSVM,优化问题变为
(6)
相应约束条件为
yi[(w·φ(xi))+b]=1-ξi,i=1,2,L,…l
(7)
式中,ξi为误差,C为惩罚参数。
引入Lagrange函数,可得:

(8)
式中,α为拉格朗日乘子。
根据KKT条件得:
(9)
消去上式的w和ξi,得到线性方程组:
(10)
式中,Y=[y1,y2,…,yn]T,I=[1,1,…,1]T,Ωi,j=(φ(xi),φ(xj))=K(xi,xj),i,j=1,2,L,…,N,α=[α1,α2,…,αN]。
进而可得下列方程组:

(11)
利用最小二乘法求解b和αi,即可得到LSSVM的回归函数为
(12)
式中,K(x,xi)为核函数。
对于非线性回归,LSSVM的核函数通常采用径向基,公式为
(13)
式中,σ为核函数参数。
研究表明,惩罚参数C、核函数参数σ会直接影响LSSVM的回归拟合效果,C能够控制样本的惩罚程度,σ影响核函数的泛化能力,C和σ的寻优是建立预测模型的关键。
2.2 改进狼群算法
狼群算法(Wolf Pack Algorithm,WPA)由吴虎胜等人提出,是近年来兴起的一种寻优算法,其原理是依据狼群合作捕食获得数学上的最优解[17]。WPA中包含头狼、探狼、猛狼,它们各自的职责如图4所示。WPA的具体寻优步骤可参考文献[17]。
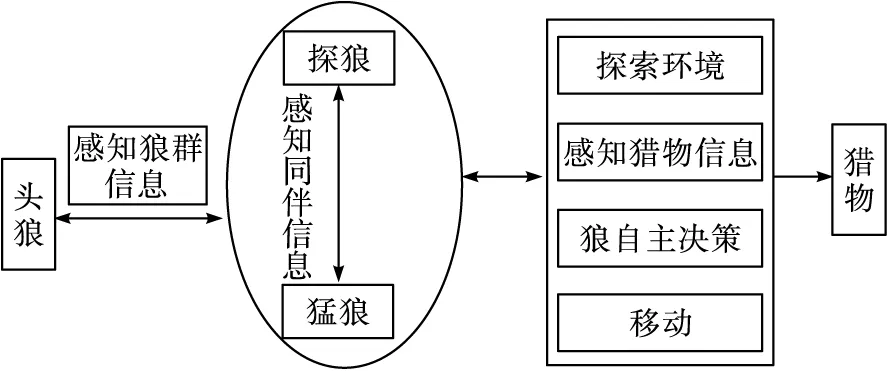
图4 狼群中各狼的职责Fig.4 Responsibility of each Wolf
相比于GA、PSO等传统优化算法,WPA的求解精度更高[18],但深入研究发现,探狼游走、猛狼围攻猎物的迭代公式仍然存在缺陷,为了达到更理想的寻优效果,本文对探狼游走行为和猛狼运动步长进行改进,形成改进狼群算法(Improved Wolf pack algorithm,IWPA),IWPA的具体改进内容如下。
2.2.1 探狼游走行为改进
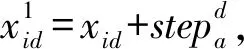
(14)
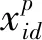
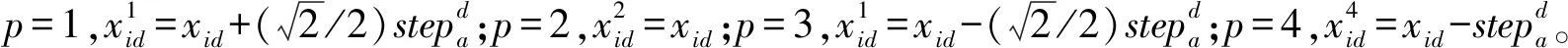
2.2.2 猛狼运动步长改进
(15)

(16)
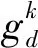
2.3 IWPA-LSSVM线路接地网腐蚀预测模型
针对LSSVM惩罚参数C和核函数参数σ的最优取值问题,本研究采用IWPA对寻找C和σ最优值,建立基于IWPA-LSSVM输电线路接地网腐蚀预测模型,模型的搭建步骤如下,流程如图5所示。

图5 输电线路接地网腐蚀预测建模流程Fig.5 Modeling procedure for corrosion prediction of transmission line grounding grid
1)根据腐蚀试验数据的主成分提取结果,将表1中的电阻率x1和氧化还原电位x2两列数据去掉,剩余5个数据列(pH值x3、Cl-含量x5、NO3-含量x6、含水量x4及其对应的金属片腐蚀程度)保持编号不变,组成新的样本数据,并进行归一化;
2)把新的样本数据分成训练集和测试集,训练集为前39组数据,用于模型训练,测试集为后5组数据,用于模型精度检验;
3)设置LSSVM的惩罚参数C、核函数参数σ的初始值,令初始值分别为C=100、σ2=2.5。
4)设置IWPA的相关参数,令人工狼数量N=100,最大迭代次数kmax=200,步长因子S=800,探狼比例因子α=4,距离判定因子ω=600,探狼游走的最大次数Tmax=20,游走方向h=4,更新比例因子β=5;
5)执行迭代,利用改进狼群算法的对LSSVM的C和σ2进行寻优,判断是否满足要求,若满足则输出最优参数,否则继续迭代;
6)将IWPA的寻优结果赋给LSSVM模型,即可完成对测试集数据的预测。
3 仿真分析
在Matlab2012a环境下进行仿真分析,以pH值、Cl-含量、NO3-含量和含水量为支持向量,采用训练集数据进行训练,利用WPA和IWPA分别对LSSVM的C和σ进行寻优,二者迭代过程如图6所示,由图6可知,WPA找到全局最优解需要进行107次迭代计算,而IWPA只需进行57次迭代即可完成寻优,可见,改进狼群算法能够有效减少迭代次数,加快收敛速度。IWPA的寻优结果为C=54.28、σ2=1.78。
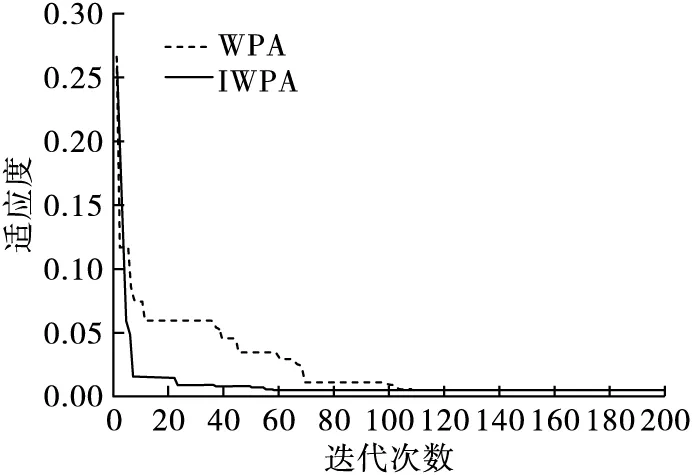
图6 WPA和IWPA迭代寻优图Fig.6 WPA and IWPA iterative optimization
为了对输电线路接地网预测模型进行评价,采用平均相对误差、全局最大相对误差和均方根误差等3种误差对模型预测效果进行综合评价,计算公式如下:
(17)
(18)
(19)
将IWPA寻找的C和σ的最优值赋给LSSVM,利用训练集对模型进行训练,结果如图7所示,由图7可知,线路接地网腐蚀预测实际值与预测值的变化趋势基本一致。训练集样本腐蚀程度预测值与实际值的绝对误差如图8所示,从图8可以看出,训练误差波动较小,经计算训练集平均相对误差为1.85%,说明IWPA-LSSVM预测模型对训练集样本的拟合度很高,训练效果较好。
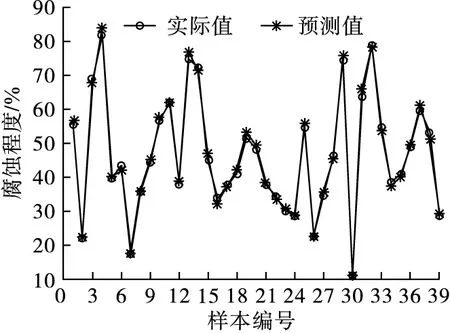
图7 模型训练效果Fig.7 Model training result
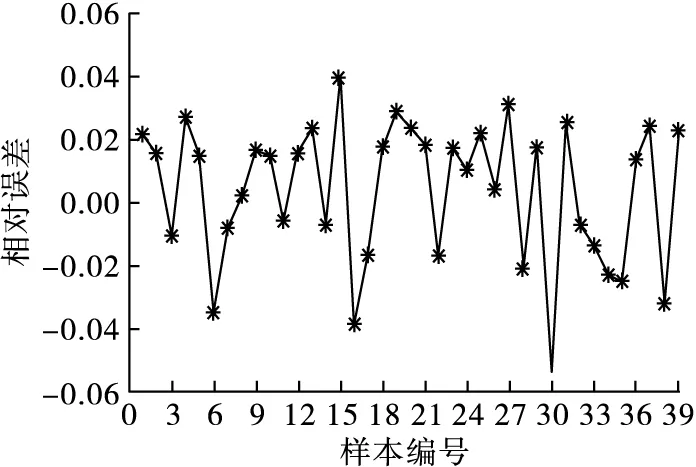
图8 训练集绝对误差Fig.8 Absolute error of training set
将测试集中的数据输入IWPA-LSSVM模型进行腐蚀程度预测,预测结果如图9所示,同时图8中也给出了WPA-LSSVM、GA-BP、PSO-SVM 3种模型的对测试集数据的预测结果,由图9可知,对比其他3种模型,IWPA-LSSVM模型的预测结果更接近输电线路接地网腐蚀程度实际值。
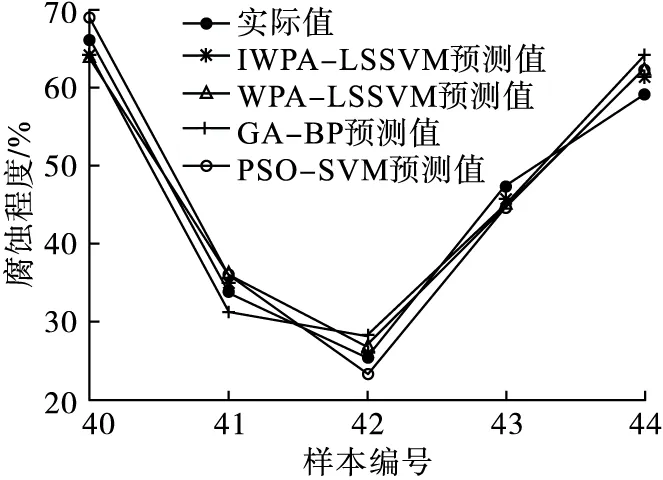
图9 4种模型腐蚀程度预测结果Fig.9 Corrosion prediction of four models
为了进一步比较4种输电线路接地网腐蚀预测模型的预测精度,表3给出了4种预测模型预测结果的各类误差,从平均相对误差上看,IWPA-LSSVM预测模型为3.47%,相比于其他模型,误差下降明显,说明改进狼群算法能够显著提高线路接地网的预测精度。从全局最大相对误差和均方根误差上看,IWPA-LSSVM预测模型分别为4.35%和0.016 4,均小于其他模型,可见IWPA-LSSVM模型外推预测的波动性更小,稳定性更好。
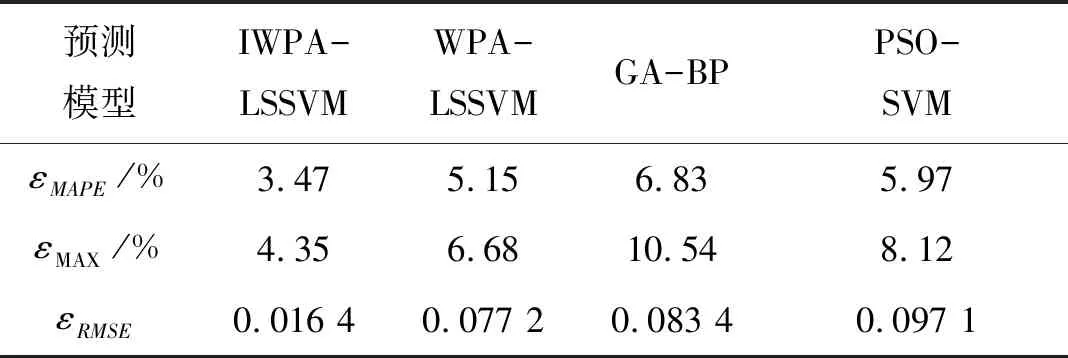
表3 4种模型预测结果误差对比Table 3 Comparison of prediction errors on four models
4 结 论
1)通过输电线路接地网腐蚀试验获得44样本数据,对样本数据进行主成分分析,确定pH值、Cl-含量、NO3-含量和含水量是土壤中金属腐蚀的主要原因,根据各影响因素贡献率大小,确定输电线路接地网腐蚀预测模型的输入量。
2)针对WPA存在的缺陷,对探狼游走位置和探狼、猛狼奔袭步长进行改进,仿真结果证明,IWPA能够减少迭代次数,加快算法速度。采用IWPA对LSSVM的惩罚参数和核函数参数进行优化,建立基于IWPA-LSSVM的输电线路接地网腐蚀预测模型。
3)采用IWPA-LSSVM预测模型对线路接地网腐蚀程度进行预测,并与其它模型进行比较,结果表明,IWPA-LSSVM预测模型的平均相对误差为3.47%,预测精度最高,均方根误差和全局最大相对误差分别为0.016 4和4.35%,均小于其他模型,外推预测的波动性更小,稳定性更好。
