随机激励作用下硬涂层薄板振动有限元分析及减振预估

孙 悦， 刘晓峰， 孙 伟

(东北大学 机械工程与自动化学院，沈阳 110819)

板类结构在航空航天领域得到了最为广泛的应用，例如航空发动机叶片、飞机蒙皮以及用于航天员存放物品的机柜等。这些板结构经常由于振动超标而影响整个结构的性能甚至发生振动疲劳破坏。涂敷硬涂层材料可以在一定程度上使结构件具有抗腐、隔热、抗磨等功能[1-2]。近些年来的研究发现[3]一些硬涂层材料还具有一定阻尼减振的作用，即使在高温高腐蚀的苛刻条件下依旧可以保持自身的阻尼能力。硬涂层减振技术是将由金属基、陶瓷基或者两者混合制成的涂层材料喷涂在结构的表面来实现减振目的，在板结构上得到了广泛应用[4-5]。

为了有效在板结构上实施硬涂层阻尼减振，需要创建相应的动力学分析模型用于对硬涂层减振效果进行可靠预估。上述板结构通常受随机载荷作用，因而需要研究随机激励载荷作用下，硬涂层板的振动特性建模与分析方法。

目前，在确定激励作用下硬涂层板或者类似板的结构已有大量研究，例如，Sun等[6]基于能量法，建立了硬涂层复合板结构的解析分析模型，求解了其固有特性及在基础激励作用下的振动响应。Filippi等[7]通过使用迭代有限元建模方法对硬涂层复合叶片在基础激励作用下的振动特性进行了分析。Li等[8]针对硬涂层悬臂薄板结构，研究其非线性振动机理并且采用有限元迭代法计算涂层板的振动特性。李然等[9]研究了涂层参数对整体叶盘振动特性的影响。从作者掌握的文献来看，关于硬涂层复合结构的建模与分析主要针对的还是涂层结构在确定激励作用下的振动特性分析。目前，还没有发现随机激励作用下涂层板结构振动分析实例。

研究者对随机激励作用下的板或者类板结构振动分析也开展了部分研究，例如20世纪60年代—20世纪70年代，Crandall等[10-12]对简支边界条件下矩形薄板、三角板、圆板等结构在点源随机激励作用下的振动响应进行了分析研究，并用实验进行了验证。Dogan[13]利用福克-普朗克方程研究了赫兹接触点的非线性随机接触振动，得到了每种情况下的稳态响应统计量。Chen等[14]基于虚拟激励法(pseudo excitation method，PEM)，求解了薄板结构在随机激励下的横向挠度、速度、加速度以及应力响应的解析功率谱密度(power spectral density，PSD)函数。

考虑到虚拟激励法具有计算精确且效率高的特点[15]，本文将采用虚拟激励法求解双面涂敷硬涂层薄板结构在随机载荷谱作用下的振动特性。首先，研发一种含双面涂层的4节点板单元，推导了相应的刚度及质量矩阵；接着将单元矩阵组集，在同时考虑材料及剩余等效黏性阻尼的基础上，确定了基础激励作用下悬臂涂层板结构的动力学有限元方程；再则，引入虚拟激励法，给出了求解涂层板结构在指定随机载荷谱下振动响应求解公式；最后，进行了实例研究，并进行了硬涂层参数对薄板振动特性的影响分析。

1 硬涂层板结构动力学有限元建模

这里研发了一种涂层板单元来模拟双面涂敷硬涂层的薄板结构的力学特性。所研究的悬臂板结构如图1所示，其中：Hc为硬涂层的厚度；Hs为基体厚度； 复合结构中性层和基体中性层重合， 基体到硬涂层中面的距离为Hsc。

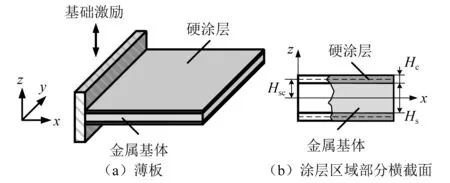
图1 双面涂敷硬涂层的薄板结构Fig.1 A double-covered hard-coating cantilever thin plate

1.1 涂层板单元的刚度及质量矩阵

这里采用等效单层理论进行涂层板结构的有限元建模，选用如图2所示的4节点板单元来模拟双面涂层结构。该单元每节点具有3个自由度，分别是两个转动自由度θx和θy，一个位移自由度w(挠度)、单元的长度为a，宽度为b。

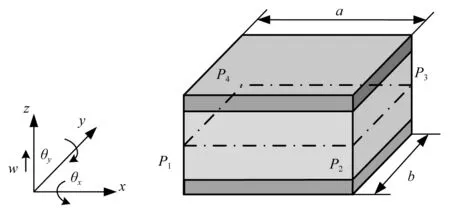
图2 涂层复合结构单元Fig.2 Quadrilateral plate element

单元内任意一个节点的位移δe为

δe=[w1θx1θy1…w4θx4θy4]T

(1)

进一步，单元内任一节点的形函数就可以写成

Ni=(1/8)[(XXi+1)(YYi+1)(2+XXi+YYi-X2-Y2),
(a/2)Xi(XXi+1)2(XXi-1)(YYi+1),
(b/2)Yi(XXi+1)(YYi+1)2(YYi-1)],
i=1,…,4

(2)

式中：Xi，Yi为节点的坐标；X，Y为[-1,1]的局部坐标。

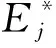
(3)

(4)

对于硬涂层复合板单元，其刚度矩阵可以表示为

(5)

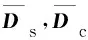
若基体的密度用ρs表示，硬涂层的密度用ρc表示，对于双面涂敷硬涂层板结构，其质量矩阵求解式为

Mc,e=∬NT(ρsHs+2ρcHc)Ndxdy

(6)

1.2 涂层板有限元方程建立

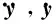
(7)

式中：Kc为涂层板结构包含涂层材料阻尼的复刚度矩阵；Mc为涂层板结构的质量矩阵；C2为由夹持边界及空气产生的剩余等效黏性阻尼矩阵；C1为涂层结构的材料阻尼矩阵；F(t)为激振力向量，其表达式为

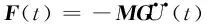
(8)

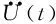
2 基于虚拟激励法的涂层板结构的随机振动响应分析

假如双面涂层薄板所受的激励是稳态随机激励，以下描述用虚拟激励法求解涂层结构随机振动响应的方法。参考式(7)涂层板结构新的运动方程可以表示为

(9)

按模态叠加法有

(10)

式中，Φ=[φ1φ2…φq]为前q前阶特征向量矩阵。

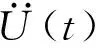
(11)

代入式(9)，则涂层板结构新的运动方程可以表示为

(12)

由于振型Φ关于C2，Mc，Kc具有正交性，所以式(12)也可以分解为n个单自由度方程，第j个可表示为

(13)

式中，ωj，ζj分别为第j阶对应的固有圆频率和系统中剩余等效黏性阻尼产生的模态阻尼比。

此单自由度简谐振动方程的稳态解表示为

(14)

式中，γj，Hj分别为第j阶对应的振型参与系数及频响函数。针对所描述的涂层板结构，有

(15)

式中，ηj为第j阶材料阻尼的模态损耗因子。提取涂层板前q阶的模态振型参与模态叠加后，式(12)的虚拟稳态解又可以写成

(16)

(17)

式中，上标H为取复共轭。在计算过程中，虚拟简谐激励因子eiωt与其复共轭e-iωt总是成对出现并最终相互抵消。这样式(16)的振动响应时域解就变为用功率谱密度描述的频域解。

3 分析实例

3.1 问题描述

本研究以火焰喷涂NiCrAl硬涂层的基体厚度为2 mm的悬臂薄板为例演示所描述的方法。所搭建的试验测试系统及试件，如图3所示。测试系统主要包括LMS 16通道便携式数据采集前端控制器、金盾EM-1000F电磁振动台、PCB 086C01型小力锤、B & K 4517轻质加速度传感器、LMS.Testlab笔记本工作站等。试验试件相关的材料参数，如表1所示。材料阻尼包含在黏弹性阻尼板的复刚度矩阵中，而剩余等效黏性阻尼需按照表2测得的阻尼处理前各阶模态阻尼比引入。通过锤击试验获得薄板的固有频率，利用电磁振动台采用非均匀一致载荷谱(如图4所示)对涂层板进行随机激励以获得加速度响应，激振方向垂直于薄板，锤击点及拾振点见图3。

图3 试验系统及试件Fig.3 Experimental system and test piece

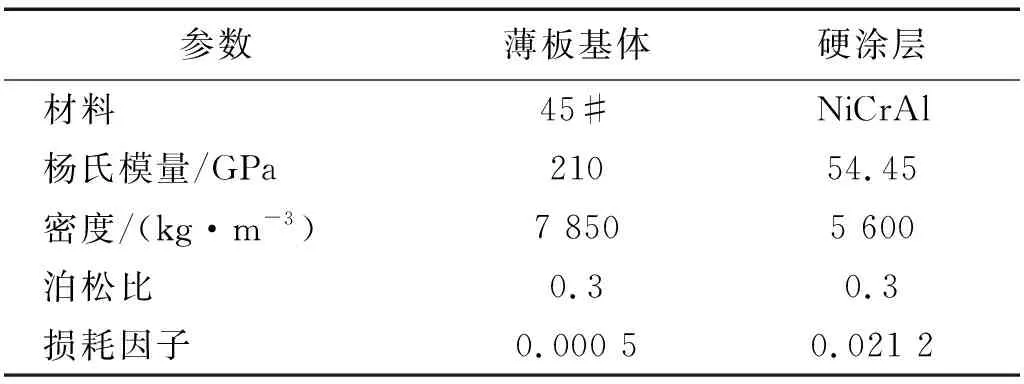
表1 涂层板材料参数Tab.1 Material parameters of the hard-coating plate

表2 涂层前薄板的模态阻尼比Tab.2 Modal damping ratios of the base plate without damping treatment

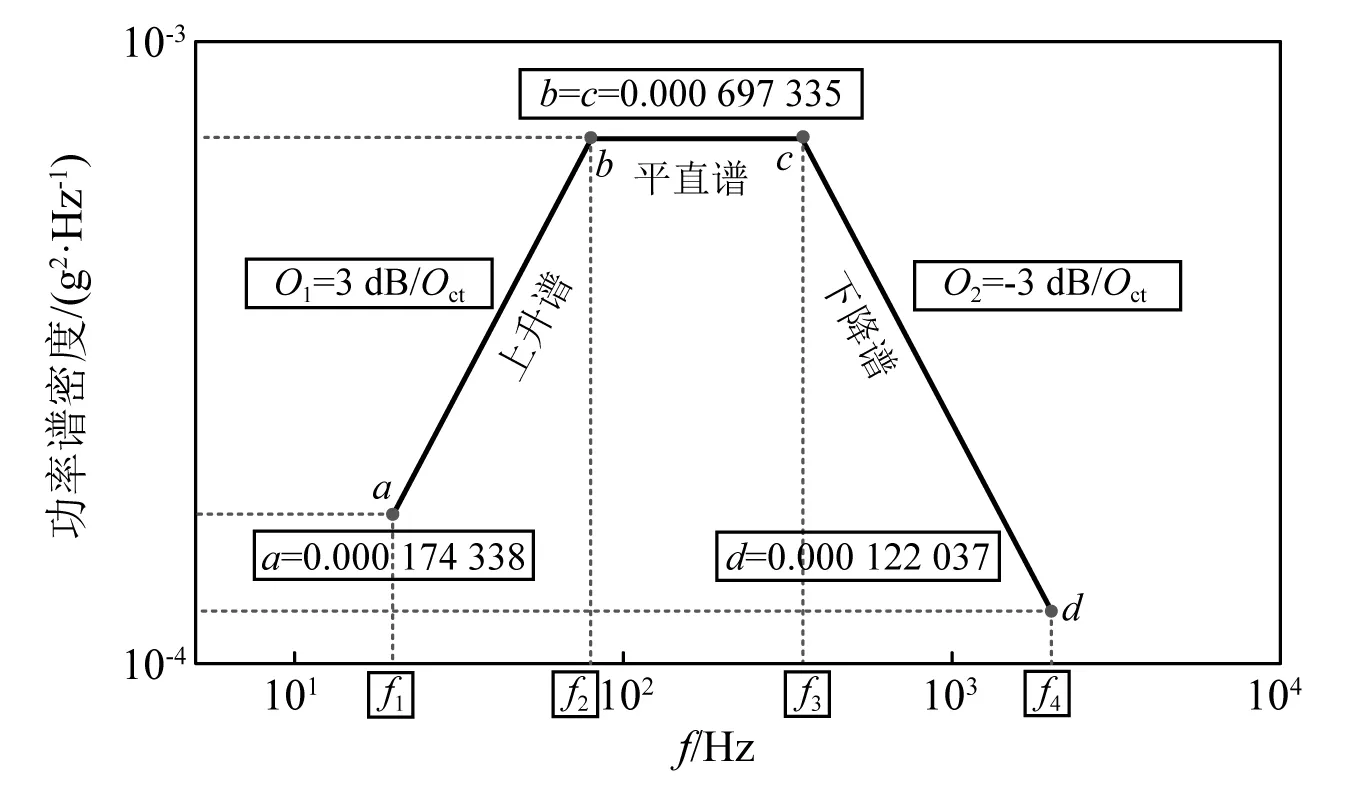
图4 非均匀一致载荷谱图Fig.4 Non-uniform and consistent load spectrum

以下将利用所研发有限元模型及求解随机振动响应的虚拟激励算法对涂层板结构进行分析，并利用该模型预估硬涂层在随机激励作用下的减振效果。

3.2 有限元模型验证

所创建的有限元模型如图5所示，涂层厚度为0.3 mm。为了验证有限元模型的正确性，采用锤击法对涂层前后薄板结构进行试验，其模态测试以及有限元分析后获得的固有频率数据，如表3所示。

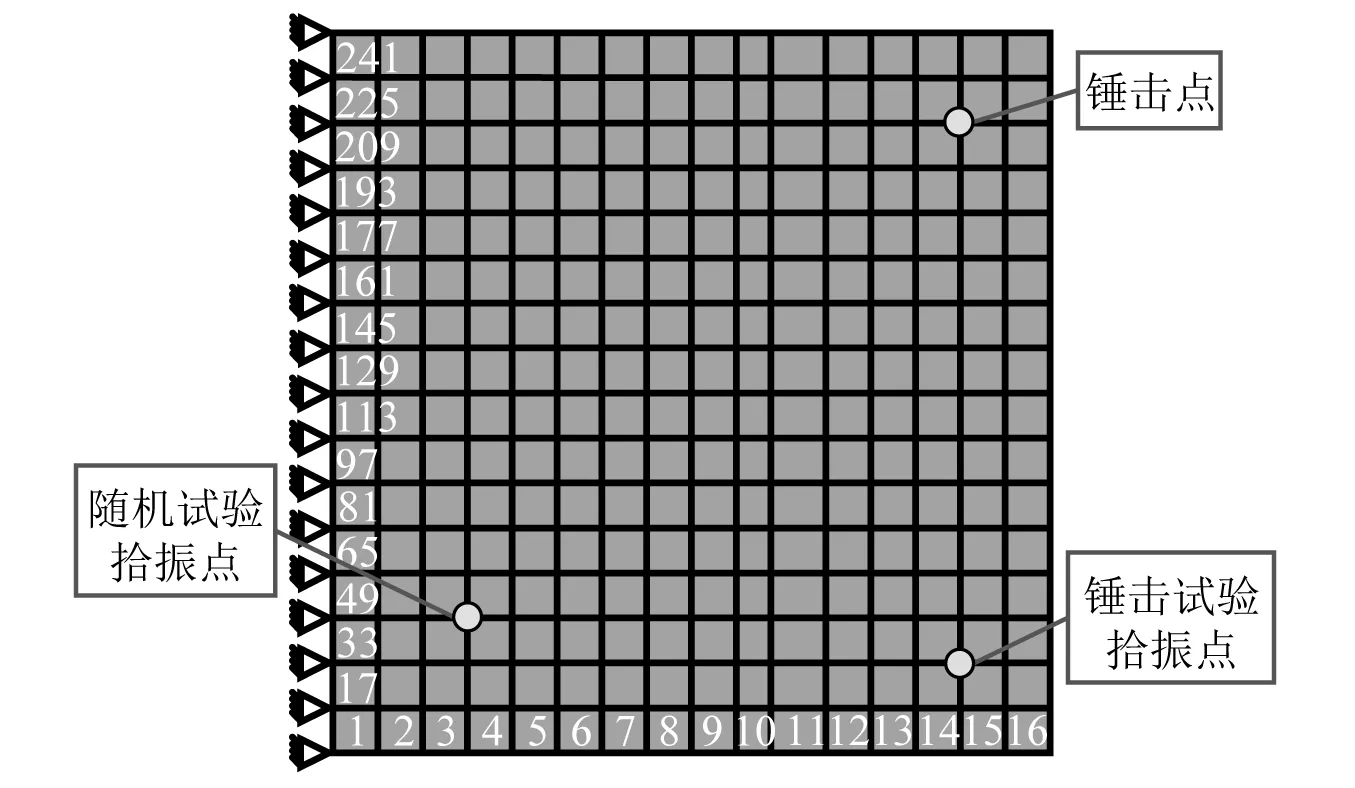
图5 涂层板有限元模型Fig.5 Hard-coating thin plate finite element model

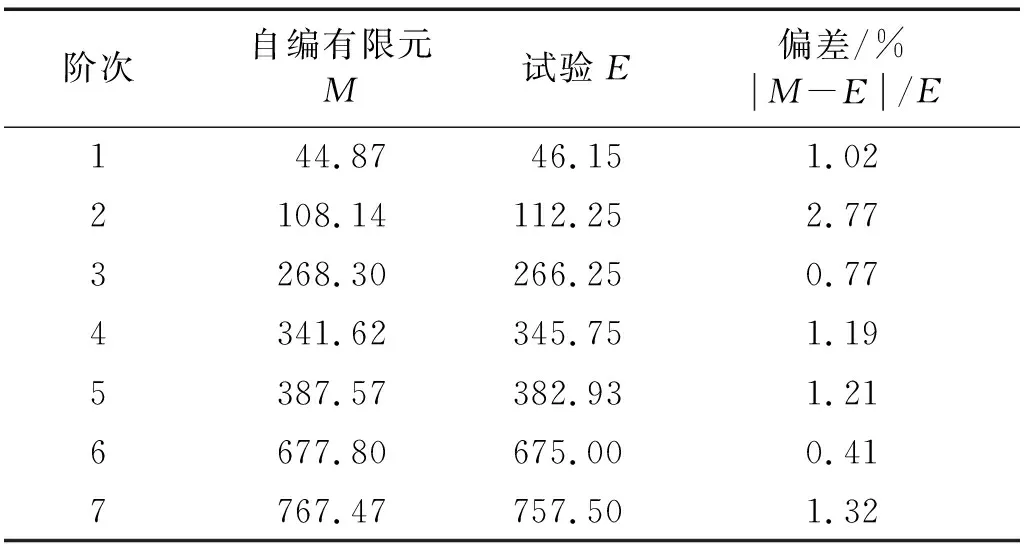
表3 自编有限元和试验获得的涂层后薄板的固有频率Tab.3 Natural frequencies of hard-coating thin plate obtained by MATLAB and experiment Hz

提取前7阶固有频率数据，通过对比试验与自编有限元方法计算分析结果可以得知，薄板涂层后固有频率最大偏差为2.77%。由此可见试验与自编有限元方法计算的固有频率结果具有很好的一致性，有限元模型可用于后续随机激励作用下的振动响应分析。

3.3 随机激励作用下涂层前后硬涂层板振动响应

针对试验应用的非均匀一致载荷谱激励，见图4。若采用分段函数的方式表达，其表达式为

(18)

通过式(18)计算可以得到输入载荷各个频率下对应的功率谱密度值。其中f=ω/(2π)，转换得到Sxx(ω)，进一步构造虚拟激励利用第2部分所给方法获得板结构的响应自功率谱密度。计算得到的响应结果与试验获得的响应结果如表4和图6所示。试验获得的涂层薄板响应加速度功率谱密度图中出现几个较小响应峰是由于试验环境噪音的影响。另外由于第6阶的振型表现为扭振，本文不做重点研究。

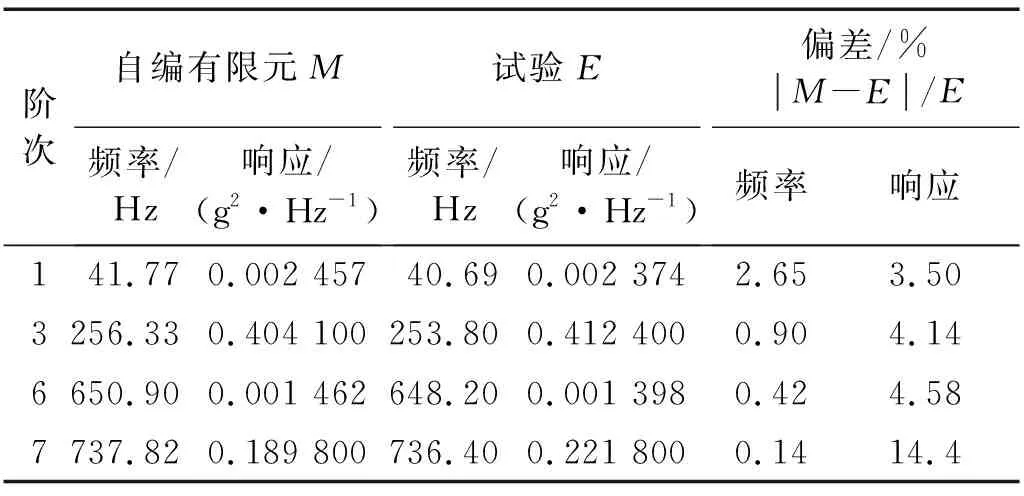
表4 理论计算和试验获得的涂层后薄板的随机振动加速度响应功率谱密度Tab.4 Random vibration acceleration response of hard-coating thin plate obtained by theoretical calculation and experiment

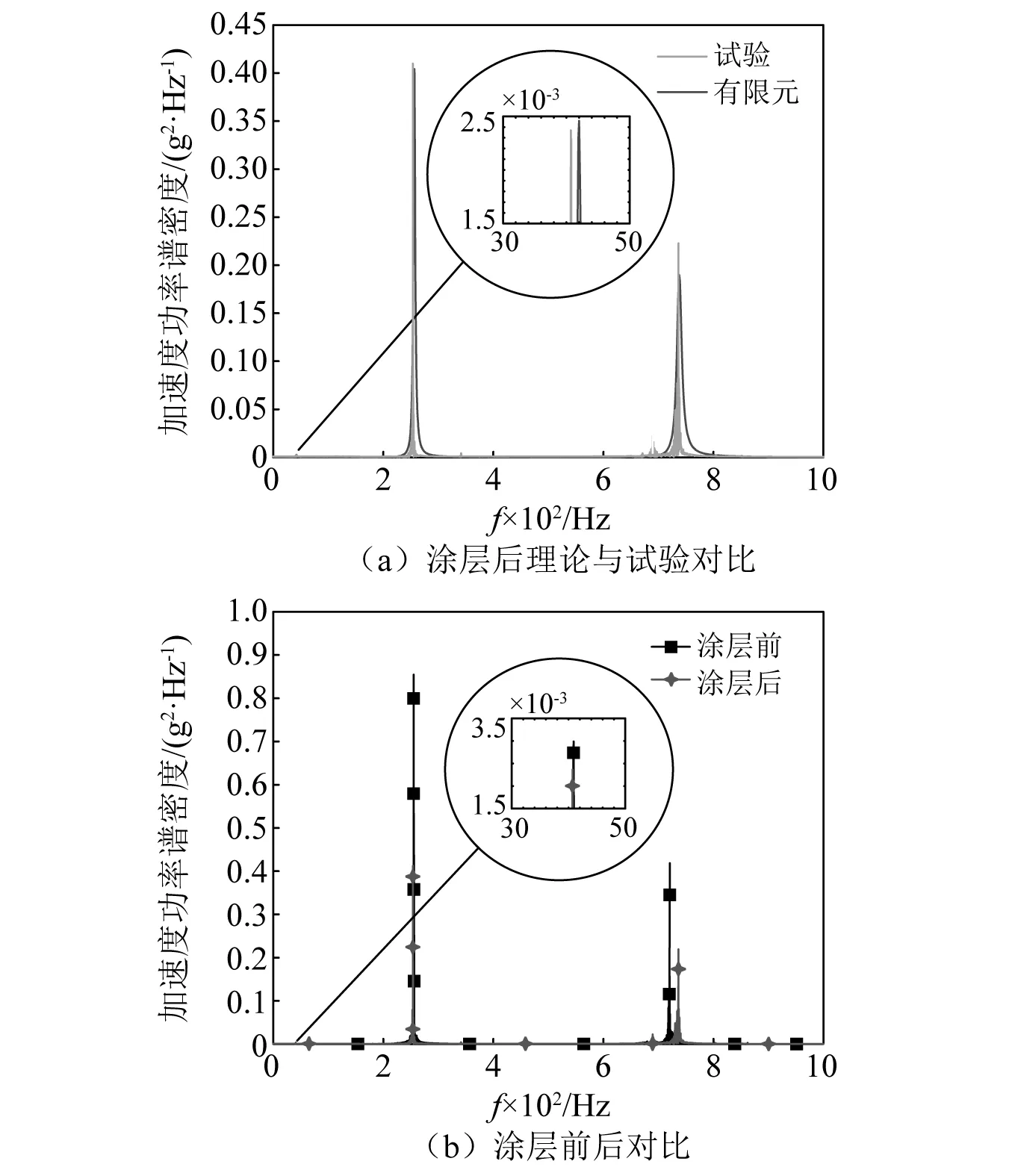
图6 涂层后薄板振动响应对比图Fig.6 The comparison of vibration response of thin plates after coating

由表4和图6可知，涂层板结构有限元方法获得的振动响应与试验结果具有很好的一致性。涂层后薄板的振动响应均比涂层前的光板有所降低，且幅度明显，由此可见，涂敷NiCrAl硬涂层材料可以实现一定程度上的减振效果。

4 涂层参数的影响

在实际工程应用中，涂层参数的改变会影响阻尼材料在复合结构中的减振能力。为确定最佳的涂层方式，研究在随机激励作用下涂层参数对涂层板结构的振动特性影响，涉及的涂层参数包括涂层厚度、涂层储能模量以及涂层损耗因子。

4.1 涂层厚度的影响

在研究随机激励作用下涂层厚度对涂层板振动特性影响时，对双面涂敷厚度分别为0.15 mm，0.20 mm，0.25 mm，0.30 mm的涂层薄板进行有限元建模。在求解出每块板固有频率的基础上，利用虚拟激励法求解出其在随机激励作用下，频率在0～1 000 Hz内的振动响应特性，求解结果如表5、表6和图7所示。

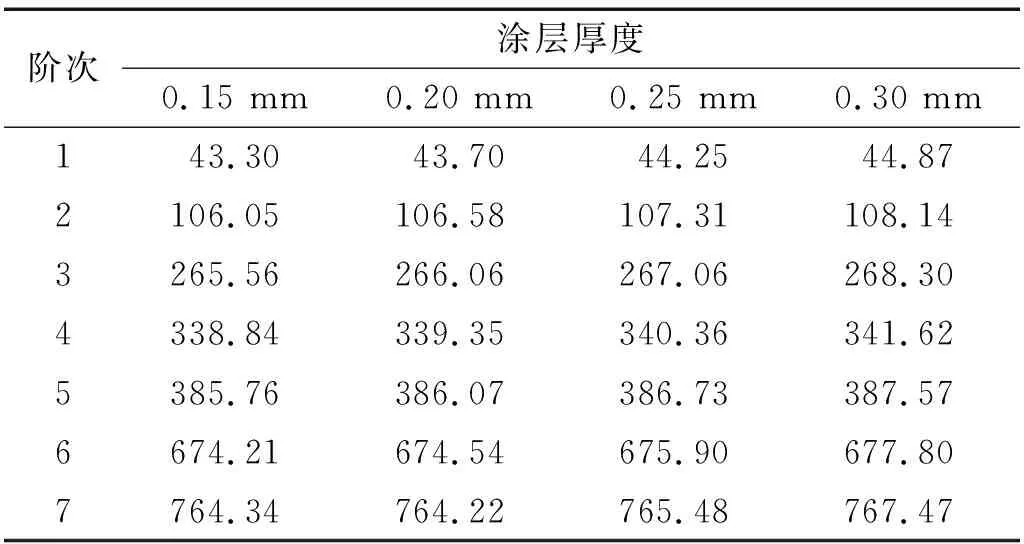
表5 具有不同涂层厚度的涂层板的固有频率Tab.5 The natural frequencies of hard-coating plates corresponding to different coating thicknesses Hz

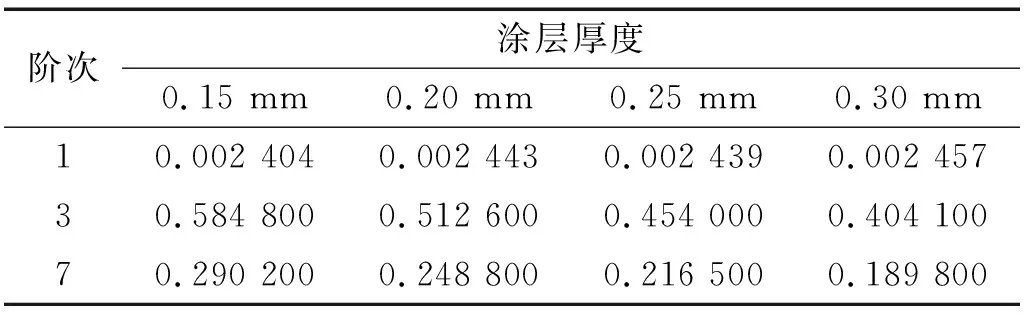
表6 具有不同涂层厚度的涂层板在随机激励作用下的振动响应Tab.6 The vibration response of hard-coating plates corresponding to different coating thicknesses under random excitation g2/Hz

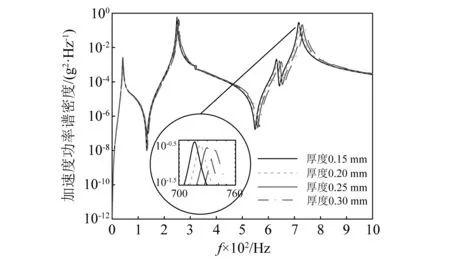
图7 具有不同涂层厚度的涂层板在随机激励作用下的频率-响应曲线Fig.7 Frequency-response curves of hard-coating plates corresponding to different coating thicknesses under random excitation

由计算结果可以看出，随着涂层厚度的增加，涂层板的固有频率会随之增大。在随机激励作用下，涂层板的振动响应加速度功率谱密度值会随着涂层厚度的增加而明显降低。这是因为涂层厚度的增加导致了涂层板结构各阶次的模态损耗因子增加，致使涂层板结构的阻尼增大，从而在一定程度上提高减振效果。

4.2 涂层储能模量的影响

涂层储能模量的数值分别为34 GPa，44 GPa，54.49 GPa，64 GPa，74 GPa时涂层薄板振动特性分析结果，如表7和表8所示。涂层储能模量的变化对涂层板结构振动响应特性的影响趋势，如图8所示。

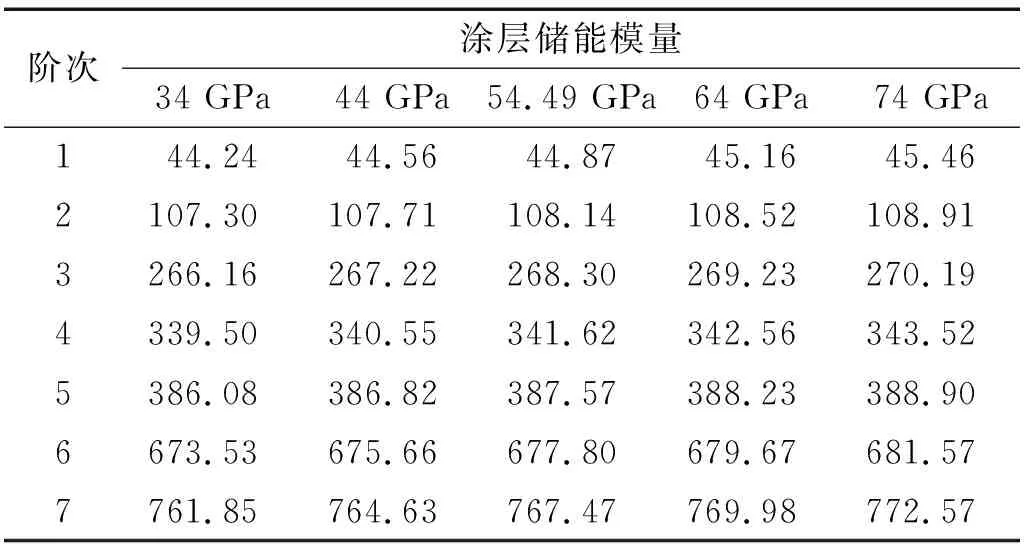
表7 具有不同涂层储能模量的涂层板的固有频率Tab.7 The natural frequencies of hard-coating plates corresponding to different coating storage modulus Hz

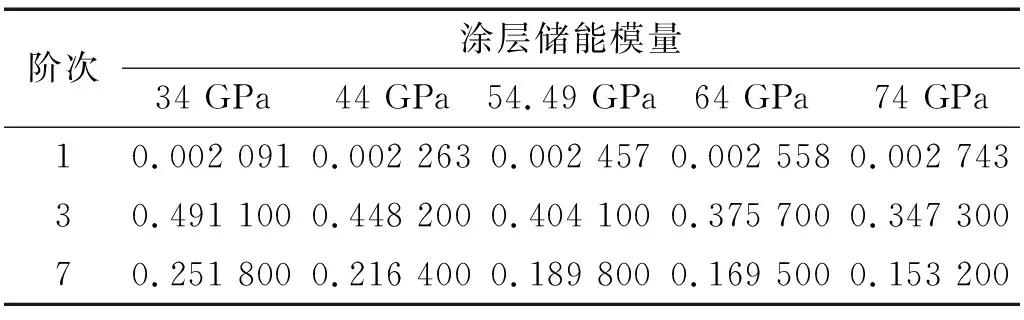
表8 具有不同涂层储能模量的涂层板在随机激励作用下的振动响应Tab.8 The vibration response of hard-coating plates corresponding to different coating storage modulus under random excitation g2/Hz

图8 具有不同涂层储能模量的涂层板在随机激励作用下的频率-响应曲线Fig.8 Frequency-response curves of hard-coating plates corresponding to different coating storage modulus under random excitation

由表7、表8和图8可知，随着涂层储能模量的增加，涂层板的各阶固有频率也随之提高。在随机载荷谱的作用下，随着涂层储能模量的增加，涂层板的振动响应加速度功率谱密度除第一阶有小幅度提高外(可忽略不计)其他两阶所对应响应峰值均随之降低。这是因为涂层的储能模量增加也会在一定程度上提高涂层板结构各阶次的模态损耗因子，致使结构的阻尼增大。

4.3 涂层损耗因子的影响

涂层损耗因子分别为0.012，0.017，0.021 2，0.027，0.032时涂层薄板振动特性分析结果，如表9和表10所示。出涂层损耗因子的变化对涂层板振动特性的影响趋势，如图9所示。

表9 具有不同涂层损耗因子的涂层板的固有频率Tab.9 The natural frequencies of hard-coating plates corresponding to different coating loss factors Hz

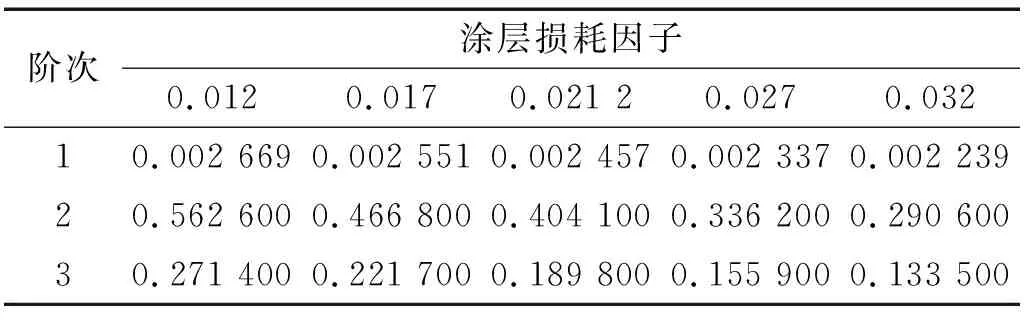
表10 具有不同涂层损耗因子的涂层板在随机激励作用下的振动响应Tab.10 The vibration response of hard-coating plates corresponding to different coating loss factors under random excitation g2/Hz

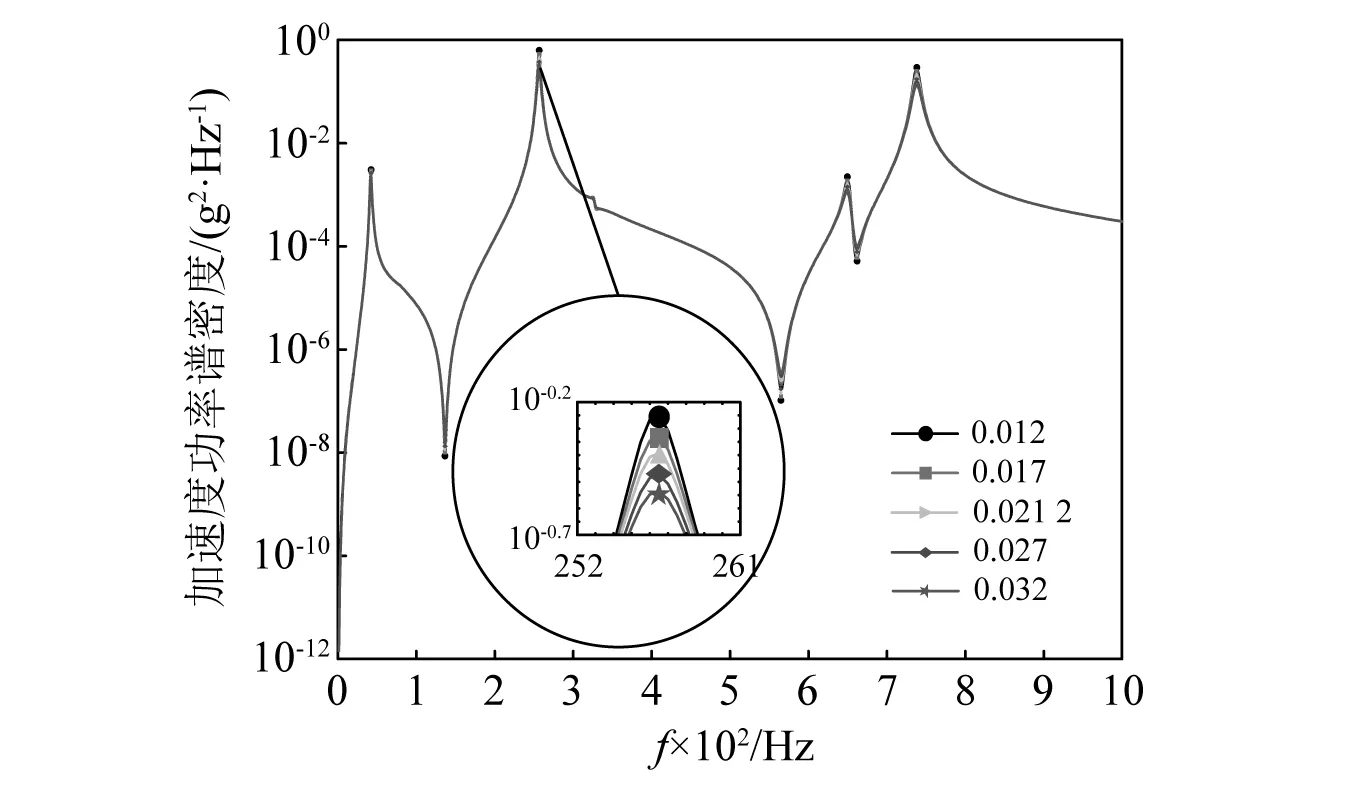
图9 具有不同涂层损耗因子的涂层板在随机激励作用下的频率-响应曲线Fig.9 Frequency-response curves of hard-coating plates corresponding to different coating loss factors under random excitation

由表9、表10和图9可知，涂层的损耗因子的改变对涂层板的固有频率没有影响，这是因为涂层损耗因子的改变，对涂层板结构的刚度与质量矩阵没有影响。但在随机激励的作用下随着涂层损耗因子的增大，涂层板结构的阻尼增大，涂层板的振动响应加速度功率谱密度值会随之减小。

5 结 论

本文针对双面涂敷硬涂层的薄板结构建立了有限元模型，基于虚拟激励法对在随机激励作用下的涂层板的振动响应特性进行了分析。得出相关结论如下：

(1) 利用等效单层法所研发的4节点双面涂敷硬涂层的薄板单元可有效模拟复合板结构的振动特性，通过固有频率计算表明所考虑各阶次计算结果与试验的最大偏差为2.77%。在明确将随机载荷谱转化为简谐激励方法的基础上，虚拟激励法可有效求解稳态随机激励作用下硬涂层悬臂板的振动响应，结果表明计算获得的各阶次振动响应功率谱密度与试验最大偏差为14.4%。

(2) 悬臂薄板双面涂敷硬涂层后，其固有频率以及振动响应功率谱密度都发生了一定的变化，计算及试验结果均表明涂敷硬涂层后可在一定程度上降低板结构的振动响应峰值，起到一定的减振作用。进一步，通过分析硬涂层厚度、储能模量、损耗因子等涂层参数对涂层板结构振动特性的影响表明：在合理范围内适当增加涂层的厚度、储能模量以及损耗因子均能在一定程度上提高减振效果。