负刚度时滞反馈控制动力吸振器的反共振优化

2022-02-26赵艳影

振动与冲击 2022年4期

代晗，赵艳影

(南昌航空大学飞行器工程学院，南昌 330063)

传统的线性可调动力吸振器是一种放置在主系统之上并吸收主系统能量的吸振装置。第一个无阻尼吸振器是由Frahm[1]提出的,该吸振器利用目标频率处产生反共振达到完全抑制主系统振幅的目的,但是有效的频率调控范围仅在反共振点附近较窄的频带区间。Den Hartog等[2-3]的研究发现：在吸振器中加入阻尼,不仅克服了无阻尼吸振器频带窄的缺点,同时能有效抑制主系统的振幅；主系统的频响曲线始终通过两个固定点,并且不受吸振器阻尼值的影响,这一发现为结构参数优化提供了固定点理论的支撑。Asami等[4-5]采用固定点理论原理,在保证两个共振峰幅值相等且最小的前提下,对有阻尼吸振器进行结构参数优化,得到吸振器最优结构参数的精确解。文献[6]利用正负刚度并联相消原理,设计了具有负刚度结构的隔振系统,利用能量准则推导了弹性系统静态稳定性的刚度准则,证明了负刚度系统具有固有频率低、承载能力大、隔振效果好的优点。

彭海波等[7]对含有负刚度元件的动力吸振器系统进行参数优化设计,用固定点理论得到了负刚度吸振器的最优频率比和最优阻尼比,研究表明负刚度动力吸振器比传统动力吸振器减振能力更强、减振频带更宽。王孝然等[8]对含有负刚度弹簧元件的三要素型动力吸振器进行参数优化设计,利用固定点理论将三个固定点调节到同一幅值,得到最优负刚度比,该减振器具有很好的减振性能。郝岩等[9]对含负刚度器件的Maxwell模型动力吸振器参数进行优化,同样利用固定点理论将三个固定点调节到同一幅值,得到最优负刚度比,该减振器能大幅度降低共振区振幅,并且具有较宽的减振频带。邢昭阳等[10]将杠杆放大机构与负刚度结构联合使用,能更大幅度降低共振振幅、拓宽减振频带,同时降低系统的谐振频率。陈杰等[11]将含有惯容器和负刚度的动力吸振器用于抑制梁的横向振动,负刚度能够很好抑制梁的振动,而惯容器能进一步起到抑制作用。

然而，利用负刚度来进行吸振和隔振，反共振点的幅值仍然很大。Flannelly[12]首先提出利用动力反共振隔振器,并通过试验证明了其在低频和单频工况下隔振效果很好。文献[13-14]把动力反共振隔振器应用到直升机旋翼和传动装置,动力反共振隔振器装置的设计质量仅为直升机总质量的1.3%。李园园等[15]用灵敏度分析和响应面方法,对动力反共振隔振器的隔振效率和配重动能进行了优化,隔振效率有了极大的提高,并指出隔振效率与外激励大小无关。被动式动力反共振隔振器的有效减振频带宽度受限。周为民等[16]提出了一种主动反共振隔振装置,该装置由主动控制发生器和反共振隔振装置组成,在改善了被动控制的稳定性和传递特性的同时,又拓宽了减振频带,对随机激励和简谐激励两种激励并存的场合效果更好。范德礼等[17]提出了一种反共振频率可调的液压式动力反共振隔振器,反共振频率是通过调节空气弹簧的刚度来实现,并用遗传算法对隔振器的结构参数进行优化设计,得到了更宽的隔振频带。沈安澜等[18]提出了一种新型聚焦反共振式主减隔振装置,其结果表明,这种型式的隔振装置对垂向、航向和侧向三向激励很有效,隔振效率均达到了80%。

被动式的线性吸振和线性隔振控制的频带有限,对变频和宽频外激励的振动控制效果差。Olgac等[19]首先提出采用时滞动力吸振器控制系统振动,时滞减振是一种主动减振技术,能实时追踪外激励频率在反共振点处完全抑制主系统的振动。Zhao等[20]研究了时滞减振在非线性系统中的应用,非线性时滞动力吸振器比线性时滞动力吸振器具有更宽的减振频带和更大范围的稳定性。Meng等[21]研究了时滞耦合非线性振动系统的等峰优化问题,利用增量谐波法和优化方法对结构参数进行优化,有效地解决了外激励幅值较大的情况下,非线性振动系统等峰优化问题。本文通过在接地负刚度系统中耦合进时滞反馈控制得到一种含有负刚度时滞反馈控制动力吸振器模型。该模型首先用固定点理论得到不含时滞反馈控制的最优负刚度系统结构参数;接着在保证系统稳定的前提下,利用反共振峰最小准则,通过调节时滞反馈控制参数和进一步调节系统结构参数,得到一组能使负刚度时滞反馈控制系统具有较宽的减振频带和较对称的减振频带的最优系统参数,同时也保证了在该减振频带内系统的振动幅值大大降低，最主要的创新是在反共振频率下的幅值满足所提出的反共振峰值最小准则。

1 力学模型及振动微分方程

1.1 时滞耦合负刚度吸振器系统

为了进一步拓宽负刚度系统的减振频带,并提高减振性能,考虑在彭海波等所研究的接地负刚度型动力吸振器中加入位移时滞反馈控制,同时考虑主系统的阻尼,接地负刚度时滞反馈控制的吸振系统，如图1所示。图1中：k为变刚度的接地负刚度元件的刚度数；m1,m2,c1,c2,k1和k2分别为主系统和吸振器的质量、阻尼和刚数；g1和τ分别为时滞反馈增益系数和时滞量；x1和x2分别为主系统和吸振器的位移；F0为外激励力的幅值；ω为外激励频率。

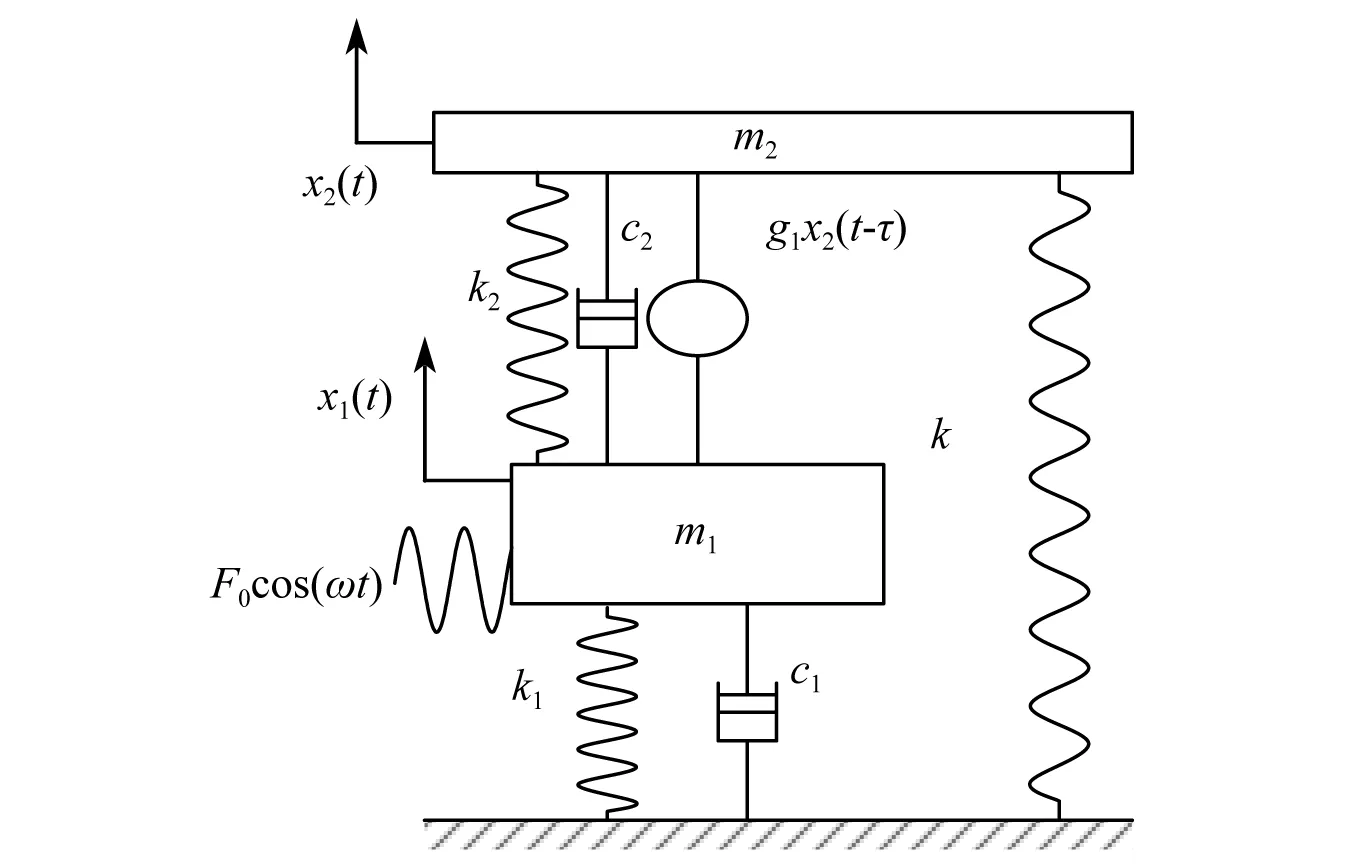
图1 时滞耦合负刚度吸振器系统的力学模型Fig.1 Mechanical model of delay-coupled negative stiffness system

由牛顿第二定律得到上述系统的运动微分方程

(1)

为了使方程更具通用性,对式(1)进行无量纲处理,为此引入如下相关参数及无量纲量

(2)

(3)

设式(3)的解为

(4)

将式(4)代入式(3)可解得

(5)

Δ(Ω)=[2jΩ(pμξ2+ξ1)+μp2-Ω2+1]·
[p2ge-jΩτ+2jpξ2Ω+(α+1)p2-Ω2]-
(p2+2jpξ2Ω)(μp2+2jpμξ2Ω+μp2ge-jΩτ]

(6)

引入变量A1和A2分别代表主系统和吸振器的振幅如式(7)所示

(7)

1.2 接地负刚度吸振器系统

若令主系统的阻尼系数ξ1=0,时滞反馈控制增益系数g=0,接地负刚度位移时滞反馈控制的吸振器就退化为彭海波等所研究的接地负刚度型动力吸振器,无量纲运动微分方程式(3)退化为如式(8)所示的被动吸振器系统运动微分方程

(8)

Asami等、Nishihara等和彭海波等是通过固定点理论对两个共振峰进行优化来寻找最优结构参数sp={μ,ξ2,α,p},满足条件

min‖A1(sp,Ω)‖∞=
min{max[A1(sp,Ω1),A1(sp,Ω2)]}→
A1(sp,Ω1)=A1(sp,Ω2)

(9)

式中：A1(sp,Ω)为主系统频率响应；Ω1和Ω2分别为一阶和二阶共振频率。彭海波等通过设计下列结构参数优化两个共振点的幅值

(10)

对接地负刚度动力吸振器系统, 彭海波等通过优化使两个固定点处于相似高度和峰值位置,得到如图2所示的幅频响应曲线。

图2 最优结构参数下的幅频响应曲线Fig.2 Amplitude-frequency response curve for optimal structural parameters

从图2中可以看出,在被动负刚度振动系统中根据固定点理论进行等峰设计和参数优化后,主系统的两个共振峰及反共振点的幅值仍然很大,本文采用时滞反馈控制进一步控制主系统的振幅。

2 力学模型及振动微分方程

2.1 时滞耦合负刚度吸振器系统

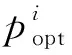
(11)

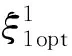
(12)

{0.1,0.501 7,0.356 2,1.408 5,-0.705 9}

(13)

在式(13)最优结构参数前提下,为了得到控制增益g和时滞τ的稳定区间,式(3)的特征方程为

(14)

由于时滞项的存在,特征方程式(14)是含有指数项e-λτ的超越方程,系统是无限维的,含有无穷多个特征根。针对这样的问题,本文考虑用CTCR(cluster treatment of characteristic roots)法[22]进行分析,具体步骤如下:

步骤1定义(kernel hypercurves，KH)——当固定系统结构参数在某一值,(τ,g)的二维平面内一点引起一个实部为0的特征值λ=jΩc,Ωc∈R+,且0≤Ωcτ≤2π,0≤g≤2,所有在二维平面区间内的这样的点组成曲线,称其为KH。

步骤2定义(offspring hypercurves，OH)——上述定义的KH通过以下非线性转换式得到OH

(15)

步骤3定义根的变化趋势(root tendency，RT)

(16)

当τi∈(τi-ε,τi+ε),0<ε≪1,i=1,2,3,…时,当TR=1表示时滞从左侧穿过临界时滞τi时,不稳定根的个数增加两个; 当TR=-1表示时滞从右侧穿过临界时滞τi时,不稳定根的个数减少两个;在时滞其他区间不稳定根的个数不变。

步骤4对指数项进行替换

e-jΩcτ=cosvc-jsinvc,vc=Ωcτ

(17)

其中正弦函数sin和余弦函数cos是用正切函数tan的半角公式进行如式(18)的转换

(18)

下面依据CTCR理论,对系统稳定性进行分析。

由式(17)和式(18),特征方程式(14)可以写成关于Ωc的多项式函数

(19)

式中，ck为关于g,z1的函数,是Ωc的系数。

对式(19)进行实虚部分离,整理得到

(20)

(21)

式中，Qk,Pk为关于g,z1的函数,也是Ωc的系数,具体如下

Q2=-1-p2(1+g+α+u)-4pξ1ξ2-

Q1=4gp2z1ξ1,

P4=0,P2=2gp2z1,

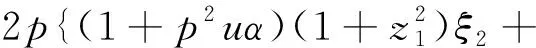
P0=-2gp2z1。

要从式(20)和式(21)中解出Ωc,需应用Dixon等[23-24]结式和判别式得到其充分必要条件。Dixon结式和Sylvester[25], Macaulay[26], Sparse[27]结式一样,都是求解多项式非平凡解的充分必要条件,但是Dixon结式比其他结式精确度更高。

依据Dixon结式,令

q1(Ωc)≡Re[q(Ωc,g,z1)]

(22)

q2(Ωc)≡Im[q(Ωc,g,z1)]

(23)

(24)

式中：q1(φ)和q2(φ)为虚变量φ替换Ωc；q1(Ωc)和q2(Ωc)的表达式为

{-1-p2(1+g+α+u)-4pξ1ξ2-

得到的式(24)是关于Ωc和φ对称的deg-1次多项式,也称是关于q1(Ωc)和q2(Ωc)的Dixon多项式。由于式(24)是对称性的多项式,调换因变量位置式(24)的表达式不改变,即δ(Ωc,φ)=δ(φ,Ωc)。

上述的deg=max{deg[q1(Ωc)],deg[q2(Ωc)]}其中的deg[q1(Ωc)]和deg[q2(Ωc)]是关于Ωc的最高阶数,q1(Ωc)和q2(Ωc)的每个共同零点同样也是δ(Ωc,φ)对所有φ值的零点。因此,我们得出,在共同的零点情况下,δ(Ωc,φ)中φi(i=0,1,2,…,deg-1)的系数等于0，用矩阵的形式表示

(25)

式中, 系数矩阵D(g,z1)∈Rd称作Dixon矩阵,d=deg×deg。

求解式(25)的一个非平凡解,要求D(g,z1)是奇异矩阵,即

det[D(g,z1)]=0

(26)

式(26)是关于g,z1的多项式,进一步转化得到形式上关于z1的多项式

(27)

式中：l=0,1,2,…,d；系数Rl(g)较复杂,未列出。

为了得到g和τ的稳定区间,按以下步骤进行求解:

步骤1固定参数g,求解式(27)的根,选取实数的根代入式(18)；

步骤2从式(18)求得vc后代入式(17),得到e-jΩcτ,将之代入式(14),得到所有的特征根；

步骤3从所有特征根中选取纯虚根,标记为Ωc,将Ωc和步骤2求得的vc代入式(17),求得τi,i=1,2,3,…；

步骤4g线性递增,重复以上步骤,直到g=2,得到r1={(g,τ)|Re[CE(p,g,τ)]<0}∩r0，其中，参数p={μ,ξ1,ξ2,p,α}={0.1,0.501 7,0.356 2,1.408 5,-2～0}。

2.2 反共振点幅值最小准则

下面分析采用时滞反馈主动控制来研究反共振点的优化问题,系统的运动微分方程即为式(3)。

利用时滞反馈控制反共振点的幅值及反共振频率的位置,需要设计反共振点振幅最小准则,首先需要得到反共振点的频率和幅值,利用函数最小值原理,得到主系统振幅极小值条件为

(28)

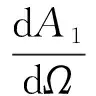
本文是一个两自由度线性系统,主系统振幅极小值条件也是求得反共振点的条件。首先从式(28)求得反共振点的频率,将之代入式(7)得到反共振点的幅值。对于给定的结构参数p,通过调节反馈增益系数g和时滞系数τ,将反共振点的幅值控制在给定的足够小的幅值范围内,即min‖A1(p,Ωa,g,τ)‖<0.01,我们就得到反共振点最小的优化准则满足

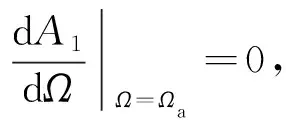
(29)

式中，A1(p,Ωa,g,τ)为反共振点的幅值,Ωa为反共振点频率,设定r2为满足反共振点幅值最小准则且稳定的g和τ的区间,如式(30)所示

r2={(g,τ)|min‖A1(p,Ωa,g,τ)‖<0.01}∩r1

(30)

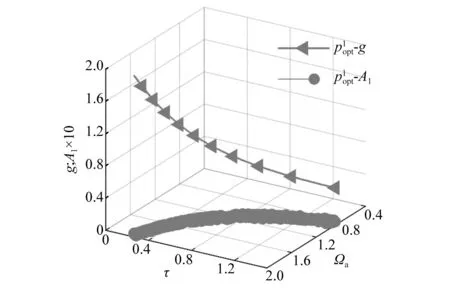
图3 时滞主动控制反共振点幅频响应曲线Fig.3 Amplitude-frequency response curve at anti-resonance point in time delayed active control

从图3观察到满足反共振点频率振幅在小于0.01范围内,在Ωa∈(0.9,2.0)内存在反馈增益系数g和时滞τ的一段调节区间,然而时滞反馈控制在的低频区域失效。一般情况下,工程当中希望主动控制的频率调节范围能够对称地分布在主共振点的两侧,显然图3中的主动控制范围主要控制在高频区域,因此需要采用对结构参数p进行优化设计的同时联合时滞反馈主动控制,从而达到最优控制效果，即同时满足反共振点的幅值、频宽、频带对称性的要求。

首先设定结构参数初始值p0为

p0={μ,ξ1,ξ2,p,α0}=
{0.1,0.501 7,0.356 2,1.408 5,0}

(31)

然后把结构参数p0和p划分为N等分,Δp=(p0-p)/N,N越大,Δp越小精度越高,此处取N=100,其中的结构参数μ,ξ1,ξ2和p固定不变,α的取值为p0～p;第h+1步的结构参数ph+1=ph+Δp,ph为第h步的结构参数,h=0,1,2,…,N。

最后,把结构参数ph+1代入式(29)和式(30)，求得满足反共振点幅值最小准则的反馈增益系数g和时滞τ,循环流程图如图4所示。

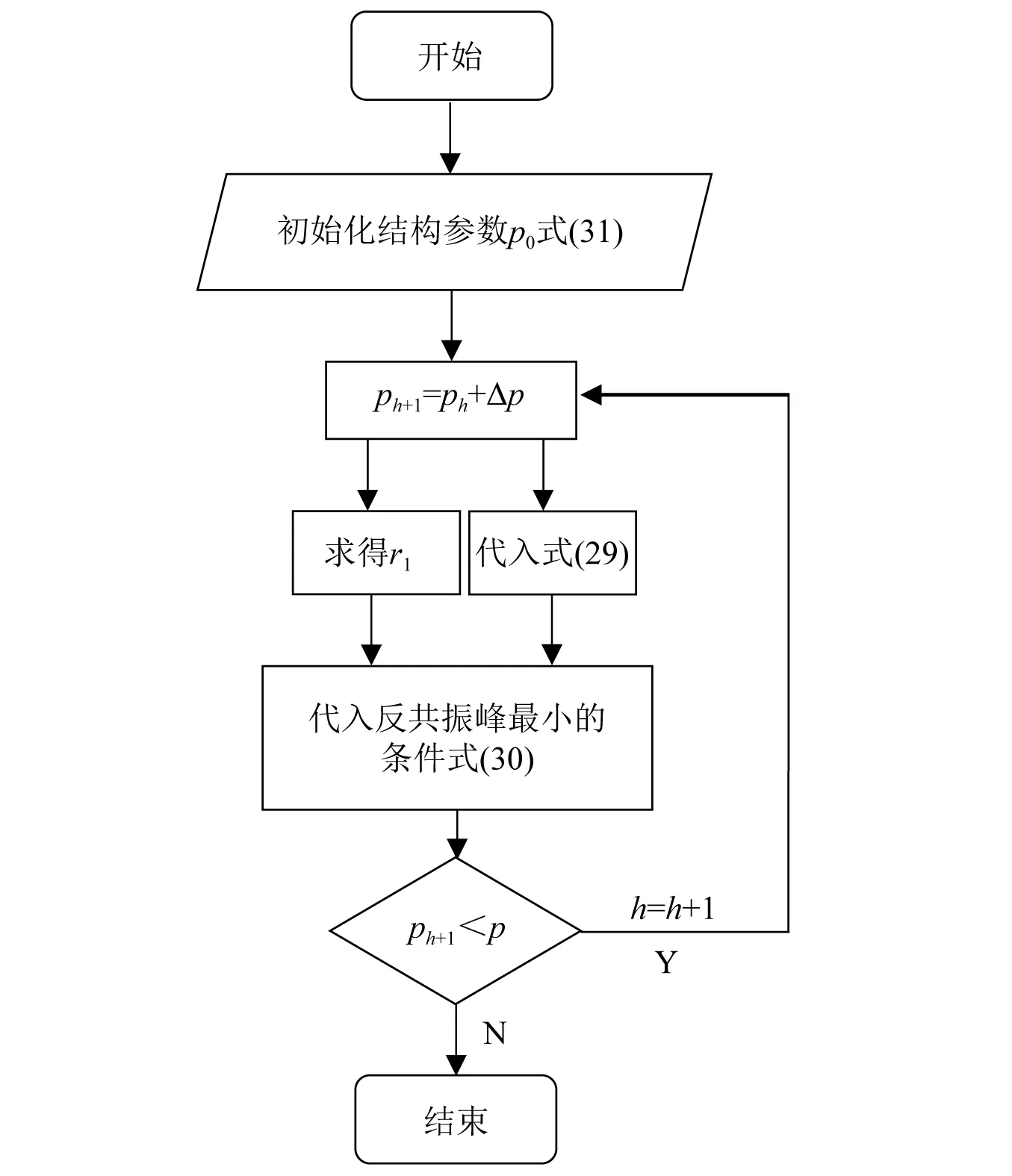
图4 反共振点计算流程图Fig.4 The flow chart of anti-resonance point

从图5(a)和图5(b)中可以看出,随着负刚度系数α的绝对值不断增大,反馈增益g和时滞τ可调节的稳定区间不断变小。

图5 不同α下g和τ稳定区间Fig.5 The stable intervals of g and τ under different α

图6 不同α下g和τ可控反共振频率范围和最小反共振频率幅值Fig.6 The controllable anti-resonance frequency ranges and the minimum anti-resonance frequency amplitudes of g and τ under different α

{0.1,0.501 7,0.356 2,1.408 5,-1.090 9}

(32)

然而，此时选定的最优结构参数对于我们所要求的可调控的反共振点频带对称性的要求还相差甚远,下一步通过优化主系统阻尼系数并结合时滞主动控制来达到可调控的反共振点频带对称性的目的。

目前优化后的系统结构参数以及下一步需要优化的主系统阻尼系数变化范围，如表1所示。

依据表1的结构参数值,再次应用计算反共振点幅值最小的流程图4,得到满足反共振点幅值最小准则的增益系数g和时滞τ的稳定区间,如图7所示。从图7(a)和图7(b)中可以看出,随着主系统阻尼系数ξ1的不断增大,反馈增益系数g和时滞τ可调的稳定区间先增大后减小。

表1 结构参数p0和pTab.1 The structural parameters of p0 and p

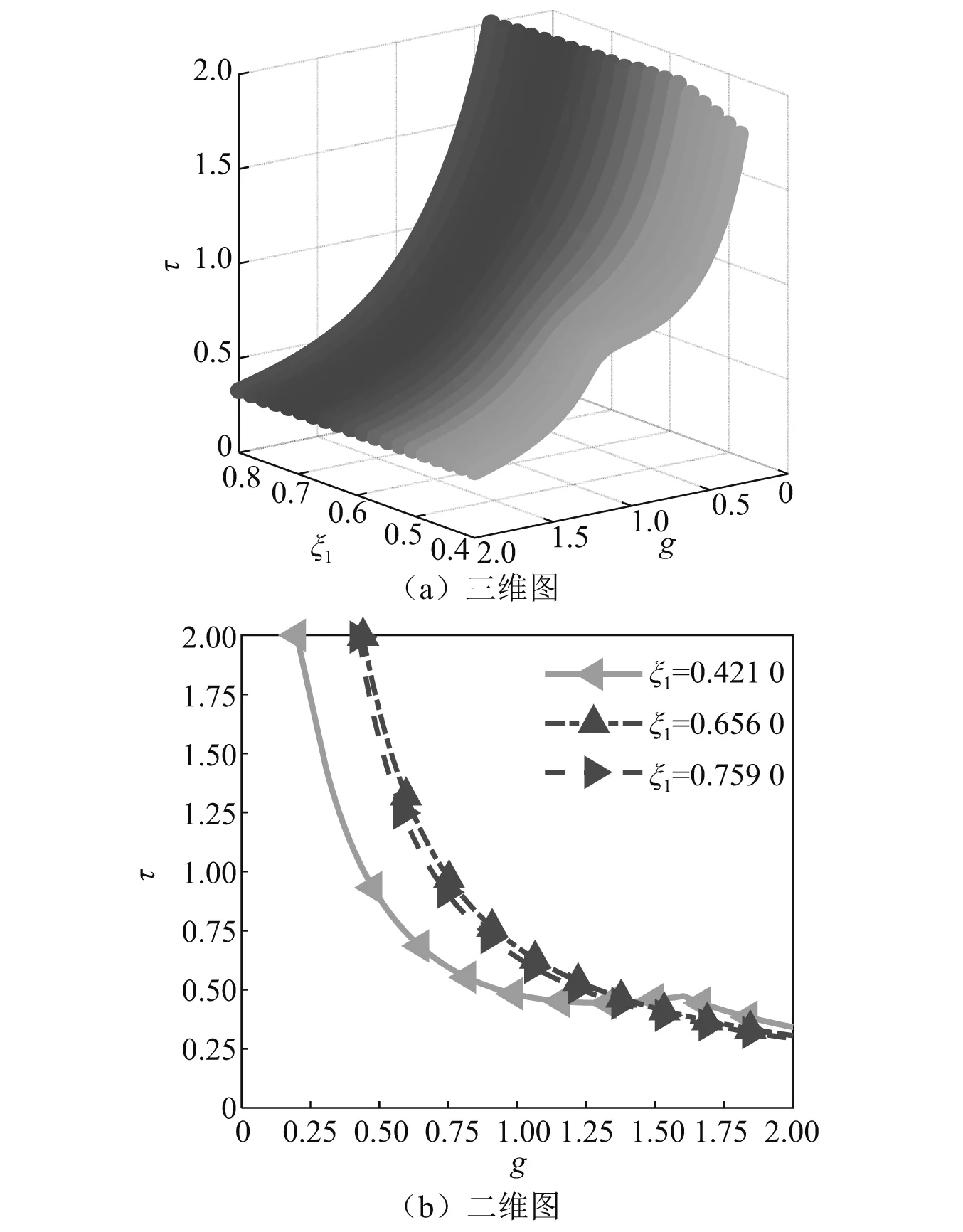
图7 不同ξ1下g和τ稳定区间Fig.7 The stable intervals of g and τ under different ξ1

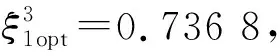
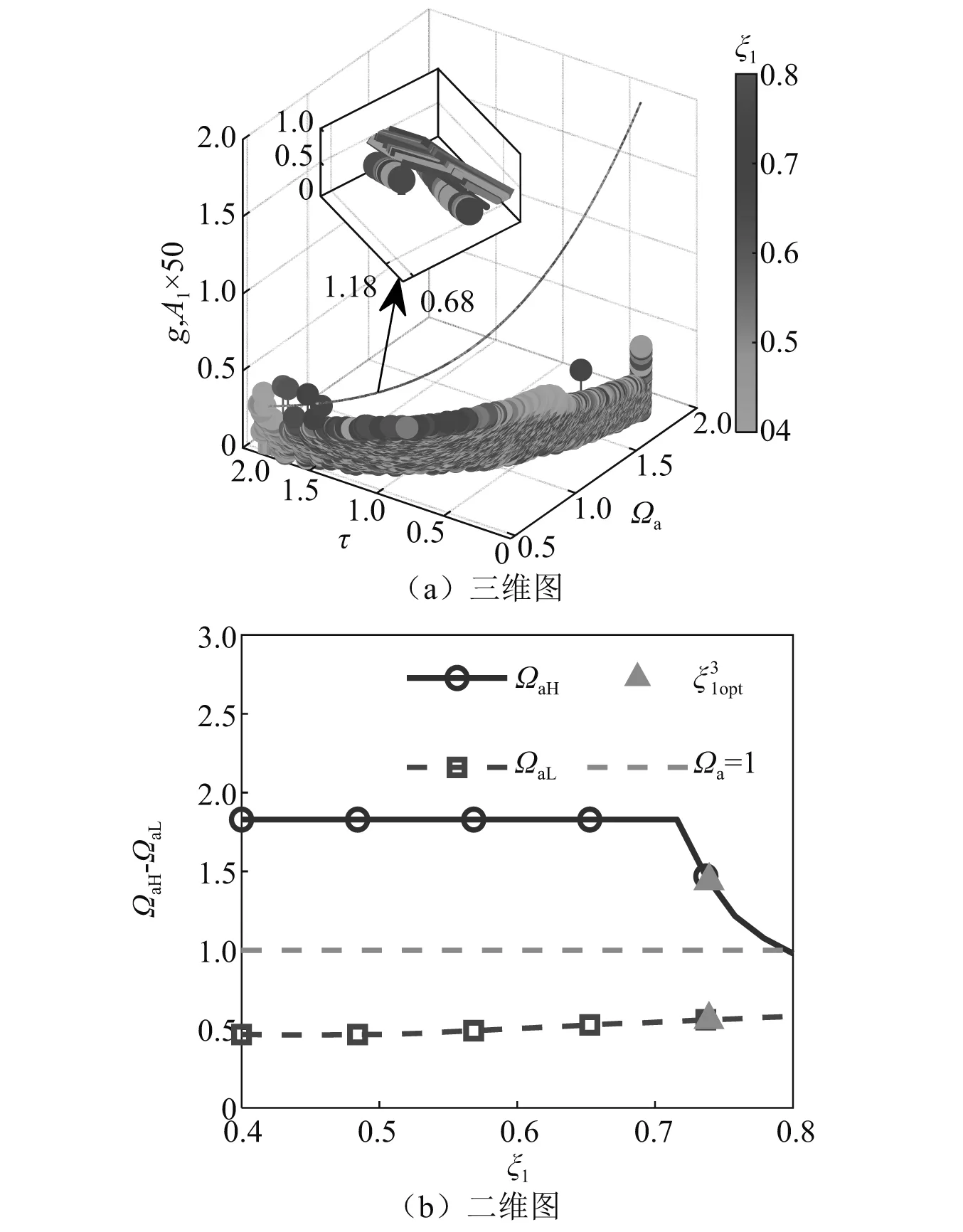
图8 不同ξ1下g和τ可控反共振频率范围和最小反共振频率幅值Fig.8 The controllable anti-resonance frequency ranges and the minimum anti-resonance frequency amplitudes of g and τ under different ξ1

{0.1,0.736 8,0.356 2,1.408 5,-1.090 9}

(33)

3 验证与分析

第2章讨论了一种反共振点频率范围及最小反共振点幅值的优化方法,得到各步骤的最优结构参数如表2所示。本章应用如图4所示的循环流程图,得到上述三步中每一步结构参数的优化结果，如图9所示。

图9 g和τ的反共振频率的范围和对应频率的最小振幅Fig.9 The ranges of anti-resonance frequency and the minimum amplitudes of corresponding frequency controlled by g and τ

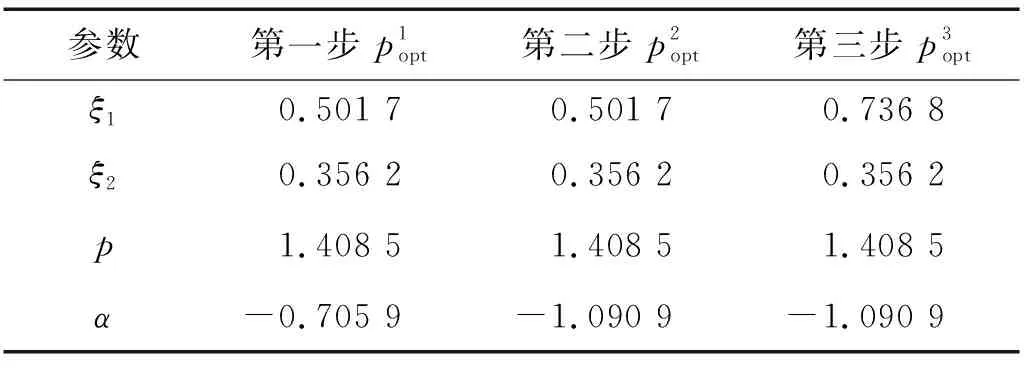
表2 最优结构参数Tab.2 Optimal structural parameters

3.1 稳定性验证

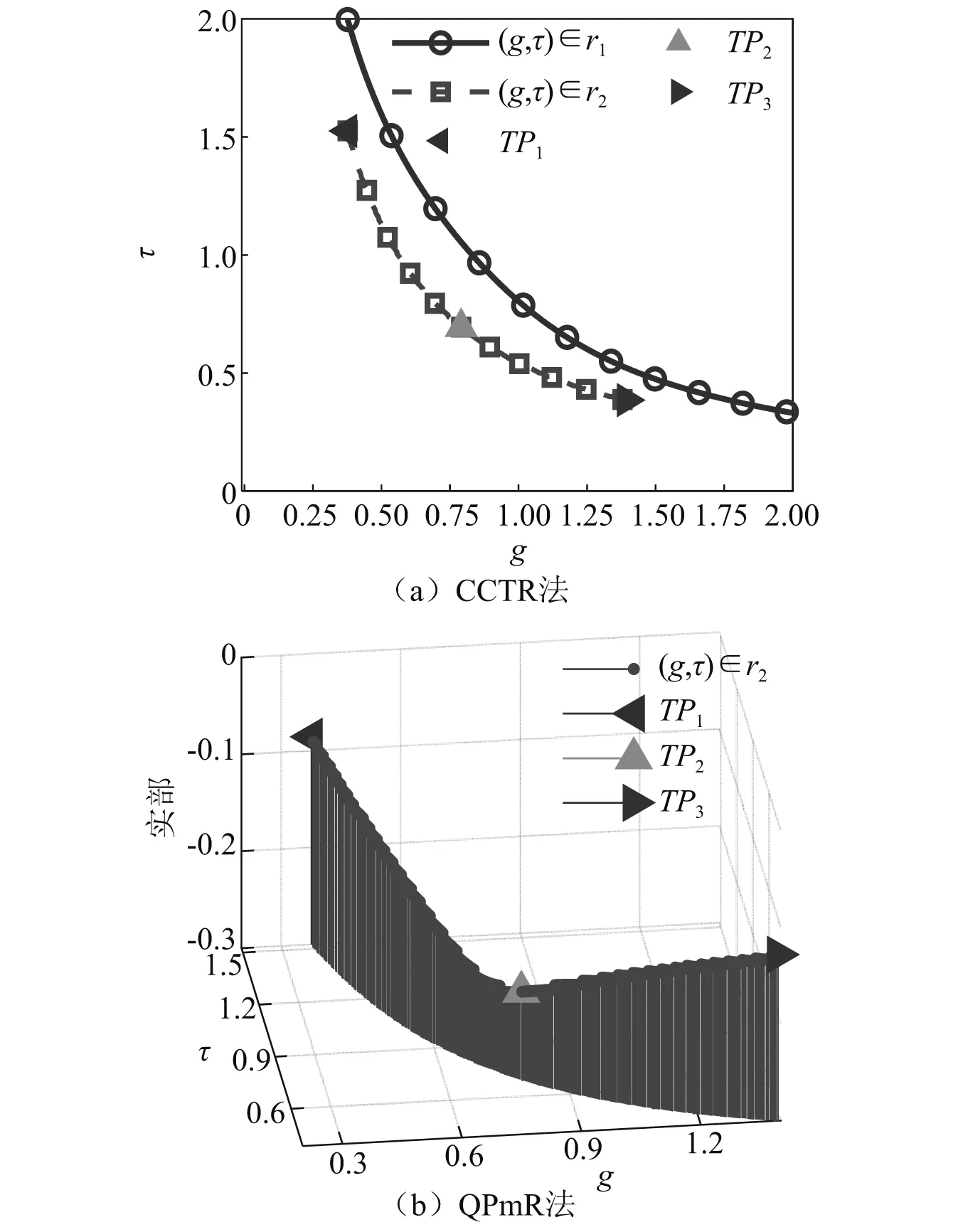
图10 结构参数下g和τ稳定区间Fig.10 The stable intervals of g and τ under the structural

3.2 频域验证

由图9可知,图10中标记的三个点TP1,TP2和TP2对应的反共振点频率分别是Ωa1=0.558 6,Ωa2=1.009 0,Ωa3=1.468 5。我们把TP1,TP2和TP2三个点对应的增益系数g和时滞τ代入式(7)所得三个点的幅频响应曲线,如图11所示。从图11中可知,三个验证点的反共振频率与图9中的大小相等,对应反共振点的幅值也与图9中的幅值A1相等。

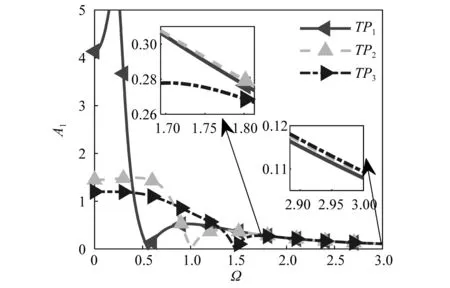
图11 TP1,TP2和TP3的幅频响应曲线Fig.11 The amplitude-frequency response curves at the points of TP1, TP2 and TP3

3.3 时域验证

对时域分析需要确定外激励频率,这里选择验证点TP1,TP2和TP3的反共振频率Ωa为外激励频率,用MATLAB软件中求解含有固定时滞的时滞微分方程的函数dde23来解方程式(3),得到三个验证点的时间历程响应曲线，如图12所示。从图12中看出,稳态解的振幅控制在0.01内。

图12 TP1,TP2和TP3的时间响应曲线Fig.12 Time-history curves at the points of TP1, TP2 and TP3

4 吸振器模型对比分析

为了证明时滞反馈控制反共振点优化方法的有效性,将本文结果与其他两种吸振器优化结果进行对比。

Asami等和彭海波等的最优结构参数用pA,pP表示,参数如表3所示。

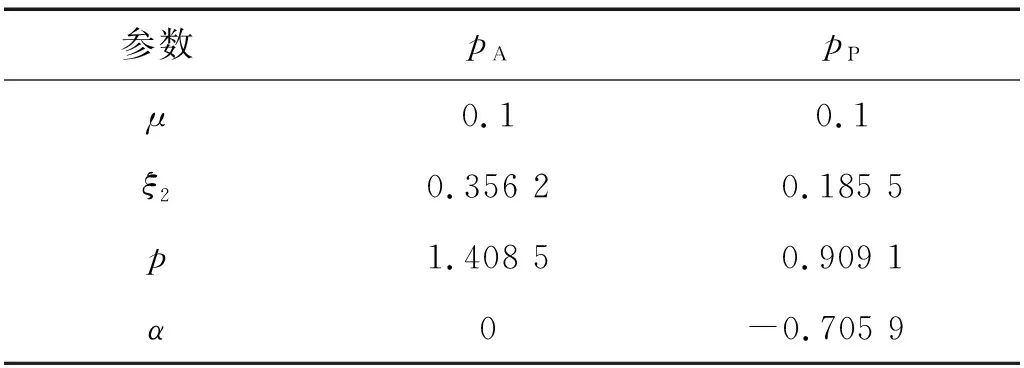
表3 Asami等和彭海波等的最优结构参数Tab.3 The optimal structural parameters of Asami’s and Peng’s

为了方便将本文结果与其他两种吸振器的减振效果进行定量对比,任选取一点TP2为例, 得到三种吸振器的幅频响应曲线，如图13所示。

图13 不同吸振器模型下的幅频响应曲线Fig.13 Amplitude-frequency response curves for different vibration absorber models

从图13可以看出,与Asami等的吸振器模型相比,在外激励频率大于0.532 3的情况下,本文的时滞负刚度吸振器具有很好的减振效果,不仅能够大大降低两个共振峰的幅值并且在反共振点处基本能够完全吸收主系统的振动;与彭海波等的吸振器模型对比,在整个频率区间上都具有很好的减振特性,同时反共振点处能够完全吸振。

为了定量地验证本文吸振器模型以及优化方法的可靠性,在反共振点附近的一段宽频区间内将三种吸振器模型的减振效果进行定量对比, 定义

式中：AA,AP,A1分别为Asami等、彭海波等和本文中的主系统的振幅；ρ1,ρ2为减幅百分比,如图14所示。

图14是本文模型分别与Asami等的模型和彭海波等的模型的主系统减振幅值百分比。从图14中可知，在反共振点附近主系统的减振效果最好,几乎达到100%;在反共振点附近的区间Ωa∈(0.6,1.8),最低减振幅值的百分比都在20%以上。