综合谐波算法的小电阻接地配电网高阻比率制动保护

倪江，孙昕炜，熊晓曼，任昊，杨宇玄

（1.国网四川省电力公司经济技术研究院，成都 610041；2.国网四川省电力公司电力科学研究院，成都 610041）

0 引言

近20 多年来，随着城市电网负荷迅速增长，电缆线路长度增长很快，逐步代替了架空线路，系统电容电流急剧增加，导致采用不接地或经消弧线圈接地的配电网系统因单相接地故障过电压烧坏设备的事故概率大大增加。为解决这一问题，许多城市经过分析与研究，逐步采用中性点经小电阻接地方式，例如广州和深圳配电网系统采用400 A 单相接地故障时接地电流、15 Ω 接地电阻（简称400 A，15 Ω）的接地方式，上海与北京分别采用1 000 A，5.77 Ω 和600 A，10 Ω 的相似接地方式。运行经验表明，小电阻接地方式对降低系统过电压水平以及提高系统可靠性具有良好的效果，可以降低设备的耐高压水平，故障时让保护可靠跳开故障线路，节省出线投资。

中性点经小电阻接地的配电网系统如果采用过电流保护、零序过流保护或零序功率方向保护，出线保护耐过渡电阻的能力比较低，一般不超过365 Ω［1］。小电阻接地配电网发生单相金属性接地故障时，零序过流保护能够快速切除故障，防止故障蔓延。但是如果发生高阻接地故障，接地点存在数值较大的过渡电阻，例如架空线经树枝、沙地等非理想导电介质接地，或者电缆绝缘水平下降引起间歇性电弧放电，可能导致故障电流小于传统过流保护的阈值而不能被保护装置检测和清除。高阻接地故障危害很大，数值不大的故障电流长期存在而不能被发现会酿成严重的后果，易引发故障点火灾、设备损坏以及人身伤亡等事故。

近几十年关于高阻接地故障的检测算法众多，包括基于电弧噪声的算法［2］、谐波算法［3-10］、小波算法［11-12］、智能算法［13］和基于零序电压比率制动的算法［14］。由于高阻故障具有显著的三次谐波特征，谐波算法是最为常用的中性点有效接地配电系统高阻接地故障检测算法，但其仅在间歇性电弧放电的情况下有较好的检测效果，应用受到一定限制［15］。基于零序电压比率制动的算法可以保证区内发生高阻接地（1 000 Ω左右）故障时保护能够可靠动作，同时区外发生任何故障时保护可靠不误动，兼顾了低阻接地故障和金属性接地时保护的灵敏性和高阻接地故障时保护的可靠性［14］，但该算法基于稳态量进行判断，在发生间歇性电弧高阻接地故障时灵敏度较低，且导纳制动系数K较难设定。

为解决这一问题，本文从高阻接地故障特征入手，总结了高阻故障电流及零序电流特征，提出综合零序电流谐波算法的高阻接地比率制动保护，并对该保护算法进行仿真测试。

1 小电阻接地配电网高阻接地故障特征

欧美国家配电网普遍采用中性点经小电阻接地方式，前期开展了大量的高阻接地故障检测研究。美国得州农业矿业大学（Texas Agriculture &Mining University，TAMU）于1977 年最早开展了高阻接地故障检测的研究。在大量现场试验和数值分析的基础上，从幅值、谐波特点和中性点电流故障等3方面总结了高阻接地故障的典型特征。

1.1 故障电流幅值特性

高阻接地故障最明显的特征是故障电流很小，故障点的电流可能只有系统正常运行时负荷电流的10%，甚至更低。配电网的负荷电流一般在几十到几百A。国外研究实验数据表明，不同类型的高阻接地故障电流的典型值介于0～75 A 之间，具体数值见表1［16］。

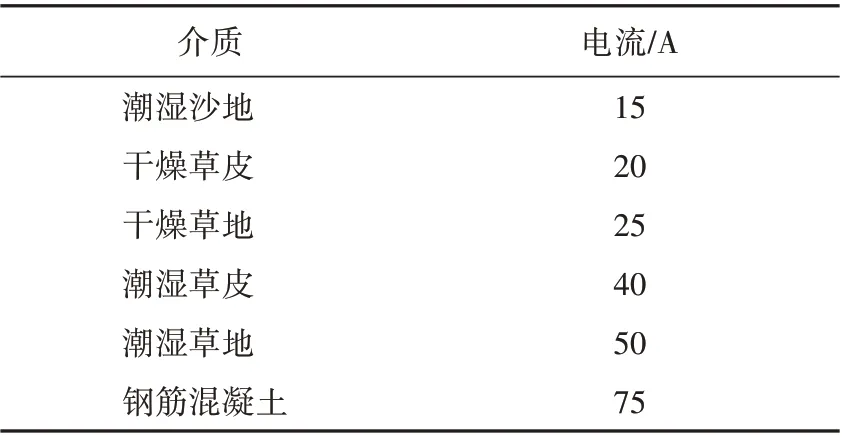
表1 12.5 kV高阻接地故障典型电流值Table 1 Typical HIF currents of a 12.5 kV system

以江苏某20 kV 出线保护的实际配置和整定值来分析，针对其单相高阻接地问题，如果采用零序过流Ⅱ段保护（按可靠躲过本线路电容电流整定），选用150 A 的整定值；如果采用零序功率方向保护（按躲过正常负荷的最大不平衡电流整定），不平衡电流整定值选取为30 A［1］；10 kV系统零序过电流保护整定值为60 A，此时系统的耐接地电阻能力仅为86 Ω［17］。无论采用零序过流保护还是零序功率方向保护，危害配电网一次设备或人身安全的单相接地故障经较大过渡电阻时，保护仍存在拒动的可能。

1.2 故障电流谐波特性

发生高阻接地故障的故障点经常会有电弧放电现象发生，最为著名的动态电弧模型为1939年提出的Cassie模型和1943年提出的Mayr模型。

由于故障电弧等接地电阻的非线性，导致故障电压、电流产生谐波畸变［18］。当电弧在电压过零点熄灭时空间温度较低，导致空气电阻较高，电弧电流减小到零后增长趋势比较缓慢；当电压升高到一定程度时，电弧重燃，空间温度升高，空气电阻降低，电弧电流增大到最大值的增长速率较快。电弧间歇性的熄灭和重燃与三次谐波叠加在基波上的效果相似，所以高阻接地故障电弧放电带有显著的三次谐波特性。另外，土壤中的二氧化硅等物质本身具也有非线性特征［19］。因此，故障电流中除工频分量以外还含有大量的谐波成分，如图1 所示。为了增加比对性，图2 中给出了Cassie 模型配电网故障仿真得到的电弧电流波形，还有高阻接地故障实验室测试得到的故障电流波形。

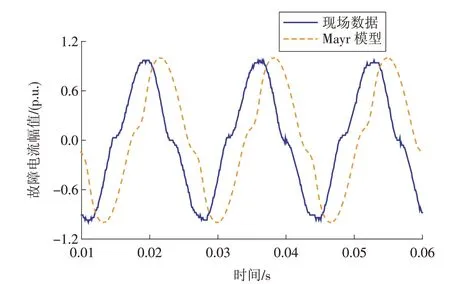
图1 高阻接地故障电流的谐波特性Fig. 1 Harmonic characteristics of HIF current

图2 故障电流仿真与现场测试波形Fig.2 Simulation and field data waveforms

将图2 中故障电流现场数据进行傅里叶分解，其基波频率为50 Hz，Hn为n次谐波含量，三次谐波含量H3高达10%。由分解结果可知，在有电弧存在的情况下，高阻接地故障电流中含有大量的谐波成分，特别是三次谐波。

1.3 中性点电流故障特征

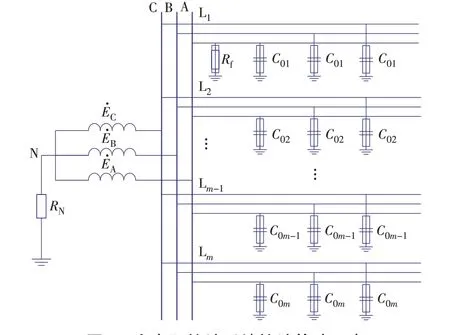
图3 小电阻接地系统接地故障示意Fig.3 Fault of the low resistance grounding system

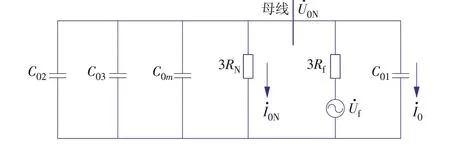
图4 零序网络Fig.4 Zero-sequence network

由式（3）可以看出，接地电阻Rf越大，变压器中性点零序电流I0N与故障点电流的基波幅值越小，两者均会随着接地电阻的增加而减小，变压器中性点零序电流和故障线路零序电流大小成正比。

高阻接地故障之所以难以检测，是由于其故障类型十分广泛，特征千差万别：比如很多高阻接地故障伴随电弧放电发生，但也有一些故障没有；有些故障中电气量有很高的谐波含量，但有些故障中谐波含量很低；有些故障变压器中性点零序电流较小，但有些故障中零序电流较大。高阻接地故障检测存在灵敏性和可靠性的博弈，任何单一的故障检测算法都不太可能检测到所有的高阻接地故障，因此多种方法协同，发挥各自优点，是高阻接地故障保护可靠性和灵敏度的必要手段［20］。

2 综合谐波算法的高阻比率制动保护

2.1 基本原理

考虑小电阻接地配电网高阻接地故障电流的各种特征，保护选择各线路出口处的零序电流基波幅值I01和变压器中性点零序电流I0N作为检测电气量，I01作为主判据量，I0N作为制动量，整定值根据制动电流自适应调整。

针对高阻接地故障电流微弱特征及变压器与线路零序电流的正比关系，在传统零序过电流继电器中引入制动量I0N，各线路出口处零序电流的整定值相比传统零序过电流保护适当下调，最低至各线路对地电容电流引起的最大不平衡零序电流，保证在区内发生不同接地电阻的情况下保护能够正确动作，而区外故障时保护始终不动，以此在保证保护可靠性的前提下提高系统的耐接地电阻能力。

针对有电弧存在的高阻接地故障电流谐波特性，各线路出口处零序电流的谐波含量应该作为保护判据的一部分，检测线路零序电流三次谐波I03的幅值是否超过一定比例的基波I01，检测线路I03与I01相位差，以区分健全线路与故障线路［16］，在线路发生间歇性电弧接地故障时提高保护的灵敏度。针对高阻接地复杂的故障特征，综合谐波算法和变压器零序电流比率制动的原理，能够提高保护的可靠性和灵敏度。

2.2 保护判据

按比率制动［21］的方法，一般采用变压器零序电流比率制动的零序过电流保护整定值作为判据，

式（5）为综合谐波算法的高阻比率制动保护整定取值方法，区内接地故障判据为：各线路保护安装处I01大于调整后零序过电流保护整定值Iset。

2.3 整定值及系数的设定

设定Iset.min1，Iset.min2，I0G的最小动作整定值应保证金属性接地或故障点接地电阻较小时有足够的保护灵敏度系数，高阻接地故障时能可靠动作，在存在一定干扰电流或区外线路接地时不误动。

Iset.min1，Iset.min2，I0G的设定与系统耐高阻能力等要求有关，系统耐高阻能力要求越高，Iset.min1，Iset.min2整定值越低。例如，当10 kV 系统需要1 000 Ω 耐高阻能力时，不计线路阻抗，单相高阻接地故障时流过故障线路的零序电流I01=EA/(3Rf+ 3RN)≈1.9(A)；为使算法检测到1 000 Ω 左右的接地电阻，考虑保护装置一般接入3 倍零序电流信号、K取1.3，保护整定值应设定为Iset.min2= 3I01/K≈4.5(A）。考虑故障电弧的存在，按躲过出线对地电容电流引起的最大不平衡零序电流整定，10 kV 系统电缆和架空出线最大不平衡零序电流分别为0.26 A 和0.37 A［14］，考虑3 倍零序电流和一定可靠系数，一般可设定

3 高阻接地仿真及结果分析

3.1 仿真建模

建立配电网高阻接地故障仿真电路如图5 所示，10 kV 配电网采用中性点经小电阻接地方式，线路参数见表2。

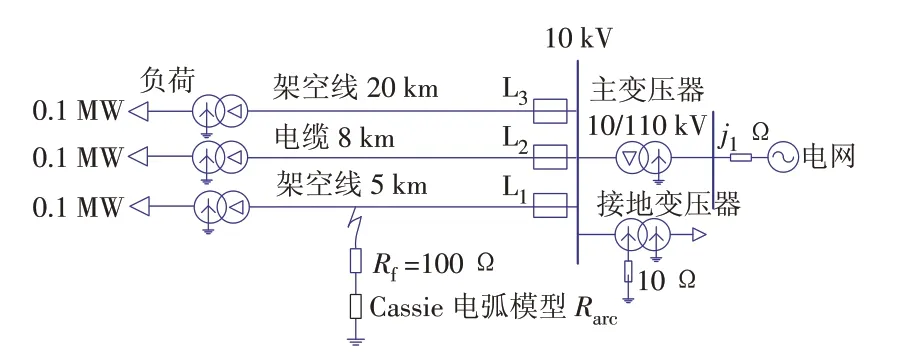
图5 配电网高阻接地故障仿真电路Fig.5 HIF simulation circuit

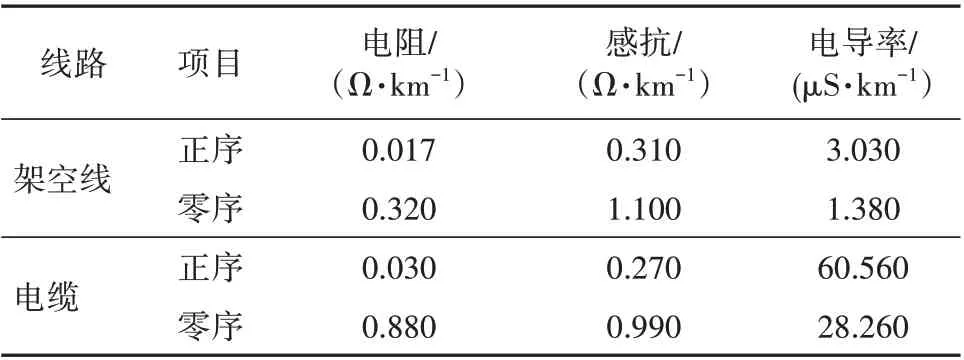
表2 线路参数Table 2 Parameters of the lines

Cassie电弧模型方程为

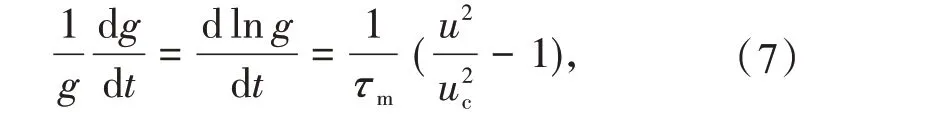
式中：g为电弧电导；u为电弧电压；τm为电弧时间常数；uc为电弧瞬态恢复电压。仿真中电弧参数取τm=0.000 6 s，uc=7 746 V。

以线路L1为例，安装综合谐波算法的高阻比率制动保护，并按以下4种故障类型进行仿真。

（1）金属接地故障（Rf=Rarc=0 Ω）。

（2）间歇性电弧高阻接地故障（Rf=100，500，1 000 Ω，Rarc使用Cassie模型）。

（3）纯电阻非时变高阻接地故障（Rf=100，500，1 000 Ω，Rarc=0 Ω）。

（4）区外故障（指线路L3中段发生金属接地故障）。

3.2 仿真结果及分析

以图5 中的Cassie 电弧模型建立微分方程，采取PSCAD 软件仿真、MATLAB 储存前一时刻电弧电压数值的方法，交互迭代。不同故障情况下PSCAD/EMTDC 与MATLAB 的交互仿真结果见表3，零序电流的变化如图6 所示，其中，故障类型分为a 金属接地故障、b 经电弧与1 000 Ω 电阻接地故障、c 经1 000 Ω 电阻接地故障，d 区域外故障。传统零序指零序过电流保护（整定值为60 A），谐波算法指基于三次谐波的高阻故障检测算法，电压比率制动指基于零序电压比率制动保护，本文算法指本文提出的综合谐波算法的高阻比率制动保护。

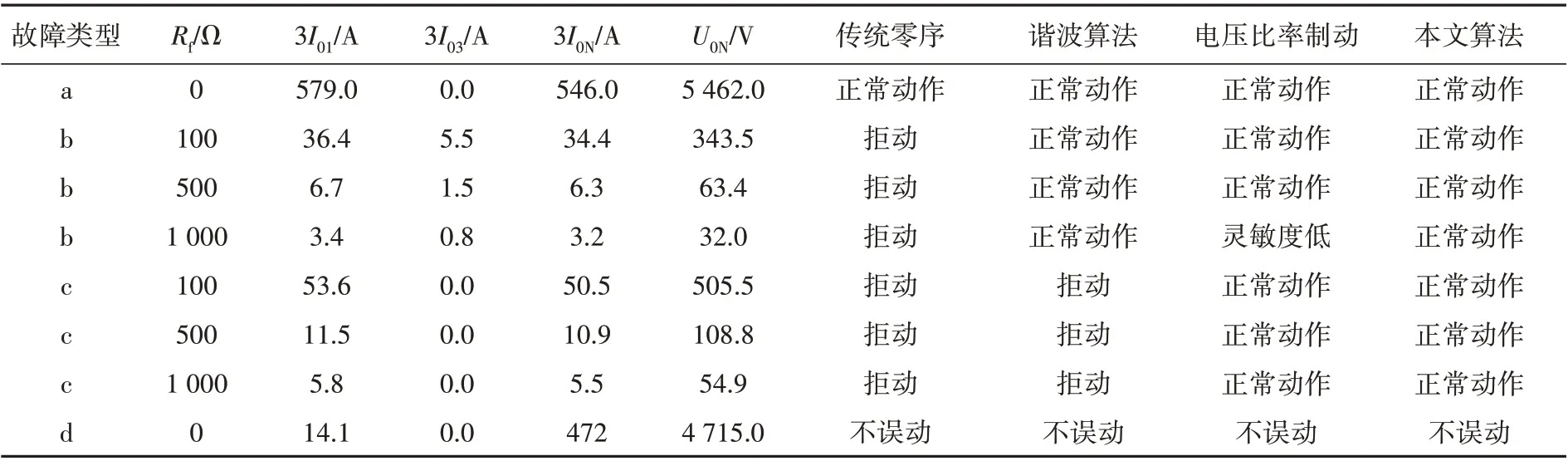
表3 仿真结果Table 3 Simulation results

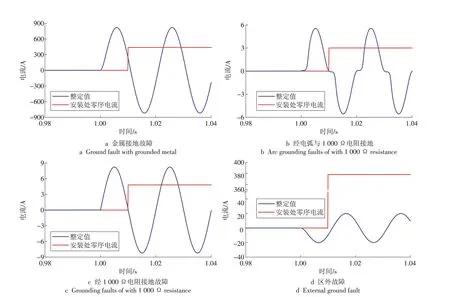
图6 故障线路零序电流仿真Fig.6 Fault line zero-sequence currents simulation

从表3可以看出：（1）传统零序过电流保护在金属接地故障情况下能够正常动作，区外故障时可靠不误动，但一旦出现间歇性电弧或高阻接地故障时，保护拒动；（2）谐波算法在金属、电弧接地和区外故障时动作正确，但无法应对纯电阻非时变高阻接地故障；（3）零序电压比率制动保护在各种故障下情况下表现良好，但在间歇性电弧高阻（1 000 Ω及以上）接地故障时灵敏度较低，甚至出现保护拒动；（4）对于综合谐波算法的高阻比率制动保护，将3I01，3I03，3I0N代入式（6），可以得出各种故障情况下的保护整定值，均动作正确。

在间歇性电弧和高接地电阻Rf（如1 000 Ω）同时存在时，线路零序电流三次谐波幅值I03占基波幅值I01较大的比例，I01较无电弧时更低，基于零序电压比率制动保护动作性能不够稳定，而谐波算法可以依据谐波条件继续调整最小动作整定值Iset.min1从而使保护可靠动作。

从图6 可以看出，对于综合谐波算法的高阻比率制动保护：（1）区内金属接地故障时，故障线路零序电流为579 A，大于保护的整定值437.2 A，保护正常动作；（2）区内经间歇性电弧与1 000 Ω 接地故障时，故障线路零序电流为3.4 A，大于保护的整定值3.0 A，保护正常动作；（3）区内经1 000 Ω 电阻接地故障时，故障线路零序电流为5.8 A，大于保护的整定值4.8 A，保护正常动作；（4）区外故障时，故障线路零序电流为14.1 A，小于保护的整定值378.0 A，保护不误动。

经过大量的仿真测试，选取不同故障位置、接地电阻值Rf、改变电弧及系统参数，保护均能正确灵敏动作，验证了算法的可靠性。

4 结束语

中性点经小电阻接地的配电网发生高阻接地故障，因故障电流微弱传统过流保护装置容易拒动。本文从高阻接地故障特征入手，总结了高阻故障电流及零序电流特征，提出了综合零序电流谐波算法的高阻比率制动保护，对整定值和系数进行了参考设定，保证了区内耐1 000 Ω 高阻和电弧故障的能力，仿真表明区内故障时保护算法均能正确灵敏动作，区外故障可靠不误动，有效提高了高阻故障检测的可靠性和灵敏性。