考虑多重不确定性的多站融合容量优化配置方法

2022-02-26路晓敏张明邓星王立伟陶以彬胡安平

综合智慧能源 2022年1期

路晓敏，张明，邓星，王立伟，陶以彬，胡安平

（1.国网江苏省电力有限公司南京供电分公司，南京 210000；2.中国电力科学研究院有限公司南京分院，南京 210000）

0 引言

随着我国分布式电网的发展，多站融合对于推进节能减排、建设信息化城市具有重要意义［1-2］。多站融合可将各类分布式电源、储能装置以及数据中心等负荷有效整合在一起，具有供电灵活、可近距离输电等优点［3］。多站融合的优化配置问题是多站融合规划、设计以及建设的核心问题之一，是保证多站融合经济、稳定运行的基础［4］，科学合理的配置方案对于降低建设成本、保障供电可靠性、提升可再生能源消纳水平具有重要意义。

多站融合优化配置问题是一个多目标、多约束、具有强非线性的复杂优化问题，传统的数学优化算法往往难以奏效，群体智能优化算法是解决该类问题最常用的方法［5］。文献［6］以满足负荷侧用电需求和可再生能源消纳最大化为原则，根据风-光-储系统的特点，提出了系统独立运行模式下的优化调度策略，并采用改进的仿电磁学算法对所建模型进行容量优化配置计算，得出了系统运行成本最低的容量优化配置模型。文献［7］在综合能源系统中充分考虑到储能的作用，建立了高效的园区综合能源系统优化控制逻辑框架，通过能源转化与分配，发挥不同能源的优势。文献［8］将多目标自适应差分进化算法对具有蓄电池容量的风/光/柴容量进行优化配置。文献［9］提出一种基于莱维和声搜索算法的容量配置多目标优化设计方法。

传统研究多站融合优化配置的方法没有考虑到设备中可再生能源的不确定性。考虑到多站融合系统内通常含有较多的风、光等具有不确定性的可再生能源发电，输出功率随机大范围波动，容易对电网造成冲击，影响安全、稳定供电，因此，需要考虑风、光资源的间歇性和随机性对多站融合优化配置结果的较大影响［10-11］。文献［12］在独立型光储供电系统优化配置中采用蒙特卡洛模拟法处理光照强度的不确定性；文献［13］通过概率密度函数的方法来研究风电的处理不确定性。文献［14］在独立型风光储系统优化配置中利用序贯蒙特卡洛模拟法处理风光和负荷的不确定性。文献［15］利用时间序列理论模拟了小型风储系统优化过程中风速的不确定性。

本文在考虑可再生能源不确定性的基础上，保证系统供电可靠性和新能源消纳的同时，建立以平准化能源成本为优化目标的多站融合容量优化配置策略，在量子引力搜索算法的基础上引入莱维飞行以进一步优化多站融合的配置。

1 多站融合优化配置模型

本文中提出的多站融合系统架构如图1 所示。其中，光伏电池板和储能电池分别通过各自的整流器或逆变器接入母线，通过控制单元给负载供电，图中AC，DC分别表示交流和直流，光伏产生的直流电流和储能电池中的直流电流通过DC/DC 模块转变直流输出电压并接入控制单元，风机产生的交流电流通过AC/DC 模块转变为直流电流接入控制单元。

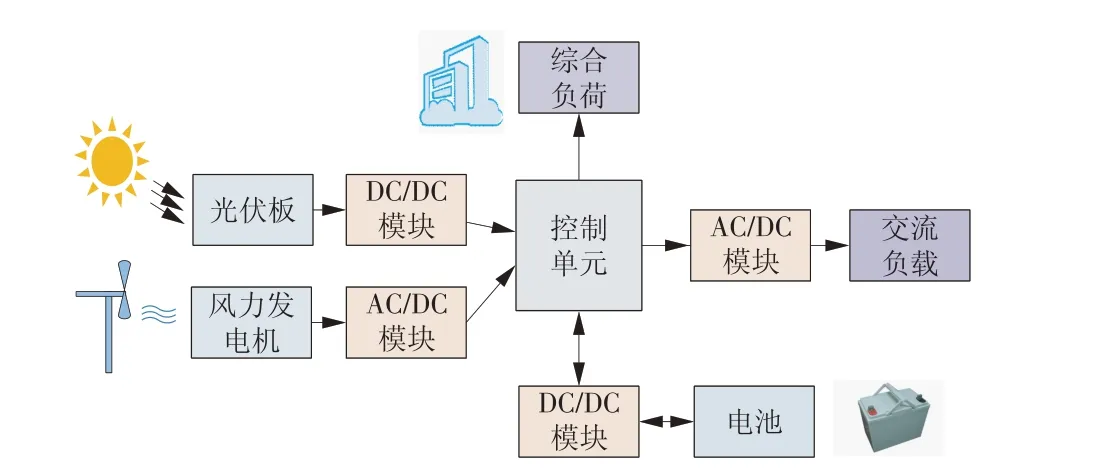
图1 多站融合系统简化模型Fig.1 Simplified model of the multi-station integration system

1.1 风力发电系统模型

一般认为风速的概率模型服从两参数的韦伯（Weibull）分布。假设v表示风速的随机变量，其服从用ω(k，c)表示的Weibull 分布，其概率密度函数为

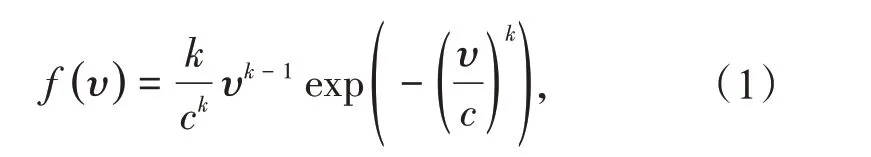
式中：exp 为以e 为底的指数函数；k为Weibull 分布曲线的形状指数；c为规模指数，计算如下

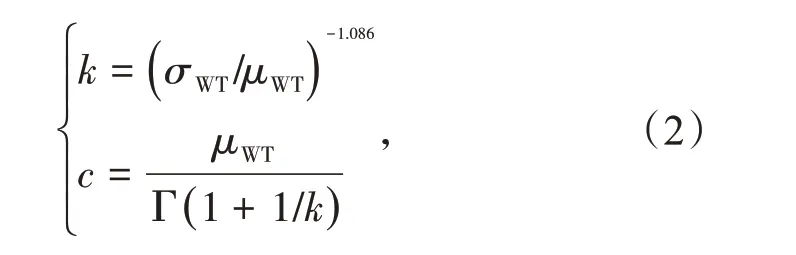
式中：μ和σ分别为风速平均值和风速标准差。

1.2 光伏发电系统模型

光伏发电系统输出的概率模型主要由光照强度的概率模型和基于光照强度的光伏输出模型2部分构成［16-17］，据统计，光照强度在一定时间段内近似服从贝塔分布（Beta，指一组定义在（0，1）区间的连续概率分布），其概率密度函数可表示为

1.3 综合负荷概率模型

由于用户用电的随机性，多站融合系统中的负荷功率可视为1个随机变量，相关研究表明，负荷的随机性近似服从正态分布，则可得负荷的概率密度函数为［18］

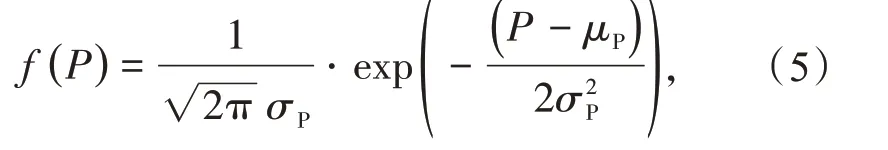
式中：σP为系统负荷变化方差；μP为系统负荷的数学期望值。

2 目标函数及约束条件

2.1 目标函数

文中以光伏板数量NPV和蓄电池个数NBAT作为优化变量，在保证系统供电可靠性的前提下，以平准化能源成本（Levelized Cost of Energy，LCOE）最小为优化目标，即

式中：CI，COM，CR，CS分别为系统各组件的初始投资费用、运营维护费用、置换费用和设备残值；r为实际贷款利率；n为系统工程寿命周期。

2.2 约束条件

（1）装机容量约束。

式中：m 为给定时间内系统不能满足负荷需求的采样点个数；LPSPmax为负荷最大允许缺电率，为了保障供电可靠性，本文限制多站融合的年功率缺额总量不能超过系统年总负荷的0.1%。

（5）能量溢出比约束。能量溢出比（Energy Wastage Rate，EWR）指在时间T内系统溢出的能量与可再生能源发出总能量的比值，通常情况下，能量溢出比在一定的允许范围即可，即

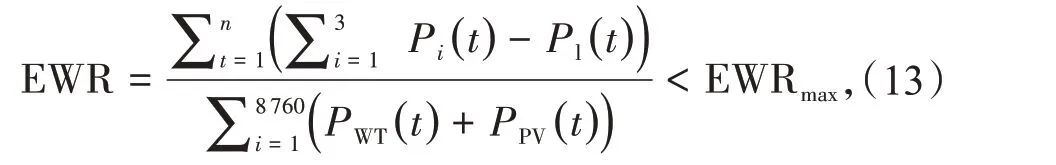
式中：n为给定时间内系统能量浪费的采样点个数；EWRmax为系统最大允许浪费率，为了保证可再生能源的消纳水平，本文取20%。

3 算法模型

3.1 量子引力搜索算法

量子万有引力搜索（Quantum inspired Gravitational Search Algorithm，QGSA）算法是量子计算与万有引力搜索（Gravitational Search Algorithm，GSA）算法的结合。在GSA算法中，粒子间通过引力作用实现优化信息共享，质量较小的粒子朝向质量较大的粒子运动，以此来搜索整个解空间。在QGSA 中，粒子一般通过薛定谔方程进行位置更新，QGSA算法过程描述如下［19］。

步骤1：初始化粒子位置。算法相关参数（主要包括算法迭代次数、种群数量、变量维数等）。假设在维搜索空间内随机生成N个粒子，其中粒子的位置可表示为

式中：c1，c2表示[0，1]之间的随机数。

运用蒙特卡洛模拟方法，可得粒子的位置更新公式

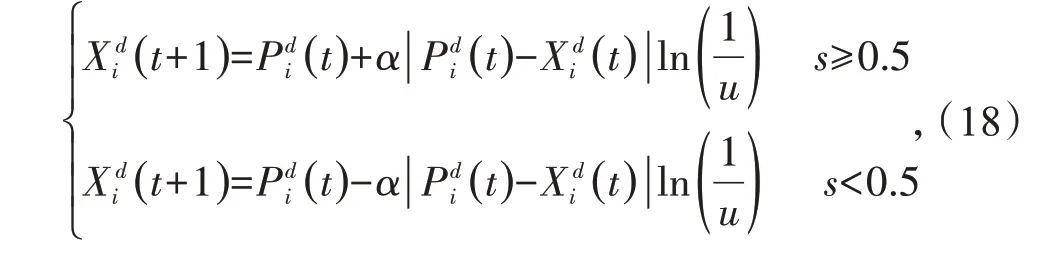
式中：s为［0，1］之间的随机数；α表示收缩扩张系数（Contraction Expansion，CE）。

步骤6：迭代操作。重复步骤2—5，直至达到最大迭代次数后终止。

3.2 改进量子引力搜索算法

3.2.1 CE系数动态调整策略

算法的控制参数对算法有着极大的影响。在QGSA 算法中，除了所有智能优化算法都需要设定的参数（例如迭代次数，种群大小和维数等）外，体现QGSA 算法自身特性的参数只有收缩扩张系数α。由式（18）可以看出，α取值的不同，直接影响粒子的位置更新。为此，本文引入一种收缩扩张系数的自适应动态调整策略，使粒子既能保证前期搜索的多样性，又能兼顾后期搜索的精细化。其表达式为

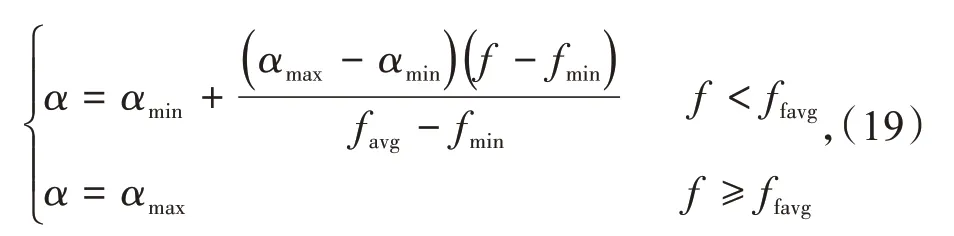
式中：αmax和αmin表示α的最大、最小值，根据文献［20］选取α的最大值和最小值分别取1.0和0.5；fmin和fmax分别表示当前所有粒子的最小适应度值和平均适应度值。

3.2.2 莱维飞行

由式（14）可以看出，势阱中心被限制在个体局部最优位置pbest和种群全局最优位置Mbest构成的超矩形阵中，若此时Mbest刚好陷入局部最优位置，则会造成算法早熟收敛。基于此，引入莱维飞行对全局最优粒子进行更新扰动，进一步提高算法搜索能力。

莱维飞行由法国数学家Lévy 提出，是一种服从莱维分布的随机游走搜索策略［21］，其位置更新式为

Xi(t+ 1)=Xi(t)+α0⊕Lévy(λ)，i= 1，2，…，n，（20）

式中：Xi(t)为Xi第t代位置；⊕为点对点乘法；α0为步长控制量。Lévy(λ)为参数为λ的随机搜索路径，表达为

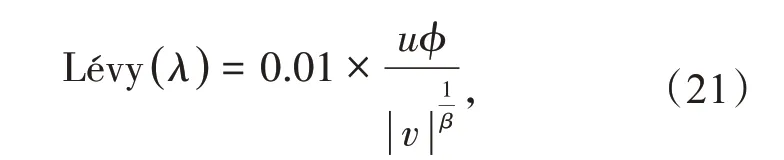
式中：u，v都服从标准正态分布；β为控制分布的变量，一般取［0，2］之间，本文取1.5。ϕ表示方差，其表达式为

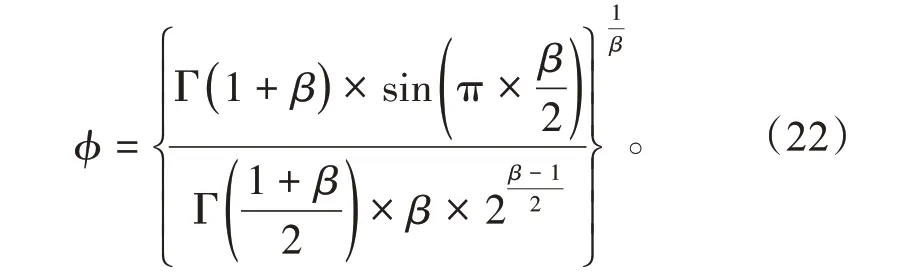
由上述可以看出，莱维飞行具有幂率分布和广义中心极限定理的特点，故而将莱维飞行与优化算法的有机结合能够有效扩大粒子搜索范围，增强算法寻优性能。莱维飞行搜索本质上是将步长随机化模拟飞行的方法，其步长呈现以小步长结合大步长的特点，将此特点用于QGSA，可以有效提高粒子搜索能力，从而使优化算法能够更容易跳出局部最优解位置。

3.3 蒙特卡洛模拟

多站融合系统中由于光照强度以及负荷的随机性和不确定性，常规的模型只能模拟特定时刻的出力，并不能很好的模拟一段时间的系统出力情况，在多种模拟仿真方法中，蒙特卡洛随机模拟［22］（MCS）是目前电力系统较为常用的模拟仿真方法。MCS 是一种基于概率统计理论的仿真算法，能够有效处理系统不确定性因素的影响，尤其适用于出力不确定性因素较多、较复杂的情况。是一种采用抽象理论近似地求解物理或数学问题的方法，它可同时处理多个变量，基本思路如下。

（1）建立所研究问题的数学模型，确定模型中不确定变量的分布特性。（2）按照不确定变量的分布特性，生成随机数。（3）计算随机数序列的目标函数值，作为模拟试验值。

（4）统计和处理数据。

本文通过将MCS 嵌入QGSA 算法中，用于求解多站融合容量优化配置问题，优化配置流程如图2所示。

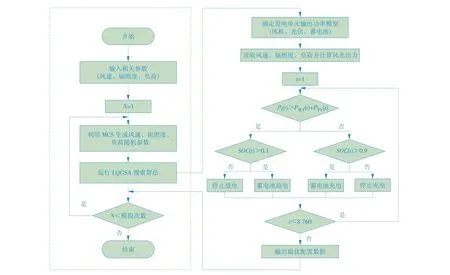
图2 基于LQGSA-MCS的容量优化配置流程Fig.2 Flow of the optimal capacity configuration based on LQGSA-MCS

4 算例分析

4.1 仿真数据

为验证本文提出的优化配置模型和方法的有效性，利用美国航空航天局（National Aeronautics and Space Administration，NASA）数据库，选取某地区（经度120.86°，纬度32.01°）进行容量优化配置。该地区全年8 760 h 的地面辐照度及电力负荷需求如图3所示。

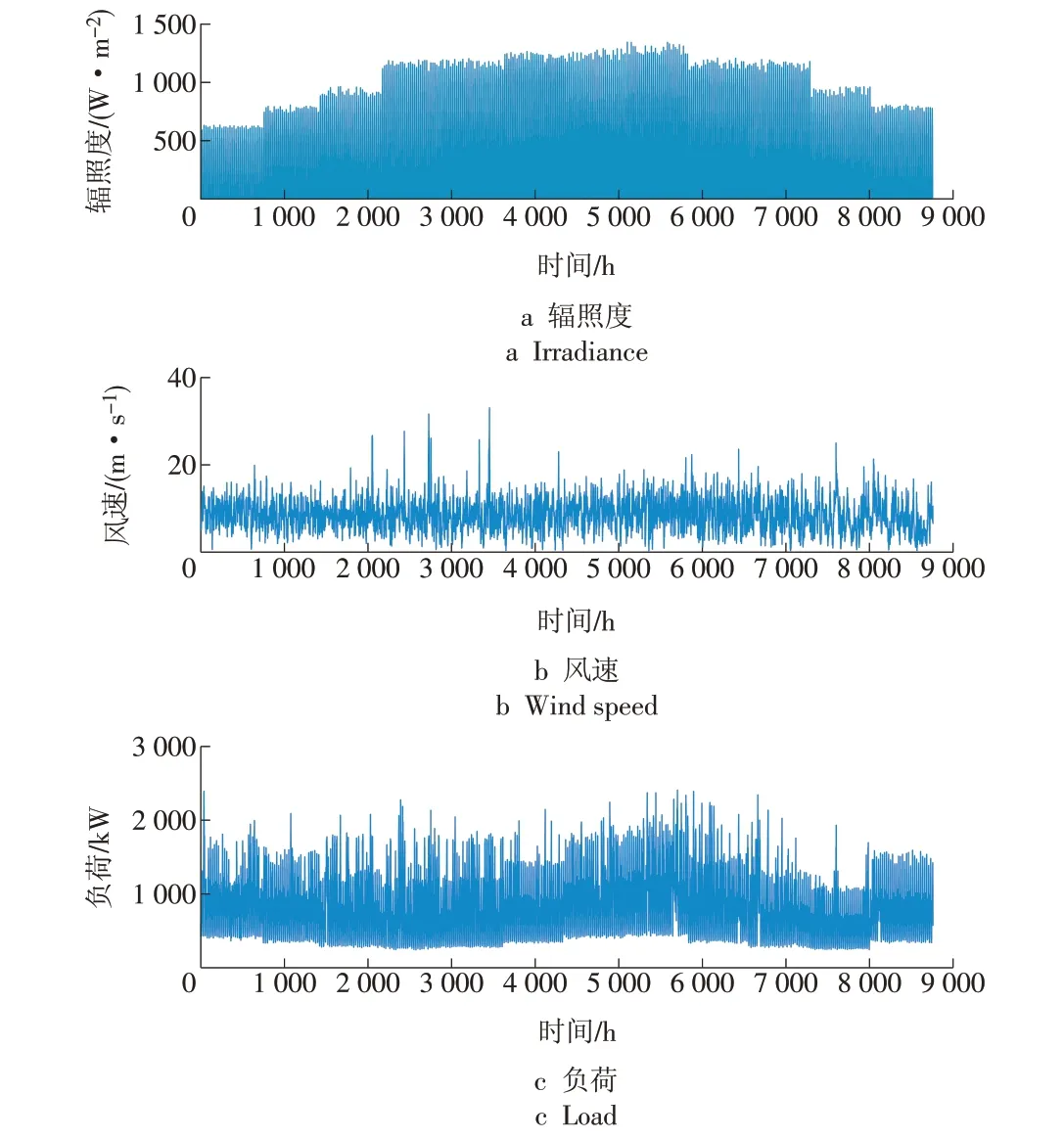
图3 风速、辐照度及负荷年数据曲线Fig.3 Annual data curves of Wind speed，irradiance and load

设定系统优化规划使用年限为20 a，各类待选电源型号及相关参数见表1。

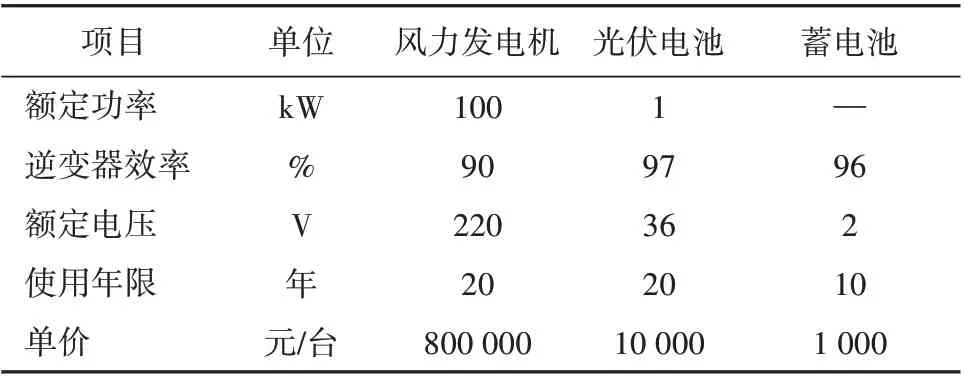
表1 各类待选电源参数Table 1 Types of alternative power sources

4.2 仿真结果分析

依据本文所建各电源的数学模型和经济性模型，采用本文提出的LQGSA-MCS 与QGSA-MCS、PSO-MCS［23］（PSO 为粒子群优化算法）方法在求解多站融合容量优化问题上进行对比。3 种方法的约束条件、种群规模、迭代次数等参数设置均一致。设定种群规模N= 50；最大迭代次数为200，抽样次数为1 000。

3 种算法优化对比结果见表2。由表2 可知，在1 000 次的统计过程中，由LQGSA-MCS 算法求解系统LCOE 均值为0.79 元/（kW·h），为QGSA-MCS 算法求解均值0.81 元/（kW·h）的97.53%，为PSOMCS算法求解均值0.90元/（kW·h）的87.78%，可见LQGSA-MCS 算法求解精度最高；就稳定性而言，LQGSA-MCS 算法求解结果下的系统风机、光伏、蓄电池的容量配置及LCOE 标准差均为3 种算法中最低，可见所提算法稳定性明显优于另外2种算法；就运行速度而言，LQGSA-MCS 运行时间均值为9.53 s/次，低于QGSA-MCS 的10.07 s/次和PSO-MCS 的10.89 s/次，可见所提算法运行速度优于另外2 种算法。由此可见，本文所提LQGSA-MCS 算法对于求解计及源荷不确定性的容量优化配置问题效果优于QGSA-MCS和PSO-MCS 2种算法。

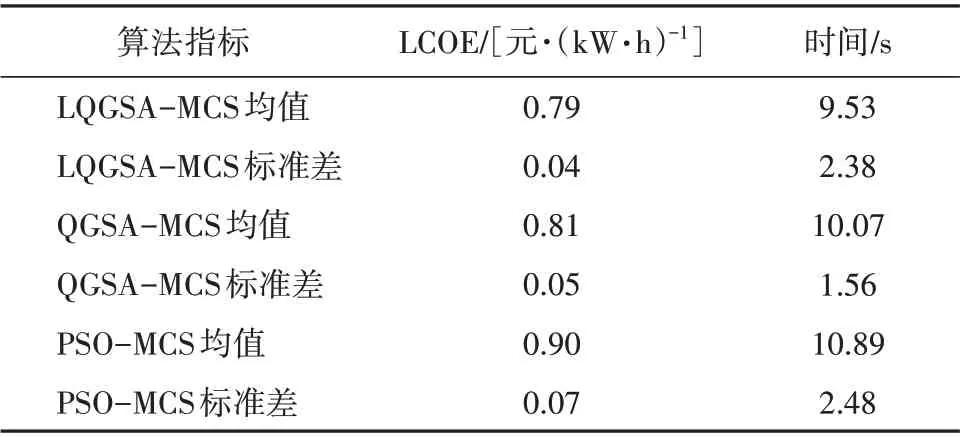
表2 不同方法优化结果对比Table 2 Comparison of different optimal configurations

在风机、光伏、负荷的波动情况下，不同方法下LCOE 频率分布及累计概率密度如图4 所示。通过对比可知，LQGSA-MCS 求解下LCOE 出现频次最高为0.7 661 元/（kW·h），低于QGSA-MCS 的0.8 014元/（kW·h）和PSO-MCS 的0.8 964 元/（kW·h）。同时，LQGSA-MCS 求解系统LCOE 波动在0.72～0.93元/（kW·h）之间，区间长度为0.21 元/（kW·h），为均值的26.58%；QGSA-MCS 求解LCOE 波动范围为0.72～0.96 元/（kW·h），区间长度为0.24 元/（kW·h），为均值的29.63%；PSO-MCS 求解LCOE 波动为0.74～1.13 元/（kW·h），区间长度为0.39 元/（kW·h），为均值的43.33%。由此可见，LQGSA-MCS 求解结果下的LCOE 预测风险度最低，且3 种方法求解的LCOE 的频率分布图与正态分布曲线的契合度充分验证了本文模型和算法的可行性和可靠性。

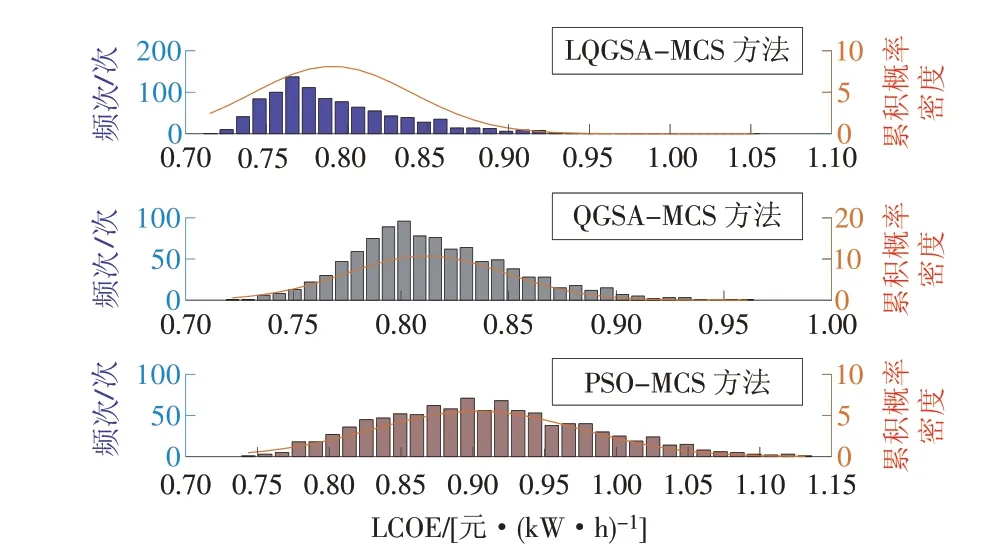
图4 不同方法下LCOE频次分布及累计概率密度Fig.4 Frequency distribution and cumulative probability density of LCOE with different methods

研究系统平准化能源成本与模拟次数之间的关系，结果如图5所示。从图中可以看出，当模拟次数达到1 000 次时，3 种算法模拟样本的均值已达到或接近稳定状态，说明1 000 次抽样次数足够，且说明本文提出的算法收敛性良好。同时，在1 000 次统计过程中，LQGSA-MCS 算法求解LCOE 收敛精度明显优于另一种算法。

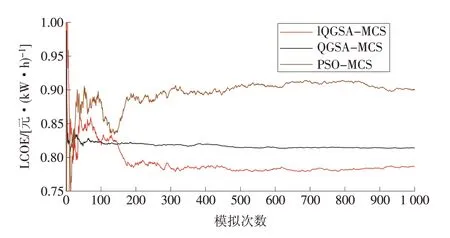
图5 不同模拟次数下计算结果Fig.5 Calculation results under different simulation times

4.3 敏感性分析

为了对本文所提多站融合系统进行深入研究，针对LQGSA 设计的多站融合系统进行敏感性分析，以深入了解不同优化变量或参数对系统平准化能源成本的影响。对光伏电池成本、蓄电池投资成本、负荷需求、太阳能资源等输入参数进行了敏感性分析。计算参数值偏离20%对LCOE 结果的影响，结果如图6所示。

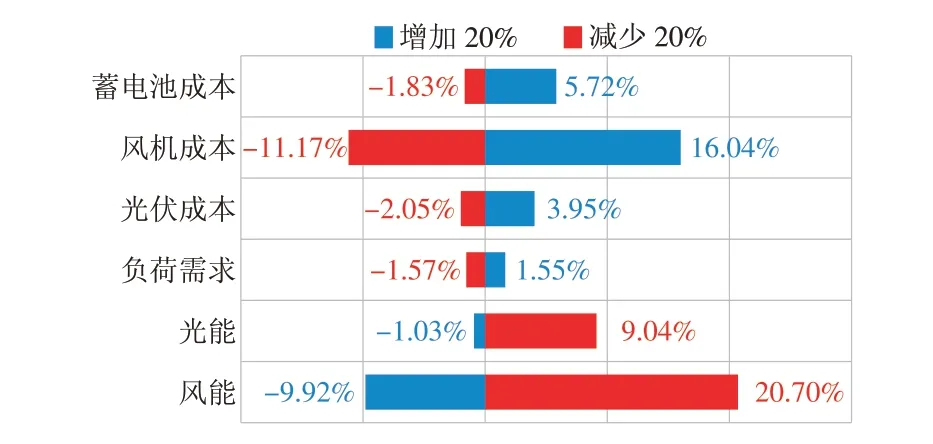
图6 关键参数的敏感性分析结果（影响因素为±20%）Fig.6 Sensitivity analysis results of the key parameters（influencing factor=±20%）

对比图6 结果可以看出，风速减少20%，LCOE增加20.70%，风速增加20%，LCOE减少11.17%，可见风速的偏离对LCOE 影响较大；且风机成本的改变对系统平准化能源成本的影响也相对明显，风机成本增加20%，直接导致LCOE 增加16.04%。同样，光照强度的减少对LCOE 的影响也很明显，相反，光照强度的增加对LCOE 影响较小，且光伏电池成本的变化对系统影响相对较小。值得注意的是，负荷需求的改变对系统成本影响不大。总体而言，风力发电是决定系统容量和成本的关键参数。