密度梯度驱动的煤粒瓦斯解吸扩散模型及试验研究

2022-02-26秦跃平张凤杰

煤炭科学技术 2022年1期

秦跃平，徐浩，毋凡，张凤杰

(中国矿业大学(北京)应急管理与安全工程学院，北京 100083)

0 引言

随着我国煤炭资源开采深度的逐步增加，瓦斯涌出量及强度增大，会诱发更多的瓦斯超限、瓦斯突出等瓦斯灾害问题[1-2]。在深部煤层高强度开采阶段，煤体的瓦斯解吸速率会更快，瓦斯释放特性会更加复杂。因此，深入认识并理解煤体中的瓦斯解吸扩散规律对于精确计算预测井下瓦斯含量、瓦斯涌出量以及瓦斯解吸指标等工作至关重要。

为了从理论上解释煤粒中的瓦斯解吸扩散机理，菲克扩散理论[3]首先被提出来，并且产生了广泛而深刻的影响。在此基础上，出现了单孔扩散模型[4-5]、双孔模型[6-7]，用来表述瓦斯扩散特性及规律。经典菲克单孔扩散模型由于其计算简单、物理意义明确的特点受到了人们的青睐，也是目前沿袭最为普及的扩散模型[8-9]。国外学者BARRER[4]、CRANK[5]等根据菲克扩散模型建立了相应的数学方程，并且提出了有关解吸扩散量的解析解公式。后续国内学者杨其銮等[10]、聂百胜等[11]基于此对经典菲克扩散模型进一步简化推导，得到了模型的近似解析解，由此可以便利地计算常扩散系数。这也是目前获取煤粒中的瓦斯扩散系数的常用办法。但是这些由经典扩散模型简化导出的近似解析解公式与解吸扩散试验数据存在较大偏差，并不能很好地描述全时段瓦斯解吸扩散行为[12]。如此一来，像扩散系数这类工程参数的测定准确性也就无法保证。不少学者试图将扩散系数随时间变化的表达式引入经典菲克扩散模型，用以保证预测结果与试验数据相一致[12-14]。但是这种方式违背了菲克模型最初的常扩散系数的基本假设，而且文献[15]也指出目前还没有足够的物理基础来证明空间内均匀的扩散系数确实是随时间下降的。文献[16-18]主张用达西定律或者反常扩散理论来描述煤粒瓦斯扩散过程。虽然也获得了不错的试验匹配结果，但是在适用性、物理意义及推广应用等方面也存在一些争议[12]。另外，根据实验室条件下的煤粒瓦斯解吸数据表现出的扩散规律，涌现出了许多形式简单的解吸经验公式[19-20]。各解吸经验公式由于适用条件不同，所造成的误差也各异。就目前来看，没有一个经验公式能够准确表征各类条件下的全时段瓦斯解吸过程。上述研究已经从一定程度上表明菲克理论模型似乎不再适合用来描述煤粒瓦斯扩散行为。因此，亟需建立一个更加科学的而且能在整个时间尺度下准确描述煤粒瓦斯扩散过程的理论模型。

实质上，菲克扩散模型认为瓦斯在煤粒中的流动过程是由浓度梯度驱动的，其所谓的浓度就是煤粒瓦斯含量，并且没有区分开吸附态和游离态瓦斯含量。而在煤粒瓦斯解吸扩散试验中，主要参与流动的实际上是游离瓦斯[21-22]。在此基础上，笔者首先在4种初始解吸压力下开展瓦斯解吸试验，并提出了由游离瓦斯密度梯度驱动的煤粒瓦斯扩散新模型。将新扩散模型的数值解算结果与试验数据对比，并探讨了新扩散模型相对于经典菲克模型的优势，目的是进一步验证新扩散模型的精确性、普适性以及先进性。

1 解吸扩散试验

1.1 煤样选取与制备

试验采用的是云南宣威县大菁煤矿的煤样。尽可能地将现场采集到的新鲜大块煤样密封保存良好，并运送到实验室以开展试验。将煤块在105 ℃的温度下烘干后做初步干燥处理，之后冷却至室温。将煤样用粉碎机粉碎成煤粒后，使用标准样品筛筛选出0.100～0.118 cm粒径的煤粒来进行试验。每组试验均统一称取50 g煤样，并放入真空干燥箱中去除水分，以备试验使用。

1.2 试验过程

使用H-Sorb型高温高压吸附仪，具体试验系统及结构如图1所示。该装置主要由样品预处理区和煤样等温吸附试验区组成。装置通过高精度软性控温装置实现恒温条件下的瓦斯解吸试验。另外该装置的数据收集系统经由C++编程，具有较高的灵敏度，能够精确记录并计算瓦斯压力、吸附量及解吸量等数据。具体的试验步骤如下：①气密性检验：对试验装置进行气密性检测，直至气密性达到要求之后开展试验；②自由空间体积计算：采用真空充氦气的措施计算出样品罐中包含煤粒孔隙在内的自由空间体积；③瓦斯吸附过程：对整个试验系统进行抽真空处理，接着向参考罐中充入瓦斯气体，打开参考罐和样品罐的控制阀门，向样品罐通入瓦斯。当样品罐的压力维持稳定时，煤粒中的瓦斯达到吸附解吸平衡状态，记录此时的平衡压力值(即初始解吸压力)。④瓦斯解吸过程：瓦斯吸附达到平衡状态后，对样品罐抽气至一个大气压，关闭样品罐的通气阀门，使煤样在封闭空间自由解吸。观察并且记录试验过程中的压力变化，待到样品罐的瓦斯压力保持平稳时，解吸试验完成。根据相邻2个时刻的瓦斯压力数据可以计算单位时间内单位质量煤样瓦斯解吸量[21]，将其相加就能得到累计瓦斯解吸量。

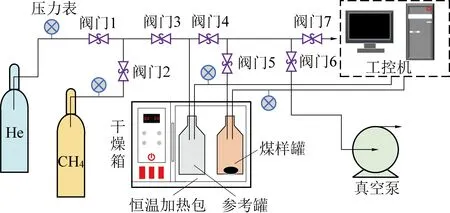
图1 试验系统结构

1.3 试验结果与分析

1.3.1 解吸量随时间的变化规律

煤样的累计解吸量随时间的变化趋势如图2所示。在试验的时间尺度范围内，煤样中的瓦斯解吸量总体随初始吸附瓦斯压力的升高而增大。初始吸附瓦斯压力越大，煤粒中瓦斯解吸速率也越快。

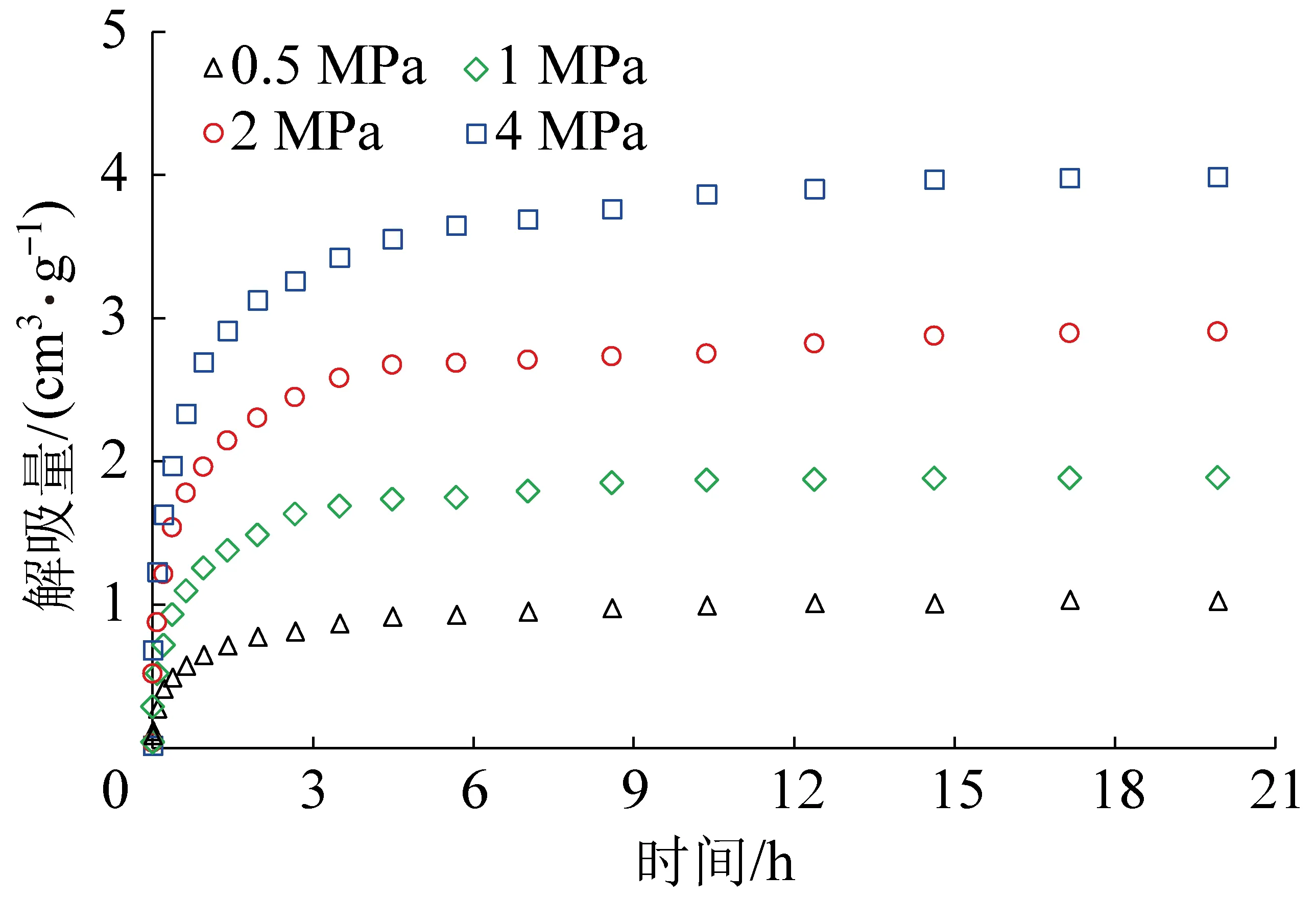
图2 不同初始压力下各煤样解吸量变化

1.3.2 解吸经验公式拟合效果

众多学者对煤粒中的瓦斯解吸量随时间的变化规律进行了试验研究，并且依托各自所获得的试验数据提出了许多解吸经验公式。某些经验公式存在一些局限性，难以全面并精确地描述解吸量随时间的变化趋势[19]。基于试验数据，选取了巴雷尔式[4]、王佑安式[23]、孙重旭式[24]以及秦跃平式[22]等部分经验公式来拟合瓦斯解吸数据，所用经验公式见表1。

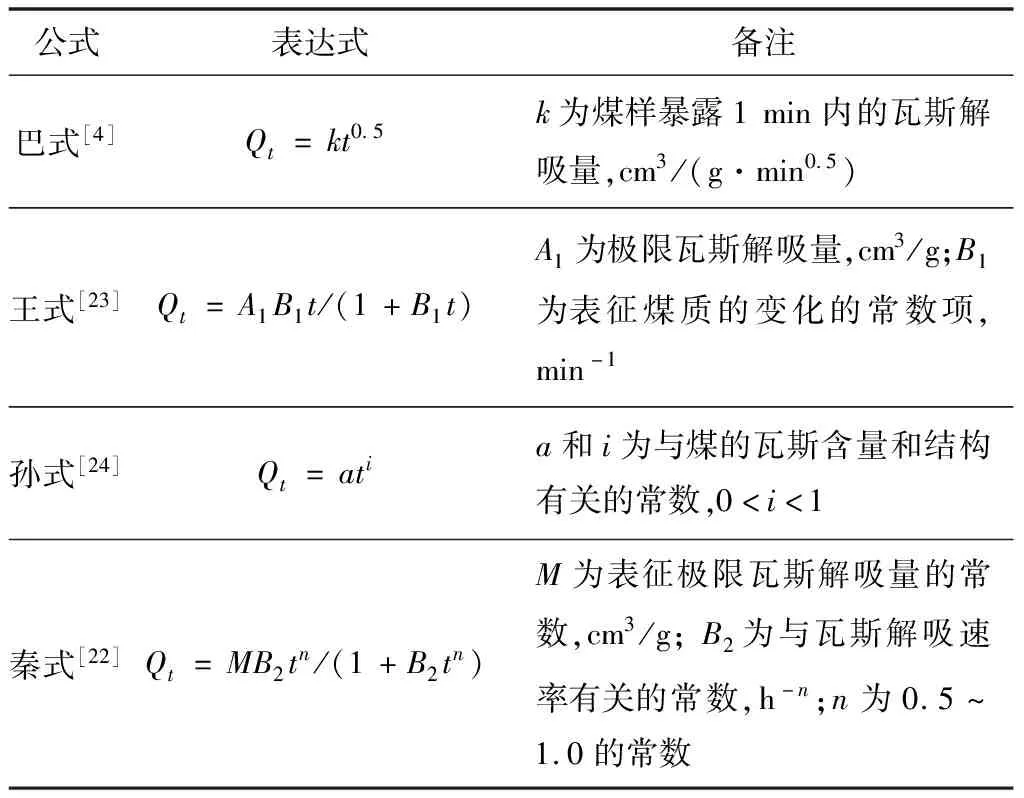
表1 瓦斯解吸经验公式

为避免冗余，仅以煤样在0.5 MPa压力下的试验数据为例，来展示各经验公式的拟合情况，如图3所示。通过各自的拟合结果发现，秦跃平式的拟合相关性系数R2最接近于1，说明其能够较准确表征煤粒瓦斯解吸过程。相对来说其他经验公式的拟合效果要差一些。

图3 解吸试验数据的拟合过程

为进一步直观观察秦跃平式与瓦斯解吸试验数据的拟合效果以及精确度，将表1中的秦跃平式变形为：

(1)

依照式(1)对解吸试验数据进行处理，即以解吸量的倒数为y轴，以时间函数倒数(1/tn)为x轴作图，具体如图4所示。式中n的取值为0.5～1.0，就试验煤样来看，图4中n的取值为0.66。通过图4更直观地看出，不同压力尺度下的秦跃平式的拟合相关性系数R2均大于0.99，可以说其是能够较为精确描述瓦斯解吸量随时间变化的经验公式之一。

图4 解吸量倒数与时间函数倒数关系曲线

2 煤粒瓦斯扩散模型及解算

2.1 浓度梯度驱动的菲克扩散模型

煤粒中瓦斯的解吸扩散行为一直是一个广泛而深远的研究课题。最初瓦斯在煤粒这种多孔介质中的扩散被认为是符合菲克扩散理论，表述为单位时间单位面积的分子扩散流通量与浓度梯度成正比[3]：

J=-Dgradc

(2)

式中：J为扩散质量流量，即单位时间单位面积上流过的瓦斯质量，g/(s·cm2)；D为扩散系数，为常数值，cm2/s；c为单位体积煤体的游离和吸附瓦斯含量，g/cm3。

许多学者对以菲克扩散理论为基础的模型进行了深入探索，并推导出了球形颗粒经典菲克扩散模型的理论解及近似解析解，依此能便利地求解扩散系数[5, 11]。但是这些解算结果只能在特定的时间段与试验数据保持一致，在对整个时间段的瓦斯解吸扩散特性表征方面却无能为力[12]。有文献指出为得到解析解，菲克模型放宽了许多假设条件，这也有可能导致预测结果不准确，数值解相对来说会比解析解更合理[25]。笔者基于有限差分的数值方法对菲克解吸扩散数学模型进行了解算，封闭空间内的瓦斯解吸扩散微分方程可表示[21]为

(3)

式中：r为极坐标半径，cm。

初始条件和边界条件为

(4)

文献[21]已经采用有限差分法并基于质量守恒定律以及式(3)和式(4)建立了详细的有限差分方程，也编写了相应的数值解算程序来计算瓦斯解吸扩散量，这里不再赘述。以此为参照，在本文的试验和模拟条件下来计算菲克扩散模型，并得到煤粒中的瓦斯解吸扩散的数值模拟数据。

2.2 游离瓦斯密度梯度驱动的新扩散模型

2.2.1 数学模型

菲克扩散模型主要考虑的是，煤粒瓦斯流动是由瓦斯含量的差异引起的，并没有区分开吸附态瓦斯和游离态瓦斯的赋存状态[21, 26]。像一些微孔中的吸附态瓦斯大部分情况下是处于相对静止的状态，实际上瓦斯流动过程的主要参与者是游离瓦斯(包含原始游离瓦斯以及表面解吸形成的游离瓦斯)。因此，参考菲克定律的假设，可以认为煤粒瓦斯扩散是由游离瓦斯密度梯度驱动的。基于传质的思想，考虑瓦斯质量流通量与游离瓦斯密度梯度成正比，具体数学方程为

Jm=-Dmgradρg

(5)

式中：Jm为煤粒中单位时间内通过单位面积的瓦斯质量，g/(cm2·s)；Dm为游离瓦斯的微孔道扩散系数，cm2/s；ρg为游离态瓦斯密度，g/cm3。

煤粒中的瓦斯含量用Langmuir方程[22]表示:

(6)

式中：a,b为朗格缪尔吸附常数，单位分别为cm3/g，1/MPa；ρa为煤的视密度，g/cm3；p为瓦斯压力，MPa；f为孔隙率；T0为标准情况下的温度，273.15 K；p0为标准状态下的压力，0.101 325 MPa；T为试验温度，K。

将煤粒中的游离瓦斯看作是理想气体[27]，则有

ρg=pM/R0T

(7)

式中：M为甲烷的摩尔质量，16 g/mol；R0为通用气体常数，8.314 J/(mol·K)。

假设煤粒为各向同性球形多孔介质，孔隙结构不受气体压力的影响，即不考虑吸附引起的煤体膨胀或解吸引起的煤体收缩[25]。瓦斯流动过程遵循质量守恒定律：

(8)

式中：ρs为瓦斯标准密度，7.17×10-4g/cm3；dr为沿球形煤粒半径方向的单元壳的厚度，m。

联立式(5)—式(8)可以推导出球形煤粒瓦斯解吸扩散流动的连续性方程：

(9)

瓦斯解吸流动方程的初始和边界条件为

(10)

式中:p0为解吸开始时的煤粒内部的初始瓦斯压力，MPa；pw为煤粒外表面的压力，MPa。

由于试验是在封闭空间内进行的，瓦斯随着解吸进程不断从煤粒扩散到外部自由空间，导致煤粒外表面的瓦斯压力逐渐增大。因此煤粒外表面的压力边界处于动态变化之中，表述为

(11)

式中：pw0为煤粒外表面的初始压力，试验设置的大气压，MPa；m为煤粒的质量，g；Vf为多样品管中自由空间的体积，cm3；Qm为t时刻单位质量煤粒的累计瓦斯解吸质量，g/g。

Qm的计算公式如下：

(12)

2.2.2 有限差分数值解算

在此使用有限差分的数值方法来对上述数学方程进行解算。首先将球形煤粒从球心至球面划分成N个节点，各节点间的距离是逐渐减小的，符合等比数列，如图5所示。以2个相邻节点(用实线表示)间的中心作同心球面(用虚线表示)。如此相邻2个虚线球面之间便形成球壳，在中心处形成1个实心球体。最终得到以0点为中心的实心球和包含各节点的N个球壳。

图5 球形煤粒节点划分

通过质量守恒定律可以推导出节点1到N-1的瓦斯流动差分方程：

(i=1,2,…，N-1;j=1,2,3，……)

(13)

(14)

式中：i,i-1,i+1为划分节点编号；j为时间节点编号；Δtj为第j个时间步长。

节点0处的差分方程为

(15)

(16)

节点N的边界方程为

(17)

其中,Qm(j-1)为第j-1时刻的单位质量煤粒累计解吸瓦斯质量，可由N节点和N-1节点的压力值的差计算：

(18)

由式子(13)—式(18)构成了第j时刻以N个节点瓦斯压力为未知量的完整差分方程组。文献[16, 21-22]已经由高斯迭代的思想开发了多个非线性方程组解算的程序代码，也介绍了相关的解算流程。在此基础上，对建立的差分方程组进行解算，具体解算步骤不再赘述。

试验获得的是单位质量煤粒解吸出来的瓦斯体积，为方便将模拟结果与试验数据进行比较，这里将模拟得到的单位质量煤粒解吸出来的瓦斯质量统一转化为瓦斯体积含量，则j时刻单位质量煤粒累计解吸的瓦斯体积Qtj为

Qtj=Qmj/ρs

(19)

数值解算中的参数选取见表2。其中a、b、ρa、f、Vf等均由试验手段测得，而Dm是在解算程序中不断调试反算而确定的。

表2 数值解算参数取值

3 结果与讨论

3.1 试验与解算结果的对比

将4种压力尺度下的瓦斯解吸试验数据与对应的密度新模型和菲克模型解算的模拟结果进行对比。以初始解吸压力为1 MPa为例进行说明，为更加直观地观察模拟结果与试验数据的匹配程度，这里将横坐标取为对数坐标进行展示，如图6所示。

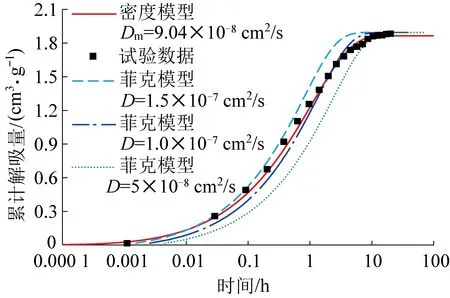
图6 2种模型的模拟曲线与试验数据的匹配(p0=1 MPa)

由图6可以看出，在试验的整个时间范围内，基于游离瓦斯密度梯度驱动的新扩散模型计算的解吸量随时间变化曲线与试验数据基本相符。有些试验点与模拟曲线存在些许偏差，但是从整个时间尺度来看，这些小误差是可以接受的。而菲克模型的计算结果只能在初始或者后期小时间段与试验保持一致，在整个时间尺度下的预测误差较大。总体来说，游离瓦斯密度梯度驱动的新扩散模型更精确，是可以用来描述煤粒中的解吸扩散流动过程的。另外从图6还能得出，菲克模型中的常扩散系数不能使试验数据与解算结果相吻合；而单独的常微孔道扩散系数值可使模拟结果与试验数据保持一致，并且不受时间的影响。

图7展现了不同初始解吸压力情况下的密度模型解算结果与试验数据的对比情况。由此可知，4种初始解吸压力下的模拟结果均与试验数据吻合良好，这进一步验证了密度模型的准确性。其中的关键参数-微孔道扩散系数Dm始终为9.04×10-8cm2/s，即不同初始解吸压力尺度下的微孔道扩散系数是相同的。虽然取了相同的Dm可能会导致有些试验点=与模拟曲线有轻微偏差，但从整体看这种误差是可忽略的，也表明了初始解吸压力对煤样的微孔道扩散系数影响不大。概括来说，密度模型的煤粒的微孔道扩散系数与时间、压力等状态参数无关。

图7 密度模型解算与试验数据的对比(Dm=9.04×10-8 cm2/s)

3.2 密度模型与菲克模型的讨论

近几十年有各种条件下的瓦斯扩散试验都被用来检验上述基于菲克扩散模型推导出的解析解、近似解以及数值解的准确性。但是通过大量的试验数据发现，经典菲克扩散模型的理论曲线与试验点之间存在较大的偏差，菲克模型的常扩散系数不能够精确表征整个试验时间尺度的瓦斯扩散过程。在特定的试验条件下，扩散系数必须随时间发生变化才能确保菲克模型的解算结果与试验数据相吻合。但是扩散系数随时间变化的原理及物理意义并没有得到很好的阐释。也就是说，目前没有强有力的证据能够表明煤粒的扩散系数是要随着某种特定的方程表达式而改变的。再一点就是，实际煤体中煤粒外部瓦斯压力随时间千变万化，一旦外界条件变化，扩散系数随时间变化的函数也将会发生变化，这也不方便实际应用。因此，一些动态扩散系数模型虽然能够保证与特定试验条件下的试验数据的吻合精度，也不能简单移植到复杂外界条件下的煤粒瓦斯解吸扩散的建模工作之中。尽管菲克定律模型简单，能够得到解析解，但无数的试验数据已证实了菲克定律的确不适用于煤粒中的瓦斯流动。

新密度扩散模型经由有限差分数值方法解算的结果，在整个试验解吸时间尺度能够很好地描述瓦斯的解吸扩散行为。并且其关键比例系数-微孔道扩散系数是一个常数值，与时间或者压力这种状态参数无关，只与煤的孔隙结构有关。除此之外，游离瓦斯密度梯度驱动的新扩散模型也具有较明确的物理意义，在表征瓦斯扩散特性方面比经典菲克模型更加精确合理。