离散双切换线性正系统的L1增益性能分析

席 敏，龙 飞

(1.贵州大学大数据与信息工程学院，贵州 贵阳 550025；2.贵州理工学院人工智能与电气工程系，贵州 贵阳 550003)

0 引言

离散时间切换正系统是一类特殊的混杂系统，由多个正子系统和控制子系统间切换次序的切换信号构成。切换信号可分为确定性切换信号和随机切换信号。正系统是初始条件和输入非负时，状态和输出也为非负的系统。正系统变量非负这一特性，广泛运用在生物学、经济学、网络通信、人口统计学、实际生产活动等系统建模中。例如，计算机网络协议传输控制系统、自动化切换电路系统[1-2]等。

对切换正系统进行稳定性分析时，不仅要保证整个系统稳定，还需考虑系统的正性。这增加了研究切换正系统的复杂度和难度。关于切换系统的稳定性的理论研究，形成了以Lyapunov函数、驻留时间(dwell-time,DT)、平均驻留时间(average dwell-time,ADT)、持续驻留时间(persistent dwell-time,PDT)和Co-positive Lyapunov函数等为主的分析方法。现有研究结果表明，相比传统线性Lapunov函数法，Co-positive Lyapunov函数法存在更低的保守性[3]。

切换正系统在运行时，不可避免地含有随机故障或不可控因素引起的系统动态参数变化。随机切换系统——马尔可夫跳变线性系统(Markov jump linear system,MJLS)常用来描述此类系统。MJLS是由随机切换信号(即Markov链)协调系统模态间切换的随机切换系统。对于MJLS的稳定性研究结论有均方稳定(mean-square,MS)、几乎处处稳定(exponential almost-sure stability,EAS)等。

由于混杂系统的复杂性，通过对切换系统的结构作变化，可将切换系统分为不同类型。本文中的切换正系统结构是受到确定性切换信号和随机切换信号的影响的离散时间双切换线性正系统(discrete-time dual-switched linear positive systems，DDSLPS)。

在DDSLPS中，子系统由多个不同的MJLS构成。每个MJLS子系统服从不同的Markov链。第一层切换由确定性切换信号γk控制MJLS子系统间的切换。第二层切换由各MJLS的Markov链σk控制系统模态间的切换。在Markov子系统间发生切换时，各Markov系统模态也在同时发生切换。相比一般切换正系统只有一个切换信号来控制系统运行，例如MJLS由Markov链控制系统模态间的切换，DDSLPS必须考虑确定性切换信号与随机切换信号对整个系统的影响，以及系统的正性。因此，DDSLPS的稳定性分析和镇定分析比普通切换系统更加复杂。

对于离散时间切换系统而言，其采样周期受到时滞的影响。时滞可以是系统中控制器的计算延迟，也可以是控制器和监控器的通信延迟等。这些未知的、时变的、有界的时滞，称为系统中存在的指数参数不确定性。有学者在文献[4]中提出了含有指数不确定性的连续时间线性系统的鲁棒镇定问题,将指数不确定性转换为一个服从加性模有界不确定性的混杂多面体模型。受到此方法的影响，本文将含有指数不确定的DDSLPS转换为模有界不确定性的系统进行研究。

系统性能不仅受到内部参数改变和时滞带来的影响，也容易受到外部扰动的影响。为了衡量切换正系统的抗干扰能力，通常用L1增益性能来评估系统干扰抑制水平性能。L1增益系数越小,系统的干扰抑制水平越高。所以对切换正系统的抗干扰性能分析引起了广泛的关注。文献[5]研究了切换正系统L1增益性能分析对实际生产系统中的应用，利用Co-positive Lyapunov函数方法,研究了在驻留时间限制下存在时延的离散时间切换正系统的指数稳定性以及L1增益性能，并得到时延对系统L1增益性能的影响。文献[6]利用线性编程(linear programming,LP)对离散时间正MJLS进行L1增益分析并进行正滤波器设计。利用线性Lyapunov函数构建一个“等价”的确定离散时间线性系统，给出的充分条件能保证系统随机稳定并有L1增益性能。

本文在以上研究的基础上，将切换正系统以及离散时间正MJLS对L1增益性能的研究方法应用到DDSLPS中。针对存在指数不确定性的DDSLPS,通过结合Co-positive Lyapunov能量衰减函数、MJLS的暂态分析、PDT等主要理论方法,证明DDSLPS在扰动为零时鲁棒-几乎处处稳定(Ronust-exponential almost-sure stability,Ronust-EAS),并将此证明方法推广应用于系统L1增益性能分析中。仿真分析充分验证了结论的正确性。

1 问题描述

本文考虑如下的DDSLPS：

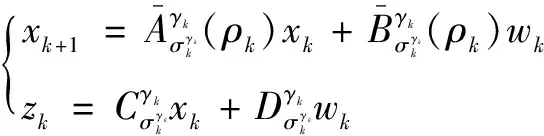
(1)

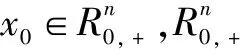
定义1 系统(1)对于所有的x0≥0、wk≥0;对于k∈N,都有x0≥0、zk≥0。

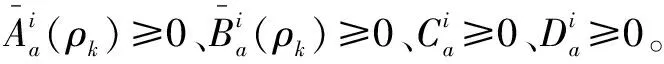
注1 为了便于稳定性分析,将利用指数不确定性的相关引理，把具有指数不确定性的双切换离散时间线性系统表示为具有附加范数有界不确定性的双切换离散时间线性多面体系统。

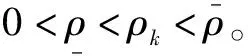
L(ρ)=L0+L1ρ+L2ρ2+…+Lhρh

(2)

所以能找到一个具有(h+1)个顶点的凸组合L(ρ),使得：

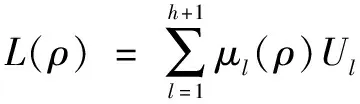
(3)

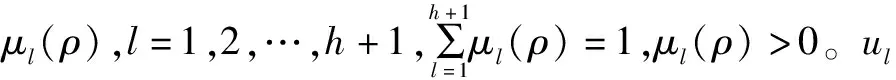
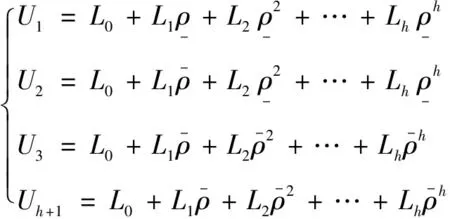
(4)

不确定参数ρ和μl(ρ)的关系如下：

(5)

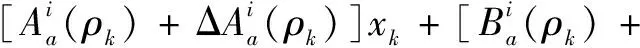
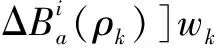
(6)

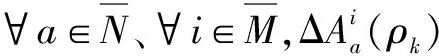
式中：sup表示最小上确界。

注2 综上可知,具有指数不确定性的双切换离散时间线性系统已经表示为具有附加范数有界不确定性的双切换离散时间线性多面体系统,如式(6)所示。系统模型(1)中同时包括了具有多项式的不确定性的双切换离散时间线性系统和具有范数有界不确定性的双切换离散时间线性系统。因此,系统(1)可以用于对具有复杂切换特性的系统建模。

注3 为了研究确定性切换系统的稳定性，接下来将阐述持续驻留时间PDT 方法。

定义2[9]考虑切换时刻k0,k1,...,kn。其中,k0=0。假如存在无数个长度大于τ的不相交区间,且具有该性质的连续区间被一个不大于T的时间间隔分割,则常数τ被称为PDT、T被称为持续周期。

注4 PDT由切换规则相同的阶段构成。每个阶段均包括τ和T这两部分。在τ部分中,只有一个任意的子系统激活并且作用时间至少为τ。在T部分中,有多个子系统激活。每个子系统的作用时间小于τ且所有子系统的激活总时间小于T。

DDSLPS结构如图1所示。

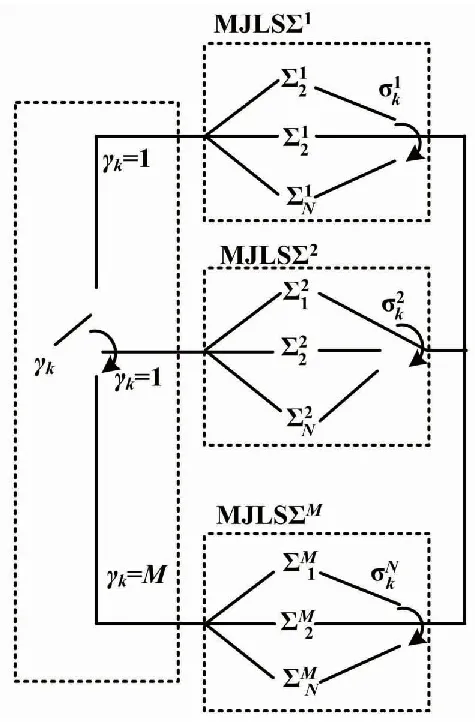
图1 DDSLPS结构图

DDSLPS的切换序列如图2所示。

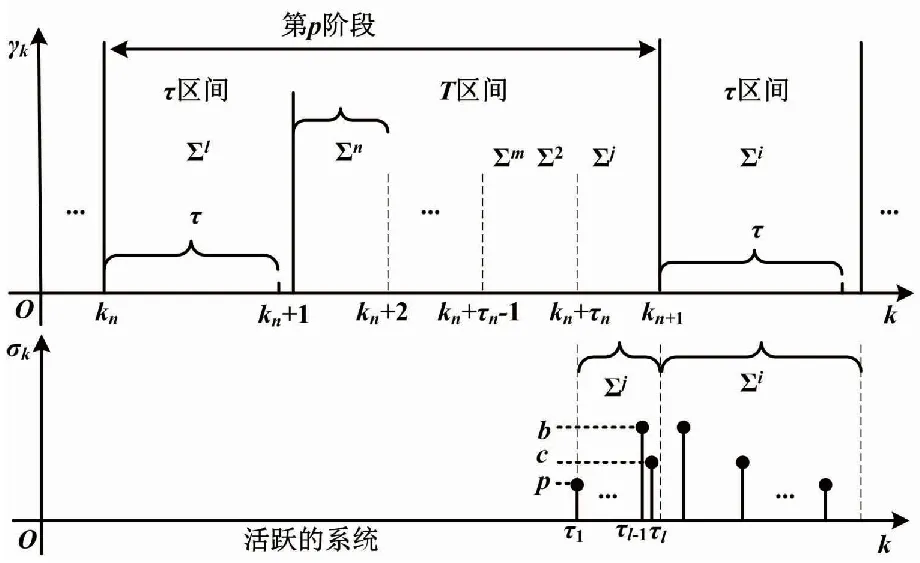
图2 DDSLPS PDT切换序列

{kn,kn+1,…,kn+τn-1}表示确定性切换信号γk在区间[kn,kn+1)的切换时刻。{τ1,τ2,…,τl}表示随机切换信号σk在[τ1,τl)的切换时刻。(kn+1)表示第p个阶段中时刻kn的下一个切换时刻。kn+1表示第(p+1)个阶段的切入时刻。

(7)

等价于：

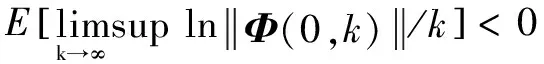
(8)

式中：Φ(0,k)为系统(1)的随机转移矩阵。

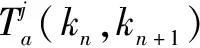
则在初始概率分布F=[f1,f2…fN]已知时，有以下等式成立：

(9)

(10)

定义4 当常数x>0, 若系统(1)满足以下两个条件。

①任意初始条件下,当没有外部扰动的时候,系统是鲁棒EAS稳定的。

②在零初始条件下,对于所有非零干扰wk都满足所有的可容许不确定性下,有：

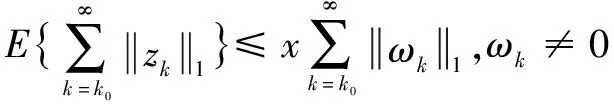
(11)

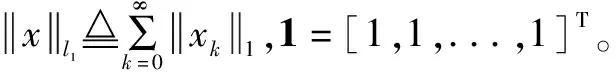
注5 对于DDSLPS而言，由于数量之和对于正系统更可取,使用向量的1范数定义的L1增益更适合于评估性能。x为外部扰动抑制度。x越小，表明系统抵御外界干扰的能力越强。

2 主要结果

2.1 Robust-EAS稳定性

当系统中扰动输入为零时，系统(1)可以表示为:

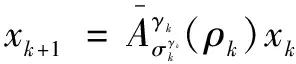
(12)

接下来，给出系统(12)Robust-EAS稳定的充分条件。

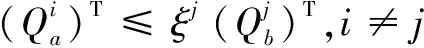
(13)

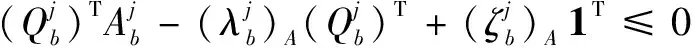
(14)

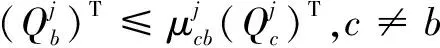
(15)

(16)

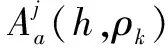
此处：

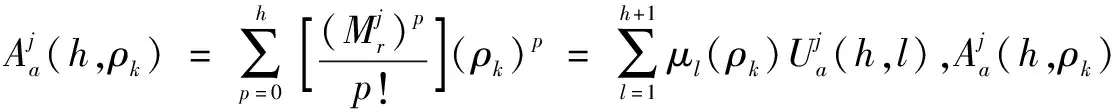
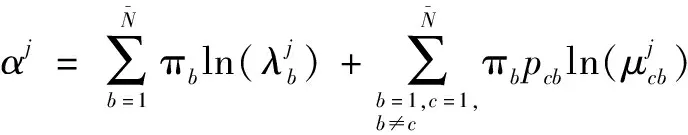
(17)

(18)

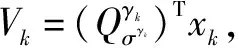
(19)

(20)

在区间[τl,kn+1)上，只有随机切换系统b模态在作用。由条件式(14)、条件(15)以及重复步骤(17)、步骤(18)，可以得到:

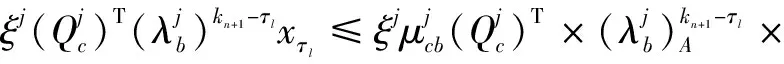
(21)

从条件(9)、条件(10)可以得到:

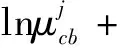
由αj、βj的等式可以得到：

E{lnVkn+1}=βj+αjΔk+E{lnVτ1}

(22)

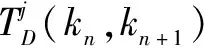
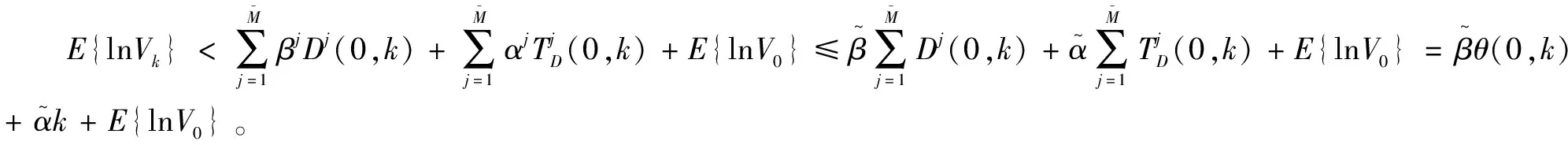
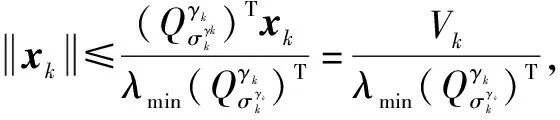
由此，即可证明系统(1)在wk=0 是鲁棒EAS稳定的。

2.2 L1增益性能

(23)

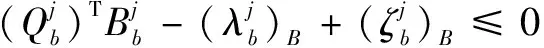
(24)

(25)

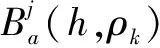
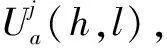
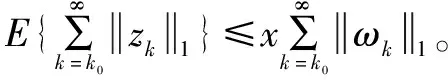
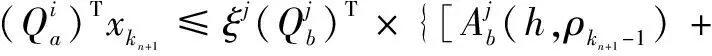
(26)

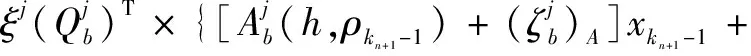
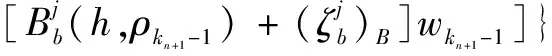
(27)

由条件(14)、条件(15)、条件(24)，得出:

(28)

由式(28)可以得到：

(29)

接下来，按照之前证明wk=0 的步骤，可以得到系统在wk≠0 系统(1)E{Vk}<0。令：

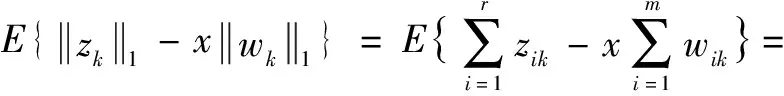
(30)

由式(30)以及条件(23)、条件(25)，可得：

(31)

证明出DDSLPS具有L1增益性能。

3 数值仿真

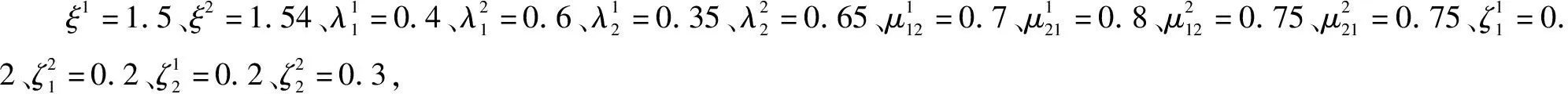
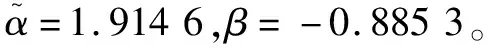
根据条件(18)，系统(1)要保证鲁棒EAS稳定，那么PDT的限制为T<0.860 1τ-1.86。选取T=12、τ=22，并选择以下的PDT限制的周期确定切换信号γk。

式中：n=0,1,2,…；M为确定性切换信号的周期，M=35。

确定性切换信号γk如图3所示。图3中：1阶段的M为0；2阶段的M为1。

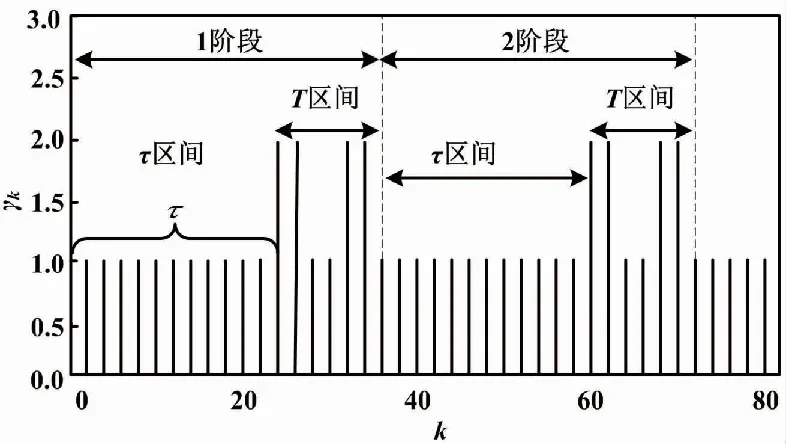
图3 γk信号示意图

图4为系统(1)在w=0、初始条件为x0=[0.6 1]T时的 7次样本实现。显然，系统(1)是鲁棒EAS稳定的。

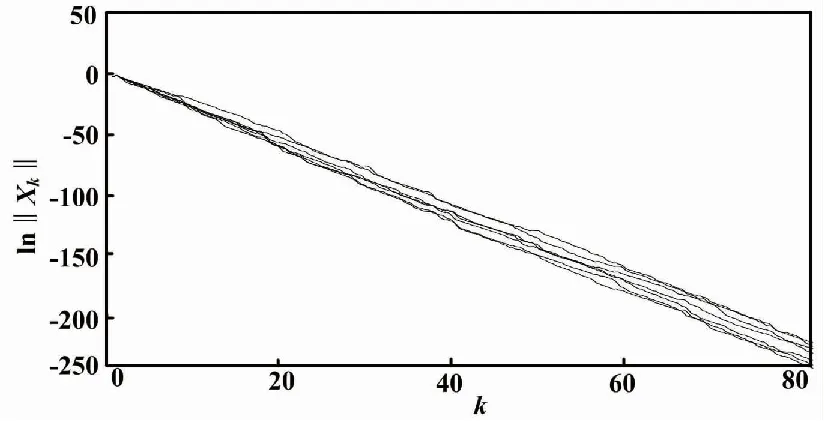
图的7次样本实现(w =0)

为考虑扰动抑制性能，外部扰动wk设置为方波信号：

方波信号如图5所示。

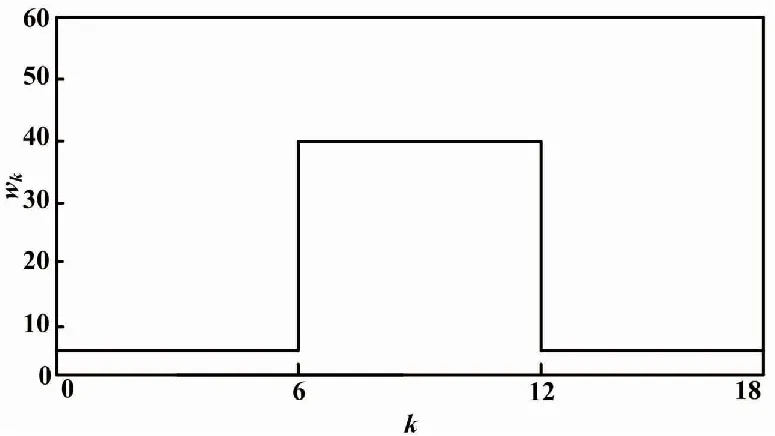
Fig.5 wk信号示意图

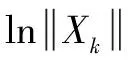
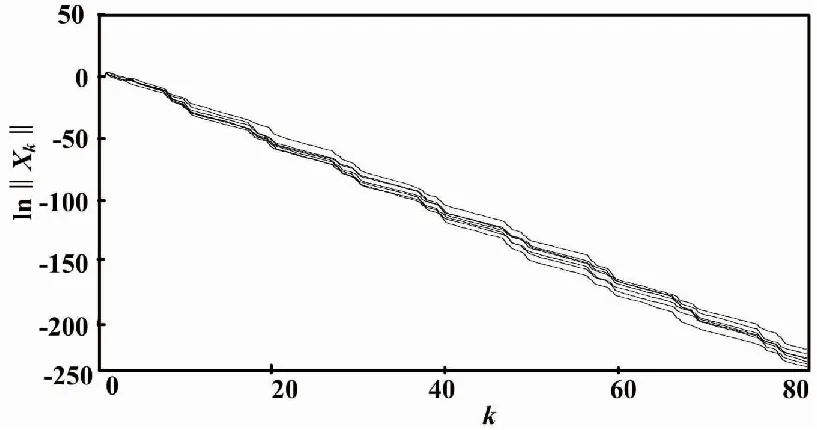
的7次样本实现(wk ≠0)

4 结论

鲁棒稳定以及扰动抑制问题是研究混杂系统稳定性的重要问题。本文对含有指数不确定性的DDSLPS的L1增益性能进行了研究。首先，将指数不确定性转换为附加范数有界不确定性。然后，利用PDT方法限制确定性切换信号，并基于正系统的理论中的Co-positive Lyapunov能量衰减函数法以及MJLS暂态分析理论，给出了保证DDSLPS Robust-EAS稳定的充分条件，并将此方法推广得到DDSLPS满足L1增益性能指标x的充分条件中。最后，得到DDSLPS不仅满足Robust-EAS且系统具有L1增益性能的充分条件。该条件利用Matlab的LP得出,减少了计算复杂度。仿真算例充分证明了结论的正确性。