移相控制的LLC 变换器轻载增益研究

2022-02-25袁义生张钟艺兰梦罗

电源学报 2022年1期

袁义生，张钟艺，兰梦罗

（华东交通大学电气与自动化工程学院，南昌 330013）

LLC 谐振变换器具有软开关、功率密度高、电磁干扰EMI（electromagnetic interference）较低等优点，且输入输出电压可调范围大，能够作为应对负载功率变化大的直流供电电源。因此如何实现全负载范围内的高效率工作成为了当今LLC 谐振变换器研究领域的重点，而要使得效率提高，就必须实现全负载下的零电压开关ZVS（zero-voltage switching）与零电流开关ZCS（zero-current switching）。实现这一目标的难点之一就是实现轻载情况下的ZVS 死区时间设计。

轻载时，LLC 谐振变换器一般工作在高频段，增益小于1。近年来，针对半桥LLC 谐振变换器[1-4]实现轻载ZVS 采用一种新颖的非对称脉宽调制APWM（asymmetrical pulse width modulation）控制方式[5-7]，通过使桥臂开关管在一个周期内按照非对称的占空比互补导通，使得各管死区时间内的谐振电流能够依据负载的变化而变化，从而满足各管实现ZVS 的条件，但会造成副变整流桥臂电流不平衡，加大了功率损耗计算难度，且直流增益求解比较复杂。而全桥LLC 谐振变换器实现轻载ZVS 的研究，首先要区分控制方式，传统的LLC 谐振变换器采用变频控制方式[8-12]，在重载低频工况时是比较有效的，开关管均可实现ZVS，整流桥二极管均可实现ZCS，直流变换效率高。但在轻载高频工况时，整流桥二极管无法实现ZCS，且开关频率的增益调节范围大大缩小，变换器工作频率波动大，增加了额外的损耗。因此，为克服上述问题，可采用变频移相控制方式。

采用变频移相控制的LLC 谐振变换器[13-16]电路分析一般采用时域分析法，能够比较准确地描述各个电气量之间的关系。在时域分析法的基础上发展出了工作模态法[17-18]，工作模态法中模态的建立是基于特定频率下对电路工作波形进行理想化处理后，归纳总结规律，其电路分析结果不具备普遍适用性。文献[19-20]详细分析了在高频轻载情况下寄生电容对电路工作波形的影响。

上述的半桥或是全桥LLC 谐振变换器，采用了一些不同的控制方式来实现轻载ZVS。但是均未对死区时间内的谐振电流进行分析，均忽略死区时间对占空比及轻载增益的影响，利用开关管关断时刻的谐振电流大小是否满足开关管寄生电容充放电过程中电荷守恒，来作为实现ZVS 的死区时间设计依据，必然会造成死区时间设计过大，降低了变换器工作效率。

本文通过时域分析法，详细分析采用变频移相控制策略的全桥LLC 谐振变换器在轻载情况下增益变化情况。梳理明确谐振电流在能量传输、超前臂与滞后臂死区等阶段的电路工作波形。考虑寄生电容对谐振电流的影响，通过对电路工作波形进行优化处理，形成3 个假设条件，建立寄生电容与死区谐振电流的电荷守恒的等式关系，建立谐振电流与励磁电流在死区临界结束时刻的等式关系，建立增益与死区大小及移相占空比的等式关系。通过上述等式关系，又推导出增益G 受移相占空比D、死区时间Td以及开关频率fs等参数的影响函数关系，从而找到既满足ZVS 也满足增益要求的最优移相占空比和死区时间大小。

1 移相控制LLC 谐振变换器

1.1 电路结构

图1 为LLC 谐振变换器拓扑电路结构，其由H桥臂开关管Q1—Q4（Q1、Q3构成超前臂，Q2、Q4构成滞后臂）、谐振单元LrCr、主变压器TX1（励磁电感Lm）、整流桥D5—D8及输出滤波电容Co构成。其中D1—D4为开关管Q1—Q4的体二极管，Coss1—Coss4为开关管Q1—Q4的寄生电容。

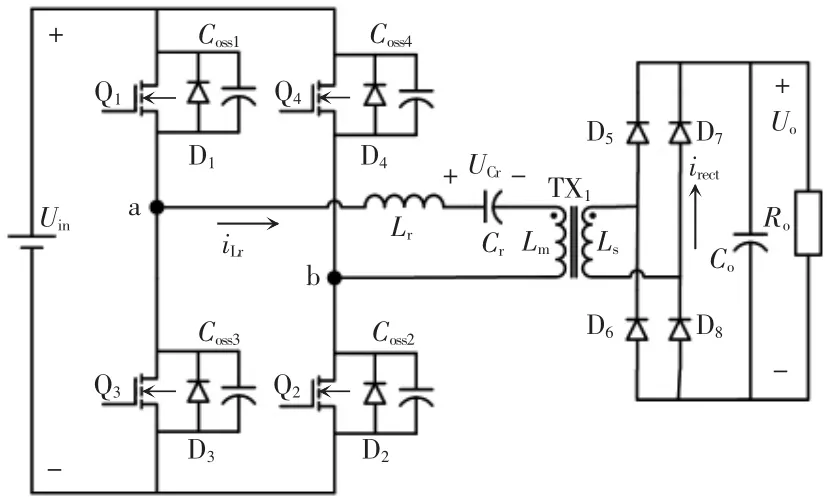
图1 电路结构Fig.1 Circuit structure

1.2 变频移相控制驱动

轻载工况下，LLC 变频移相控制驱动波形及电路工作波形如图2 所示。

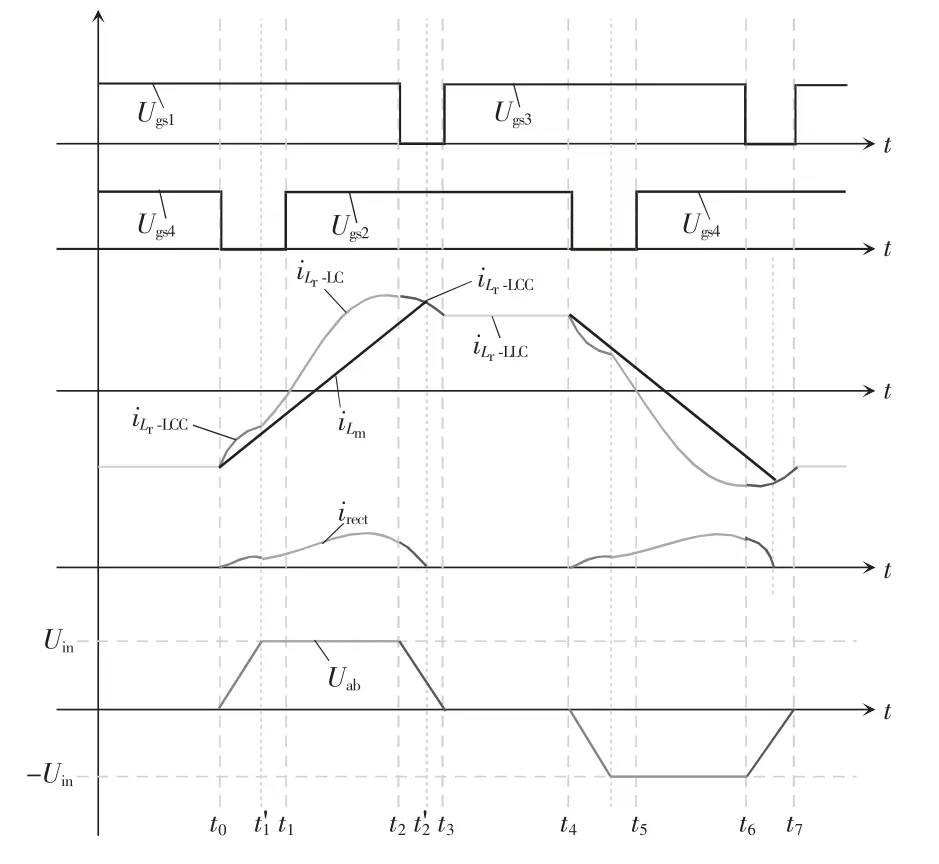
图2 电路工作波形Fig.2 Working waveforms of circuit

图2 显示出了暂态分析的各个阶段，其中：①t0～，滞后臂死区Lr、Cr、Coss谐振（LCC 谐振）阶段；②～t2，Lr、Cr谐振（LC 谐振）阶段；③t2～，超前臂死区Lr、Cr、Coss谐振（LCC 谐振）阶段；④～t3，谐振电流与励磁电流相等，开启了Lr、Lm、Cr三元器件谐振（LLC 谐振）过渡阶段；⑤t3～t4，谐振腔输入电压为0，进入LLC 谐振环流阶段。不同阶段的谐振电流将采用iLr-x的格式进行标识，其中x 表示阶段缩写。

2 电路分析

2.1 设立假设条件

按照传统的分析方法，进入死区时间极短，谐振电流基本不变的优化处理，导致只须求解出超前臂与滞后臂开关管关断时刻的谐振电流，即可表示整个死区过程中的谐振电流，并用来分析判断实现ZVS 所需要的能量是否足够超前臂与滞后臂在死区内完成寄生电容充放电过程。结合图2 发现，轻载工况下这种优化处理所造成的误差是巨大的。超前臂与滞后臂开关管关断电流均比较小，在2 个死区内，谐振电流也在不断衰减，按照传统方法计算出的死区时间明显偏小，谐振电流带电荷量不足以使得开关管寄生电容完全充放电，导致无法实现ZVS。如果盲目地在所计算出的死区时间上加上裕度，可能会造成过大的死区裕度，寄生电容电压降至0 后反弹，ZVS 无法实现，增加开关管导通损耗，并且死区过大，对电路增益分析所造成的误差也会越大。

因此轻载工况下实现ZVS，必须对死区时间内谐振电感Lr，谐振电容Cr与开关管寄生电容Coss之间的谐振过程进行分析。基于图2 的电路工作波形，可知滞后臂死区t0～t1之间谐振电流的大小是略小于励磁电流的，在超前臂死区t2～t3之间谐振电流会对寄生电容Coss充电，导致电流下降，副边整流电流irect在t0～内使整流二极管导通，造成励磁电感Lm被输出电压Uo箝位，励磁电流iLm保持相同斜率上升。此消彼长，谐振电流就有可能等于励磁电流，从而结束励磁电感Lm的箝位，进入LLC 谐振阶段，继续给Coss充电，实现ZVS，使电流下折。

借鉴传统分析方法中的优化处理思想，忽略LLC 谐振过渡阶段～t3，对电路工作波形进行优化处理，建立几个假设条件：①在超前臂死区结束的时刻即t3，谐振电流（t3）等于励磁电流（t3）；②超前臂死区实现临界ZVS，并且滞后臂死区的谐振电流近似等于励磁电流，但并不影响励磁电感Lm被输出电压Uo箝位；③滞后臂死区时间与超前臂死区时间相当，这样死区时间就可以作为一个未知变量Td。当精确求出超前臂死区大小之后，滞后臂死区大小只须在此基础上增加一定裕量。在上述假设条件基础上，可使得励磁电流在半个开关周期内具有对称性，简化了求解关键时刻励磁电流的计算。

经过优化处理后的工作波形如图3 所示。

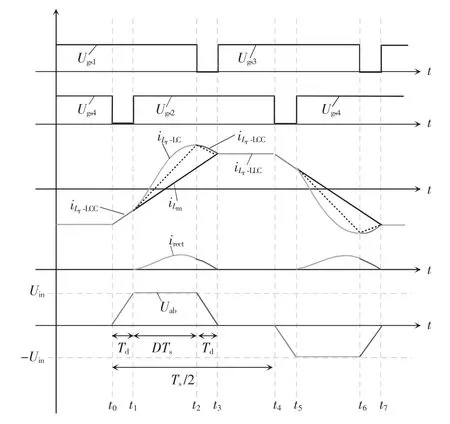
图3 优化处理电路工作波形Fig.3 Working waveforms of circuit with optimal processing

2.2 各阶段时域分析

各阶段建立复频域等效电路，如图4 所示。

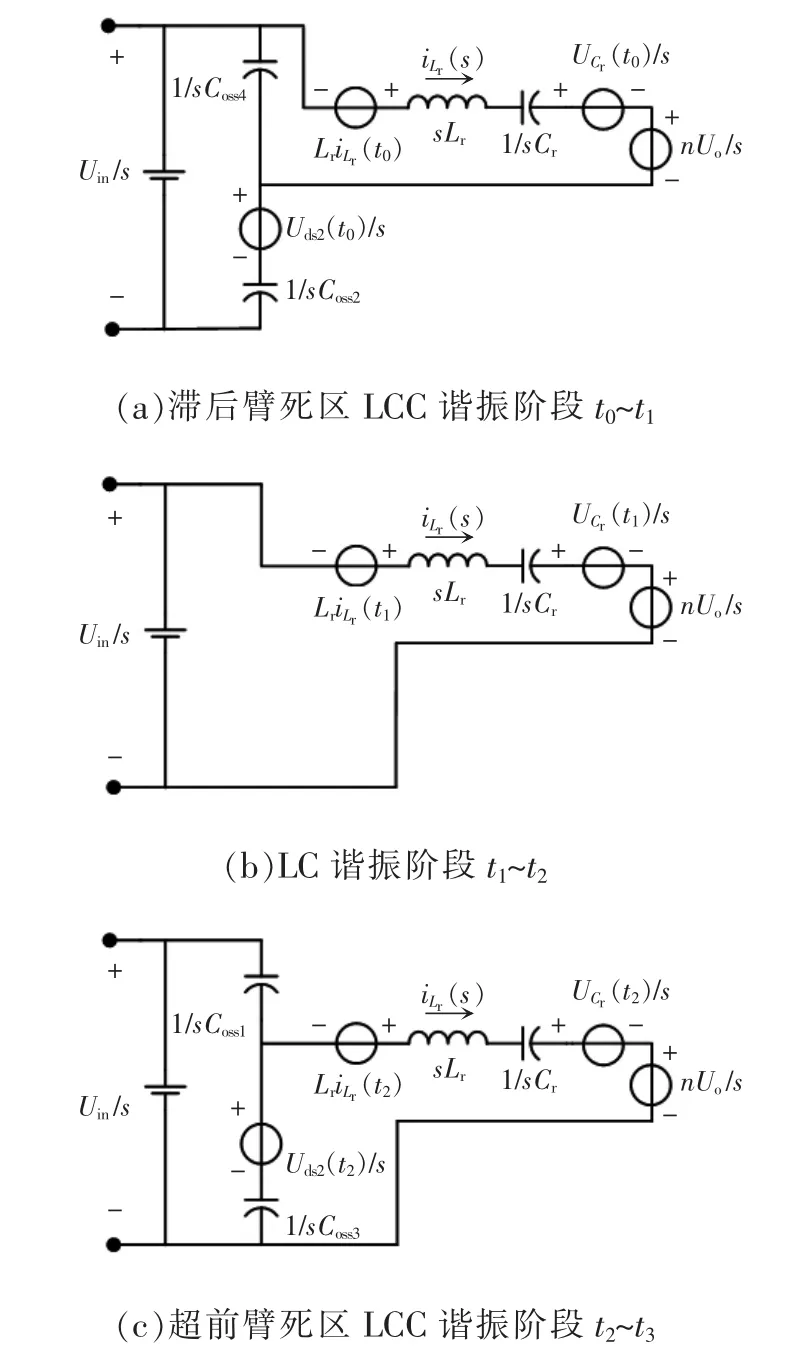
图4 等效电路Fig.4 Equivalent circuits

由于LLC 谐振阶段t3～t4为谐振环流阶段，为简化分析，认为谐振电流幅值不变，建立复频域等效电路意义不大。

通过对各阶段复频域等效电路列网孔电流方程，可得出对应阶段谐振电流s 域表达式，进而得出时域表达式。

（1）滞后臂死区LCC 谐振阶段t0～t1，电路方程为

（2）LC 谐振阶段t1～t2，电路方程为

（3）超前臂死区LCC 谐振阶段t2～t3，电路方程为

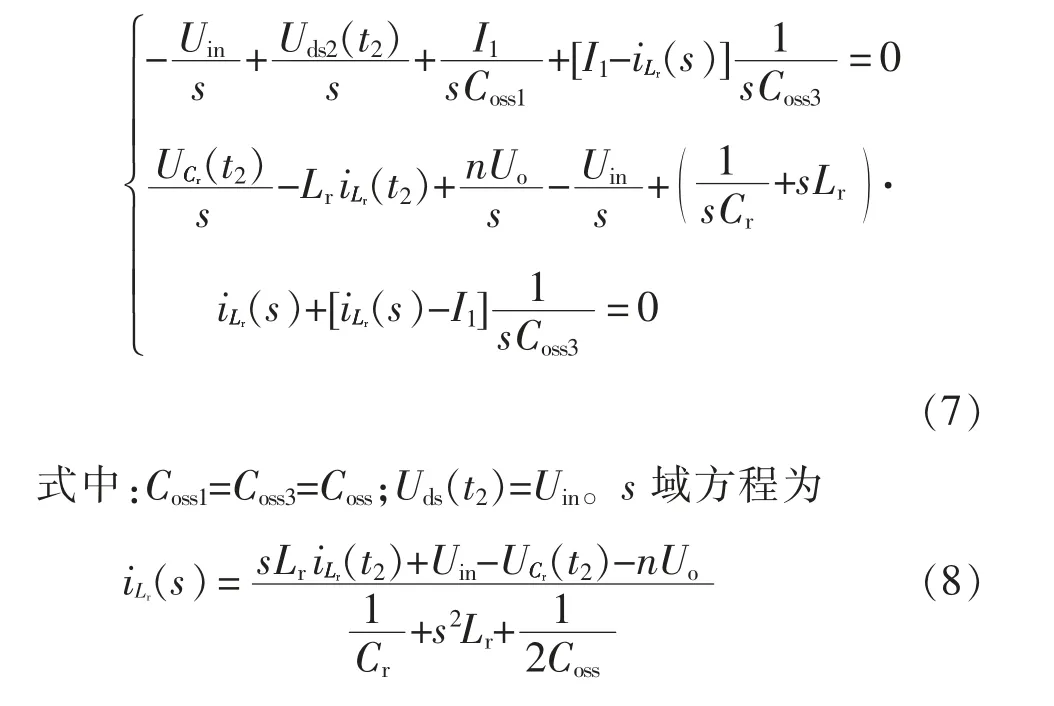
时域方程为

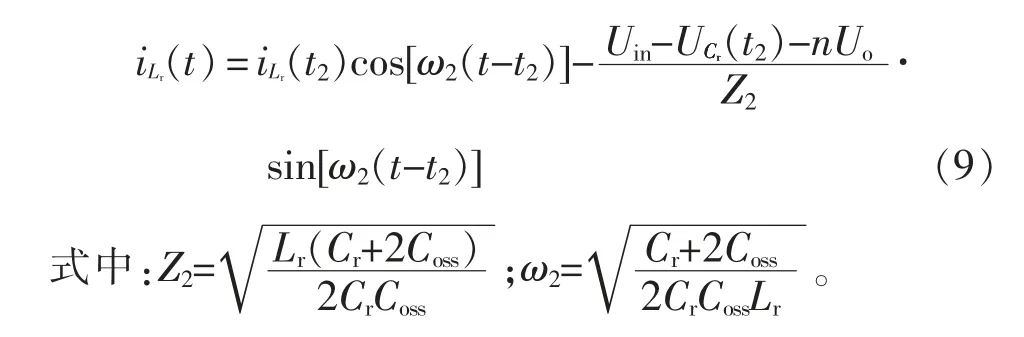
3 增益公式及约束关系

根据设立的假设条件，结合时域分析法，可建立以移相占空比D、死区时间Td和增益G 作为未知量，开关周期Ts、寄生电容Coss、主变压器变比n、输入电压Uin以及谐振腔参数Lm、Lr、Cr作为已知量的等式关系。

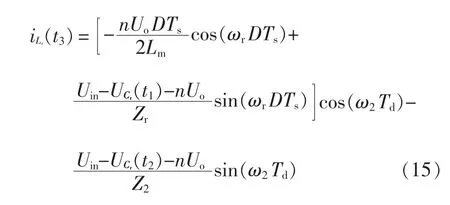
结合式（11），假设条件1 得等式方程为

在对电流积分计算中，LC 谐振阶段的谐振电流iLr-LC（t）与超前臂死区LCC 谐振阶段的谐振电流iLr-LCC（t）线性化处理，环流阶段t3～t4的谐振电流iLr-LLC（t）衰减量比较小，看做恒流，即。那么最终的电流积分表达式为

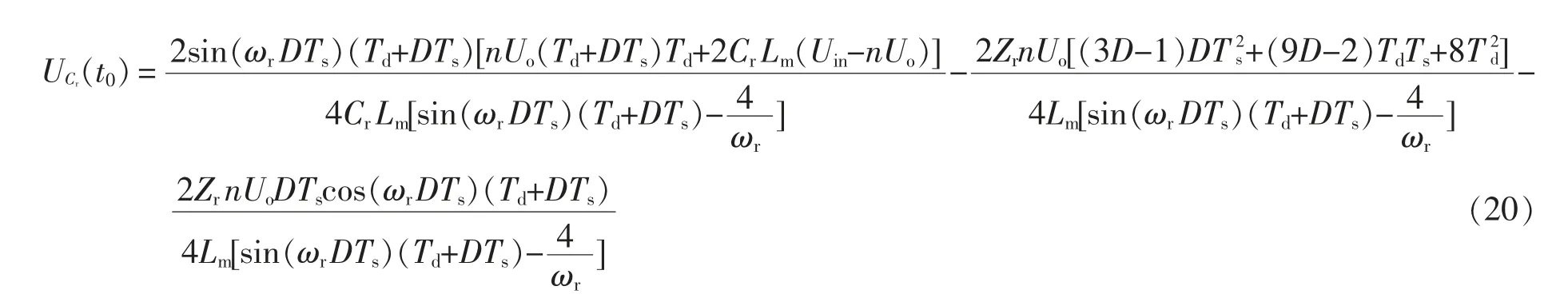
进而求出UCr（t2）表达式为

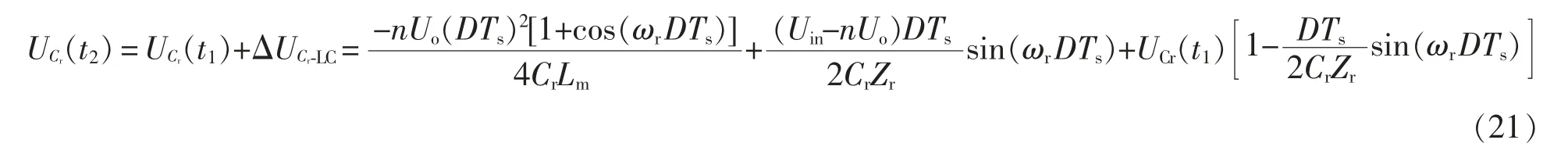
基于假设条件2，可根据电荷守恒，列出等式方程

依据假设条件所设立的等式方程式（16）、式（22），通过消去未知变量nUo，形成隐函数等式，再把电气参数即式（13）、式（19）、式（20）及式（21）代入，可求出直流增益G 为

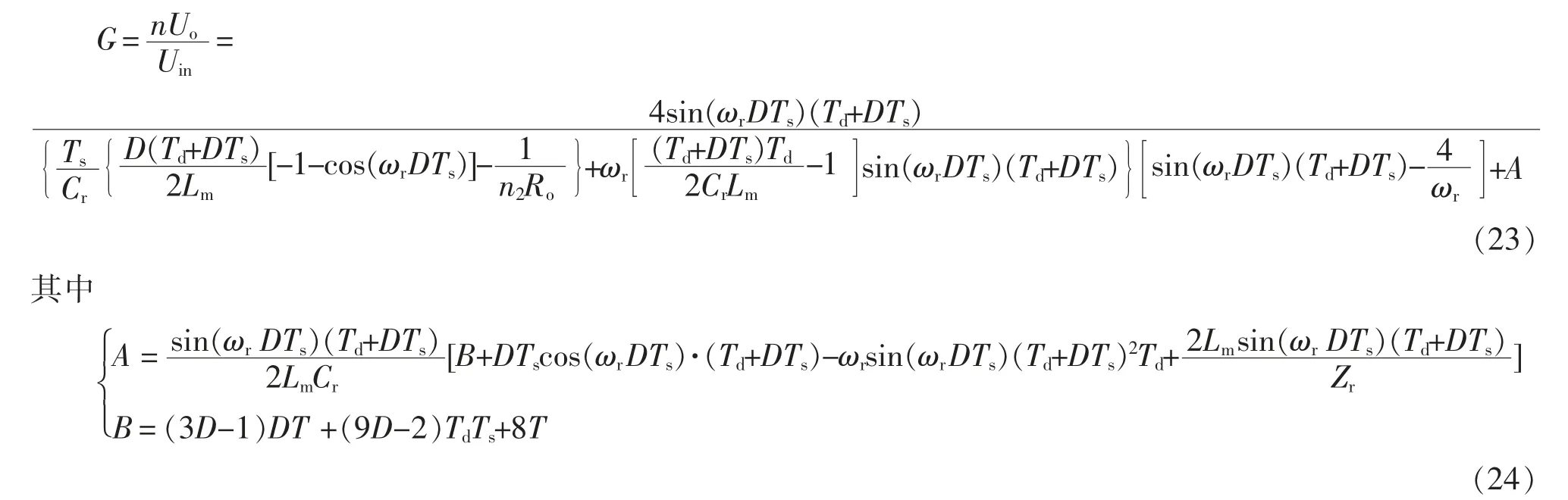
根据式（23）也能看出，变频移相控制模式的LLC 谐振变换器的电路分析与传统变频控制LLC的电路分析有所不同，增益G 的表达式与移相占空比D 与死区时间Td这2 个未知量有关，而传统的变频移相控制电路分析是忽略死区的，因此得到增益G 的表达式是不含Td的，但是轻载情况，Td的变化所造成的的影响是不可以被忽略的。因此，本文所得出的增益G 的表达式更加准确。

4 实验设计

4.1 样机设计

样机设计参数如表1 所示。

表1 样机设计参数Tab.1 Parameters for prototype design

样机额定输出电阻为Ro-R=48.4 Ω，额定功率为PR=U/Ro-R=529 W，取5%的轻载，即样机实验输出电阻取Ro-L=968 Ω，已知LLC 谐振变换器，开关管耐压Uds=Uin=200 V，经过查阅Datasheet，可知IPW60R 070C6 型MOSFET 管在Uds为200 V 时，寄生电容Coss为130 pF，本文样机设计寄生电容为450 pF，因此在开关管源极与漏极之间并联320 pF 的独石电容。上述样机参数代入到式（23）中，并设置计算区间，如表2 所示。

表2 计算区间参数Tab.2 Calculation of parameter ranges

可得出增益G 与死区时间Td，移相占空比D 函数关系的G=f1（Td，D）三维图像，如图5 所示。

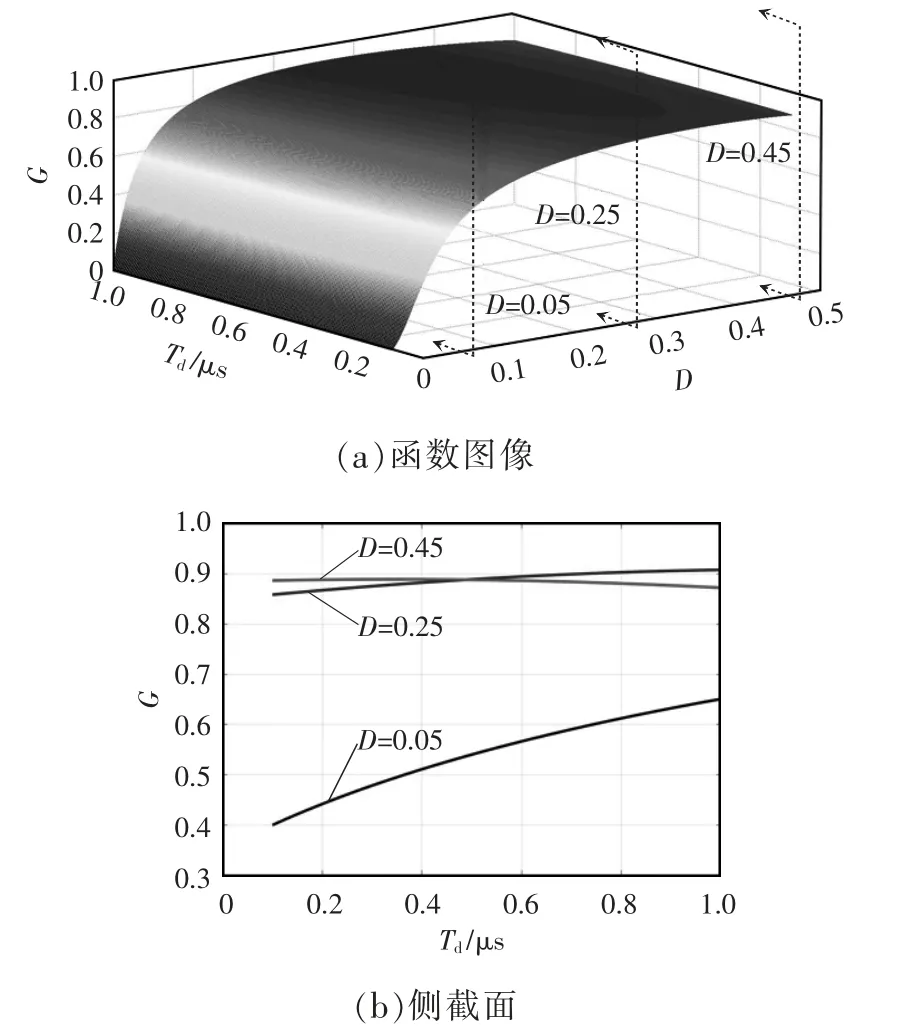
图5 函数G=f1（Td，D）三维图像Fig.5 Three-dimensional image of function G=f1（Td，D）

从图5（a）中可明显看出，随着移相占空比D 的增大，输出增益也增大。从图5（b）中可明显看出，固定移相占空比D，随着死区时间Td的增大，输出增益也缓慢增大，但随着D 增大，死区时间Td对输出增益的影响能力将越来越小，说明了死区时间确实会影响轻载工况下LLC 谐振变换器的增益。

同时，依旧代入上述样机参数及计算区间于假设条件2 所推式（22），得到实现临界ZVS 的约束关系隐函数f2（Td，D）=0，通过Matlab 作出相应的隐函数曲线。根据表1，给定输出增益要求G=0.8，结合图5，作出相应的横截曲线f1（Td，D）=0.8，如图6 所示。

从图6 中可知，两曲线交点对应的死区时间Td1与最优移相占空比D1既能够实现临界ZVS，又能满足给定增益要求。

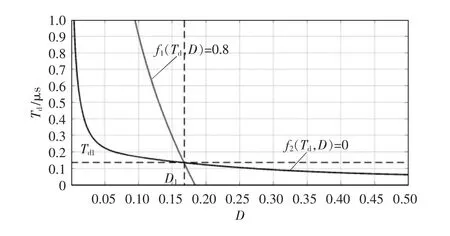
图6 最优占空比选取Fig.6 Selection of optimal duty ratio

4.2 仿真实验

根据图6，取D1=0.17，超前臂死区时间Td1=150 ns，滞后臂死区时间Td2=200 ns，根据样机设计参数，进行Saber 仿真。仿真结果如图7 所示。

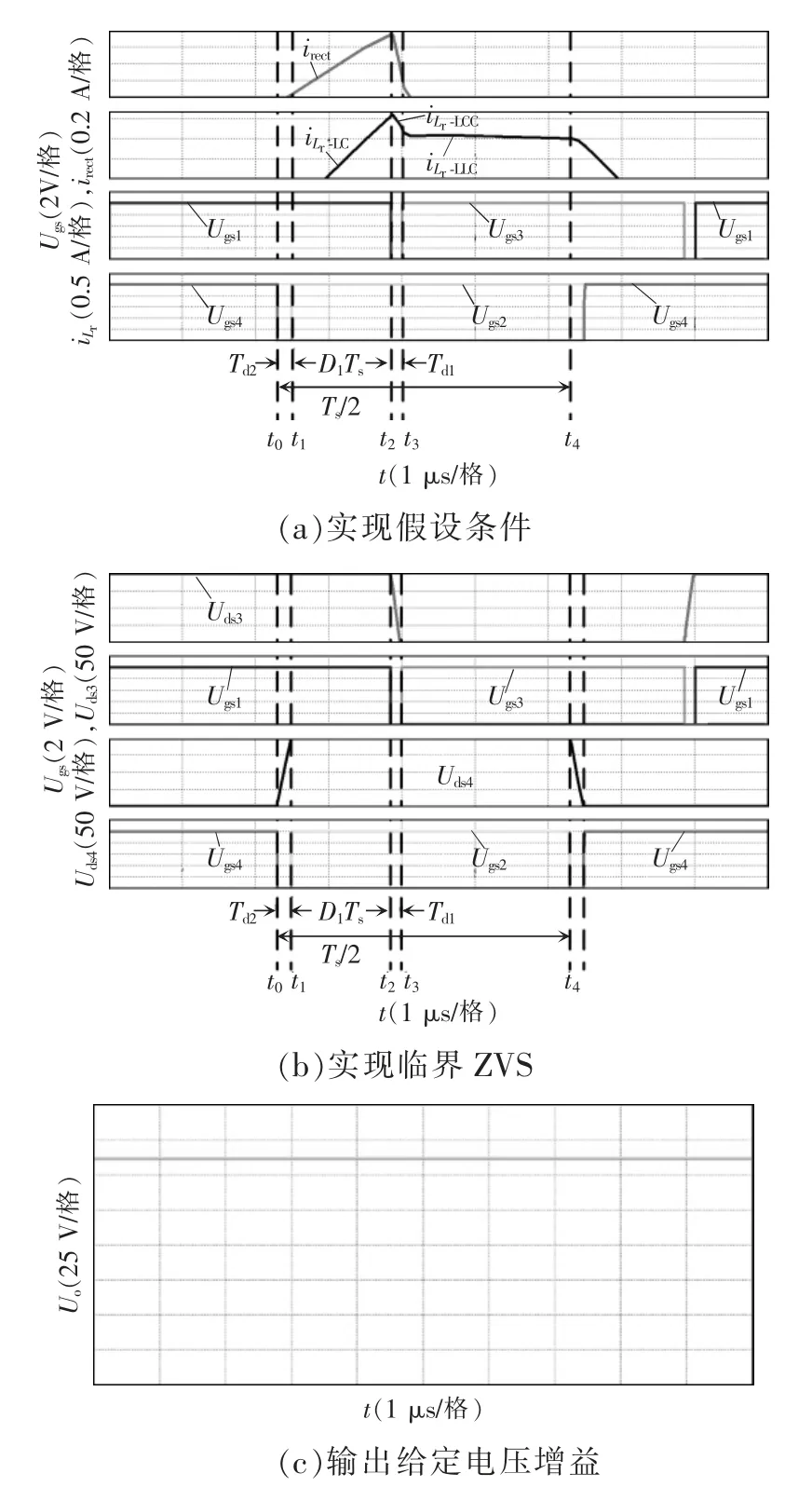
图7 仿真结果Fig.7 Simulation results

由于在仿真中，励磁电感与谐振电感相当于串联，因此励磁电流无法测量，为了验证假设条件1的实现，可通过测量整流桥电流irect来判定，已知，从图7（a）中可得，在t3时刻，irect≈0。谐振电流的工作波形也与图4 一致。从图7（b）中可得，超前臂与滞后臂死区时间能够实现临界ZVS。从图7（c）中可得，输出电压Uo=（160±5）V，与给定增益要求基本一致。

4.3 样机实验

样机实体照片如图8 所示。

图8 实验样机Fig.8 Experimental prototype

为了保证样机死区时间内能够实现ZVS，实现给定增益要求，样机超前臂死区时间Td3与滞后臂死区时间Td4均会在仿真实验临界ZVS 死区时间Td1基础上有所提高。实验结果如图9 所示。

由图9（a）中可看出，开关周期Ts=8 μs，驱动时序满足要求，移相时间D2Ts=1.4 μs，近似等于仿真实验中移相时间D1Ts=1.36 μs，从谐振电流i 的趋势来看，也与仿真实验结果几乎一致。

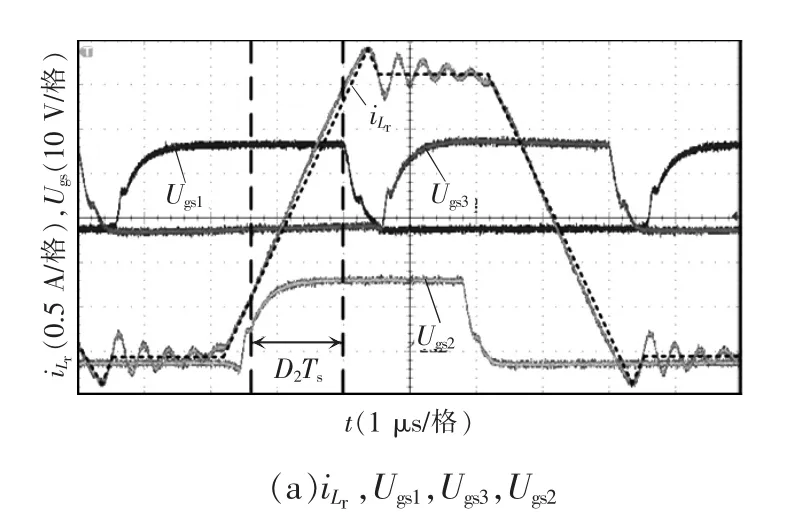
图9 实验结果Fig.9 Experimental results

所采用的的驱动电路经测试，开关管驱动电压截断下降时间为tf=400 ns，图9（b）中Ugs1下降起始到Ugs3上升起始之间的时间tgs=560 ns，那么超前臂死区时间Td3=tgs-tf=160 ns，图9（c）中驱动电压Ugs2下降起始到驱动电压Ugs4上升起始之间的时间tgs=640 ns，那么滞后臂死区时间Td4=tgs-tf=240 ns，均与仿真实验设计几乎一致。对比图9（b）与图9（c），可以发现超前臂死区时间内谐振电流明显比滞后臂死区时间内谐振电流大。图9（d）中超前臂开关管Q3实现了临界ZVS，当Uds3快降为0，Ugs3开始上升。图9（e）中滞后臂开关管Q4实现了临界ZVS，当Uds4快降为0，Ugs4开始上升。也与仿真实验结果基本一致。图9（f）中输出电压Uo达到了给定输出增益要求的160 V，输出电流平均值io-ave=170 mA，约等于Uo/Ro-L=160 V/968 Ω=165 mA，证明设计的样机实验验证了本文对移相控制的LLC 变换器轻载增益研究的有效性。