图式表达：助力小学生对数学概念的理解

☉范春辉

当前的概念教学存在着这样的现象，教师只有描述性定义或者举例说明概念，加之学生头脑中对相关概念的印象不深刻，致使他们不能真正地理解概念。通常情况下，小学生在理解概念时可能会观察到事物的某一点或者是某一个方面，但是还不能对概念进行全面的思考和精准的运用。图式表达能让学生直观体验教材中的概念，能让他们在理清概念表达的思路的基础上实现思维逻辑上的发挥。因此教师在概念教学时就可通过图式表达指导学生开展进一步的探究，以获得更多能力与素养的生长。

一、利用图式表达，使抽象概念形象化

小学生还是以形象思维为主，因此在概念教学中教师要发挥他们形象思维的优势，可将抽象的数学概念形象化。当概念被形象化之后，不但增强了学生参与的兴趣，也对接了他们的认知特点。

以苏教版小学数学三年级上册《分数的初步认识》为例，课本上这样阐述分数的概念，分数表示一个数是另一个数的几分之几或一个事件在所有事件中的比例，换言之，把单位一平均分成若干份，表示这样的一份或几份的数叫做分数。对小学三年级的学生要直接理解这样严密的语言表达是有一定困难的，因此在教学中教师也不宜直接将这样的概念抛给学生。要想让学生能够理解分数的内涵与意义，教师可借助相关的数学图式，以帮助学生建构思维上的转换。

如图1所示，教师拿出一个月饼并当场平均分成两份。教师先是问学生，分成的两份是不是一样大，每份是不是都是这个月饼的一半，一半用哪个数来表示呢。学生在回答完前面的两个提问之后，教师总结说，刚才把月饼平均分成2 份，每份是这个月饼的一半，这一半就是它的二分之一。显然通过图式教师将分数的概念形象地表述出来。为了进一步地让学生感知分数，教师让学生对着图1说一说二分之一中的这个“二”表示什么意思，“一”又是表示什么意思。接着教师又将月饼平均分为四份，让他们说一说，每一份可以用怎样的分数表示。显然地，借助图式教师想让学生认识一般意义上的分数，也就说，让他们对分数的理解不仅仅局限在特殊的范例上。其实对概念的解读教师要抓住的就是一些关键的词语，分数的概念中，教师就要指导学生抓住“平均”这样的字眼。同样地，教师不是让他们死记硬背这个概念中要出现这个关键词，而是通过反例教学法，就是展示一些不正确的图式，进而加强对正确图式的理解。因此教师出示图2，并问出这样的问题：月饼这样分，能表示二分之一吗？这是为什么？

（图1）

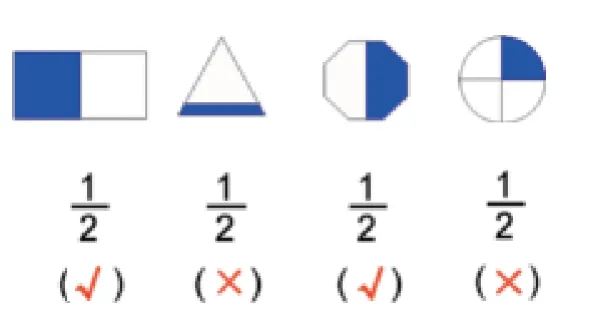
（图2）

可见通过图式的表达，学生能轻松地理解分数的概念，不需要去记忆复杂的文字表述，他们只需要借助图式就能说出分数的意义与内涵。同样地，借助图式他们也能说出这个概念中需要关注的点。因此图式表达改变了学生学习概念的方式，增强了学习的效果。

二、运用图式表达，使复杂概念简单化

图式表达之于概念学习就是以图表等方式将复杂的内容简单化，能让学生一目了然［2］。学生看文字不能明白的内涵，通过图表就能清晰地知道其中的意义。因此在概念教学中，教师要善于将文字的表述转为图表，将复杂的表述简单地呈现。

以苏教版三年级下册《小数的初步认识》这一章节为例，教师可以通过不同的语言表述将小数的概念展现出来。首先教师可以从分数的意义说起，比如，把整数1平均分成10份、100份……得到的十分之几、百分之几……可以用小数表示。教师可就这样的表述再做一个补充，一位小数表示十分之几，两位小数表示百分之几……教师发现这个概念还不够完整，又做了这样的补充：在小数里，每相邻两个计数单位之间的进率都是10。用语言将小数的概念向学生解释清楚是多么费劲的事，可这样的解释学生还是不能真正地理解什么是小数，因为这个概念从文字的层面看就显得复杂。学生还觉得复杂的一个原因就是小数是一个新的概念，他们很容易与学到的整数、分数等混淆起来，会让他们陷入学习的困境。教师可以借助图式帮助学生建构新的概念，让他们融入新的认知情境中。

因此教师就建立起如图3 所示的图式，图中教师展示的是一把直尺，上面标有尺度，这是学生熟悉的事物。图上还展现出学生熟悉的文具——铅笔，教师要让学生说出的就是这支铅笔的长度。学生一看就知道这支笔的长度在3 与4 之间，他们发现这不是一个整数，该怎样表达？教师趁机补充一句，在进行测量和计算时，如果遇到不能正好得到整数的结果，大家可用小数来表示。对着图式，教师这样解释小数的概念，不能正好是整数，显然地，学生对小数这个概念有了一个直观的感性的认识。教师接着就图三说，其中的1 份是十分之一，也可以表示0．1。教师补充问，假如其中的7 份就是十分之七，也可以表示成什么？学生回答0．7。教师再问这支铅笔的长度是多少厘米，学生回答出3．7 厘米。

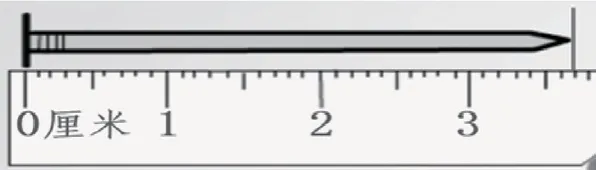
（图3）

可以看出来，图式之于概念学习不但将复杂变为简单，还将概念的运用也穿插进去，也就是说，图式表达不仅仅是阐述概念，也激发学生能力的生长。因此在教学过程中，教师遇到复杂的概念要尽量地帮助学生进行转化，以对接他们的最近发展区。

三、借用图式表达，使零散概念系统化

大多数学生在学习概念时还是采用死记硬背的方式，也就是说，他们将要运用到的一些定理、公式、定义等背得很熟练，以应付各种考试。但是在实际运用中会出现这样的情况，学生不能将一些概念系统化起来，总是孤立地去运用这些概念。比如他们会分别记忆长方形、正方形、三角形、平行四边形的面积公式，却不知道他们之间是有一定联系的，运用图式就能将这样的联系表述出来，进而也让这些概念之间形成一个相对完整的体系，更系统化，更有利于学生的综合运用。

以苏教版小学数学五年级上册《多边形的面积》这一章节为例，教师没有直接展示平行四边形的面积公式，即，如果用S 表示平行四边形的面积，用a 和h分别表示平行四边形的底和高，那么就有S=ah。

教师先是展示如图4 所示的图式，由于学生已经学过长方形的面积公式，教师就让他们把平行四边形转化成长方形，再求出面积。对着图式，学生将平行四边形沿高剪开，他们把剪下的梯形拼到另一边变成一个新的长方形。他们发现新的长方形的长相当于平行四边形的底，新的长方形的宽却又相当于平行四边形的高，进而基于对图式的演示，他们发现长方形的面积等于平行四边形的面积。借力图式，学生能将平行四边形的面积公式与长方形的面积公式联系起来，使他们构成一个认知的网，同时学生在遇到有关平行四边形的问题时，他们还会借助学习概念时的图式进行转化。

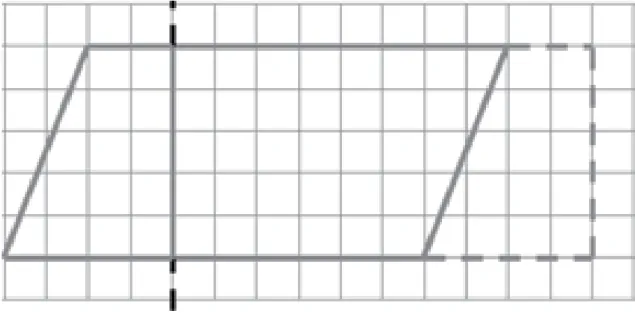
（图4）

四、结语

对数学概念的教学，教师不仅要通过文字的解释让学生理解，还要通过图表、几何图形等为他们搭建具象化支架，促进他们对概念的内化与运用。小学数学课本中概念繁多，比如数的概念、运算的概念、量与计量的概念等。学生对这些概念的学习一般都要先感知理解，再形成概念，最后再巩固应用。图式表达能促进概念的系统化、结构化，进而使学生更感性地认知概念。图式表达既展示概念的框架图，又彰显学生的思维模式，是他们理解数学概念的“助推器”。因此教师需要指导学生在充分理解的基础上进行有意义的图式建构。