关于BRK-代数的Pythgorean 模糊BRK-理想研究

宋爱丽

（喀什大学 数学与统计学院，新疆喀什 844000）

0 引言

自从Zadeh 引入模糊集概念以来，许多学者研究和讨论了模糊集概念的推广.文献[1,2] 引入了直觉模糊集的概念，研究了它的相关性质.文献[3]引入了Pythgorean 模糊集的概念，研究了它的相关特性.Pythgorean 模糊集是直觉模糊集的推广.随后模糊集、区间值模糊集、直觉模糊集等概念给广泛应用于各类代数系统，得到了许多有益的研究成果[4-7].作为BCK/BCI-代数的推广，文献[8]引入BRK-代数的概念，文献[9,10]讨论了BRK-代数的模糊结构，研究了BRK-代数的模糊子代数以及模糊BRK-理想及其相关性质.

本文将Pythgorean 模糊集的概念应用于BRK-代数，引入BRK-代数的Pythgorean 模糊BRK-理想的概念，研究它们的模糊特性，以丰富BRK-代数的模糊理论.

1 预备知识

为后面讨论方便，先给出一些相关概念和结论.

非空集X上的直觉模糊集形如

其中μA(x):X→[0,1]，νA(x):X→[0,1],并且对任意x∈X,0 ≤μA(x)+νA(x) ≤1.为方便起见用A=(μA,νA)表示直觉模糊集.

假设αA(x):X→[0,1]，βA(x):X→[0,1],并且对任意x∈X,0 ≤(x)+(x) ≤1,则称A=(αA,βA)为X上的Pythgorean模糊集[3].

定义1.1[8]设X为非空集合，常元为0，若X上的二元运算“*”满足:

则称(X;*,0)为BRK-代数.

性质1.1[8](X；*，0)为BRK-代数，则对任意x，y∈X，有：

（1）x*x=0；（2）x*y=0 仅当0*x=0*y；

（3）0*(x*y)=(0*x)*(0*y).

定义1.2[8]BRK-代数X的非空子集S称为BRK-子代数，若对任意x,y∈S都有x*y∈S.

定义1.3[8]BRK-代数X的非空子集I称为BRK-理想，如果下列条件成立：

（I1）0∈I；（I2）对任意x，y∈X，若0*(x*y)∈I，0*y∈I.

则0*x∈I.

定义1.4[9]设μ是BRK-代数X上的模糊集，若对任意x,y∈X，都有

则称μ是BRK-代数X上的模糊BRK-子代数.

定义1.5[10]设μ是BRK-代数X上的模糊集，若对任意x,y∈X,都有

(FI1)μ(0) ≥μ(x)；

(FI2)μ(0*x) ≥min{μ(0*(x*y)),μ(0*y)}.

则称μ是BRK-代数X上的模糊BRK-理想.

2 BRK-代数的Pythgorean 模糊BRK-理想

定义2.1设X是BRK-代数，A=(αA,βA)是X的Pythgorean 模糊集，若对任意x,y∈X，下列不等式成立：

则称A=(αA,βA) 是BRK -代数X的Pythgorean 模糊BRK-理想.

定理2.1BRK-代数的直觉模糊BRK-理想一定是Pythgorean 模糊BRK-理想，但是BRK-代数的Pythgorean 模糊BRK-理想未必是直觉模糊BRK-理想.

证明假设A=(αA,βA)是BRK-代数X的直觉模糊BRK-理想，则A=(αA,βA)是X的Pythg⁃orean 模糊集，并且对任意x,y∈X，有

故A=(αA,βA)是BRK-代数X的Pythgorean 模糊BRK-理想.

BRK-代数的Pythgorean 模糊BRK-理想未必是直觉模糊BRK-理想，如例1.

例1设S={0,1,2,3}，S上的二元运算*如下表：

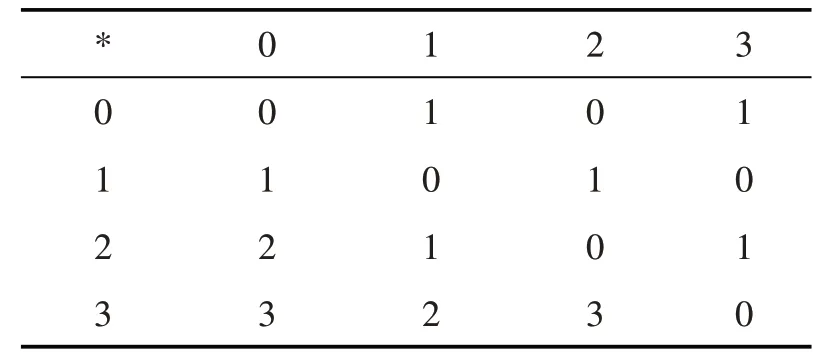
则(X,∗;0)是BRK-代数.

定义X上的Pythgorean模糊集为

则A=(αA,βA) 是BRK-代数X的Pythgorean 模糊BRK-理想.

定义X上的Pythgorean模糊集为

由于αB(0)+βB(0)=0.9+0.2=1.1 >1,因此B=(αB,βB)不是X上的直觉模糊集，从而B=(αB,βB)也不是X的直觉模糊BRK-理想.但B=(αB,βB)是BRK-代数X的Pythgorean模糊BRK-理想.

定理2.2如果A=(αA,βA)是BRK-代数X的Pythgorean 模糊BRK-理想，则BRK-代数X的非空子集A0={x|αA(x)=αA(0),x∈X}是BRK-代数X的BRK-理想.

证明显然0∈A0.对任意x,y∈X，若0*(x*y)∈A0，0*y∈A0，则

由于A=(αA,βA)是BRK-代数X的Pythgorean模糊BRK-理想，因此(0) ≥(0*x)，且

从而αA(0*x)=αA(0)，即0*x∈A0.故非空子集A0={x|αA(x)=αA(0),x∈X}是BRK-代数X的BRK-理想.

定理2.3如果A=(αA,βA)是BRK-代数X的Pythgorean 模糊BRK-理想，则BRK-代数X的非空子集B0={x|βA(x)=βA(0),x∈X}是BRK-代数X的BRK-理想.

定理2.4如果A=(αA,βA)是BRK-代数X的Pythgorean 模糊BRK-理想，则X的Pythgorean 模糊集A*=(μA,νA)也是BRK-代数X的Pythgorean 模糊BRK-理想.这里A*=(μA,νA)定义为：对任意x∈X，

证明假设A=(αA,βA)是BRK-代数X的Py⁃thgorean模糊BRK-理想，则对任意x,y∈X有

所以，的Pythgorean 模糊集A*=(μA,νA)也是BRK-代数X的Pythgorean模糊BRK-理想.

定理2.5若A=(αA,βA)和B=(αB,βB)都是BRK-代数X的Pythgorean 模糊BRK-理想.则A和B的交集A⋂B也是BRK-代数X的Pythgorean 模糊BRK-理想.这里

证明假设A=(αA,βA)和B=(αB,βB)都是BRK-代数X的Pythgorean 模糊BRK-理想,则对任意x,y∈X,有

由定义2.1 可知，A⋂B是BRK-代数X的Py⁃thgorean 模糊BRK-理想.

如果A=(αA,βA) 是非空集X上的Pythgorean模糊集，定义Pythgorean模糊集⊗A和⊕A满足：

定理2.6若A=(αA,βA)是BRK-代数X的Pythgorean 模糊集，则A是BRK-代数X的Pythg⁃orean模糊BRK-理想的充分必要条件是⊗A和⊕A都是BRK-代数X的Pythgorean模糊BRK-理想.

证明必要性.若A=(αA,βA)是BRK-代数X的Pythgorean模糊BRK-理想,则对任意x,y∈X,有

综上,⊗A和⊕A都是BRK-代数X的Pythg⁃orean模糊BRK-理想.

充分性.如果⊗A和⊕A都是BRK-代数X的Pythgorean模糊BRK-理想，则对任意x,y∈X,有

由定义2.1可知，A=(αA,βA)是BRK-代数X的Pythgorean模糊BRK-理想.

定义2.2设A=(αA,βA)是非空集X上的Py⁃thgorean 模糊集.对任意t∈[0,1],集合U(αA,t)=分别称为Pythgorean模糊集A的t-上水平截集和t-下水平截集.

定理2.7设A=(αA,βA)是BRK-代数X上的Pythgorean 模糊集.则A=(αA,βA) 是BRK-代数X的Pythgorean 模糊BRK-理想的充分必要条件是：对任意t∈[0,1]，非空集U(αA,t)和L(βA,t) 都是BRK-代数X的BRK-理想.

证明必要性.A=(αA,βA)是BRK-代数X的Pythgorean模糊BRK-理想，则对任意x,y∈X,有

因此0*x∈U(αA,t)，故非空集U(αA,t)是BRK-代数X的BRK-理想.类似地可以证明L(βA,t) 都是BRK-代数X的BRK-理想.

充分性.设对任意t∈[0,1]，非空集U(αA,t)和L(βA,t)都是BRK-代数X的BRK-理想.

故A=(αA,βA)是BRK-代数X的Pythgorean 模糊BRK-理想.

定理2.8若(X,*,0) 和(Y,*′,0′) 是两个BRK-代数.定义X×Y上的二元运算.满足:对任意(x,y),(a,b)∈X×Y,(x,y)∘(a,b)=(x∗a,y∗′b)，则(X×Y,∘,(0,0′)) 是一个BRK-代数.

定理2.9若A=(αA,βA)和B=(αB,βB)分别是BRK-代数X和Y的Pythgorean 模糊BRK-理想，则A和B的直积A×B=(αA×B,βA×B) 是BRK-代数X×Y的Pythgorean模糊BRK-理想.这里

证明设A=(αA,βA)和B=(αB,βB)分别是BRK-代数X和Y的Pythgorean 模糊BRK-理想，则对于任意(x,a),(y,b)∈X×Y,有

因此A和B的直积A×B=(αA×B,βA×B) 是BRK-代数X×Y的Pythgorean模糊BRK-理想.

定理2.10若A=(αA,βA)和B=(αB,βB) 是BRK-代数X 的Pythgorean 模糊BRK-理想，则A和B的直积A×B=(αA×B,βA×B) 是BRK-代数X×X的Pythgorean模糊BRK-理想.

3 结论

本文在BRK-代数中引入了BRK-代数的Py⁃thgorean 模糊BRK-理想的概念，讨论了它们的相关性质.得到了BRK-代数的Pythgorean 模糊BRK-理想关于交运算和直积运算的封闭性质.本文相关概念和结果能够推广到其他相关代数系统.