利用双树复小波特征进行蛋白质二级结构预测

陈 璐，高翠芳，鲁海燕

江南大学 理学院，江苏 无锡 214122

蛋白质是生物生命活动的重要组成部分，主要由20种天然氨基酸组成，这些氨基酸不同的排列顺序和个数使得蛋白质具有多样的二级结构，根据Levitt和Chothia提出的蛋白质结构分类，蛋白质通常分为四种类别：All-α、All-β、α/β和α+β类，蛋白质二级结构分类对于更深入研究蛋白质三级结构和蛋白质的功能与相互作用具有重要意义。然而，随着基因组和蛋白质科学的快速发展，蛋白质结构分类的实验注释滞后于蛋白质数据库规模的急剧扩大。因此，急需开发自动确定和识别蛋白质结构类别的预测方法[1]。

预测蛋白质二级结构通常有两个步骤。首先，不同长度的蛋白质序列通过特征提取可以用固定长度的特征向量来表示，再将特征向量输入到某种分类算法进行预测。对于蛋白质序列特征提取研究，已经有学者提出了数理统计方法和频谱分析方法，如氨基酸组分特征[2]、伪氨基酸组成[3]、二肽及多肽组成[4-5]、多重进化矩阵[6]、基因序列信息[7]以及不同特征的融合等。同时也产生了大量的预测算法，其中包括统计学和机器学习方法，如最近邻方法（KNN）[8]、隐马尔可夫模型（HMM）[9]、贝叶斯网络[10]、人工神经网络（ANN）[11]和支持向量机（SVM）[12]等。

总结前人的研究可以发现，在将蛋白质序列转化为距离矩阵后，将其视作一种纹理图像，使用灰度共生矩阵和灰度直方图统计等方法提取其特征，输入分类器分类结果不是很高，为了改善这一问题，本文引入小波变换提取距离矩阵中的特征。双树复小波变换源于解决传统的二维离散实小波变换在图像处理中存在的一些局限问题，在图像处理领域取得了较好的使用效果[13-14]。双树复小波变换使用两对滤波器组对图像实现L级分解，用每个尺度下得到的6个方向子带计算它们的能量与标准差，依此构造特征向量。本文使用双树复小波变换完成对转化后的蛋白质距离矩阵的特征提取，后文中的实验证明此方法可以有效提高蛋白质二级结构的分类精度。

1 材料与方法

1.1 数据集

本文使用两个数据集，它们分别来自文献[15]和文献[16]，两个数据集中蛋白质序列的Cα原子三维坐标均来自PDB数据库。在下载数据的过程中发现，文献中有些蛋白质数据在PDB数据库中不存在，故本文选取Cα原子三维数据完整的蛋白质序列，最后得到第一个数据集总共包含197个蛋白质，其中48个All-α类、60个All-β、45个αβ类和44个α+β类，下文简称数据集A，第二个数据集总共包含1 656个蛋白质，其中440个All-α类、437个All-β类、342个αβ类和437个α+β类，下文简称数据集B。两个数据集中所含各蛋白质二级结构数据如表1所示。

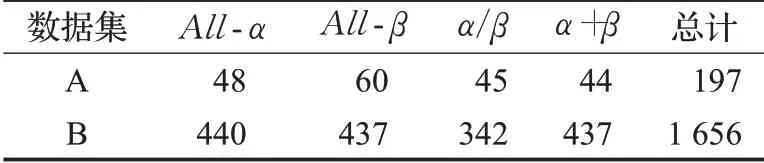
表1 数据集Table 1 Data sets

1.2 方法

1.2.1 距离矩阵中的纹理信息

建立预测方法的关键是提取蛋白质序列特征，使用蛋白质骨架描述其二级结构，也就是使用Cα原子的三维坐标，计算每条蛋白质链上所有Cα原子两两之间的距离，构成一个矩阵，这样的矩阵包含了蛋白质结构除手性之外足够的三维结构信息[17]，因此，可以提取蛋白质距离矩阵的特征对蛋白质三维结构比较。

设长度为L的蛋白质序列P i为：

其中，R1R2R3R4R5表示蛋白质序列P i的第一到第五个氨基酸残基，以此类推，R L表示蛋白质序列P i的最后一个氨基酸残基。则其骨架可定义为：

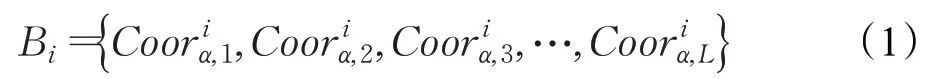
图1 不同蛋白质二级结构纹理图Fig.1 Secondary structure texture map of different proteins

纹理是图像的重要信息和特征，利用图像的纹理特征进行分类是一种有效的方法。提取图像纹理特征的方法有基于灰度直方图、灰度共生矩阵以及基于小波变换等方法，但图像的灰度直方图只统计了图像的一阶信息，灰度共生矩阵只是从粗的粒度描述了纹理的特征，二维小波变换存在平移改变性和有限的方向选择性等缺陷，Kingsbury提出的双树复小波变换[18]具有近似的平移不变性、良好的方向选择性和有限的数据冗余等优点，能从不同的方向提取图像的特征，丰富纹理信息。

1.2.2 双树复小波特征

二维双树复小波的定义为：

其中，i为虚数，i2=-1；ψh和ψg分别是正交或双正交的实小波，且形成Hibert变换对。双树复小波变换可以通过离散小波变换DWT实现，一个DWT产生实部，另一个DWT产生虚部。其分解过程如图2所示。

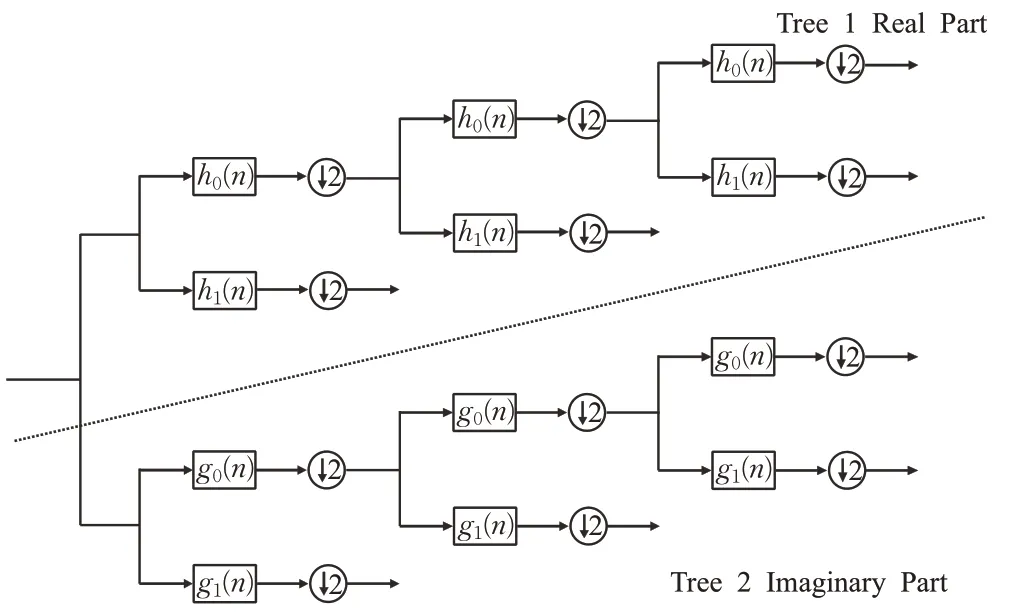
图2 二维DT-CWT的分解过程Fig.2 Decomposition of two-dimensional DT-CWT

由图2可以看出，双树复小波变换实质上就是使用两组低通滤波器h0(n)、g0(n)和高通滤波器h1(n)、g1(n)分别对输入的二维信号交替进行行列间的变换，分解出2个低频子带和6个不同方向(-75°,-45°,-15°,15°,45°,75°)的高频子带。这样将图像分解后就可以从更多方向来分析它的纹理特征。小波分解的级数越高，其获得图像在多尺度上的细节特征就越多，但是若分解级数太高，不仅特征图像的边界效应更明显，影响分类精度，还会增加小波变换的计算量，故本文将距离矩阵进行4级双树复小波分解，每个尺度下有6个方向子带Wl,n(i,j)，其中l=1,2,3,4，n=1,2,3,4,5,6。对这6个子带按照式（3）和式（4）计算能量E l,n与标准差σl,n[19]。

其中，M×N是子带图像Wl,n(i,j)的大小，μl,n是Wl,n(i,j)的均值。使用标准偏差和能量特征的组合，得到如下48维特征向量：

在将蛋白质序列经过上述步骤转化后，不同长度的蛋白质序列均可得到48维特征向量F。

1.2.3 分类预测

将两个数据集中的蛋白质按照上述方法提取特征，输入KNN分类器，其中K取5，每次实验采取十重交叉验证，计算5次实验结果的平均值作为最终结果，在计算两个特征向量的距离时，采用文献[20]中的规范化的欧式距离度量方法。

设F x、F y分别为两个蛋白质序列P i x和Piy所提取到的特征向量：

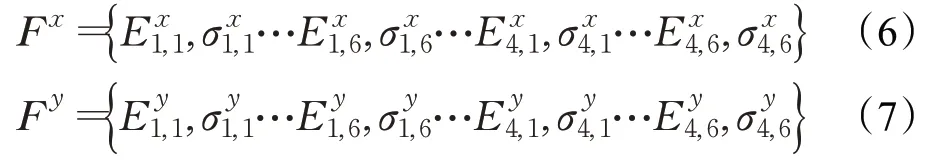
因此可得两蛋白质间的距离为：

其中

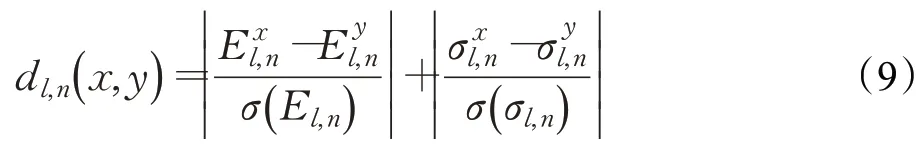
其中，l,n分别是小波变换的尺度与方向数，σ(E l,n)是E l,n在整个数据集上的标准差，σ(σl,n是)σl,n在整个数据集上的标准差。

2 结果与讨论

2.1 检验指标

为了检验方法的预测性能，本文采用5个指标：敏感性（Sensitivity）、特异性（Specificity）、准确率（Accuracy）、马氏相关系数（Mathew’s correlation coefficient）和总体准确率（Overall accuracies），这些指标越高说明预测结果越好。它们定义分别如下[21]：

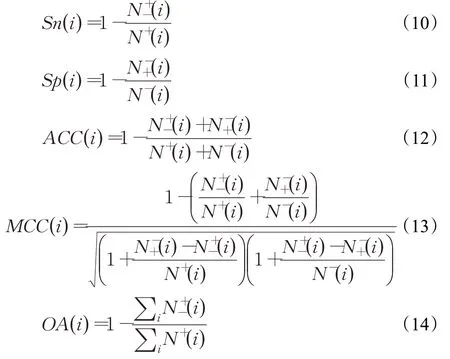
其中，i表示蛋白质的结构类别，本文中i=4，表示全部是第i类的蛋白质个数，表示被分类模型错误预测为其他类的第i类的蛋白质个数。表示全部其他类的蛋白质个数。表示被分类模型错误预测为第i类的其他类蛋白质个数。

2.2 预测结果及对比分析

按照上述双树复小波特征提取和KNN分类方法，在数据集A和数据集B这两个数据上的预测结果如表2和表3所示。

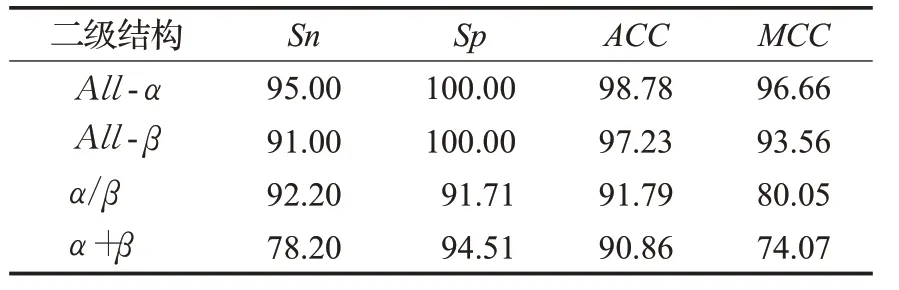
表2 数据集A性能预测Table 2 Data set A performance prediction%

由表2和表3可见，当使用双树复小波变换提取距离矩阵的纹理特征时，在两个数据集上的表现都很好，四个指标结果大部分范围在94%~100%，特别在数据集A的All-α和All-β这两个结构类别上，特异性（Specificity）达到了100%。这是因为双树复小波变换使用了两棵树对图像进行变换，增强了纹理信息的表达。为了便于对比，本文还按照下述方法提取了距离矩阵的其他特征。（1）提取灰度直方图统计特征[22]，即计算图像的均值、方差、对比度、三阶中心矩、四阶中心矩、均匀性和熵，得到7维特征向量。（2）提取灰度共生矩阵特征，即根据距离矩阵计算0°、45°和135°这3个方向的灰度共生矩阵，再计算每个方向上灰度共生矩阵的对比度、相关性、能量和均匀性这四种特征，最终得到12维特征向量。（3）提取小波能量特征，即用sym4小波包对距离矩阵进行4级分解，计算相应近似系数的能量百分数Ea和相应的水平细节系数Eh、垂直系数Ev、对角细节系数能量的百分数Ed，这样就得到13维特征向量。将上述特征向量分别输入KNN分类器分类，KNN中K取值都为5。表4和表5列出了数据集A和B分别提取上述四种特征的KNN分类结果。

表3 数据集B性能预测Table 3 Data set B performance prediction%

表4 数据集A结果比较Table 4 Comparison of results of dataset A%

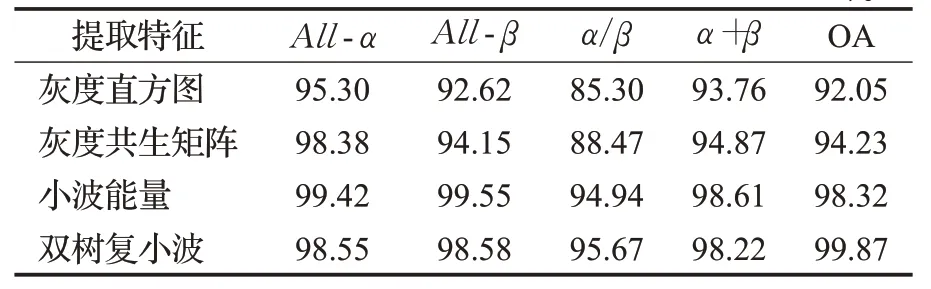
表5 数据集B结果比较Table 5 Comparison of results of dataset B%

由表4和表5可见，提取距离矩阵的双树复小波特征，在数据集A和数据集B上分类总体准确率分别是89.33%和99.87%，比灰度直方图统计特征和灰度共生矩阵特征都高出许多，对于每一个二级结构分类，准确率都有不同程度的提高。在部分结构类别上，双树复小波特征比小波能量特征略低，但总体来说，本文方法更可靠些。

为了证明本文提取特征的方法效果不依赖于分类算法，实验中还使用了SVM分类器分类，借助由台湾大学林智仁教授开发设计的一个易于使用和快速有效的SVM软件包LIBSVM，其中SVM中的主要参数（最佳惩罚参数c和核函数参数g）由网格搜索法得到，核函数选取RBF，每次实验采取十重交叉验证，计算五次实验结果的平均值作为最终结果。不同特征提取方法使用LIBSVM分类总体准确率如表6所示。

表6 不同方法在两个数据集上的结果比较Table 6 Comparison of results between different methods on two datasets %

由表6可以看出，利用SVM分类器分类，相对于前面三种特征表示方法，双树复小波特征在数据集A上分别高出了7.15、5.72和4.84个百分点，在数据集B上结果分别高出了3.51、1.69和0.53个百分点。为了更直观地体现本文方法的有效性，本文将在数据集A和数据集B上使用不同方法提取特征的总体准确率表示成图3。

从图3（a）和（b）中可以看出，提取的灰度直方图统计特征、灰度共生矩阵特征准确率总体来说比提取小波变换特征低，这是因为灰度直方图只是提取了图像的一阶统计信息，很难反映图像像素的空间位置等相关信息。灰度共生矩阵只是从比较粗的粒度描述纹理的特征，缺少对图像纹理的整体空间分布特征，而小波变换可以把图像分解到多个频带中，且具有方向性，充分挖掘图像的纹理和细节信息。使用双树复小波变换的准确率比小波能量特征要高一些，这是因为小波变换在处理图像时有两个主要的缺点，即平移改变性和有限的方向选择性，而双树复小波变换正好解决这两个问题，能够从不同方向提取图像信息，丰富图像的特征。

3 结束语

本文引入双树复小波变换提取蛋白质的结构特征，对于蛋白质的距离矩阵的纹理信息，利用了双树复小波变换的近似的平移不变性、良好的方向选择性和有限的数据冗余等优点，避免了传统提取图像的灰度共生矩阵缺少图像纹理的整体空间分布特征的缺陷，以及离散二维小波变换在处理图像时的局限性，使用KNN、SVM两种分类器对提取到的特征向量进行分类验证，预测结果较好，其中使用SVM在两个数据集上的分类结果分别达到了98.50%和99.29%，蛋白质序列还有许多其他特征提取方法，比如经典的伪氨基酸组分方法，未来研究可以尝试对传统方法进行改进，或者与本文方法结合运用，以及将本文方法应用于其他具有纹理特征的蛋白质数据。