融合时间加权信任与用户偏好的协同过滤算法

张岐山，朱 猛

福州大学 经济与管理学院，福州 350108

在互联网信息过载的时代，推荐系统可以帮助用户快速获取自身需要的信息，且在解决难以描述的需求以及个性化需求上表现更好[1]。推荐系统主要包括协同过滤推荐、基于内容的推荐以及混合推荐[2]，其中协同过滤推荐在互联网推荐系统中应用的较多，尤其是基于用户的协同过滤算法，从用户的角度挖掘用户潜在的兴趣偏好，更符合个性化的推荐，此外，协同过滤应用范围也较广，对于无法量化的特征，仅使用评级数据也能取得较好的效果[3]，但由于数据稀疏性[4]以及用户兴趣动态变化[5]等问题导致推荐精度不足。

现实中，人们更愿意相信好友推荐的物品，因此信任在推荐系统算法中的应用受到了广泛的关注，尤其对于数据稀疏的问题，辅助使用用户信任关系的效果比传统的协同过滤更好[6-7]。文献[8]定义了两种信任类型，分别是从用户角度和项目角度的正确推荐占比，并把它们整合到标准的协同过滤的框架中，提高了推荐的准确性。文献[9]使用用户间的预测误差和用户共同评分数来计算直接信任，对于没有共同评分项的用户，构建间接信任来缓解数据稀疏性。文献[10]利用用户之间的交互次数得到直接信任，并通过等效电阻理论的距离度量方式计算间接信任，但计算直接信任时忽略用户的评分。

虽然信任在推荐算法中的应用在一定程度上改善了推荐结果，但在数据极其稀疏时，根据用户对项目的评分行为建立的用户关系并不能反应出用户关系的真实情况，通过用户对项目标签的偏好程度能进一步挖掘出用户之间的偏好关系。文献[11]将用户对项目标签的评分频率作为用户对项目标签的偏好程度。文献[12]将用户对项目标签评分的平均值与该用户对所有项目的评分平均值的比值作为用户对项目标签的偏好程度。以上研究通过用户对项目标签的偏好程度缓解了数据稀疏性。

然而，用户兴趣并非静态的，而是会随时间而变化，因此越来越多的学者在推荐系统中融入时间因素。文献[13]提出基于遗忘曲线规律进行时间衰减，拟合艾宾浩斯曲线得到用户兴趣随时间变化的函数。文献[14]提出了一种融合时间因素和用户评分特性的协同过滤算法，将用户对项目评分的时间间隔作为时间权重并融入到预测偏好得分中进行推荐。文献[15]使用logistic作为时间衰减函数，并将其考虑进相似度的计算中，提高了推荐精度。以上融合时间因素的算法均改善了推荐精度，但没有考虑到用户评分时间的不均匀，仍有进一步优化的空间。

针对以上问题，本文提出了融合时间加权信任与用户偏好的协同过滤算法。该算法首先结合用户评分的相对时间间隔和用户在该时段的评分数量占比计算出时间权重，根据用户之间共同的评分项目并加入用户对项目的时间权重得出用户的直接信任。其次，将信任传递的中间节点的个人信誉度作为信任传递路径的可靠性权重得到间接信任。然后，结合用户对项目标签的评分数量占比以及评分值占比得到用户对各个项目标签的偏好程度，建立用户-项目标签偏好矩阵，计算出用户之间的偏好相似度。最后，综合用户信任度与偏好相似度对用户进行推荐。本文的贡献主要体现在以下三个方面：

（1）考虑到用户评分时间的不均匀，结合用户评分的相对时间间隔和用户在该时段的评分数量占比计算出时间权重，并将时间权重融入到直接信任计算中，缓解用户兴趣动态变化的问题。

（2）考虑传递中间节点的个人信誉度，将信任传递的中间节点的个人信誉度作为信任传递路径的可靠性权重得到间接信任，缓解数据的稀疏性。

（3）综合考虑用户对每个项目标签的评分数量占比以及评分值占比的影响，对二者进行调和平均，建立用户-项目标签偏好矩阵，进一步缓解数据的稀疏性。

1 融合时间加权信任与用户偏好的协同过滤算法

1.1 融合时间因素的直接信任计算

1.1.1 时间权重的改进

用户的兴趣会随时间的变化而变化，在早期对某个项目不感兴趣的用户可能过段时间会产生兴趣，所以用户最近对项目的评分更能反映用户当前的兴趣。

一些学者[14-16]使用用户评分时间间隔来刻画用户兴趣变化，这种方法的理想状态是每个用户评分时间间隔是均匀的，然而实际中并非如此，用户评分时间存在密集区和非密集区，此时，用户在一段时间内对评价项目的记忆程度不仅与间隔的时间长短有关，还与用户在该时段内评价的项目个数有关。通过结合用户相对评分时间间隔和用户在该时段的评分数量占比作为时间权重能够使密集区的时间权重适当减小，非密集区的时间权重适当增大，从而使用户兴趣随时间的变化过程更加平滑，在用户评分时间非均匀的情况下，提升刻画用户兴趣变化的准确程度。改进后的时间权重公式如下：

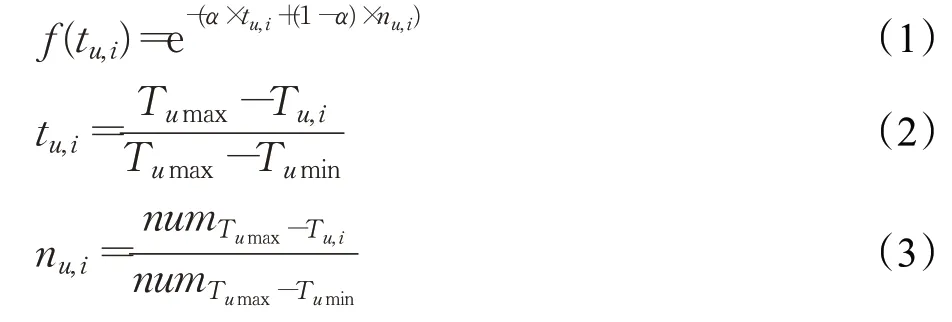
其中t u,i是指用户u对项目i评分的相对时间间隔，n u,i表示用户在T u,i到T umax的时段内的评分数量占比，Tu,i表示用户u对项目i的评分时间，T umax和T umin分别表示用户u最晚和最早的评分时间，numT umax-Tu,i表示用户u在T u,i到Tumax的时段内的评分个数。

1.1.2 融合时间因素的直接信任度

传统的信任模型忽略了时间对用户兴趣变化的影响，从而在一定程度上影响了推荐的准确性。JMSD在计算用户之间的相似关系已被证明具有较好的性能[17]，但是没有考虑到时间因素，因此，本文将改进后的时间权重融入到JMSD来衡量用户之间的直接信任关系，公式如下：

考虑到用户之间的评分偏好不同，有的用户评分比较宽松，评分较高，有的用户评分比较严格，评分较低，定义信任调整因子来增强信任，公式如式（5）所示，其中，μu和σu分别表示用户u的评分均值和评分方差。

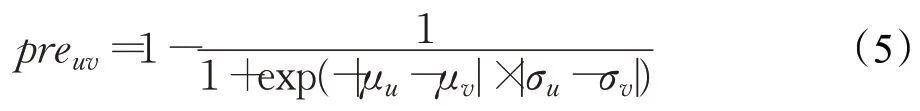
信任具有非对称性，比如用户A信任用户B，但用户B不一定信任用户A，或者用户B信任用户A，但信任的程度不一定相同，所以用户u对用户v的直接信任的公式如下：同理，用户v对用户u的直接信任为：

1.2 间接信任计算的改进

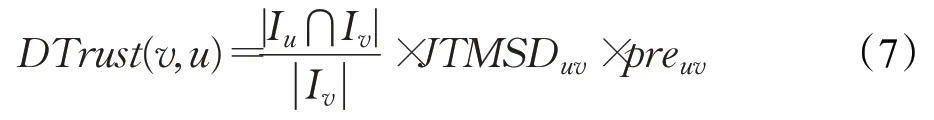
直接信任是根据用户之间共同评分项目的基础上进行的，而有的用户之间可能没有共同评分的项目，从而导致没有信任关系，为了更进一步的挖掘用户之间的隐藏信息，考虑信任的传递性。如果用户a信任用户b，用户b信任用户c，则认为用户a也信任用户c。传递信任随着用户增多信任度减少，以及传递的路径越长，存在的误差越大，所以本文采用两级路径传播。

当用户u和v之间只存在一条传递路径时，间接信任为该条路径上最小的直接信任值，当存在多条传递路径时，采用最小-最大复合的方法得到间接信任[9]，但该方法没有考虑用户的个人信誉度。由于本文的直接信任是依据用户之间的共同评分项得到的，而用户个人信誉度是由用户的评分数量以及评分准确度组成[18-19]，用户的评分数量越多、评分准确度越高，则用户的个人信誉度越高，通过计算得到的该用户对其他用户的信任值也越可靠。其中用户的个人信誉度PT(u)为：

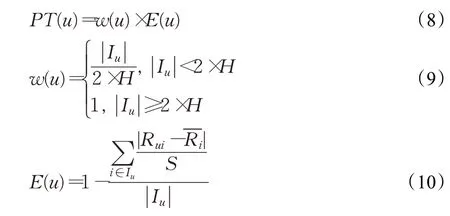
其中，w(u)、E(u)分别为评分数量权重和评分准确度，H为所有用户的平均评分个数，|I u|表示用户u的评分个数，S为项目的最高评分。

因此，考虑用户的个人信誉度，使用中间节点的个人信誉度作为该路径的可靠性权重，先选取每条传递路径的最小直接信任，其次将每条传递路径的中间节点的个人信誉度与对应的最小直接信任相乘，选出产生最大值的传递路径，进而取该条路径上的最小信任值作为间接信任。改进后的间接信任的公式如下：

其中，K表示用户u和用户v之间共同信任的用户集合，k*为得到的最可靠的传递路径的中间节点。

综合用户的直接信任和间接信任，则用户间的最终信任如下式所示：

1.3 用户偏好相似度的改进

用户对项目标签的偏好程度可以反映出用户对各种类型的电影的喜好程度，用户之间对项目标签的偏好程度越相似，他们之间的偏好相似度就越高，当数据非常稀疏，用户之间的共同评分项很少时，通过用户之间对项目标签的偏好相似程度综合考虑用户之间的共同评分项以及非共同评分项，能极大缓解数据稀疏性。在计算用户对项目标签的偏好程度时，文献[11]没有考虑评分值的大小；文献[12]忽略了用户在项目标签上的评分数量。然而假设用户A对项目标签x1的评分记录为[4，4，4，4，4，4]，对项目标签x2和x3的评分记录分别为[5，5]、[2，2，2]，则显然γA,x1＞γA,x2＞γA,x3，γA,x表示用户对项目标签的喜好程度。因此，本文中用户对项目标签的偏好程度由重要性权重和评分率权重两部分组成。

（1）重要性权重

重要性权重是指用户在所评价过的项目中，每个项目标签包含的项目数量所占的比例，计算公式如下：

其中，N u,x表示用户u评价过属于标签x的项目的数量。

（2）评分率权重

评分率权重是指用户在所评价过的项目中，每个项目标签的评分和与该用户所有评价过的项目的评分和的比值，计算公式如下：

Sumu,x表示用户u对属于标签x项目的评分和，Sumu表示用户u的评分总和。

重要性权重和评分率权重分别从用户对项目标签的评价数量以及评分值两个角度刻画用户对项目标签的偏好程度，本文认为二者对获取用户对项目标签的综合偏好程度同等重要，当重要性权重和评分率权重同时大时，用户对项目标签的综合偏好程度才大。因此，对二者采用调和平均计算用户对项目标签的综合偏好程度，且调和平均受极小值的影响比受极大值的影响更大，在用户对项目标签的评价数量占比较大、评分值占比较小或者评价数量占比较小、评分值占比较大的情况时，能够获得更加合理的综合偏好程度。用户对项目标签x的综合偏好程度γu,x的公式为：

通过提取项目特征能缓解推荐系统中存在的数据稀疏性问题[20]，由于项目标签远小于项目数量，且一个项目又可包含多种项目标签，则根据用户对项目标签的综合偏好程度建立用户-项目标签的偏好矩阵在稀疏程度上远小于用户-项目评价矩阵的稀疏程度，根据偏好矩阵计算用户之间的偏好相似度，能够较准确地挖掘出没有共同评分项或共同评分项较少的用户之间的相似度，偏好相似度如式（17）所示，其中X为所有项目标签的集合。

1.4 融合信任度和偏好相似度推荐

本文通过设置参数β，综合考虑用户的信任度和偏好相似度，将用户之间的偏好相似度和信任度进行线性加权，见公式（18）：

根据融合后的权重weight(u,v)，从大到小进行排序，取前top-S个用户作为最近邻居集S u，用户u对项目i的喜好程度p ui可由公式（19）计算得出：

2 算法描述

2.1 算法步骤

融合时间加权信任与用户偏好的协同过滤算法的具体推荐步骤如下：

输入：用户项目评分矩阵，用户评分时间矩阵以及项目标签矩阵。

输出：用户的推荐列表

步骤1通过用户评分时间矩阵和式（1）计算用户对已评价项目的时间权重，将时间权重融入JMSD中，然后依据公式（6）、（7）计算用户之间的直接信任。

步骤2根据公式（8）~（10）计算出用户的个人信誉度，将个人信誉度作为信任聚合的权重，利用公式（11）、（12）得到用户之间的间接信任。

步骤3根据式（13）得到用户之间的综合信任度。

步骤4通过项目标签矩阵以及式（14）~（16）建立用户-项目标签的偏好矩阵，然后利用公式（17）计算用户之间对项目标签的偏好相似度。

步骤5将用户之间的综合信任度与偏好相似度进行线性加权得到用户之间的综合相似度。

步骤6取步骤5中得到用户综合相似度进行降序排列，并取前S个用户作为最近邻居集。

步骤7根据式（19）计算用户对未评价项目的喜好程度，并对其进行降序排列，取前k个项目作为推荐列表。

步骤8重复步骤6和7，为所有用户生成推荐列表。

2.2 算法分析

本文提出的融合时间加权信任与用户偏好的协同过滤算法主要由两部分组成，一部分是考虑用户兴趣动态变化的信任关系度量算法，这部分算法结合用户评分相对时间间隔与用户在该时段的评分数量占比作为时间权重，能够使用户评分密集区的时间权重适当减小、非密集区的时间权重适当增大，使用户兴趣随时间的变化过程更加平滑，在一定程度上缓解由近期处于非密集区的用户兴趣随时间变化过快的问题，进而获取更准确的用户近期信任关系，提升推荐精度，同时，直接信任是依据用户之间的共同评分项，而用户的评分数量越多、评分准确度越高，用户的个人信誉度也越高，计算得到的该用户对其他用户的信任值也越可靠，因此，将传递中间节点的个人信誉度作为传递路径的可靠性权重，能够修正通过信誉度不高的用户获取间接信任的误差，进而提升推荐精度；另一部分是用户对项目标签的偏好相似性度量算法，这部分算法综合考虑用户对项目标签的评价数量与评分值，缓解用户对项目标签的评价数量与评分值出现一大一小的情况时，仅依据评价数量或评分值刻画出的用户对项目标签的偏好程度存在偏大或偏小的问题，从而提高用户偏好的准确度；最后通过融合这两部分算法能够更加准确地刻画用户偏好，对于用户之间共同评分项较少，使得获取的信任关系存在误差的问题，可以通过用户之间在项目标签的偏好相似度修正仅依靠信任关系进行推荐的误差，获取更精准的邻居集，从而缓解由数据稀疏性导致的推荐性能不高的问题。

3 实验结果及分析

3.1 实验数据集

本次实验采用的是MovieLens 100K数据集，Movie-Lens100k数据集是由GroupLens Research采集的多个用户对多部电影的评级数据以及电影标签信息等数据组成。该数据集包括943个用户对1 682部电影的100 000条评分，评分是1~5的整数，表示用户对电影的喜好程度，每个用户的评分个数不小于20条，电影有18种标签信息，主要包括喜剧、动作、科幻和动画等等，随机选取80%作为训练集，20%作为测试集。该电影数据集的数据稀疏度为93.70%。

3.2 评价标准

采用推荐系统常用的召回率recall@k、精确率precision@k以及F1值作为评价指标，k表示给用户推荐的列表长度。公式如下：其中，R(u)为本文算法通过训练集获得的电影推荐列表，T(u)为用户在测试集中评分的推荐列表。

3.3 实验结果分析

3.3.1 实验参数分析

（1）参数α的取值对TTUPCF算法的影响

实验中，取β为0.3，用户近邻个数为20，推荐列表的长度为20，α值从0增大到1，每次以0.1为单位递增，从而确定一个最优的α值。图1给出了α的取值对召回率和准确率的影响。从图1中可以看出，召回率和精确率随着α的取值总的来说是先增大后减小的趋势，在α=0.7时，召回率和精确率均取得最大值，比α=1时提高了1.20%，由此可以说明，结合用户相对评分时间间隔和用户在该时段的评分数量占比作为时间权重在刻画用户兴趣随时间变化的准确程度上比只采用用户相对评分时间间隔作为时间权重更高，具有更好推荐效果。

图1 α值对TTUPCF算法的影响Fig.1 Effect ofαon TTUPCF algorithm

另外，从实验结果可以看出，α取得最优值时较大，即用户相对评分时间间隔占比较大、用户在该时段的评分数量占比较小。这是由于当某些用户评分时间的非密集区的时间跨度较大时，用户评分数量占比越大，会使用户对非密集区的项目的遗忘程度急剧减小，产生的误差也越大。因此，在用户在该时段的评分数量占比较小时，才能有效地平滑用户兴趣随时间的变化程度。

（2）参数β的取值对TTUPCF算法的影响

实验中，取α为0.3，用户近邻个数为20，推荐列表的长度为20，β值从0增大到1，每次以0.1为单位递增，从而确定一个最优的β值，图2给出了β的取值对召回率和准确率的影响。从图2中可以看出，召回率和精确率随着β的取值先增大后减少，当β=0.3时，算法的召回率和精确率的表现最好，比β=0时提高了1.95%，说明在获取间接信任缓解数据稀疏性后，通过用户对项目标签的偏好程度计算用户的偏好相似度在一定程度上进一步缓解了数据稀疏性，提高了推荐精度。

图2 β值对TTUPCF算法的影响Fig.2 Effect ofβon TTUPCF algorithm

从实验结果中可以看出，β取得最优值时较小，即用户信任权重占比较大、用户偏好相似度占比较小，这是由于项目标签只有18种，划分的粒度较为粗糙，得到偏好相似度较信任度大得多。因此，在偏好相似度占比较小时，才能起到更好的调节作用。

3.3.2 对改进间接信任的实验分析

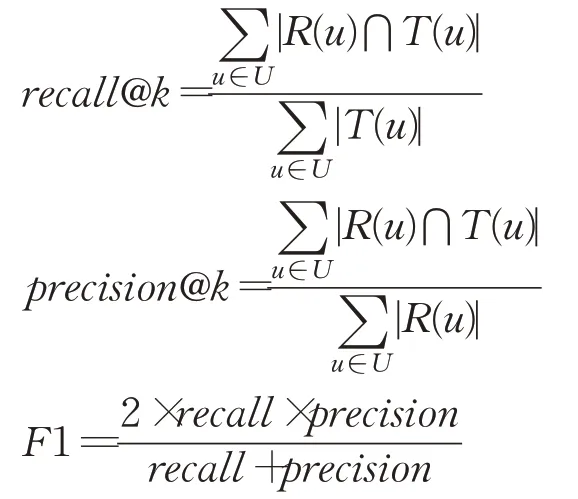
为了研究改进后的间接信任对本文算法的影响，将考虑信任传递中间节点的个人信誉度的模型与不考虑个人信誉度的模型进行对比。实验中将算法的参数均设为最优值，比较两者在推荐列表为20，用户近邻数从10增加到70时的F1值的变化情况。

从图3中可以看出，二者均在用户近邻个数为20时的F1值达到最大值，但考虑个人信誉度的模型的F1值均高于未考虑个人信誉度的模型。说明考虑个人信誉度得到的间接信任较未考虑个人信誉度的间接信任更为可靠，使本文协同过滤算法获取的邻居集更为精准。

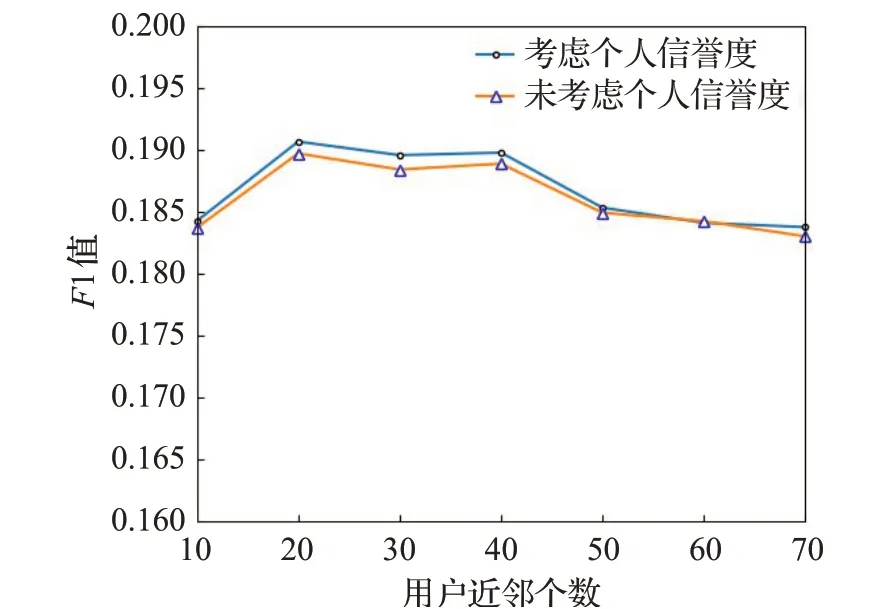
图3 考虑与不考虑个人信誉度对算法的影响Fig.3 Considering and not considering influence of personal reputation on algorithm

3.3.3 各算法性能对比

为验证本文提出的融合时间加权信任与用户偏好的协同过滤算法（TTUPCF）的性能，将TTUPCF与基于PCC的协同过滤（PCC）、基于JMSD的协同过滤算法（JMSD）以及文献[21]提出的一种融合隐式信任的协同过滤推荐算法（TCF）进行比较。

如图4所示，推荐列表长度取20，α=0.7,β=0.3，设置用户近邻个数从10增加到90，步长为10，分析用户近邻个数对各个算法的影响。从图4中可以看出，TTUPCF算法的F1值随着用户近邻个数先是增大，在近邻个数为20时达到最大值，然后缓慢降低，在近邻个数为60后趋于稳定，且在不同的近邻数下，TTUPCF算法的F1值均高于其他基准算法。其中，PCC在F1值上表现最差，这是由于PCC仅根据用户之间的共同评分项来计算用户之间的相似程度，存在严重的数据稀疏问题。JMSD在使用共同评分项来度量用户相似度的基础上考虑了用户之间的共同评分项的数量多少问题，因此在F1值上高于PCC，但未能有效缓解数据的稀疏性。TCF通过挖掘潜在的信任关系，并与用户之间的相似度进行调和平均作为推荐权重，在一定程度上缓解了数据稀疏性，因而在F1值上的表现要高于PCC和JMSD，但是未考虑到用户兴趣动态变化的问题。与上述三种算法相比，TTUPCF在度量用户间的关系时，同时考虑到了时间因素、信任关系以及用户的偏好相似度，有效地缓解了用户兴趣动态变化以及数据稀疏性的问题，能更加精确地获得相似用户群，有效过滤掉不相关用户对实验结果的影响。通过从多维度的角度全面衡量用户之间的关系，可以更加充分地挖掘用户偏好得到更为相似的近邻用户，相应的F1值也更高。

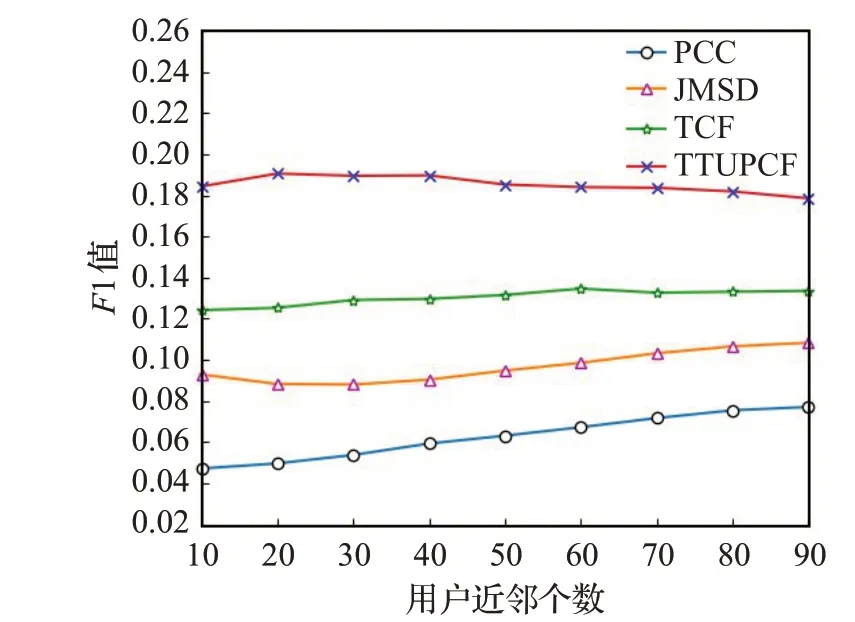
图4 不同邻近数下各算法的F1值对比Fig.4 Comparison of F1 values of each algorithm under different neighbor numbers

4 结束语

本文提出一种融合时间加权信任与用户偏好的协同过滤算法，考虑用户评分时间的不均匀改进时间权重，并将时间权重融入到JMSD中度量用户之间的直接信任，缓解用户兴趣动态变化的问题，并通过信任的传递性以及用户对项目标签的偏好来缓解数据稀疏性，进而获得更精准的邻居集，提高推荐精度。实验结果表明，与其他基准算法对比，本文算法在F1值有明显的提高。在接下来的工作中，考虑将用户信任与不信任与深度学习相结合来解决信任与不信任的传递问题，同时借助知识图谱挖掘用户与项目之间的潜在关联也是一个值得研究的方向。