时频空域混叠脉冲串辐射源信号直接定位算法

钟 华 阮怀林 孙 兵 张 奎

(国防科技大学电子对抗学院 合肥 230037)

1 引言

现代电子战的迅猛发展，对夺得制空权、制电磁权等战场主动权提出了更高程度的要求。对目标进行快速准确定位作为夺取战场主动权的重要环节，是当前研究的热点问题。有源定位由于隐蔽性弱、战场生存力较差等因素制约，应用受到较多限制。而无源定位通过被动接收辐射源信号，具有机动灵活且电磁隐蔽性强的特点，在军事情报侦察、机载侦察、资源考察等领域作用日趋显著。

随着现代战场态势复杂性的提高，无论是真实作战环境还是模拟演练环境，既定观测区域内通常同时存在多个目标辐射源，如一组辐射相似信号的舰船编队。对于侦察方而言，侦察站几乎同时接收到多个辐射源信号，接收信号混叠在一起，时域和频域也几乎重叠。多个目标的测量数据不能按照目标进行分类，导致辐射源个数和位置的确定无法实现。因此，如何有效地对这类辐射源信号进行精确定位，是迫切需要解决的问题。传统的无源定位技术，主要包括测向交叉定位[1，2]、到达时间(Time of Arrival， TOA)定位[3，4]、时差(Time Difference of Arrival， TDOA)定位[5，6]、频差(Frequency Difference of Arrival， FDOA)定位[7]以及同时利用多种定位方法的复合定位[8]等。多目标定位的基本思想是将关于多个目标的测量参数按目标进行分类，进而确定各个目标的测量数据，再利用传统的无源定位技术进行定位。本质上是将多目标定位问题转换为单目标定位问题。目前比较成熟的方法有两类：其一是通过信号分选将侦察到的多个信号进行分离[9]；其二是假定多目标数目已知，利用数据关联[10]等方法将关于目标测量的数据按目标分类，从而得到测量数据与辐射源目标的对应关系。当既定观测区域内存在多个时频空域混叠的辐射源信号时，多目标定位技术无法对混叠的辐射源信号进行有效分离，无法实现对混叠信号的定位。

直接定位法(Direct Position Determination，DPD)作为近些年的热门算法，可以直接利用接收到的信号对目标辐射源位置进行估计，避免了经典两步定位算法的中间观测量估计过程。Weiss[11]首次提出了DPD算法，算法利用多个观测站，将目标的角度信息融合在阵列流型中。同时，通过对接收数据进行离散傅里叶变换，将时延信息转换为相位信息，便于数据的处理，算法初次实现了单目标的直接定位。文献[12]研究了未知波形信号的DPD算法，结果表明MUSIC方法能有效降低算法的复杂度。文献[13]对存在多径效应、阵列误差、相位误差等情况下的DPD算法定位表现进行了研究。当辐射源发射的信号波形完全已知时，可以有效提高DPD算法的定位表现，2007年，Bar-Shalom和Weiss[14]提出了一种针对OFDM信号的DPD算法，该算法将OFDM信号中的先验信息和数据中的信息结合在一起，以获得OFDM信号辐射源的极大似然估计值，相比于传统的两步定位法，该算法在低信噪比下更接近于CRLB。同年，Amar等人[15]提出了针对多个窄带信号辐射源的DPD算法，该算法以迭代方式实现ML标准。2008年，Amar等人[16]将多普勒频移用于DPD算法，运用速度和位置已知的运动接收站对辐射源进行定位，分别在信号已知和未知状态下建立代价函数，最后寻找目标函数极值点对应的网格点，实现对辐射源的定位。2009年，针对静止辐射源，Weiss等人[17]提出了一种用移动接收站观测的基于时延和多普勒频移的极大似然估计器，为了实现所提出的方法，所有的观测信号必须输送到一个处理中心。与仅考虑时延或多普勒频率相比，所传送的信号需要更宽的带宽。同样用移动接收站对静止辐射源定位，文献[18]则将信号建模为高斯随机信号，即服从高斯分布的不确定性信号。尽管目标辐射源信号类型不同，代价函数的构建有所差别，但基本都是基于极大似然准则。

同时，国内专家学者也对直接定位算法的应用进行了很多有意义的探索。文献[19]先将接收到的辐射源信号划分为多个非重叠短时信号段，再利用同一接收机接收的短时信号之间的相干性，进行直接定位处理。通过相干求和，定位精度会随着两个短时信号之间时间间隔的增加而提高。王云龙等人[20]提出了一种联合时延与多普勒频率的直接定位改进算法 (Improved DPD， I-DPD)，利用极大特征值作为网格点的代价函数，该代价函数可以不受信号形式的限制，抑制了噪声的影响，提高了定位精度。文献[21]提出了一种针对严格非圆源的直接定位算法，通过有限次迭代，将接收到的信号进行解耦处理，大大降低了计算的复杂度，并推导了严格非圆阵的克拉美罗下界(Cramer-Rao Lower Bound，CRLB)。Wang等人[22]对恒定速度和恒定加速度的窄带移动辐射源定位情况进行了研究，针对两个运动模型提出了适合其特性的牛顿迭代算法，与多维网格搜索算法相比，该算法在不影响估计精度的前提下更有吸引力。文献[23]则使用多个接收机收集时延和多普勒拉伸信号来解决固定辐射源的定位问题，通过将宽带信号高精度地分解为少量的低维信号，并结合信号的时延和缩放信息，提出了一种计算效率高的DPD算法。以上列举的直接定位法往往适用于对单个辐射源信号进行定位，由于部分算法在建模过程中对必要的位置信息项进行了省略，导致侦察站接收到的部分位置信息遗漏或缺失，一定程度上影响了定位效果。

本文充分考虑相参脉冲串辐射源信号各脉冲之间的位置信息，利用直接定位算法无需对数据进行预处理的优越性，提出一种基于位置信息累积的直接定位(Localization information accumulation DPD， L-DPD)算法。与文献[20]的I-DPD算法相比，本文算法充分利用了脉冲串信号的位置信息，通过多个脉冲间的时差频差信息累加，达到更高的定位精度，实现对时频空域混叠辐射源信号的有效定位。

2 信号模型

假设地面固定辐射源位于p0=[x0，y0]T，有L个侦察站匀速直线运动，目标辐射源连续发出M个脉冲信号，第m个信号ym(t)模型为sm(t)exp(j2πfct)。其中，sm(t)是信号的包络，fc是信号的载频，时宽为Tm，带宽为Wm，且满足Wm ≪fc。第l个侦察站从tl，m时刻起对第m个脉冲进行观测时，对应的位

3 定位算法

忽略对数似然函数的常数项，则多站相参脉冲串直接定位的对数似然函数为

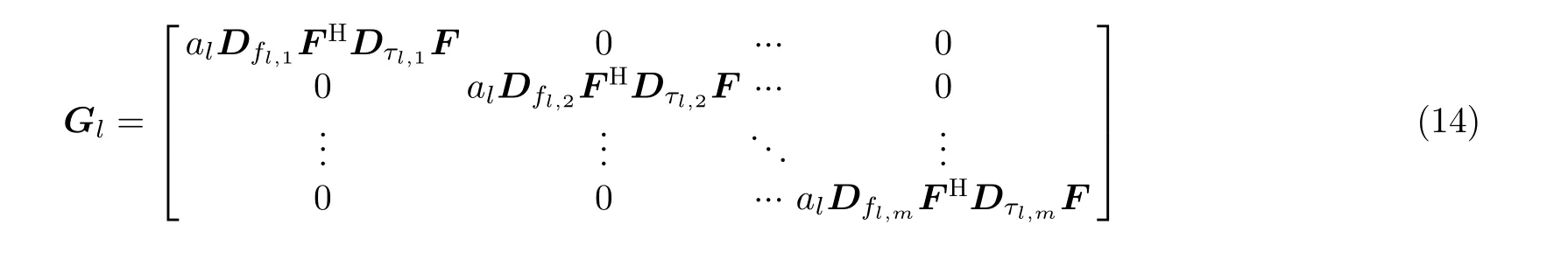
4 克拉美罗界

综上得

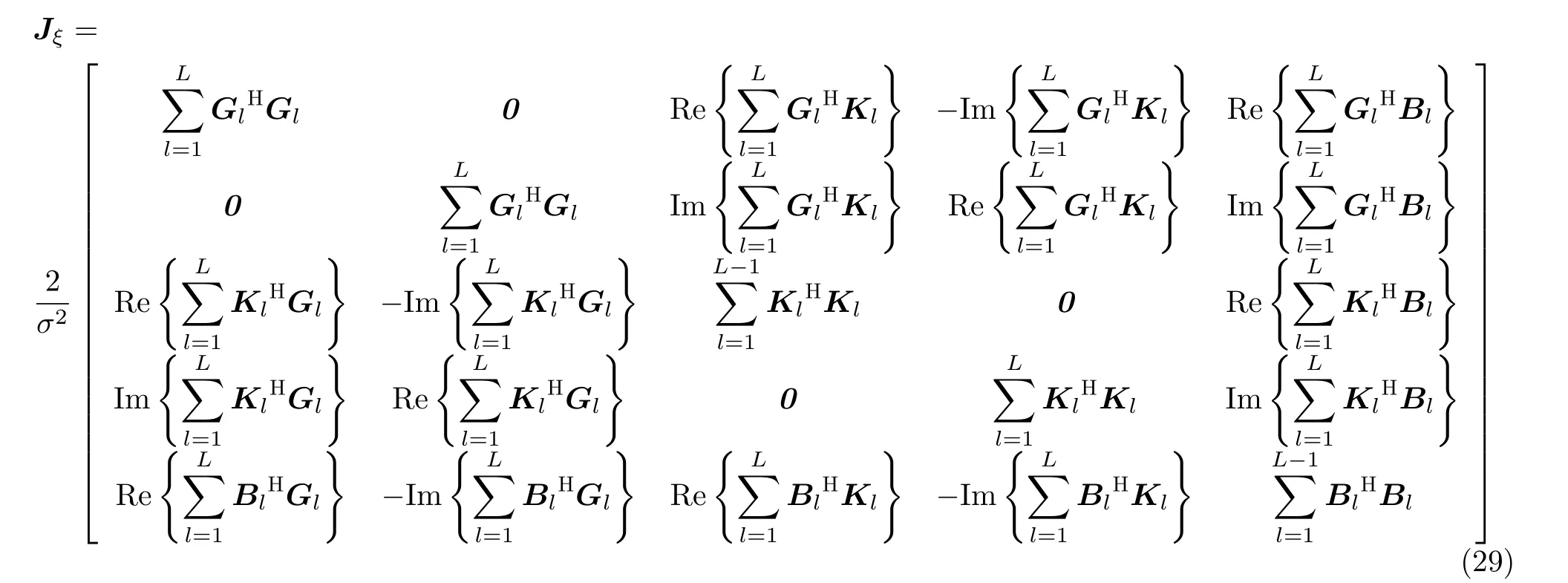
本文中，感兴趣的仅仅是定位精度，通过计算变量α的FIM矩阵，得到定位精度的CRLB。利用分块矩阵得到仅关于α的FIMJα为

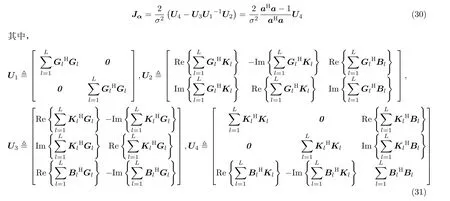
通过对矩阵Jα取逆，即可以得到关于辐射源位置p0的CRLB。

5 仿真分析

为了充分验证本文所提L-DPD算法的有效性，本节进行仿真实验。根据文献[20]的仿真实验参数，在目标间距设置时，分为目标间距较大和目标间距较小两种情况进行讨论。另文献[12]指出当辐射源间距低于100m时，定位效果会急剧恶化。结合以上文献在不同辐射源间距条件下的仿真结果，本文以100m为界限设置目标辐射源间距，并将仿真实验结果与文献[20]提出的I-DPD算法进行对比。

5.1 两目标间距较大

从图1可以看出，双站情况下，L-DPD算法比较清晰地展示了两个目标辐射源的位置，且与真实位置一致，定位结果中存在数目不多的伪峰。I-DPD算法的定位效果不是非常理想，峰值点周围出现了一定数目的旁瓣干扰，同时伪峰数目较多。从图2可以看出，三站情况下，L-DPD算法得到的目标成像更加清晰，并且没有伪峰。同样，I-DPD算法较双站情况下的定位效果也有所改善，伪峰数目相对减少，旁瓣干扰也得到了有效抑制。

图1 辐射源间距较大时定位结果对比(双站)

图2 辐射源间距较大时定位结果对比(三站)

分析以上结果可以看出：(1)侦察站数目相同时，L-DPD算法相比于I-DPD算法定位效果更好。该算法充分利用了位置信息项，通过多个脉冲的积累，大大增加了定位精度。即使在信噪比较低的情况下，依然能够有出色的定位效果。而I-DPD算法虽然在信噪比较高的情况下，能接近L-DPD算法的定位效果，但是随着信噪比下降，定位精度恶化，在信噪比较低情况下可能无法有效区分主峰，导致定位结果存在偏差。(2)侦察站数量的提高有效地改善了定位精度。在信噪比较低的条件下，可以通过增加侦察站数目提高定位效果。

5.2 两目标间距较小

当辐射源间距较小时，是否具有良好的分辨力是评价一个定位算法是否高效的重要指标。算法应在保证分辨力的前提下尽可能地提高定位精度。从图3可以看出，双站情况下，L-DPD算法对间距较小的辐射源信号具有较好的定位效果。算法在信噪比较低的情况下，依然能够有效区分两个辐射源的位置，此时辐射源周围有较小的旁瓣干扰。而I-DPD算法的估计结果中，有一处为[100.06，75.058]Tkm，与真实辐射源位置存在明显偏差，是伪主峰。从图4可以看出，三站情况下，L-DPD算法的定位结果相比双站情况不太理想，目标主峰周围的旁瓣干扰增多，同时出现一定数量的伪峰。而I-DPD算法得到的定位估计结果，对比双站情况下更加恶化。主峰周围的旁瓣高度和覆盖面更大，同时伪峰数量大大增加，算法依然只能对其中一个辐射源进行较精准定位。

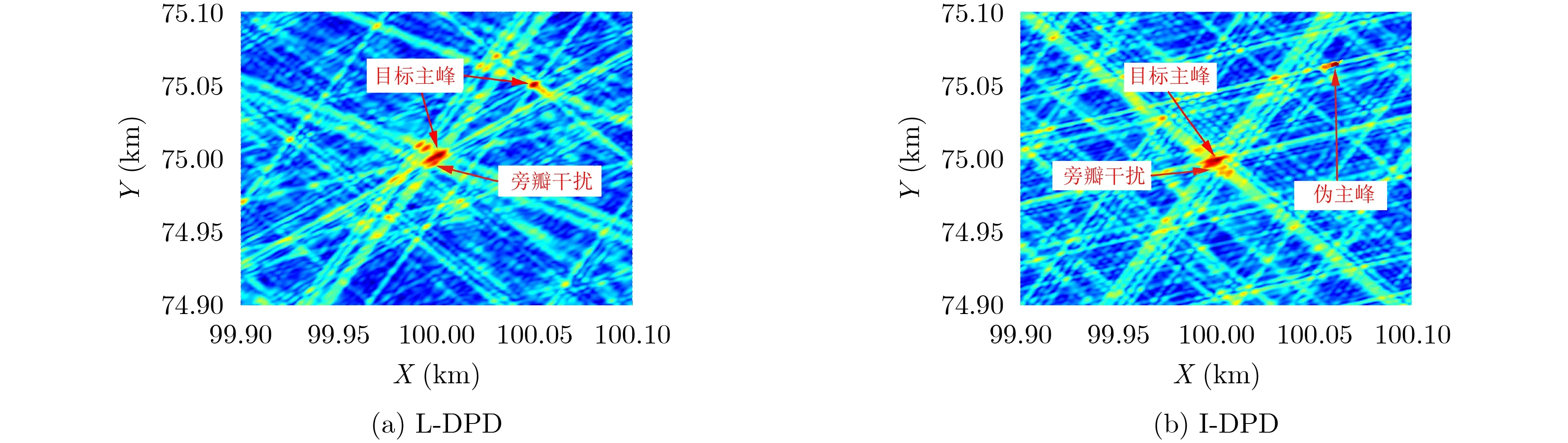
图3 辐射源间距较小时定位结果对比(双站)

图4 辐射源间距较小时定位结果对比(三站)

分析以上结果可以看出：(1)目标辐射源间距较小时，伪峰出现频率相对增加。原因是两个主峰之间的旁瓣位置较高，在信噪比较低的情况下，某个较高的旁瓣位置可能就会取代主峰，从而造成错误的定位结果。(2)对目标间距较小的两个辐射源定位，单纯地增加侦察站个数，反而对定位结果会有不好的影响。原因在于增加的侦察站会导致更多的时频差线汇集在拥挤的定位空间内，导致时频差线混叠，进而影响了定位精度。

5.3 定位误差曲线

图5和图6分别是在上述的仿真条件下，信噪比从—10 dB到30 dB变化时，定位误差均方根的曲线图。

图5 辐射源距离较大时不同算法定位误差图

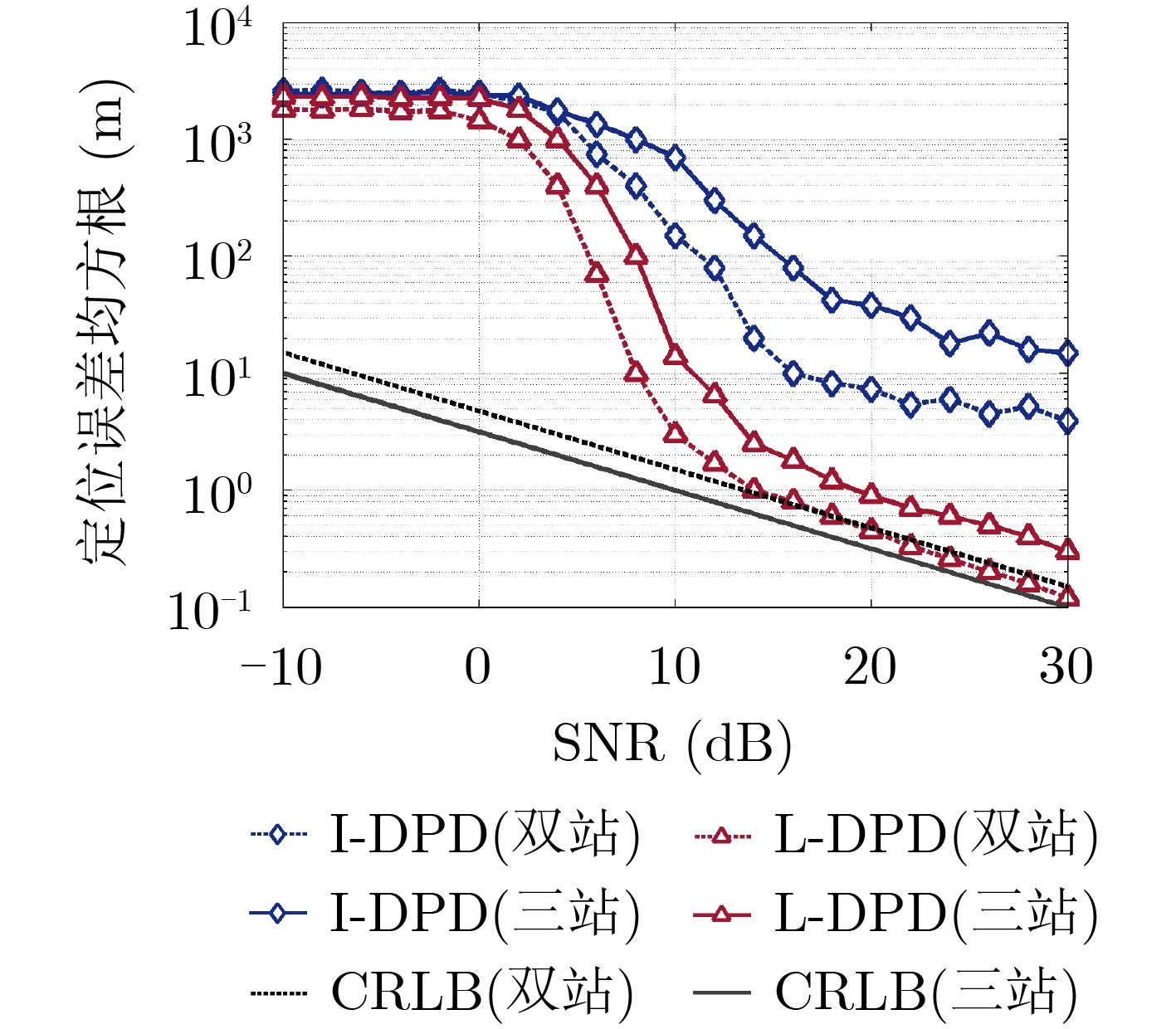
图6 辐射源距离较小时不同算法定位误差图

从图5可以看出，当辐射源间距较大时，L-DPD算法的定位效果明显优于I-DPD算法。在各自的信噪比门限内，定位误差一直保持高位。超过信噪比门限，随着信噪比的提高，算法的定位精度均有所改善。其中，L-DPD算法的定位精度提高较为明显。在信噪比10 dB的情况下，已可以达到较好的定位效果。而I-DPD算法在信噪比达到15 dB的情况下，才可以达到近似的定位精度。从图6可以看出，辐射源间距较小对定位误差的影响是非常显著的。在信噪比区间0～30dB，随着信噪比的提高，I-DPD算法的定位误差仅仅能有小的改善。与之对比，L-DPD算法得到的定位误差改善较为明显，尤其在信噪比5～15 dB区间内改善幅度较大。分析以上结果可以得出：(1)辐射源间距较大且信噪比较低时，增加侦察站个数可以有效提高定位精度。辐射源间距较大且信噪比较高时，双站定位已可以达到较高的定位精度。(2) 超过信噪比门限后，辐射源间距较小时的定位误差远远大于辐射源间距较大的情况。即使是分辨力出色的LDPD算法，在低信噪比较高的情况下仍然无法完全贴合CRLB。(3)在辐射源间距较小的情况下，LDPD算法的分辨力明显优于I-DPD算法。主要原因在于L-DPD算法充分利用了脉冲串信号的脉间信息，通过对多个脉冲串相参积累，有效积累了各侦察站关于时延和多普勒频移中位置参数的信息。而I-DPD算法由于在建模过程中省略了exp(-j2πfl，mτl，m)项，导致关于辐射源的位置信息部分缺失，导致定位误差通过多次的相关累积被持续放大，影响了算法的定位精度和分辨力。(4)当辐射源间距较小时，增加侦察站数量，时频差线混叠加剧，反而影响定位效果，导致定位精度下降；当辐射源间距较大时，适当增加侦察站数量，可以进一步提高定位精度。实际应用中，应综合考虑不同信噪比条件下，增加侦察站数量带来的定位精度提高和算法复杂度提高等因素，做出取舍。

6 结论

针对经典的直接定位法无法对时频空域混叠辐射源信号进行高分辨高精度定位的问题，提出了一种基于位置信息累积的脉冲串直接定位算法。通过建立确定性未知信号模型，利用傅里叶变换对构建离散采样信号，得出了高斯白噪声背景下基于时延和多普勒的最大似然直接定位算法。同时推导了确定性未知信号模型下的直接定位算法克拉美罗界。仿真结果表明，本文算法可以对时频空域混叠信号进行高分辨高精度定位。