基于Watterson模型的短波航空移动信道建模与仿真
2022-02-24李国军叶昌荣罗一平
李国军 马 欢 叶昌荣 罗一平
(重庆邮电大学超视距可信信息传输研究所 重庆 400065)
1 引言
短波通信(3~30 MHz)利用电离层对高频电磁波反射的机理实现长达数千公里的超视距通信,经多次反射可实现全球覆盖,是国家、军队远程通信、移动通信和应急通信的基本手段[1]。在卫星通信系统失效的情况下,短波通信是飞行器超视距远程指挥控制的主要手段,有时甚至是唯一手段。
在航空移动通信系统中,当飞行器做变速直线运动或圆周运动时,收发两端的相对运动将会使接收信号产生时变的多普勒频移和扩展。结合短波信道本身随机多径所带来的信号失真和多径时延,使得短波航空移动信道的衰落特性也更加复杂[2,3]。建立准确而有效的短波航空移动信道模型,能够有效加快技术迭代,降低实验成本,有利于短波通信技术在航空领域的进一步发展和推广应用。
短波传播主要是通过天波传播,依靠电离层反射可以跨越复杂地形环境实现数百乃至上千千米的通信。因此,短波信道建模与仿真的研究始于对电离层特性的探究。由于电离层本身的复杂性和时变性,我们很难用一个准确的模型来描述短波信道,目前典型的两种短波信道模型Watterson模型[4,5]和ITS模型[6,7]都是基于实测数据得到的统计性模型。其中Watterson 模型采用抽头延迟线结构,实现复杂度相对较低且全面描述了短波信道中的各种特性,所以成为ITU推荐的短波通信性能测试标准信道模型。对于航空移动信道的研究,文献[8—10]在超短波频段对航空信道的小尺度衰落进行统计建模并仿真。但目前超短波网络尚不能覆盖所有区域,在正在兴起的极地飞行中,短波几乎是地空超视距通信的唯一手段;文献[11]对短波移动信道模型进行了分析,但是模型结构简单,没有将移动场景的复杂性与信道衰落结合起来,故不能反映出短波移动信道的全部特性;文献[12]对无人机短波频谱监测信道的建模与仿真,只考虑了飞行器低速运动的状态。目前,对于短波航空移动信道,尚缺乏一个标准的信道模型。
本文以Watterson信道模型为基础,结合相对运动带来的多普勒效应的影响,提出并实现了一种适用于远距离航空移动通信的短波信道模型,并针对不同种类不同参数飞行器,对航空移动信道进行了差异化仿真。同时针对典型的民用航空场景,当航线航迹已知时,实现了对特定场景下的短波航空移动信道的定制化仿真,对短波通信在航空通信领域的发展与研究有重要的参考价值。
2 短波Watterson信道模型
短波电离层反射信道在时间和频率上都是时变的,但是Watterson 等人[4]通过长期测量和研究,提出短波电离层信道在有限时间(<10 min)和有限带宽(<12 kHz)条件下是稳定的,据此建立了一种静态的高斯型散射信道模型,即Watterson模型。该模型结构简单,如图1所示,全面描述了短波信道中的多径传播、衰落、多普勒频移和扩展等各种特性。
从图1可以看出,输入信号经过抽头延迟线后生成多条路径,每个抽头就相当于一种电离层传播模式或路径。抽头增益函数Gi(t)对每路的延迟信号进行调制来模拟信号在传播过程经历的衰落。最后,各路已调信号和加性噪声相加,形成最终的输出信号。Watterson模型的时变频响为

图1 Watterson短波信道模型

其抽头增益谱函数为

3 短波航空移动信道建模


由于飞行器的飞行状态会导致每一传播模式下不同的多普勒频移。对于民用航空信道而言,飞行器机动频率较低,飞行器飞行状态在较长时间内保持不变。而当飞行器的机动频率较高时(如无人机等),其运动速度的大小和方向在短时间内变化很快,飞行器的运动轨迹也难以估计。通常可以将轨迹分成很多小段,每小段都可以看成直线运动和部分圆周运动,如图2所示。
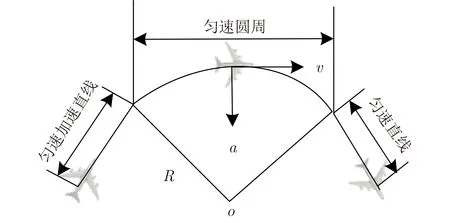
图2 飞行轨迹示意图
在航空移动信道中,当飞行器做变速运动或圆周运动时,每条路径内多普勒频移的快速变化会导致其多普勒扩展短时间内发生急剧变化。每条路径的多普勒频移与飞行器的移动速度有关,通常情况下,飞行器的速度公式为

其中,F为飞行器的牵引力,v为当前速度,f为飞行中所受空气阻力,其值与速度的平方成正比,k为比例系数,m为飞行器质量。为了避免飞行器在加速过程中超过最大速度,这里假设|v/vmax|≥0.8时,飞行器发动机的功率保持最大恒定,此时飞行器的飞行速度受最大功率影响,理论上加速度会逐渐降低,直至飞行器匀速飞行,如图3所示。
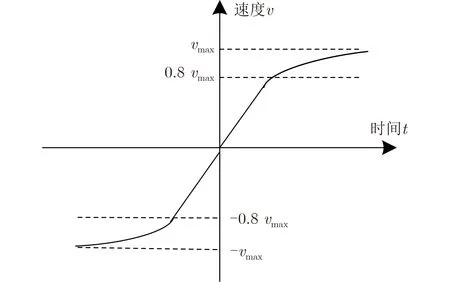
图3 飞行器速度上限变化

4 短波航空移动信道模型的仿真
短波航空移动信道模型的实现框图如图4所示。实际通信中,输入的短波信号的载波频率为3~30 MHz,但是为了便于数字信号处理,往往通过数字下变频技术分离出I, Q两路数字基带信号[14]。要构造一个短波航空移动信道,还需要确定每条路径的抽头增益函数。抽头增益谱函数主要由时变多普勒频移和多普勒频率扩展决定。此外,还要考虑多径效应以及实际短波信道存在的各种干扰和噪声。
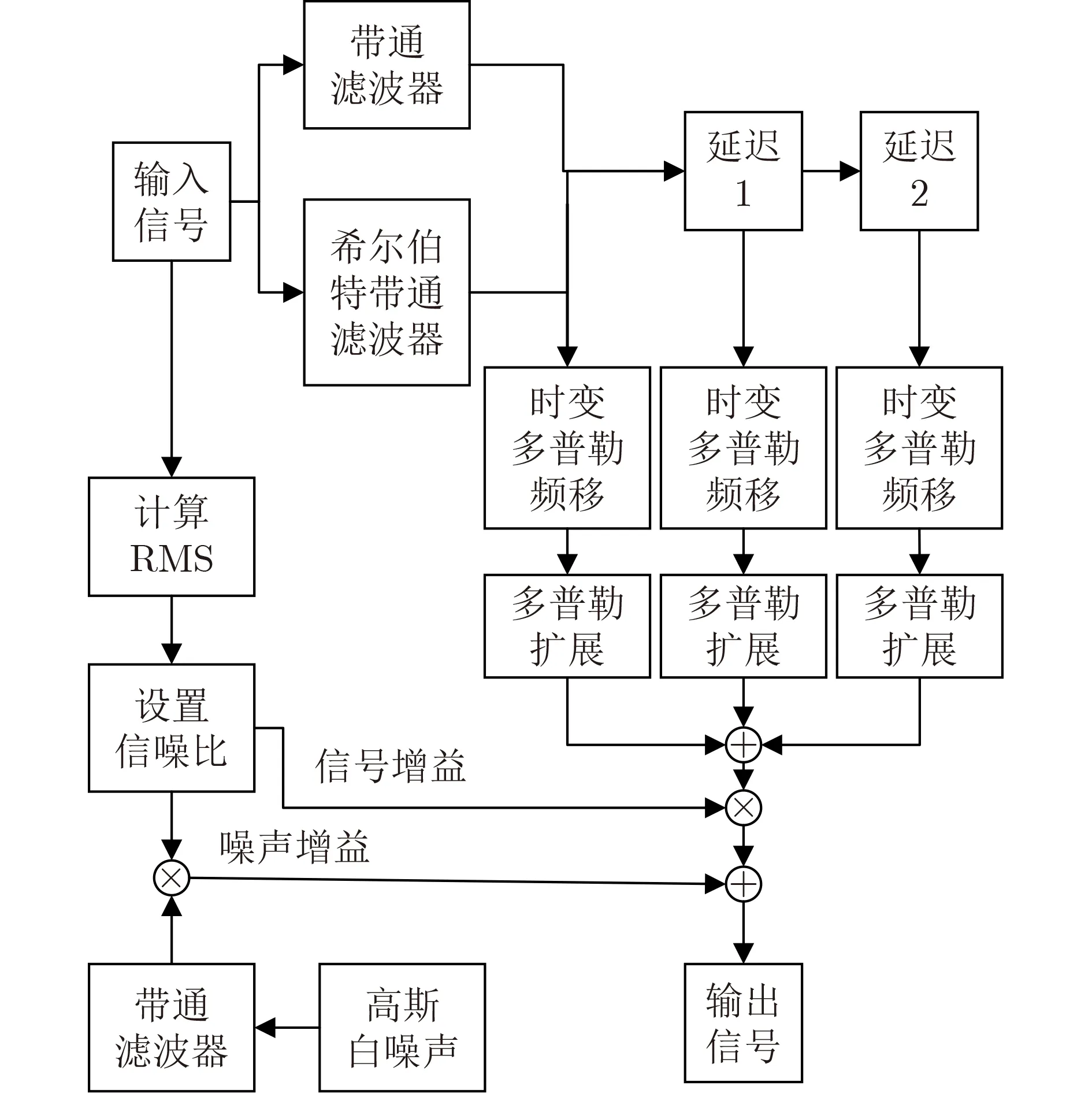
图4 短波航空移动信道模型的实现框图
4.1 希尔伯特滤波器
对于这两个带通滤波器的设计,首先是要设计一个FIR低通滤波器,并让其通带为所希望的带通滤波器通带的1/2,然后利用下面的公式将设计的FIR低通滤波器的系数转换成FIR 带通滤波器的I,Q两路系数:

4.2 时变多普勒频移
短波航空移动信道的时变多普勒频移由电离层产生的多普勒频移与相对运动产生的多普勒频移两部分组成,实现框图如图5所示。

图5 时变多普勒频移的实现框图
飞行器相对运动带来的信号多普勒频移与飞行器的运动速度有关,且要受到飞行器最大飞行速度与加速度的限制。当航空飞行器飞行轨迹不确定时,信号的多普勒频移还与其机动频率[15]有关。本文根据机动频率的等级,给出了3种典型场景下的机动频率参考值,如表1所示。针对这3种典型场景对航空飞行器速度进行仿真,假设飞行器的最大加速度为80 m/s2,最大飞行速度为600 m/s,随机生成100 s的速度变化仿真结果如图6所示。从图中可以看出飞行器可以做各种不同类型的运动,且随着机动频率的提升,飞行器的运动状态越来越复杂,与理论相符,满足进一步的仿真需求。

表1 3种典型场景下参数参考值

图6 随机生成航空飞行器的飞行速度


4.3 多普勒扩展
Watterson模型的理论推导中已假设多普勒扩展的功率谱服从高斯分布。由于高斯白噪声的功率谱服从均匀分布,可以利用高斯滤波器对高斯白噪声进行滤波,得到具有高斯功率谱的噪声序列,再与输入信号相乘,从数字信号处理角度来看,两个信号在时域做乘法运算,相当于在频域做卷积运算,即可实现频谱扩展。
由于噪声采样频率很高会造成高斯滤波器阶数较大,从而增大系统计算量。为了降低计算量,需要采用低采样频率的噪声序列通过插值滤波达到与系统采样频率一致。
对短波航空移动信道仿真时,参考国际电信联盟对典型短波电离层反射信道的仿真参数[16]。另外,由于实际上产生多普勒频移的是在3~30 MHz,但是数字信号处理的过程往往是在基带中进行的,要进行下变频处理。这里分别对载波频率为6 MHz和15 MHz的信号进行仿真,仿真时假设输入信号为从高频下变频到载波频率为200 Hz的单音信号,3条路径的延时分别为无延时,1 ms, 2 ms,时变多普勒频移仿真参数参照4.2节,多普勒扩展分别为0.5 Hz, 1 Hz, 1.5 Hz ,信噪比为10 dB,信道的冲激响应如图7所示。
从图7可以观察到,在同一机动频率下的不同时刻的信号的衰落不一,信道是个典型的时变衰落信道,且伴随着机动频率的增加,信号失真也更加明显。在不同载波频率上信号也呈现出不同的衰落,信道也是频率选择性衰落信道。从理论上讲,飞行器机动频率的增加使得其速度和加速度变化得越快,从而导致额外的多普勒频移和扩展。为了便于观察信号在频域上的变化,这里对15MHz载波频率下3个典型机动频率下的信道进行仿真,信号的频谱如图8所示。在频域波形中,输出信号发生了频移和频谱扩展现象,与理论相符。随着机动率的提升,信号的衰落和频谱扩展增加,在高机动场景下,信号严重衰落,几乎淹没于噪声中。仿真结果验证了本文提出的短波航空移动信道模型仿真算法的可行性。
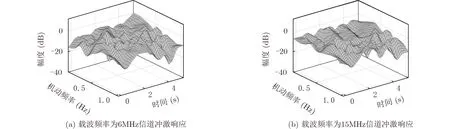
图7 短波航空移动信道的冲激响应

图8 3个典型场景下短波航空移动信道频谱图
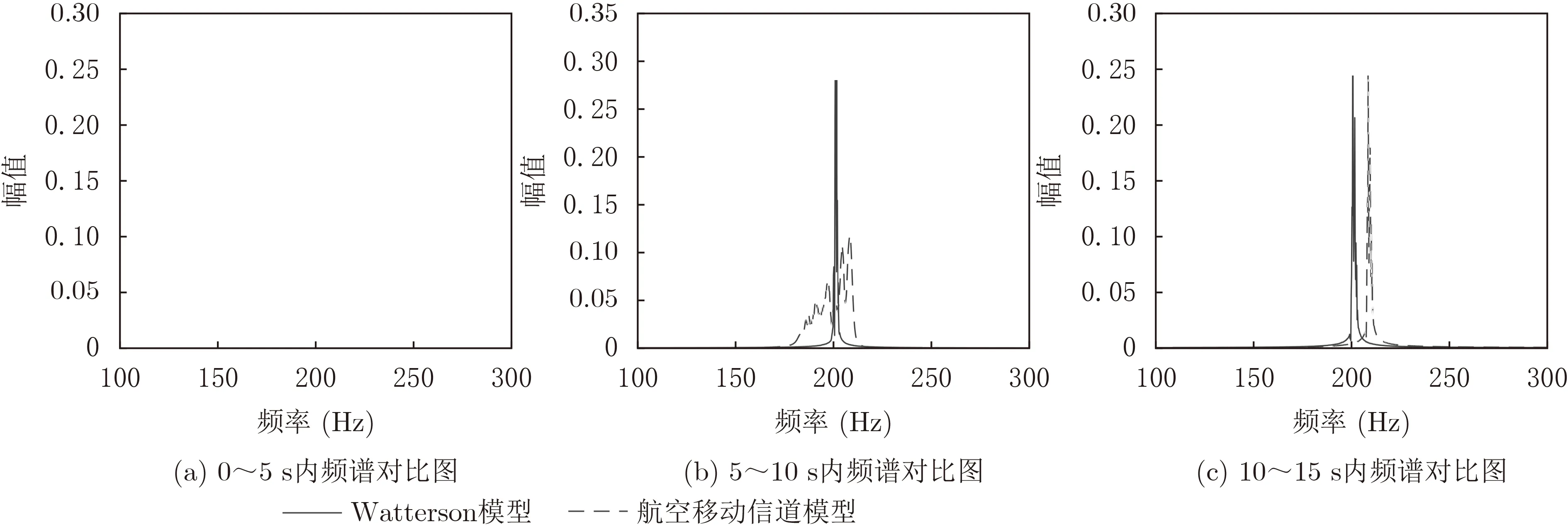
图9 不同运动状态下单路径Watterson模型与航空移动信道模型频谱对比
在民用航空领域,飞行器的飞行航线轨迹往往是确定的,当飞行器运动状态确定时,参照图2,运动参数如表2所示,其余仿真参数与上述仿真参数一致。为了便于观察每一种固定运动状态下多普勒频移和扩展的情况,这里取短波Watterson模型的一条径与短波航空移动信道的一条径在5 s内的频谱进行对比,如图9所示。从图中可以看出,在无噪声干扰的情况下,不同运动状态的频移和扩展差异很大。飞行器在直线运动下,与Watterson模型相比,信号整体发生了更大的频偏,且由于加速度影响,与匀速直线运动相比,匀加速状态下信号频谱扩展更大。飞行器在匀速圆周运动也伴随着运动方向的改变发生正向和负向频偏,与理论相符,进一步说明模型仿真的可行性。

表2 飞行器的飞行航线轨迹确定时运动参数
5 结束语
Watterson模型是当前短波信道模拟器所选用的通用模型,但对于短波超视距航空移动信道而言,收发两端处于相对运动状态,故还需考虑飞行器各种运动状态所带来的时变多普勒效应。本文先对Watterson信道模型进行理论推导,再通过分析航空飞行器的最大移动速度、加速度、机动频率、运动轨迹等机动状态参数对短波航空移动信道的影响,建立短波航空移动信道模型,该模型不仅能描述短波信道典型特征,还能有效描述由收发两端相对运动带来的多普勒频移和扩展。仿真结果表明,通过设置仿真参数,可以实现对不同机动频率下的短波航空移动信道仿真。当飞行器的飞行航线轨迹确定时,也能对特定飞行轨迹下的短波信道进行定制化仿真,对短波航空移动通信系统研究有重要的参考价值。
