古建筑木结构的承载及抗震机理

杨庆山

(重庆大学 土木工程学院，重庆 400044)

木结构是中国古建筑的主要结构形式，已延续了上千年，是中国传统文化的重要载体。古建筑在自然和人为侵害下，存在各类病害和残损，主要包括材质退化、节点与构件残损乃至整体性能劣化，其抗震安全问题尤为突出。

近30年来，众多学者[1-6]进行了古建筑木结构理论、试验等方面的研究，促进了古建筑保护的发展。但古旧木材劣化导致其强度难以准确定量；木构古建构造形制各异，节点类型繁多和缝隙广布、受力性能复杂；振动台试验表明其具有良好的抗震性能[5]，而拟静力试验却显示节点耗能能力低、构件弹性变形小[6-7]，这说明古建木构的承载和抗震机理尚未明晰揭示。

在国家自然科学基金重点项目的支持下，笔者与项目组成员一起开展了几个方面的工作：1)定量研究了木材材性劣化和构件强度退化机理；2)分析了柱脚节点承载能力和刚度变化对结构振动特征的影响；3)获取了榫卯缝隙特征，研究了考虑缝隙影响的榫卯节点力学性能；4)开展了斗栱受力性能的数值模拟，揭示了斗栱层协同作用机制；5)分析了木构架的摇摆特征、抗侧力机理和耗能机制。

1 古旧木材劣化

1.1 古旧木材性能

古旧木构件材性常因表面碳化、风雨和雪周期性侵蚀等导致有效承载截面减小，同时，由于长期荷载下的蠕变与损伤累积，导致古旧木材力学性能发生时变退化，引起木构件失效(见图1)。

图1 木构件的失效机理示意图Fig.1 Schematic diagram of failure mechanism

木材腐朽与木材细胞壁结构的变化有着不可分割的联系，细胞壁化学成分的降解能反映在其宏观力学性能上。木质素降解显著影响木材拉伸强度，综纤维素含量的降低明显降低了木材的抗弯强度，各化学组分在细胞壁中的存留方式均对其力学性能和保存程度产生影响。与完好木材(图2(a))相比，古旧木材具缘纹孔在不同程度上发生退化，具缘纹孔由于腐蚀导致开口扩大(图2(b))，裂纹通过具缘纹孔产生并呈对角线方向扩展到具缘纹孔周围的细胞壁(图2(c)、(d))[8]。通过这种方式可以从根本上认知木材性能劣化，并为提出有针对性的保护措施奠定基础。

图2 完好及古旧木材样品SEM图[8]Fig.2 SEM images of good and aged

在已有研究中，基于材性力学试验的古木材性能数据均具有离散性较大、相关性不强的现象[9-12]。为此，根据木材的胞体特征及承载情况，建立了可以考虑古木材性时变性能的古木构件强度退化模型[13]，强度退化随时间变化关系如式(1)所示。

(1)

式中：B为通过试验拟合出的累积损伤模型中的参数[14]；α(t)为木构件的损伤随时间变化的函数，其取值范围为[0,1]，当α=0时，表示构件无损伤，当α=1时，表示构件破坏；C0为基准年t0时的构件强度校正因子。

据式(1)可以得到木构件残余强度预测结果，该结果可以作为评估古建木构力学强度指标的参考值(图3)。将上述时变模型应用于西藏某典型古建筑木结构分析，获得其梁、柱构件服役寿命的均值分别为366、355 a，符合试验所用旧材为已经服役350 a后出现问题而被维修替换下来的实际情况(图4)。研究结果还表明，木构件所受的应力比越大，残余强度随时间变化的退化速率就越快，大部分情况下木构件是因蠕变导致的变形过大而发生破坏，而此时木材的强度并没有完全丧失[15-16]。

图3 古木构件残余强度比的退化规律Fig.3 Degradation law of residual strength ratio of

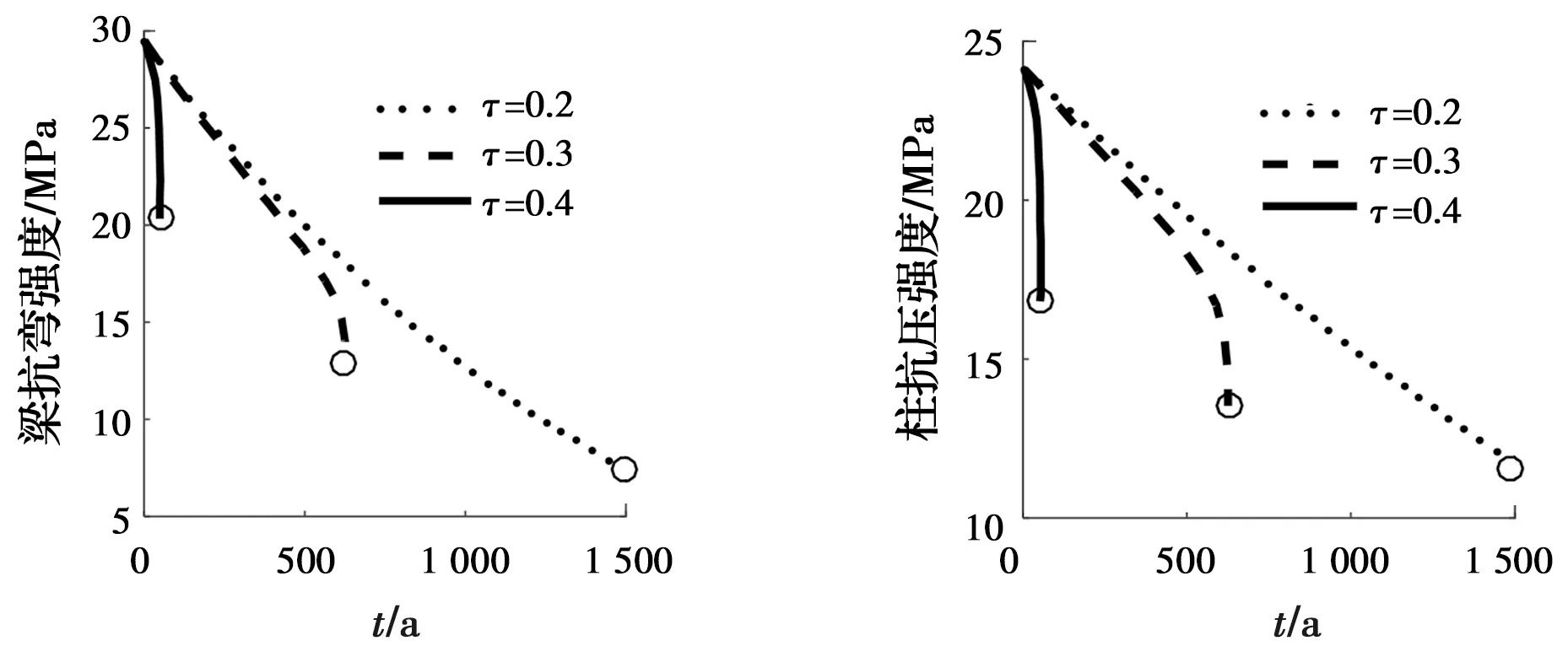
图4 梁、柱强度退化时变模型Fig.4 The time-varying model of strength degradation

1.2 古旧试件性能

目前，标准试验均采用清材[9,17-18]，且在统计的文献中大约有一半的情况古旧木材的强度大于新木材的强度[19]，不能反映古木构件的实际性能。这是由于木材心材与边材力学性能有差异，对木材横截面沿径向不同位置截取的小试样，其物理力学性质变化情况不同。

为了更加准确地反映古建木构件的强度，通过测试带缺陷小试件的强度，并结合统计学方法来评估古旧木构件的强度性能，同时，分析了抗压强度比γσ与古建筑年限t、带缺陷小试件相对圆心的取样位置λ(图5)的相关性，如图6(a)所示。根据已有试验数据拟合的关系如图6(b)所示，该结果随着古木材试件的增多可不断精细化[19]。

图5 取样位置

图6 抗压强度比与服务年限和取样位置的关系示意图Fig.6 Schematic diagram of the relationship among the compressive strength ratio, age of the timber member and

2 柱脚节点

古建筑木柱浮搁础石上，传递竖向和水平荷载但不承受轴向拉力，明显区别于现代结构的柱与基础的连接方式；水平荷载反复作用下，柱脚会发生转动导致木柱出现左右摇摆和抬升是古建筑木结构的明显构造特征。木柱转角较小时，柱脚与础石的接触部位较广，其初始转动刚度最大；随着转角增大，柱脚受压面由全截面受压变为部分截面受压，支持力作用点由柱底中心向柱脚边缘偏移，恢复弯矩增加，当柱脚受压面集中在柱脚边缘时，受压面的变化不再引起恢复弯矩的增加，转动刚度逐渐降低(图7)[20-23]。同时，在柱摇摆过程中，柱脚残余变形也能引起转动刚度的降低。

图7 柱脚节点拟静力试验Fig.7 Quasi-static test for column foot

针对柱脚在水平荷载作用下的运动状态，提出通过梁单元刚度K1、转动弹簧单元刚度K2[24]和几何刚度K3模拟木柱摇摆行为的方法，如式(2)和图8所示。

K=K1+K2+K3

(2)

图8 木柱的有限元模拟方法Fig.8 Finite element simulation method of wooden

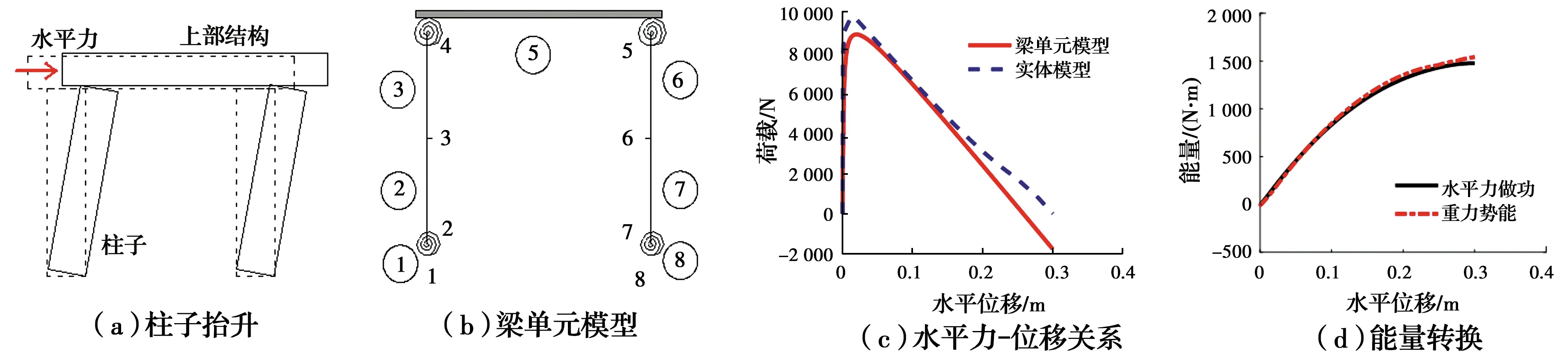
图9 柱脚抬升的能量转换机理Fig.9 Energy conversion mechanism when column foot

3 榫卯节点

榫卯节点是古建木构梁柱之间典型的连接方式，是中国古建木构中最显著的特征之一。榫卯节点的受力性能对柱架层甚至整体结构有重要的影响，其破坏会导致木构倾斜甚至整体倒塌。此外，由于榫卯节点构造初始误差以及长久服役过程中遭受自然灾害和木材干缩、徐变、腐蚀、塑性变形等影响，榫头和卯口之间普遍存在缝隙，显著影响结构变形、承载及服役性能，在古建筑木构结构分析时应作为一个主要参数对待。统计调查是获得榫卯缝隙特征的基本手段。

3.1 榫卯缝隙统计特征

以传统木结构中使用最广且研究最多的直榫和燕尾榫为对象，通过榫卯间缝隙(图10(a))大量样本采集，现场量测共获取5组总计1 478个缝隙值，包括古建筑直榫、燕尾榫水平方向、竖直方向缝隙值[25]。5组缝隙值的频率分布直方图均呈现相近的左偏态，筛选9种典型分布对5组缝隙值进行PPCC拟合优度检验，峰度、偏度计算结果接近的缝隙值均以Weibull分布最优。拟合的水平和竖向缝隙的概率密度函数如式(3)、式(4)所示。

(3)

(4)

其水平缝隙的频率分布直方图与Weibull分布概率密度函数曲线如图10(b)所示。建立的榫卯节点缝隙分布模型为榫卯模型的缝隙取值提供了重要参考。随着调查数据的不断丰富，缝隙统计模型精度也将不断提高。

图10 榫卯节点缝隙及水平缝隙的概率分布Fig.10 Gaps of mortise-tenon joints and distribution probability density function curve of horizontal

3.2 考虑缝隙的榫卯节点性能

图11 榫卯节点横纹受压过程Fig.11 Compressive deformation perpendicular to grain

图12 考虑缝隙影响的节点弯矩转角关系Fig.12 The effect of gaps on the relationship of

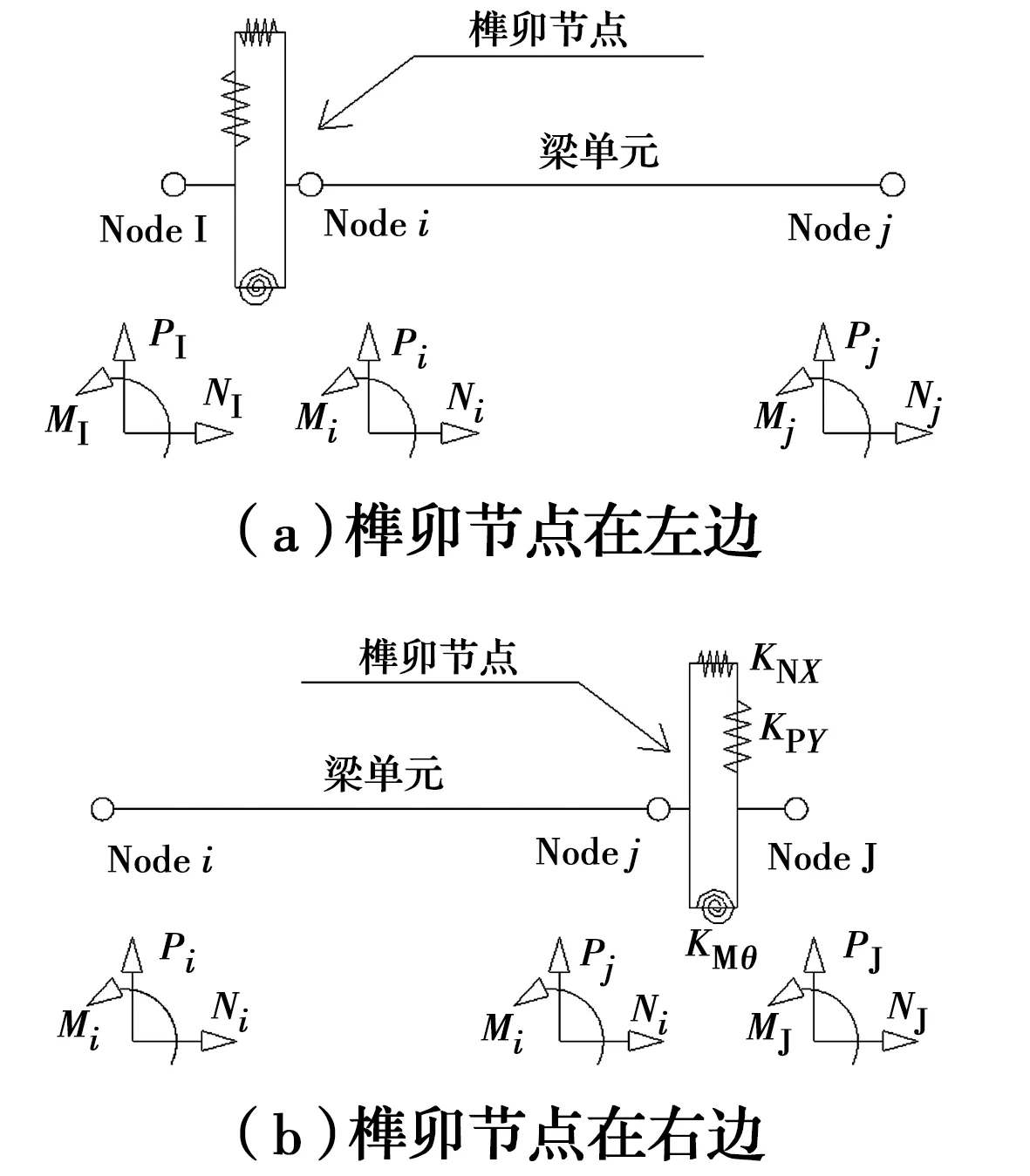
图13 包含榫卯节点的混合单元Fig.13 Hybrid finite elements including mortise-tenon

4 斗栱与铺作层

斗栱是中国传统建筑的特有构件，既能传递荷载，又具有装饰功能；与方桁共同构成斗栱层。不同学者通过试验研究或数值分析初探了其力学性能。

4.1 试验研究

在水平加载下，斗栱变形表现为整体偏心受压转动和构件间相对滑移的组合[27]，侧移刚度、转动刚度随竖向荷载的增大而增大。随水平荷载的多次重复，斗栱的加、卸载刚度退化，水平荷载作用下其耗能量及耗能能力均随水平位移的增大而增大(图14)。斗栱中多构件的相互挤压、嵌压、滑动摩擦等具有较好的耗能性能，体现于相对饱满的滞回曲线中。四朵斗栱模型的低周反复荷载试验(图15(a))结果表明[28]，模型的滞回曲线呈平行四边形(图15(b))，滞回面积饱满，说明斗栱层具有良好的耗能作用。

图14 单体斗栱拟静力加载试验及滞回曲线Fig.14 Static load test and hysteresis curve of

图15 四朵斗栱试验模型和滞回曲线[27]Fig.15 Test model of four Dou-gongs and hysteretic

4.2 理论分析

图16 实体单元模型与简化弹簧模型Fig.16 Solid element models and simplified

图17 斗栱模型的荷载位移曲线Fig.17 The load-displacement relationship of

两朵斗栱在水平荷载作用下的变形特征如图18所示，对比图18与图16(a)、(b)可知，在水平荷载作用下，单朵斗栱各层构件的相对转动方向一致；而两朵斗栱由于相互作用，其转动行为与单朵斗栱明显不同，下部构件的相对转动方向与上部构件的相对转动方向相反。同时，由图17可知，两朵斗栱模型在较大的荷载作用下只发生较小的位移，表明与单朵斗栱相比，两朵斗栱协同工作更类似刚体。由此可见，多朵斗栱的协调作用使得其与单朵斗栱的受力特征有较大的差别，因此，整个斗栱层的理论模型仍需要进一步研究。由于不同朝代斗栱构造差异较大，所以，有必要开展不同朝代斗栱层的理论模型研究。

图18 两朵斗栱各层间相对转动Fig.18 The relative rotation of two

5 木构架承载与抗震机理

古建筑木构架中柱脚和榫卯的协同作用的使得木构架主要呈现摇摆的运动特征。含梁柱及斗栱的古建筑动力及拟静力试验表明[29-31]，木结构的恢复力在变形较小时主要来自柱摇摆，随着结构水平变形的增大，榫卯节点的作用越来越显著；竖向荷载明显影响柱摇摆的恢复力，柱以上构件类似刚体运动。

5.1 木构架抗侧力试验

按《营造法式》制作了含梁柱构架和斗栱层的木结构1∶2缩尺模型[32]和对应的足尺模型拟静力试验(图19)[33]。随着水平荷载的增加，柱脚一侧逐渐抬升，柱头产生明显偏压，水平变形集中于柱的倾斜，斗栱层近乎刚体在平动；卸载过程中构架逐渐自动复位，各部位无明显残留变形。

图19 木构架拟静力试验Fig.19 Quasi-static test device for wooden

与斗栱饱满的滞回曲线不同，木构架的滞回曲线呈现狭长带状的S形(图20(a))，整体结构耗能能力弱；但木构架最大层间位移角达1/22后，仍能自行恢复到接近初始位置，表现出很强的变形能力；木构架侧移刚度随竖向荷载的增大而增大、随水平位移的增大而减小；相同竖向荷载工况下，前后两次加载过程中木构架侧向刚度下降幅度可达36%(图20(b))。

图20 木构架的滞回曲线和刚度退化Fig.20 Hysteresis curves and degradation of

木构架在水平荷载作用下会产生竖向位移，即柱头及以上结构抬升明显(图21(a))。水平荷载输入木结构中的能量转化为弹性应变能、滞回耗能和屋盖抬升获得的重力势能。变形初期，输入的能量主要转化为滞回耗能和弹性应变能；当水平位移较大时，总输入能量的50%将转化为重力势能(图21(b))。这种能量转化机制可使输入到结构中的地震能量得到缓慢释放和消耗，减小构件损坏，是古建筑木结构耗能能力弱但抗震性能好的重要原因[6-7]。

图21 竖向抬升和重力势能占比Fig.21 The uplift of roof and proportion of gravitational

5.2 构架摇摆性能的理论分析

通过对柱脚节点、榫卯节点和斗栱构件的组装，可以建立木构架的摇摆分析模型，如图22所示。关键节点部位采用弹簧单元模型模拟，其他部分则使用梁单元来模拟，并采用MATLAB自编程序进行建模分析。

图22 摇摆构架模型Fig.22 The model of rocking

在地震作用下，弹性阶段木构摇摆过程中的能量如式(5)所示。

EK+ED+EG+EE=EI

(5)

式中：EK、ED、EG、EE和EI分别为动能、阻尼耗能(包括摩擦耗能)、重力势能、弹性应变能和地震输入能量。

木构架摇摆过程中地震输入的能量主要转化为阻尼耗能ED、重力势能EG和动能EK(图23)。往复摇摆下重力势能EG和动能EK相互转换，但地震输入的能量不断并最终转化为不可恢复的阻尼和摩擦耗能ED(图24)。古建木构包含成百上千个榫卯节点，且各层叠的木枋之间均存在摩擦耗能，使得摩擦耗能具有“量大、面广”的特征，分析较为复杂，因此，木构摇摆过程中的耗能评估仍需细化研究。

图23 木构架摇摆过程中能量分析Fig.23 Energy analysis of the wooden frame

图24 地震作用下古建木构的能量传递Fig.24 Energy transfer of traditional wooden structure

6 结论

基于材性评估，节点、构件及结构受力特征分析，在古建筑木结构的基础研究方面得到了如下结论：

1)建立了可考虑古木时变特征的材性及构件强度退化模型。

3)建立了古建木构摇摆体系动力分析理论，揭示了节点摩擦耗能、重屋盖高位储能、构架长周期摇摆释能的古建木构抗震机理。

(致谢：感谢国家自然科学基金重点项目组成员北京交通大学杨娜、王娟，太原理工大学李铁英、魏剑伟对本文的贡献。)