基于LSTM神经网络的多源数据融合桥梁变形重构方法
2022-02-24张立奎段大猷王佐才
张立奎,段大猷,王佐才
(1. 安徽省交通控股集团有限公司,合肥 230088;2.合肥工业大学 a.土木与水利工程学院;b.安徽省基础设施安全检测与监测工程实验室;c.土木工程防灾减灾安徽省工程技术研究中心,合肥230009)
桥梁的位移是桥梁健康监测中的重要参数,可以直接反映桥梁的变形及运营状态。在工程中,通常采用水准测量系统直接测量位移,但这种方法难以长期监测位移且测量频率低。其他的位移直接测量方法,如线性差动变压器(LVDT)、实时动态差分全球定位系统(RTK-GPS)[1]、激光多普勒振动仪(LDV)[2]、雷达传感器[3]、激光雷达(LiDAR)[4]、计算机视觉方法[5],存在设备成本高、采样率低、适用性有限等缺点。对于间接测量法,倾角仪挠曲重构法的测量精度相对较低,而且用倾角仪进行动挠度测量时,对各倾角仪的相位差、瞬态反应以及零漂等有着较高的要求[6]。近年来,应变的测量精度获得了较大提高,特别是分布式光纤光栅传感技术的应用,可以实现桥梁应变的分布式监测,故基于应变的挠度测量方法获得较广泛的应用[7-9]。
对于实际桥梁的复杂结构,难以准确地获得桥梁的边界条件及模态振型,产生的误差可能影响最终变形重构的精度。Moon等[15]提出了一种基于BP神经网络和桥梁纵向应变的实时桥梁挠度重构方法。Tian等[16]使用双向LSTM神经网络构建了斜拉桥索力监测数据与主梁挠度的关系模型。LSTM作为一种循环神经网络(RNN)体系结构被广泛应用于时间序列建模中[17-19],也可以应用于基于监测数据的变形监测。笔者建立了多层堆叠LSTM神经网络,通过数据训练建立应变、加速度监测数据与桥梁变形的关系,实现了数据融合,变形重构在数值模拟及试验验证中获得良好的结果,具有较高的精度。
1 多源数据融合LSTM神经网络
1.1 LSTM算法原理
LSTM神经网络具有长时间记忆信息的特性,不仅可以从单个数据点提取信息,还可以从整个系列数据中提取信息。LSTM神经网络允许信息持久化循环,其结构由元胞序列构成。神经网络的元胞结构如图1所示,xt是时间序列的输入,ht是时间序列的输出,t表示时间。
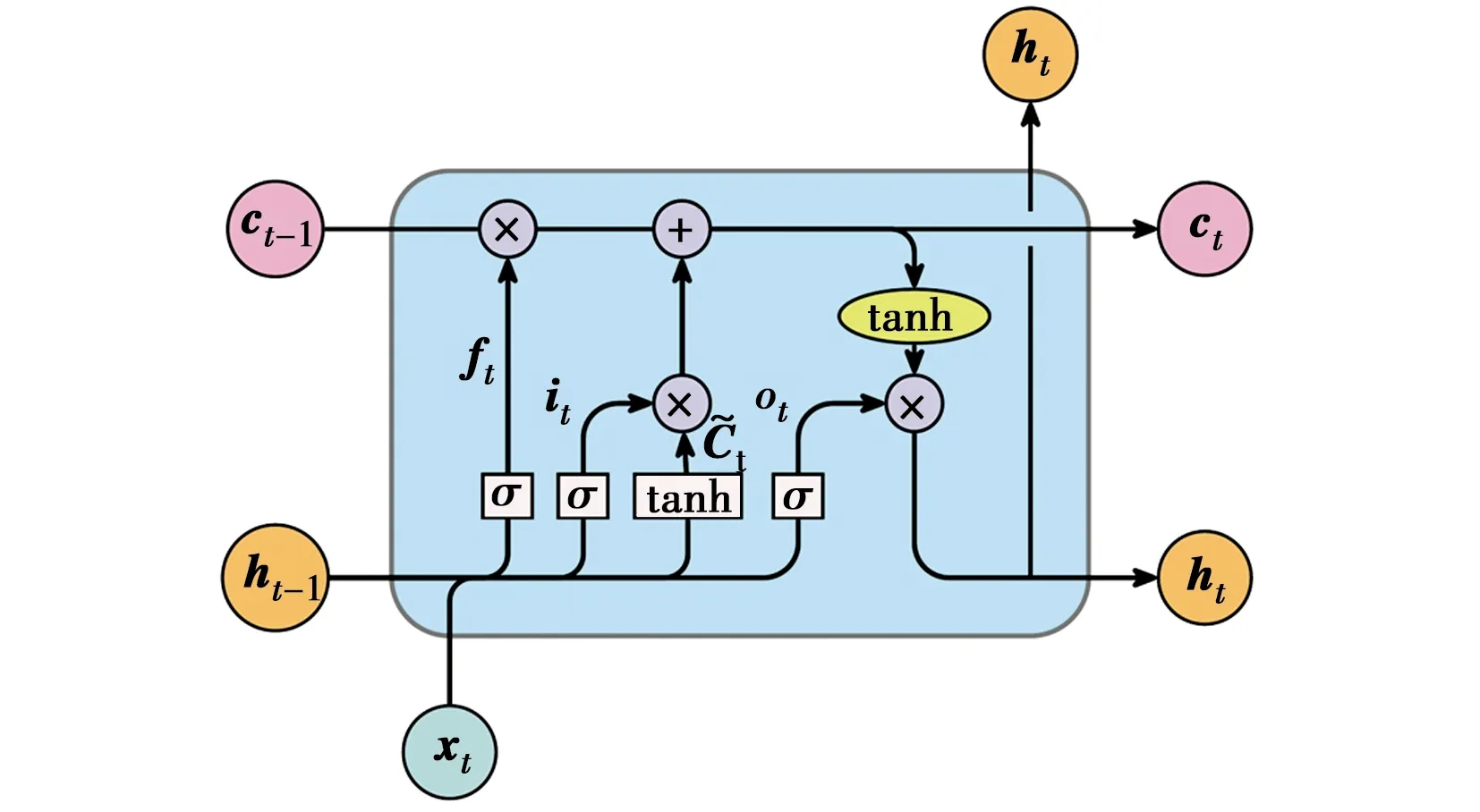
图1 LSTM元胞的结构
在LSTM单元中,函数σ和tanh表示为
(1)
(2)
神经网络元胞中有3种门:遗忘门、输入门和输出门。遗忘门通过式(3)决定需要保留多少Ct-1状态参数;输入门使用式(4)和式(5)确定保存到Ct的输入;输出门通过式(6)~式(8)控制输出。
ft=σ(Wf·[ht-1,xt]+bf)
(3)
it=σ(Wi·[ht-1,xt]+bi)
(4)
(5)
ot=σ(Wo[ht-1,xt]+bo)
(6)
ht=ot*tanh(Ct)
(7)
(8)
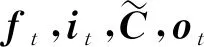
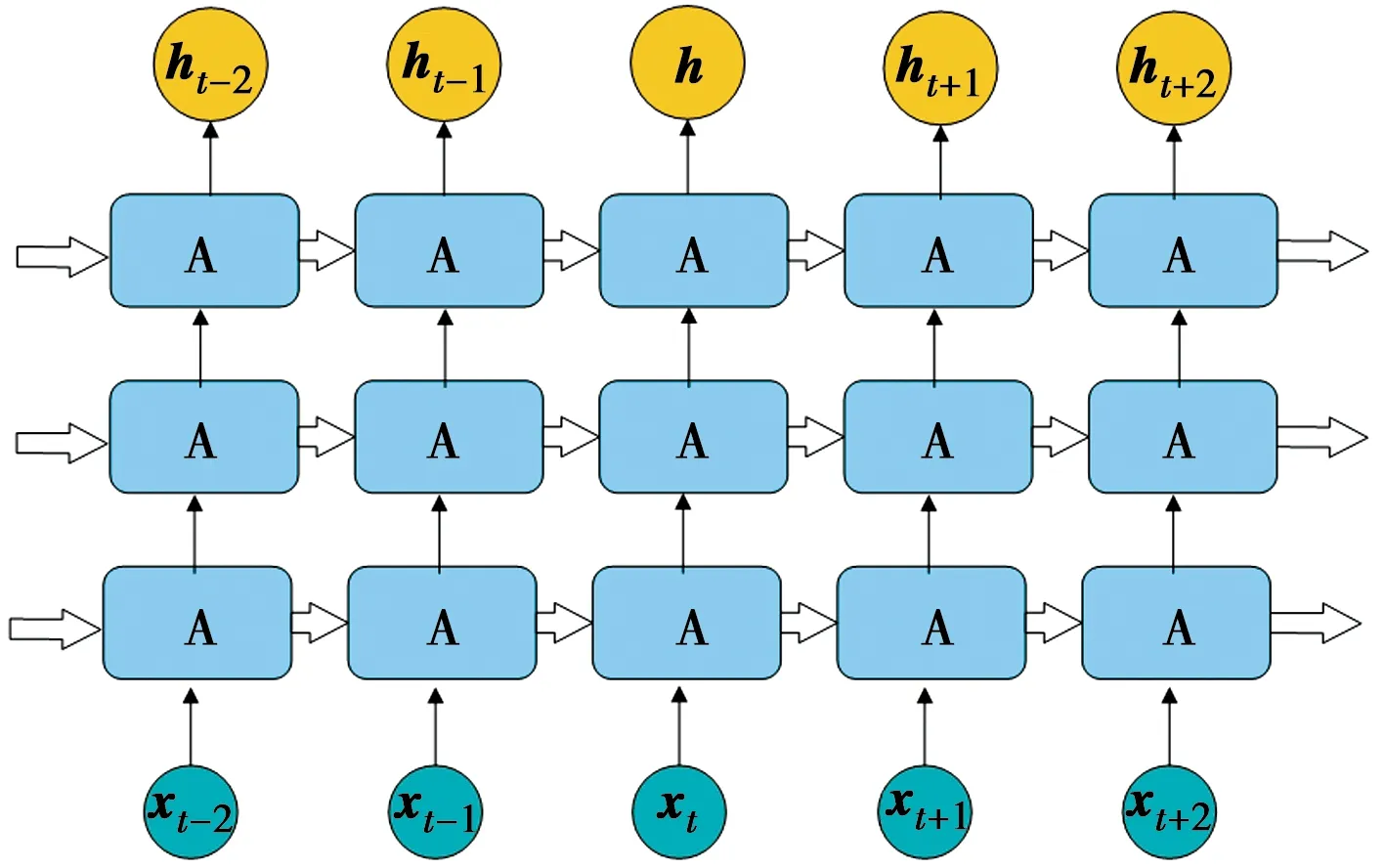
图2 堆叠LSTM神经网络结构
1.2 LSTM神经网络重构变形流程
多源数据融合变形重构方法流程示意图如图3所示。首先对应变和加速度的原始数据进行预处理,采样频率与加速度一致的应变数据可以直接作为神经网络的输入,对低采样频率的应变数据进行三次样条插值至与加速度数据采样频率一致。
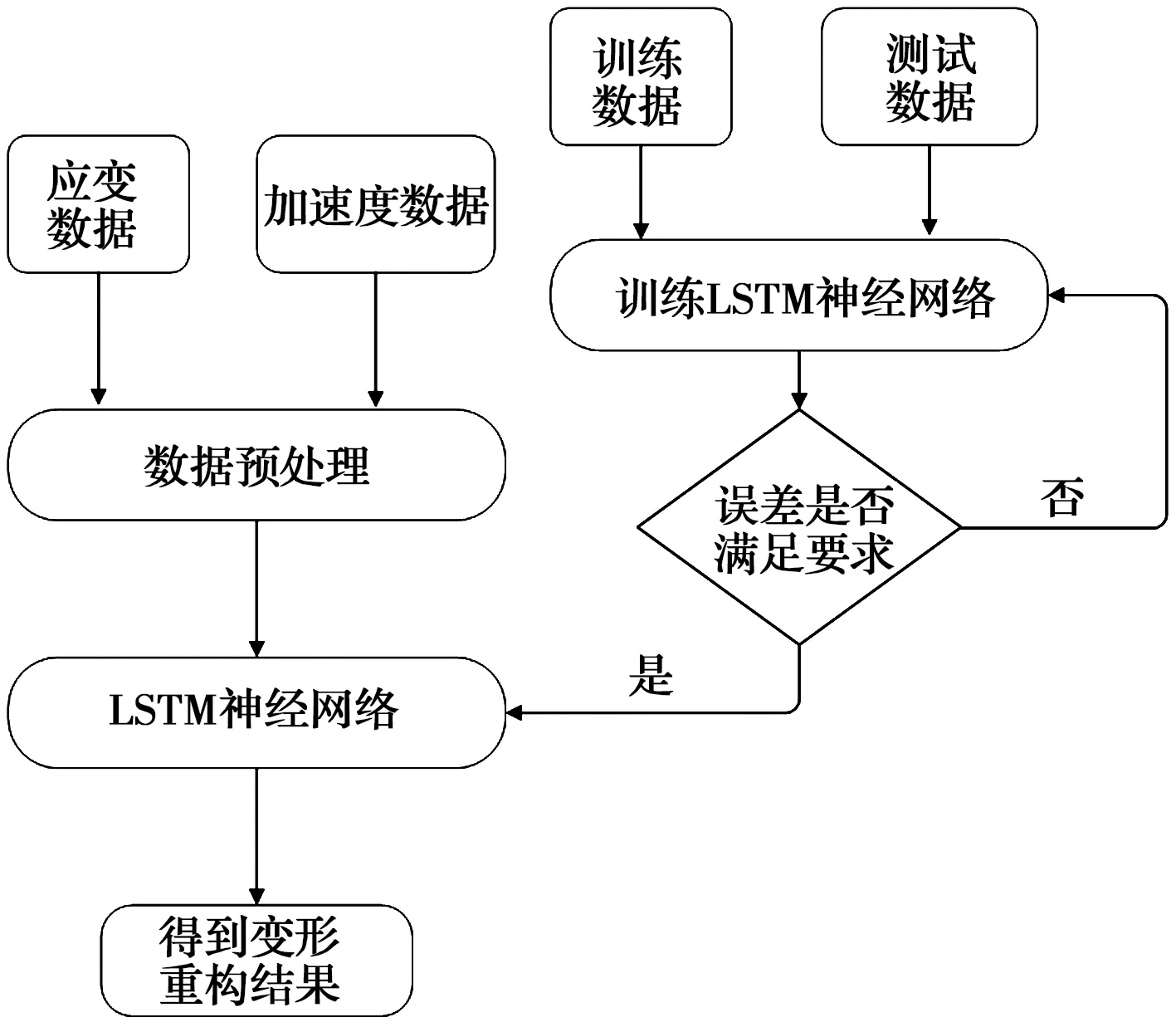
图3 桥梁变形重构流程
由于输入原始加速度数据后神经网络的变形重构精度不理想,为保证重构变形的高频精度,对加速度数据进行预处理。对加速度二次积分并通过FIR滤波器去除积分过程中产生的低频漂移现象,将预处理后的数据作为神经网络的输入数据。通过有限元模拟或者实际测量获得神经网络训练数据,经过训练获得LSTM神经网络。实际应用中,将预处理之后的数据输入训练好的堆叠LSTM神经网络中,即可获得桥梁的变形位移。
2 数值模拟
2.1 有限元模型
使用有限元模拟软件建立桥梁动态车桥耦合系统的有限元模型。该桥为混凝土桥面、工字钢主梁4跨连续梁桥,每跨35 m。混凝土桥面厚度为0.22 m,杨氏模量为34.5 GPa,泊松比为0.2,密度为2 700 kg/m3。工字梁高1.8 m,截面面积为854.4 cm2,上翼缘宽度为800 mm,下翼缘宽度为960 mm。工字钢梁的杨氏模量为206 GPa,泊松比为0.28,密度为7 850 kg/m3。车辆为具有二次悬挂的55 t卡车。桥梁整体如图4所示,桥梁横截面如图5所示。桥面铺装的不平整度为国家标准GB/T 920—2002中规定的c类。

图4 桥梁有限元模型
图5 桥梁模型横截面
选取一侧主梁对该方法进行验证,通过有限元法获得主梁测点处的应变、加速度和位移。应变、加速度和位移的采样率均为100 Hz,对数值计算获得的应变和加速度数据添加5%的高斯白噪声以模拟实际测量的误差。测量点的布置如图6所示。

图6 测点分布图
2.2 神经网络训练
通过有限元车桥耦合系统模拟获得神经网络的训练数据。训练数据包括一辆卡车以50 km/h和80 km/h的速度行驶通过桥梁,以及多辆卡车以50 km/h的速度通过桥梁。
在LSTM神经网络的训练中,较大的批量(batch size)通常导致更快的模型收敛,但可能最终收敛不佳;较小的批量会导致训练过程波动较大。基于Bengio[18]的研究,大于10的批量计算速度较快,本文使用的神经网络训练批次大小设为32。选取激活函数时,由于Sigmoid函数容易产生梯度消失,Relu函数可能导致训练过程中梯度归零的问题,因此,激活函数选用Tanh函数。优化算法为Adam,该算法对每个配置参数使用最佳实践初始值,适用于各种问题。当dropout参数为0时,神经网络训练出现了过拟合;当dropout参数设为0.3时,神经网络开始欠拟合。为了使LSTM达到最佳精度,使用正则化方法将dropout参数设为0.2。
为了选择合适的隐藏层数,图7比较了不同隐藏层的堆叠LSTM神经网络的训练损失,训练的遗忘率都设为0.2。均方误差(Mean Squared Error, MSE)表示在训练堆叠LSTM网络时每个时间步的训练损失。训练损失可以表示为
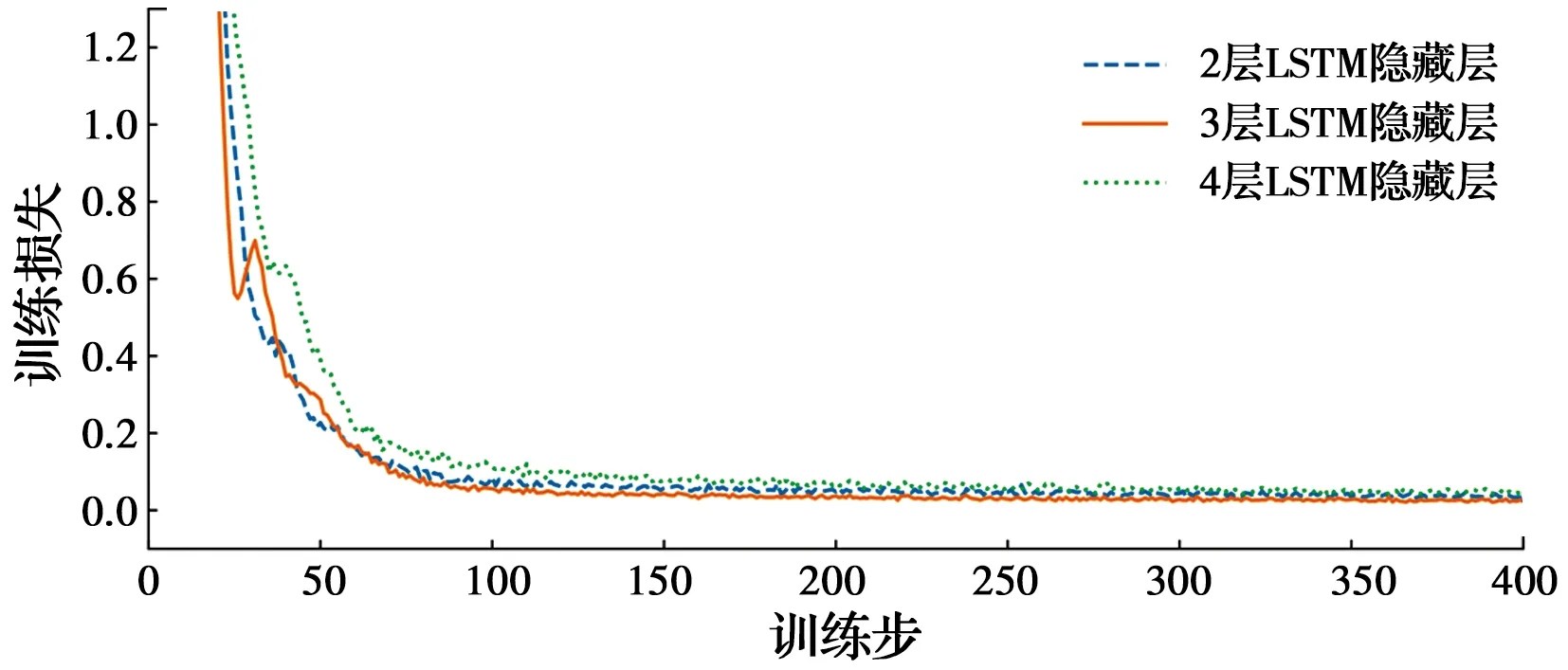
图7 不同层数LSTM神经网络的训练损失
(9)
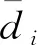
2.3 变形重构结果
经过训练的神经网络可以完成对桥梁变形的重构,对基于加速度的FIR滤波器[19]、基于应变模态[10]以及LSTM数据融合的变形重构方法结果进行对比。本例中,3辆载重55 t的卡车以60 km/h的速度通过桥梁,卡车之间的距离是35 m。重构位移与实际位移的对比如图8所示。
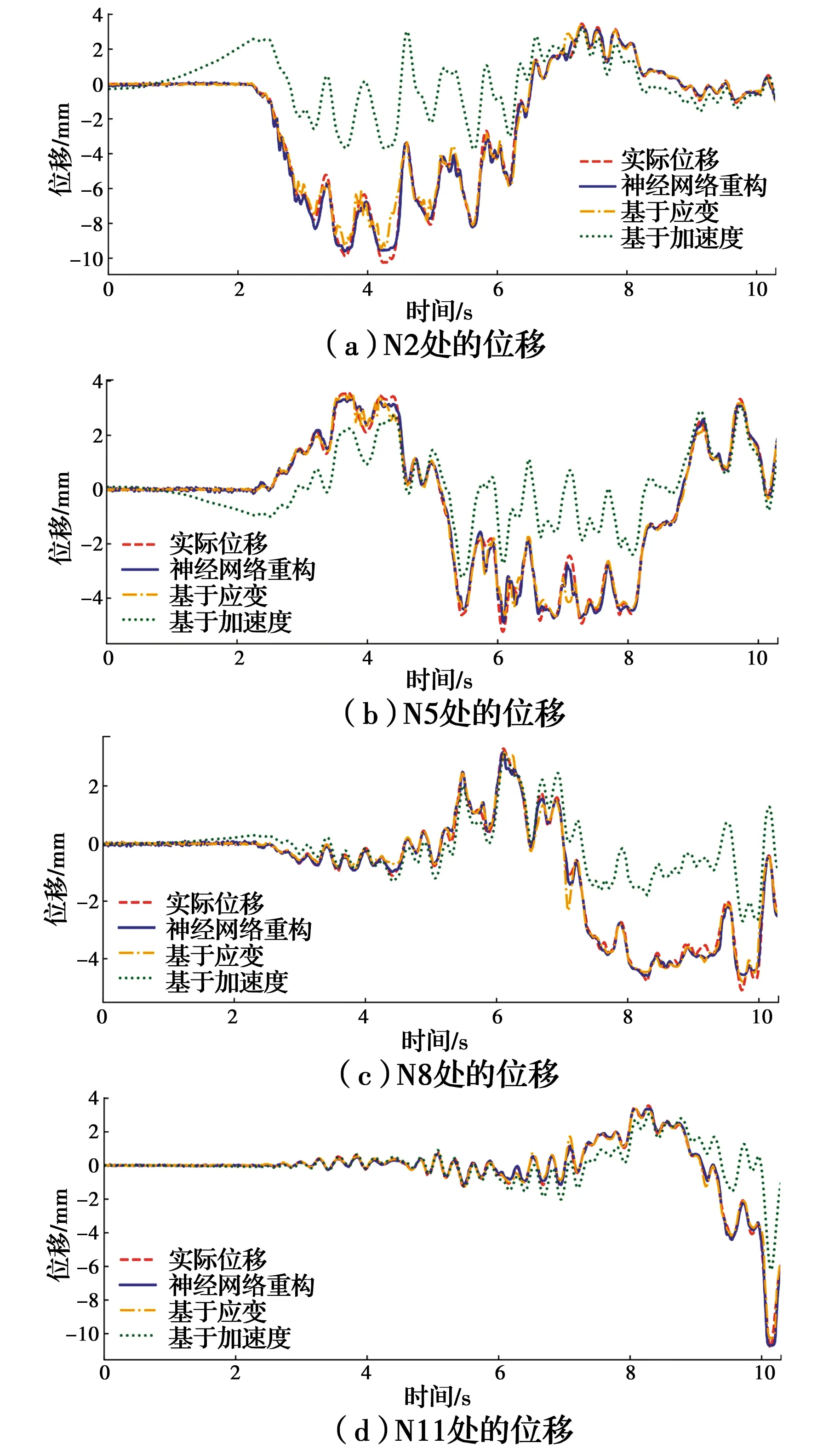
图8 位移重构结果对比
各个测点的重构位移误差如表1所示,提出的方法在多车荷载情况下具有较高的准确性,误差最大不超过7.5%。而基于加速度的位移重构方法,FIR滤波器消除了输入数据的低频信息,避免了低频漂移,但也因此导致位移重构误差较大。与基于应变的方法相比,提出的LSTM神经网络变形重构方法增加了加速度数据,提高了变形重构的精度。经过简单的训练,堆叠LSTM神经网络即可完成数据融合并构建测量数据与变形的关系,结果表明,该方法可以获得更高的精度。
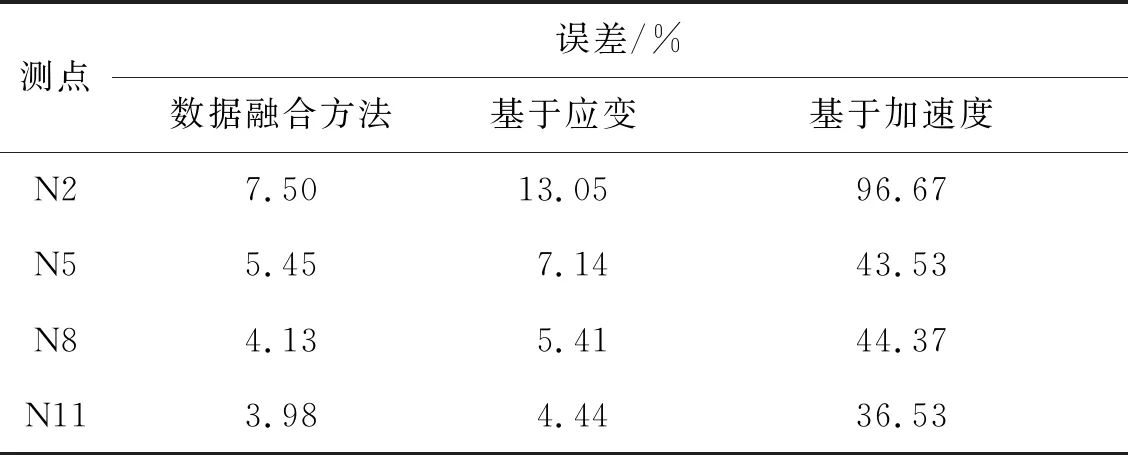
表1 各测点的误差
3 试验验证
3.1 试验概况
为了进一步验证利用应变和加速度数据融合的位移重构方法,对不同边界条件的梁进行试验。试验梁为长2.8 m的铝梁,宽度为100 mm,厚度为20 mm,弹性模量为70 GPa,泊松比为0.33,梁的密度为2 700 kg/m3。试验验证了简支梁和连续梁的工况。
简支梁表面均匀放置7个应变传感器,间距为35 cm。在1/4、1/2和3/4跨距处安装加速度传感器和电涡流位移传感器。对于两跨连续梁,去除了梁中点处的传感器,其余传感器的布置与简支梁相同。简支梁和两跨连续梁的传感器布置如图9所示,整体布置和信号采集系统如图10所示。在采样频率为200 Hz的情况下,测量了应变、加速度和位移。
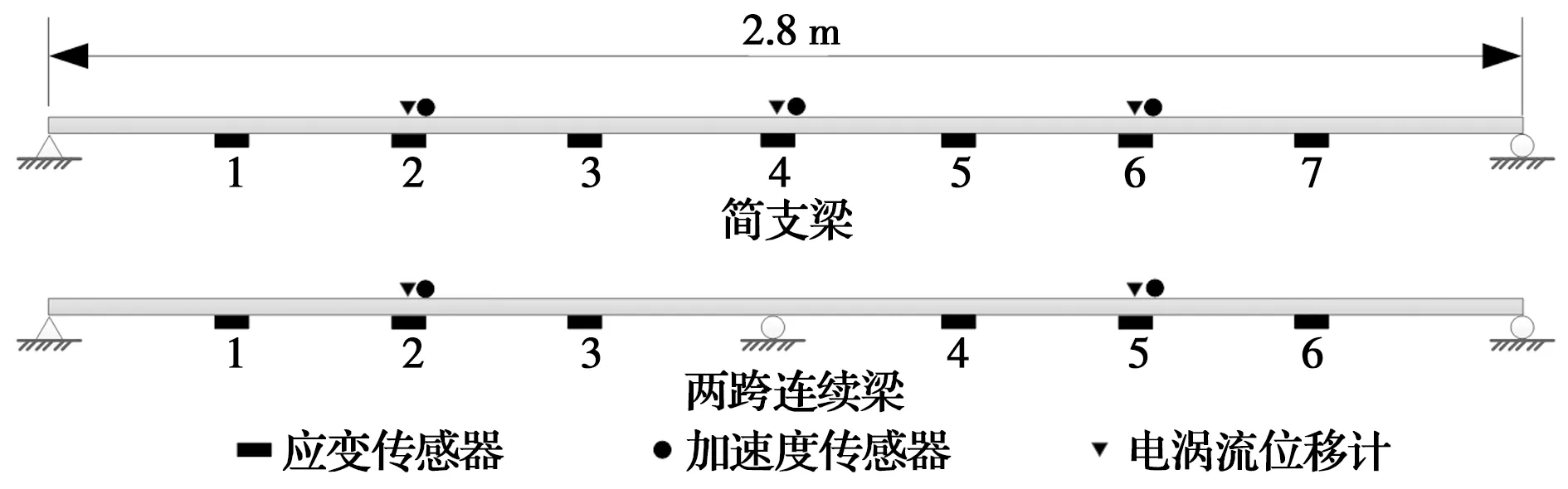
图9 传感器布置示意图

图10 试验梁和数字采集系统
3.2 试验结果
在变形重构前需要对LSTM神经网络进行训练,使用的LSTM神经网络结构以及相关参数与2.2节一致。
3.2.1 简支梁 对试验梁施加随机锤击激励,先通过20 s数据对LSTM神经网络进行训练。训练后的神经网络即可重构目标点的位移,位移重构结果如图11所示。
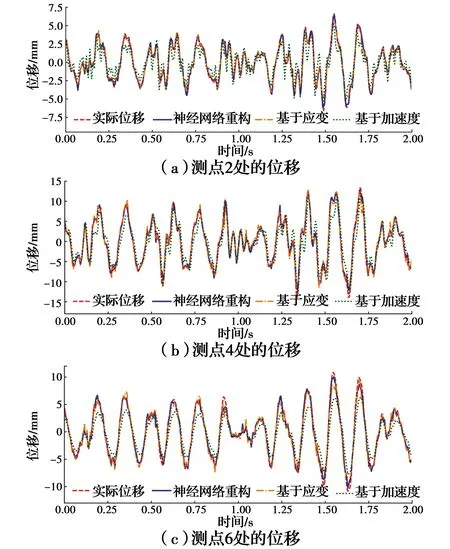
图11 简支梁重构位移对比
为了深入分析变形重构结果,每2 s对试验结果计算一次误差,误差函数定义为
(10)
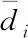

图12 简支梁各测点变形重构误差
3.2.2 连续梁 对连续梁施加随机锤击激励,位移对比如图13所示。基于数据融合的LSTM变形重构方法结果,每2 s的误差如图14所示。
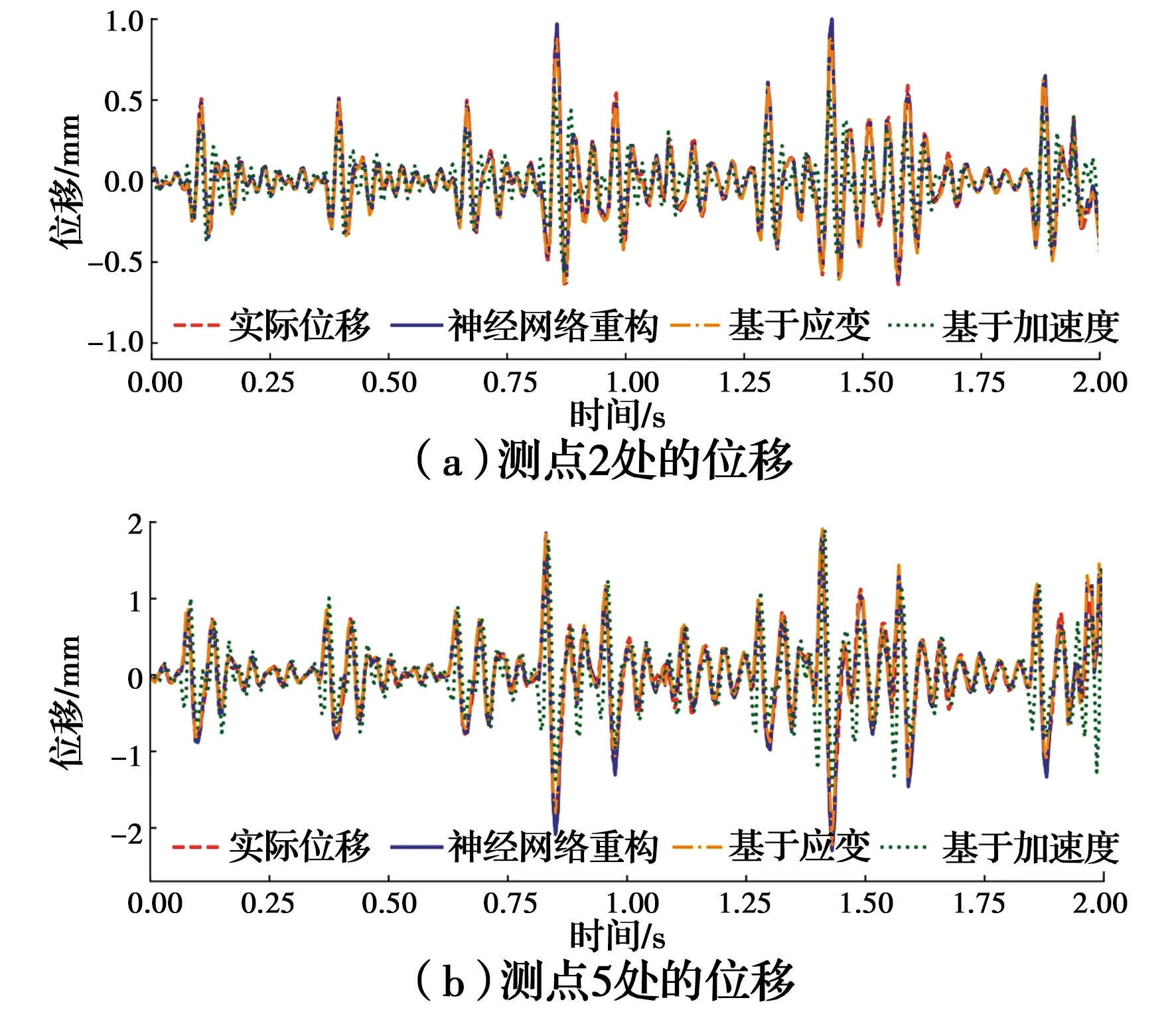
图13 连续梁重构位移对比
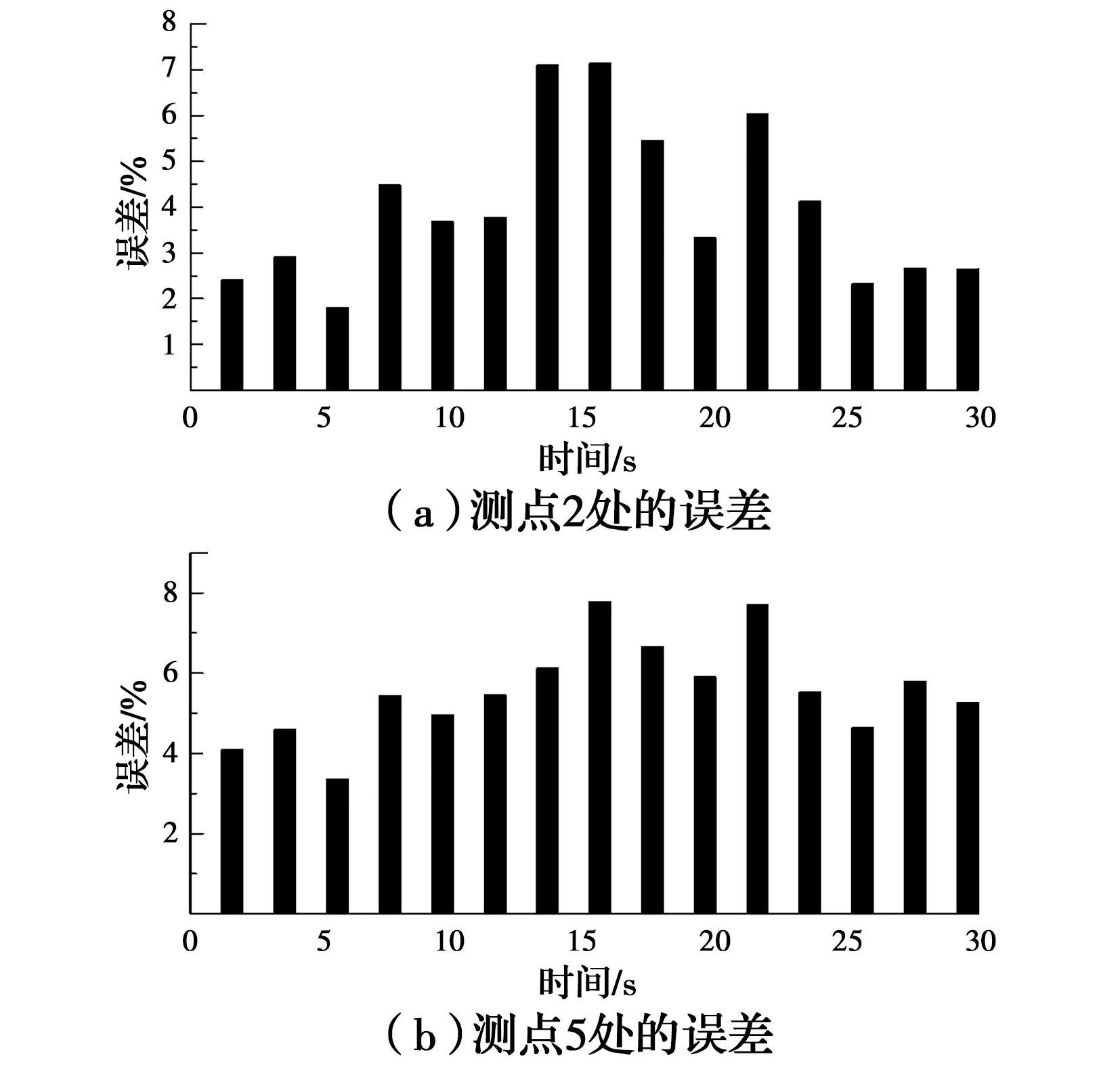
图14 连续梁各测点变形重构误差
数据融合的LSTM变形重构方法最大误差小于8%,堆叠LSTM网络在不同情况下均性能稳定。相比之下,基于应变和基于加速度的变形重构方法误差高于LSTM神经网络变形重构方法。
4 结论
提出了一种基于LSTM神经网络的多源数据融合变形重构方法。该方法可以将实测加速度和应变数据融合,实现高精度的位移重构。其主要优点包括:
1)提出的基于堆叠LSTM网络的位移重构方法,数据经过简单预处理后即可输入神经网络,数据融合过程由网络自动完成。
2)经过简单的训练后,LSTM网络可以准确地重构不同工况下的位移。在位移重构过程中,不需要预先知道结构的中性轴和模态振型。
3)经过训练的堆叠LSTM神经网络可以自动融合不同类型的测量数据,位移重构精度比基于单一源的方法更准确。
