基于粗糙集约简与狮群优化算法的机器人路径规划研究

2022-02-24万仁霞高艳龙

郑州大学学报（理学版） 2022年2期

万仁霞，高艳龙

(宁夏智能信息与大数据处理重点实验室宁夏银川 750021)

0 引言

机器人是一种能够半自动或全自动工作的智能机器，已经广泛应用于现代农业、仓库物流、医疗、航天、军事等领域[1-3]。路径规划是指移动机器人在有障碍的环境中选取一条从起点到终点的行走路线，要求路径最短且能安全、无碰地通过障碍物[4]。目前，国内外学者在机器人路径规划上进行了大量的研究，主要分为静态的路径规划和动态的路径规划[5]。传统的机器人路径规划算法有A*算法[6]、人工势场法、栅格法[7]和自由空间法[8]。

智能算法由于其杰出的寻优能力而应用在机器人路径规划研究中。例如，文献[9]对蚁群算法在机器人路径规划中的应用进行了分析和对比；文献[10]使用斥力场下粒子群算法对移动机器人在复杂环境下进行路径规划；文献[11]综述了遗传算法在机器人路径规划中的应用；文献[12]利用具有速度变异的粒子群算法优化微型足球机器人运动的路径；文献[13]将随机编码的交叉算子引入粒子群算法中，解决机器人最佳路径规划问题。针对机器人路径规划时种群规模大、冗余数据多、易陷入局部最优以及收敛速度慢等问题，本文提出一种基于狮群优化算法和粗糙集约简技术的机器人路径规划算法。其中，狮群优化算法具有收敛速度快、精度高以及较好的全局寻优性等优点；粗糙集约简技术可以提高机器人的全局路径规划能力和时间效率，从而有效地对机器人的行走路线进行规划。相比其他同类算法，本文算法具有更好的寻优质量和更快的收敛速度。

1 相关知识

1.1 狮群优化算法

狮群被分为狮王、雌狮和幼狮。狮王负责守护领地安全和给幼狮分配食物；雌狮负责捕猎和养育幼狮，在捕猎时与其他狮子相互协作；幼狮主要围绕在狮王和雌狮周围活动，幼狮活动分为三种情况：饥饿时向狮王靠近进食；吃饱后向雌狮靠近学习捕猎；有能力生存后被狮王赶出领地去锻炼。

1)狮群初始化

利用狮群优化算法(lion swarm optimization，LSO)[14]求解问题时，每个食物位置代表优化问题对应的一个可行解。位置的好坏由狮子个体的适应度值来判断，适应度值最好的代表狮王，适应度值最差的代表幼狮。随机生成含有N个解的初始狮子种群，空间维度为D，成年狮子占狮子总数的比例因子为β，成年狮子的数量为nLeader，

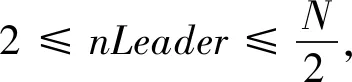
(1)

nLeader=「Nβ⎤，

(2)

其中：β为(0,1)的随机数。设狮子在寻优过程中的位置向量为xi=(xi1,xi2,…,xiD),1≤i≤N，寻优过程中不同类型狮子所处位置会按照自身方式来移动。

2)狮王守护领地

狮王在最佳食物处小范围移动以确保自己的特权，位置更新公式为

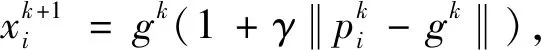
(3)

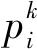
3)雌狮捕猎

狮王确定后，需要选择捕猎狮，雌狮在捕猎过程中需要跟另外一只雌狮协作，位置更新公式为

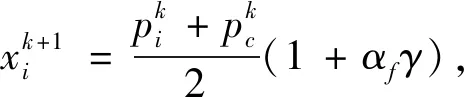
(4)

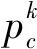
狮子在活动范围内移动的最大步长为

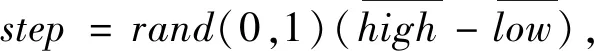
(5)

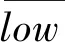
雌狮移动范围扰动因子可以表示为

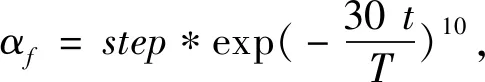
(6)

其中：T为群体最大迭代次数；t为当前迭代次数。

雌狮前期在较大范围内搜索食物，然后慢慢收缩搜索空间，后期保持搜索范围是趋于零的微小值。

4)幼狮跟随

幼狮的数量为N-nLeader，跟随狮王和雌狮活动，幼狮向狮王靠近或跟随雌狮学习捕猎过程中均在指定范围内移动。幼狮移动范围扰动因子可以表示为

(7)

幼狮先大范围搜索食物，发现食物后再仔细查找。第i只幼狮在捕猎范围内被狮王驱赶的位置可以表示为

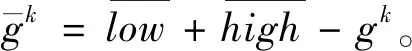
(8)

幼狮位置更新公式为

(9)

1.2 粗糙集约简

1)粗糙集理论

粗糙集借鉴了逻辑学中对不精确信息和模糊信息的各种定义，对知识库提出不精确范畴。粗糙集理论是概率论、模糊集、区间集之后一种新的软计算方法，在科学与工程领域得到了广泛应用[15]，是当前人工智能理论及其应用领域中的研究重点之一。

定义1[16]粗糙集由两个集合组成，给定的信息库K=(U,R)，令X⊆U，R为U的一个等价关系，定义X关于信息R的上、下近似集分别为

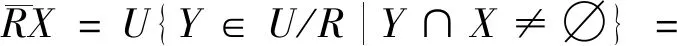
{x∈U|[x]R∩X≠∅}；

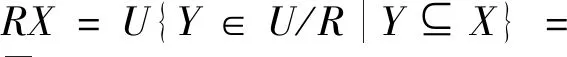
{x∈U|[x]R⊆X}。

2)知识表达系统

设U≠∅，研究对象的有限集合称为论域，U中的任何概念称为知识。知识表达系统由研究的对象组成，对象的信息通过其基本属性和属性值来描述。

定义2[17]设知识表达系统是一个四元组表示S=(U,A,V,F)，其中：U={x1,x2,…，x|U |}是非空有限的数据集合；A={a1,a2,…，a|A|}是非空有限集合，A=C∪D，C是条件属性，D是决策属性；V=∪Va，Va表示a∈A的值域；F:U×A→V是信息函数，∀x∈U，a∈A，F(x,a)∈V。

3)约简和核

知识(属性)约简和核是粗糙集理论的核心内容之一。知识库中并非所有的属性都是必要的，有些属性是冗余的。知识约简是在保持知识库分类能力不变的条件下，删除不重要或不相关的属性。完成知识约简涉及两个基本概念：约简和核。

定义3[17]R为一族等价关系，r∈R,若ind(R)=ind(R-{r})，称属性r在R中是不必要的，即冗余属性；否则，称属性r在R中是必要的，即重要属性。若每一个r∈R为R的重要属性，则称R是独立的，否则称R是依赖的。

定义4[17]设Q⊆P,若Q是独立的，ind(Q)=ind(P),称Q是P的一个约简。其中，P的所有的必要关系组成的集合称为P的核，记为core(P)，core(P)=∩red(P)，red(P)表示P的所有约简。

2 基于粗糙集约简与狮群优化算法的机器人路径规划

2.1 运动路径的环境建模

环境建模是把机器人运动空间用数学建模描述出来，它是路径规划必不可少的部分。目前环境建模的方法有栅格法、多边法、单元树法等。本文采用栅格法[18]将机器人和障碍物位置用栅格单元来描述，易于计算机存储和操作，算法简单直观且容易编程。栅格法是把机器人所处的运动空间转化为具有二值信息的网格单元，用相同尺寸的网格对二维运动空间进行划分。划分的栅格内含有障碍物的为障碍栅格，不含有障碍物的为自由栅格。

图1为用栅格法建立的机器人路径规划，黑色部分为障碍栅格，白色部分为自由栅格，左上角和右下角的栅格分别为起点和终点，用黑格白环表示。

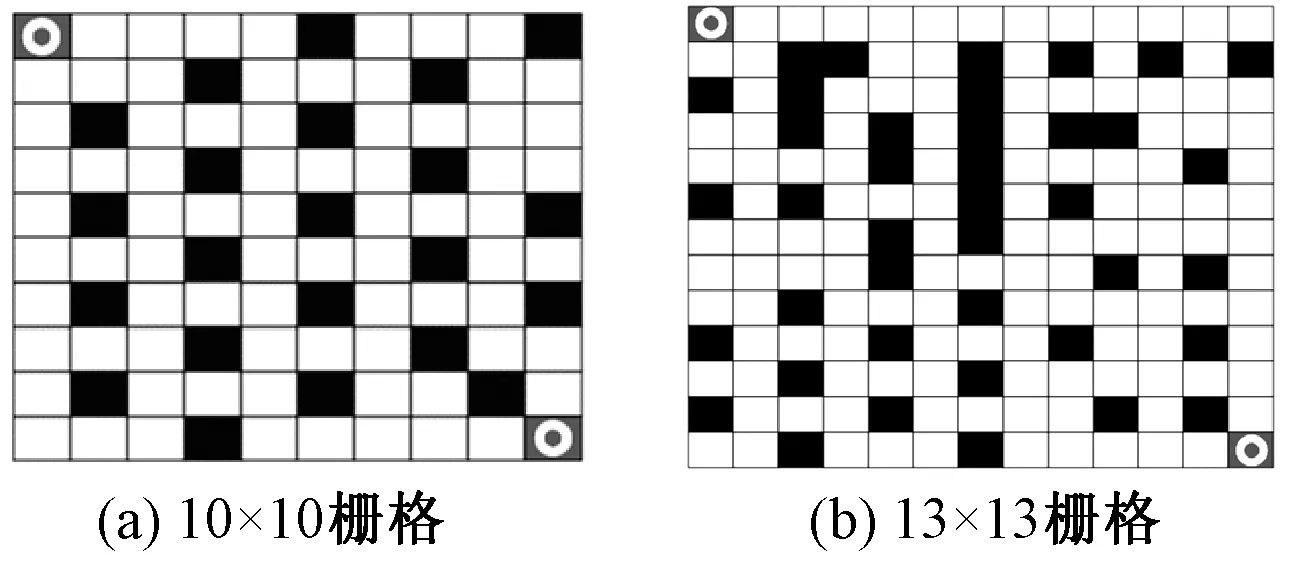
图1 栅格法建立的机器人路径规划Figure 1 Robot path planning by grid method

2.2 路径决策规则

1)建立初始决策表

机器人路径规划主要是躲避障碍物和找出最优路径，采用粗糙集约简推导出最小化决策表。在机器人工作环境的栅格模型中，假设机器人在栅格中所处的位置为Pi，下一步移动的方向有8个，机器人路径栅格方向如图2所示。

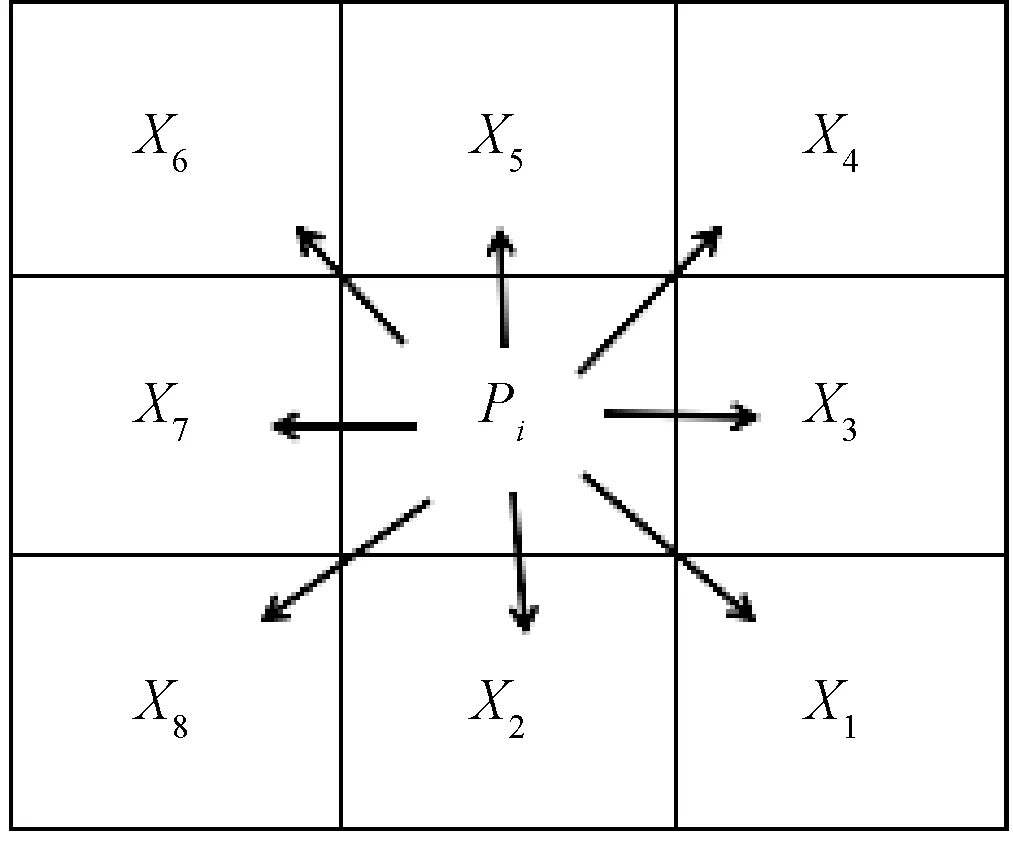
图2 机器人路径栅格方向Figure 2 The direction of robot path grid

设U为对象的论域，共有4 374条规则，将这8个方向作为条件属性，量化可得C={X1,X2,X3,X4,X5,X6,X7,X8}。条件属性值用1、2和3表示，其中1为障碍栅格，2为Pi-1的自由栅格，3为自由栅格。Y为决策属性，属性值表示下一步将要搜索栅格点的行为(共8类)，初始决策表如表1所示。

2)简化决策规则

表1是一张二维数据表，每一行描述的是一个对象(决策规则)，每一列描述的是该对象的一种属性。根据定义3和定义4对初始决策表中的属性进行约简，在保证不影响决策属性值的情况下，删除冗余条件属性列。经计算可得，属性X4、X6和X8是冗余属性并将其删除。对决策规则进行约简，得到如表2所示的简化决策表。

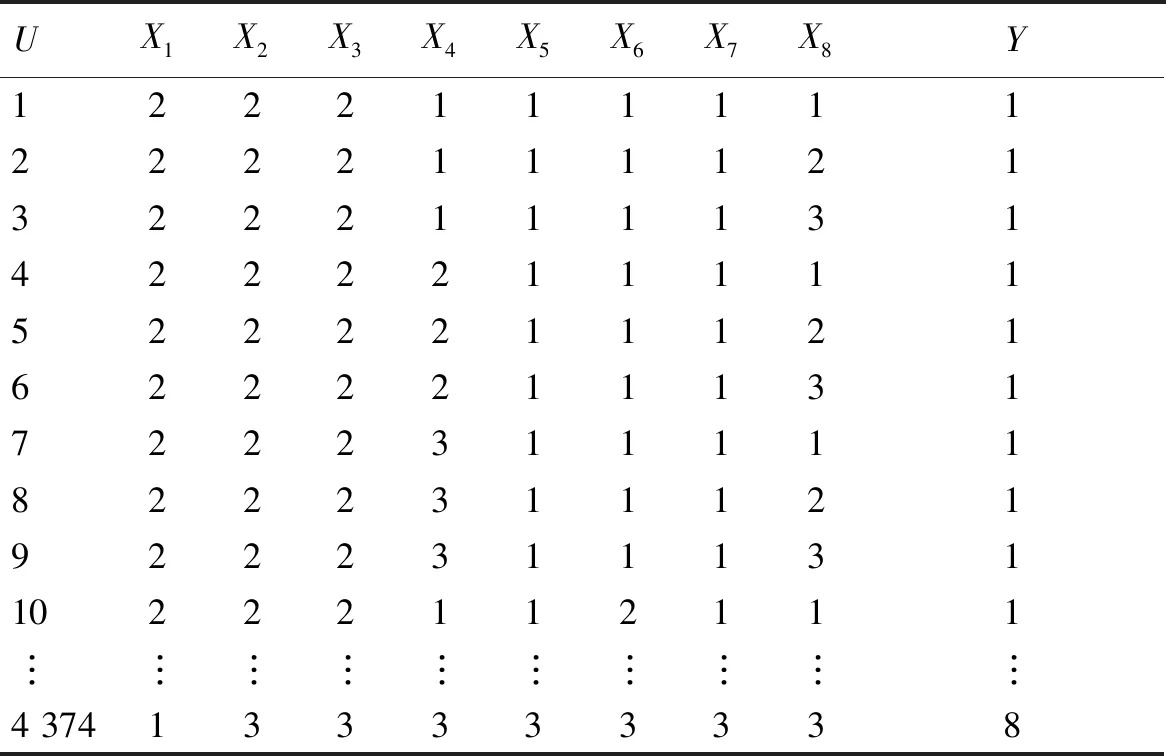
表1 初始决策表Table 1 Initial decision table

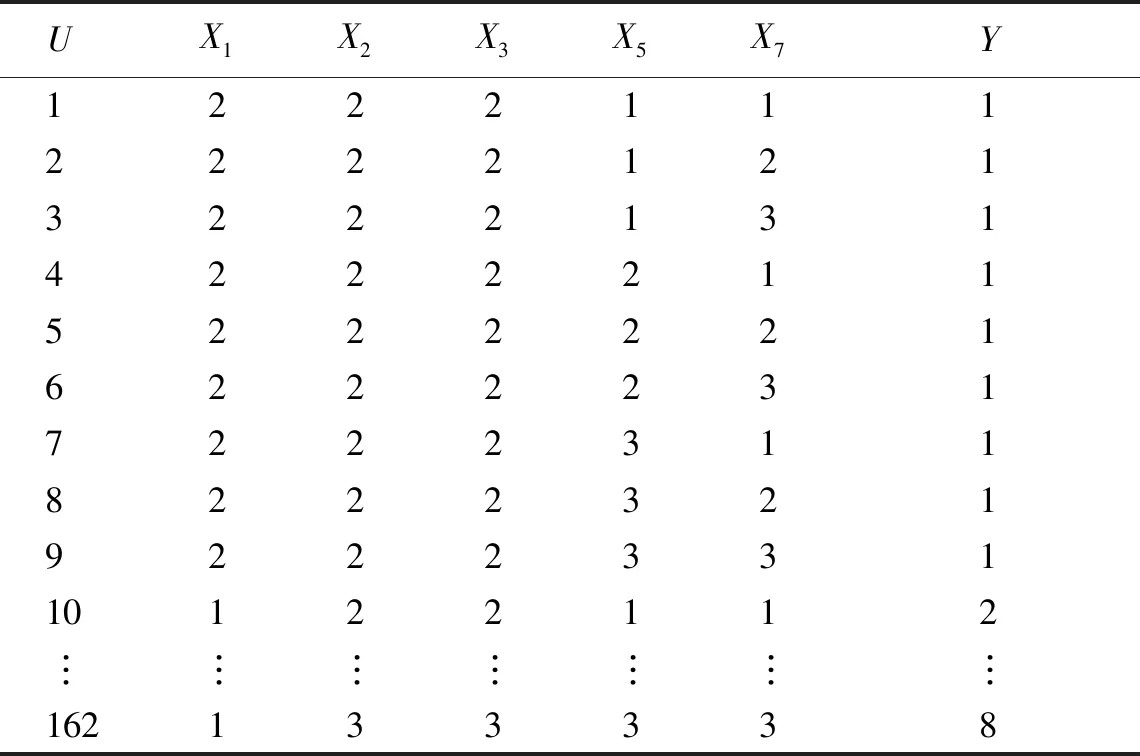
表2 简化决策表Table 2 Simplified decision table

3)最小化决策表

删除冗余属性后，剩下162条决策规则，再从这些规则中删除与相同决策类相关的冗余决策规则，得到如表3所示的最小化决策表，表中“-”表示任意属性值。从162条决策规则中去掉冗余信息和重复信息后，得到了80条最小决策规则。

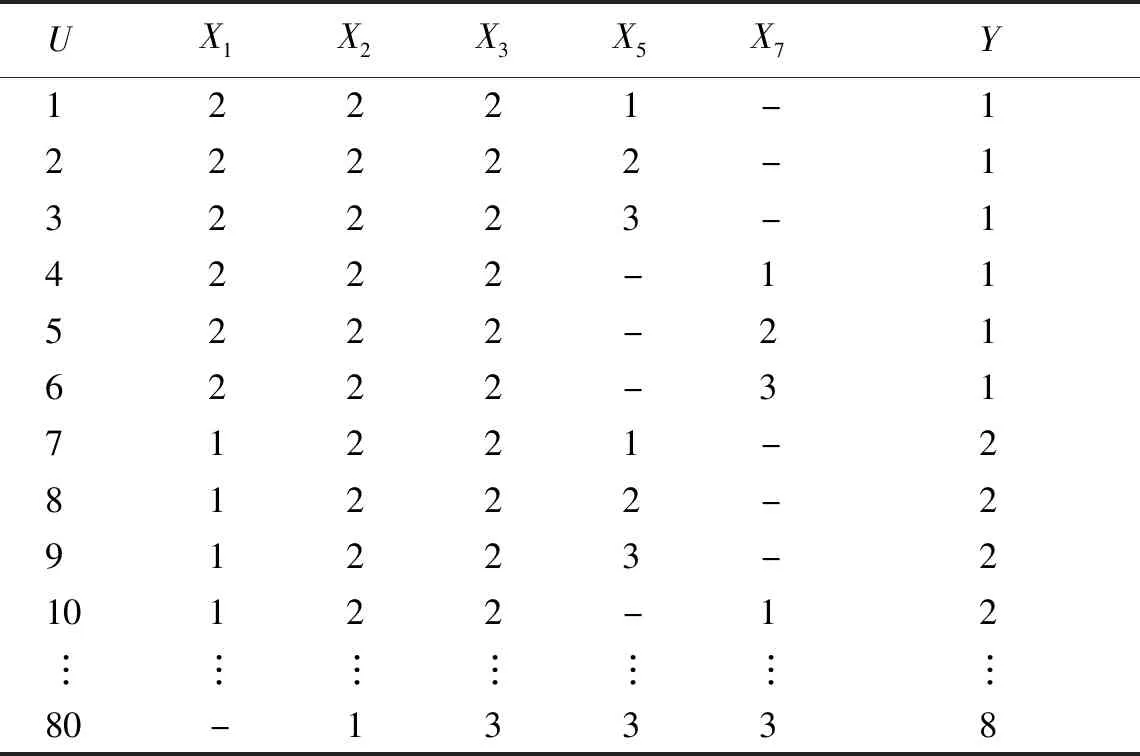
表3 最小化决策表Table 3 Minimized decision table

经过以上约简处理，从最初的8个条件属性中获得5个最简条件属性，从4 374条决策规则中提取80条最小决策规则，有效减小了机器人路径规划的规模，为提高机器人搜索速率提供了可能性。

2.3 机器人路径规划算法

在针对全局环境建立的二维栅格化环境模型中引入粗糙集软计算方法，简化狮群优化算法的初始种群，由粗糙集训练获得一系列可行路径。在序号编码基础上根据栅格之间的关系和障碍物分布情况，利用约简得到的最简条件属性和最小决策规则，训练产生一系列可行路径作为狮群算法的初始种群。具体步骤如下。

步骤1 根据栅格法建立机器人路径的工作环境，环境建模如2.1节所述；

步骤2 种群初始化，产生一些序号编码的初始种群；

步骤3 通过路径决策规则进行知识约简，再对知识约简后的初始种群进行训练，产生一系列可行路经，并计算狮子个体适应度值；

步骤4 根据适应度值和式(2)确定狮子种群的构成，最优的适应度值位置为狮王位置；

步骤5 根据式(3)更新狮王的位置，在式(4)和式(9)中加入惯性权重ω，更新雌狮和幼狮的位置；

步骤6 根据狮子的位置计算适应度值，对狮子的位置采用回溯法进行选择，并更新狮子个体的历史最优位置和狮子群体的历史最优位置；

步骤7 判断是否满足终止条件(全局最优路径或最大迭代次数)，若满足，输出机器人的最短路径，否则转至步骤4。

在步骤5中，为了平衡狮群中雌狮的局部寻优能力和幼狮的全局寻优能力，引入了惯性权重ω，其计算公式为

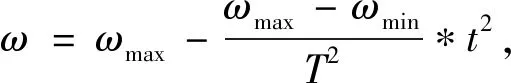
(10)

其中：ωmax为最大惯性权重，取0.99；ωmin为最小惯性权重，取0.35。

加入惯性权重ω后，式(4)转化为

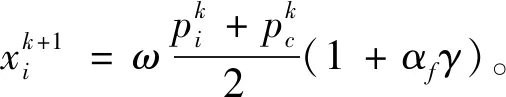
(11)

式(9)转化为

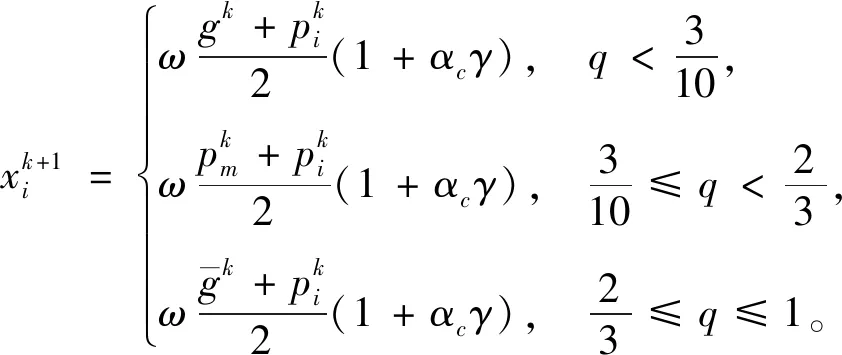
(12)

在狮群迭代初期，狮子需要较大范围的全局搜索，ω变化缓慢，有利于在迭代初期寻找最优解范围。在找到最优解范围后，进入算法后期，这时狮群需要以较慢速度局部搜索，ω变化加快，有利于在较短时间内收敛到最优值。

3 结果与分析

采用Matlab语言编程，实验环境为：Intel Core i7 2.8 GHz CPU；8 GB内存；1 000 GB硬盘；Windows 10操作系统。首先建立如图1所示的10*10和13*13栅格初始环境模型；其次采用粗糙集路径决策规则对初始种群进行训练，输出最小化决策表；最后根据改进的狮群算法寻找机器人最优路径。与本文算法(ILSO)进行对比的算法有遗传算法(GA)[11]、粒子群优化算法(PSO)[10]、狮群优化算法(LSO)[14]。根据文献[14]和[19]给出的参数设置原则，初始种群规模设为20，迭代次数为50。

采用适应度函数来评价机器人寻找最优路径的优劣，由于采用的是基于栅格法的环境建模，所以适应度函数可以表示为

f=d，

(13)

其中：d表示机器人通过栅格的总数。实验是在10*10栅格二维图和13*13栅格二维图中进行的。

3.1 10*10栅格中路径规划

GA、PSO、LSO、ILSO在10*10栅格中各自的路径规划如图3所示，输出的最优路径长度分别为17、17、13和12，ILSO的路径长度最短。在10*10栅格中，4种算法的适应度值变化趋势见图4。可以看出，当迭代次数为50时，LSO在收敛速度和适应度值上优于PSO和GA，而ILSO在迭代次数不到10时就收敛到最优值，比其他3种算法收敛速度快，适应度值也明显优于其他算法。表4列出了4种算法迭代50次的最小适应度值、平均适应度值和运行时间。可以看出，在这3个指标上ILSO是最优的，其次是LSO，PSO的最小适应度值等于GA，但GA的平均适应度值和运行时间低于PSO。

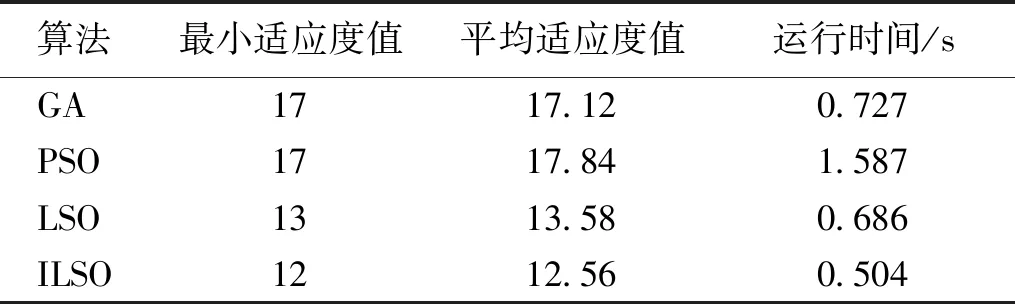
表4 10×10栅格中4种算法的适应度值和运行时间Table 4 Fitness values and running time of four algorithms in 10×10 grid

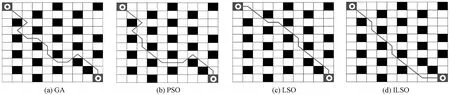
图3 10×10栅格中4种算法的路径规划Figure 3 Path planning of four algorithms in 10×10 grid

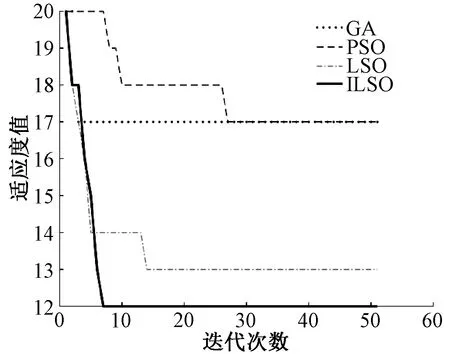
图4 10×10栅格中4种算法的适应度值变化趋势Figure 4 Trend of fitness values of four algorithms in 10×10 grid

3.2 13*13栅格中路径规划

GA、PSO、LSO、ILSO在13*13栅格中各自的路径规划如图5所示，输出的最优路径长度分别为31、23、17和16，ILSO的路径长度最短。在13*13栅格中，4种算法的适应度值变化趋势见图6。可以看出，ILSO在迭代次数不到10时就收敛到最优值，算法收敛速度最快，适应度值明显优于LSO、PSO和GA。表5列出了4种算法迭代50次的最小适应度值、平均适应度值和运行时间。可以看出，在这3个指标上ILSO仍然是最优的。

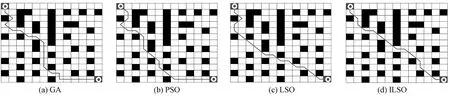
图5 13×13栅格中4种算法的路径规划Figure 5 Path planning of four algorithms in 13×13 grid

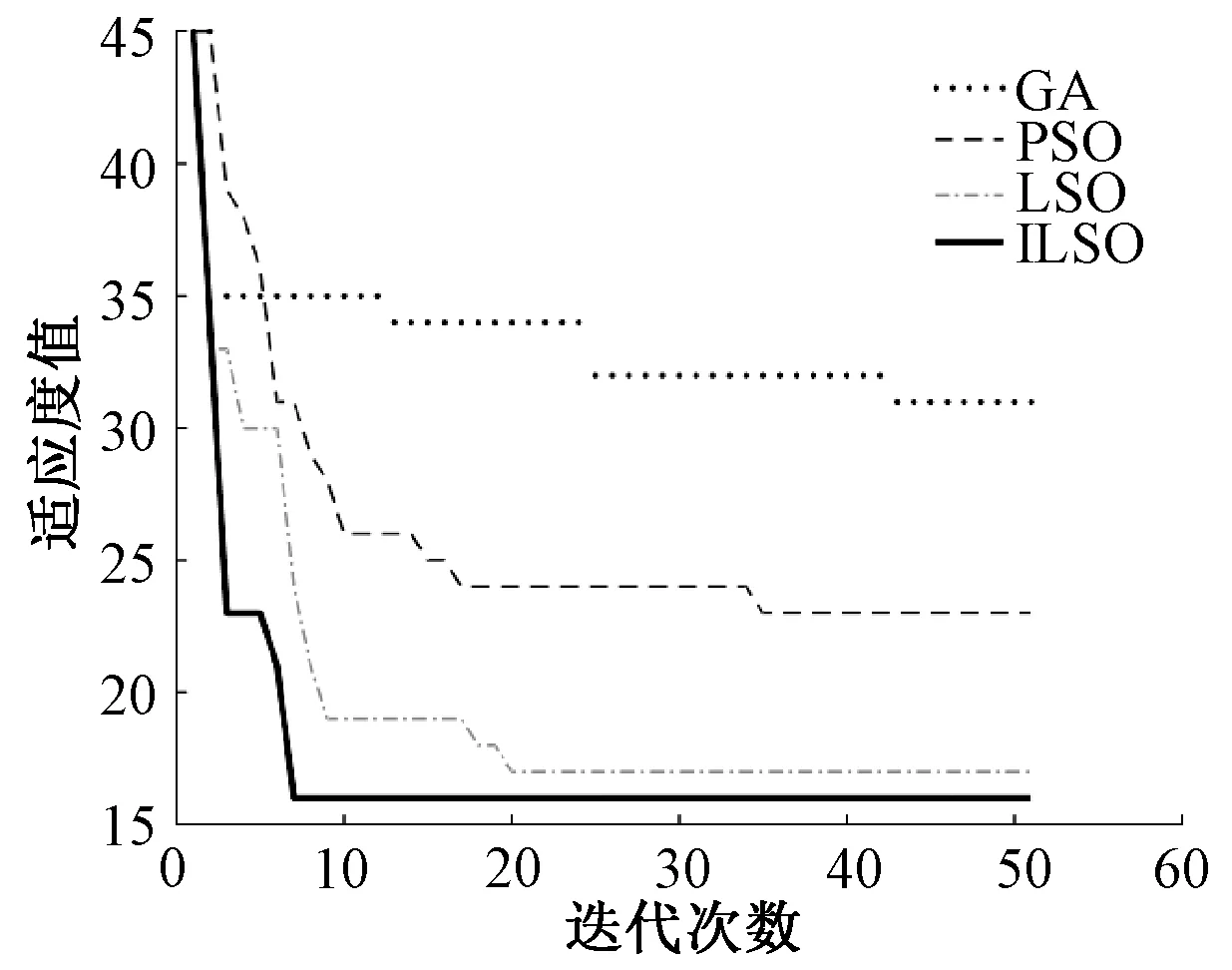
图6 13×13栅格中4种算法的适应度值变化趋势Figure 6 Trend of fitness values of four algorithms in 13×13 grid

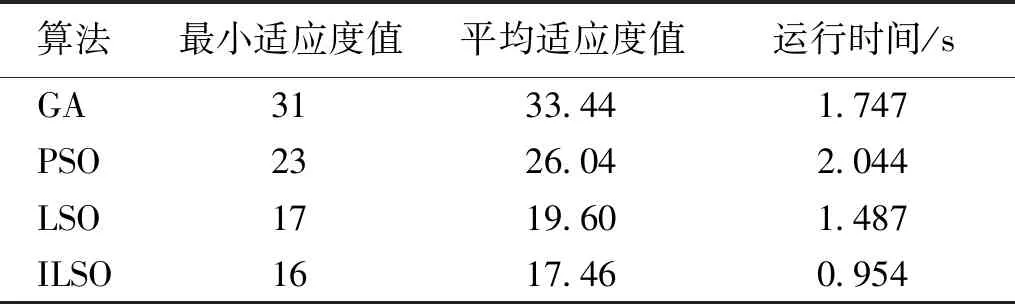
表5 13×13栅格中4种算法的适应度值和运行时间Table 5 Fitness values and running time of four algorithms in 13×13 grid

13*13栅格与10*10栅格相比，随着栅格数量和障碍数量的增加，4种算法各自的最小适应度值与平均适应度值均有所增加。在13*13栅格中，ILSO的最小适应度值与平均适应度值的差值在1.5以内，而其他算法的最小适应度值与平均适应度值的差值在2.4以上，进一步表明ILSO具有相对更好的稳定性。综上，相较于GA、PSO、LSO，本文算法在机器人路径规划问题中具有收敛速度快、寻优能力强和稳定性好的优势。