Schrödinger-Poisson系统解的存在性
2022-02-24钟巧澄
王 军,王 莉,钟巧澄
(华东交通大学 理学院,江西 南昌 330013)
0 引言
本文考虑下列Schrödinger-Poisson系统:
(1)
其中:位势函数V是不定的,即V有有限维负空间;Ω是R3的有界子集。
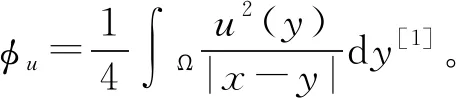

文献[2-11]研究了Schrödinger-Poisson系统各种解的存在性,但在不定位势的情形下的研究较少。对于不定位势的问题,正如文献[12]所述,由于V在某些地方可能为负,能量泛函I将不再满足一般的环绕定理。文献[13]利用Morse理论得到方程(1)非平凡解的存在性。本文在其基础上考虑更一般的增长性条件,并在此条件下依然得到相同的结果。本文还运用改进后的Clark’s定理得到无穷多解的存在性。对位势函数V作如下假设:



对于非线性项,作如下假设:
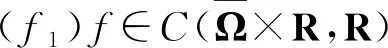
为了保证全局紧性,通常对非线性项f(x,t)施加次临界增长性条件:存在一个常数C0>0使得:

其中:1 αG(x,t)+c≥G(x,st) 成立,其中G(x,t):=tf(x,t)-4F(x,t)≥0。 αG(x,t)≥G(x,st) 成立,这等价于(f2)当c=0。 显然,F(x,t)=t4ln(1+t4)满足条件(f1)~(f3)。 下面陈述本文的主要结果: 定理1 假设条件(V)和条件(f1)~(f3)成立,那么方程(1)有一个非平凡解。 定理2 假设条件(V)和条件(f1)~(f3)成立,如果f(x,·)是奇函数,那么方程(1)有一列解使得I(un,φn)→+∞。 定理3 假设条件(V)和条件(f1)~(f3)成立,如果f(x,-t)=-f(x,t)对所有(x,t)∈Ω×R都成立,那么方程(1)有一列解{uk}满足当k→∞时有‖uk‖X→0。 下面回顾无穷维Morse理论的一些概念和结论。 设X是一个Banach空间,I:X→R是一个C1的能量泛函,u是I的一个孤立临界点以及I(u)=c,那么: Cq(I,u):=Hq(Ic,Ic{0}),q=0,1,2,… 称为I在u的第q阶临界群,其中Ic:=I-1(-∞,c]和H*表示系数在z上的奇异同调。 若I满足Palais-Smale(PS)条件(即任意满足I(un)→c,I′(un)→0的序列{un}有收敛子列)且I的临界值有下界α,那么由文献[14]可知: Cq(I,∞):=Hq(X,Iα),q=0,1,2,… 指I在无穷远处的第q阶临界群。众所周知,上式的右边并不取决于α的选择。 命题1[15]如果I∈C1(X,R)满足PS条件且对于某些k∈有Ck(I,0)≠Ck(I,∞),那么I有一个非零临界点。 命题2[16]假设I∈C1(X,R)在0处局部环绕,即X=Y⊕Z且对于某些ρ>0有: I(u)≤0,∀u∈Y∩Bρ; I(u)>0,∀u∈(Z{0})∩Bρ, 其中:Bρ={u∈X|‖u‖≤ρ}。如果k=dimY<∞,那么Ck(I,0)≠0。 为了研究泛函I,本文将利用涉及φu的项的以下性质: 命题4[18]设X是一个Banach空间,I∈C1(X,R)。假设I满足PS条件,是偶泛函和下有界的,以及I(0)=0。如果对于任意的k∈,存在X的一个k维子空间Xk和ρk>0使得其中那么下列结论至少有一个成立: X上的等价范数,泛函I可以改写为: (2) 其中:u±表示u在X上的正交投影。 引理1 若条件(V)和条件(f1)~(f3)成立,那么泛函I满足PS条件。 证明对于c∈R,设{un}是X上的PS序列,即I(un)→c且I′(un)→0,n→∞,这表明: c=I(un)+o(1)且〈I′(un),un〉=o(1)。 (3) 在X上,wn弱收敛到w, 在Lr(Ω)(2≤r<2*)上,wn强收敛到w, 在Ω上,wn几乎处处收敛到w, (4) 设Ω1={x∈Ω,w(x)≠0},则在Ω1上有: 因此, |un(x)|→+∞几乎处处在Ω1上。 (5) (6) 再次利用条件(f3),存在常数C2>0使得对任意x∈Ω和|t|≤C2,有: (7) F(x,t)≤M。 (8) (9) 接下来证明|Ω1|=0。如果|Ω1|≠0,那么结合命题3、式(4)、式(6)、式(9)和Fatou引理,可得: (10) I(tnun)→+∞当n→∞。 (11) 由于I(0)=0,I(un)→c,所以tn∈(0,1)且 (12) 根据假设条件(f2),对于0≤tn≤1有αG(x,un)+c≥G(x,tnun),那么利用式(11)和式(12)可得: (13) (14) 证明反证。存在序列{un}⊂X使得I(u)≤-n但 (15) 因此, 4I(un)-〈I′(un),un〉≤-4n。 (16) 因此,利用式(15)可得: 这与式(16)矛盾。引理2证毕。 引理3Cq(I,∞)=0,q=0,1,2…。 成立。所以存在sv>0使得I(svv)=-A。令u=svv,则根据引理2可得: 因此,Cq(I,∞)=Hq(X,I-A)=Hq(X,XB)=0,q=0,1,2,…。引理3证毕。 定理2的证明 根据引理1可知I满足PS条件,定理2的证明与文献[12]中定理1.2的证明非常类似,故这里不再重复。 定理3的证明 根据f(x,-t)=-f(x,t),易证泛函I是偶泛函以及满足I(0)=0。此外,由于V∈C(Ω)有界,显然I是下有界的。对于∀k∈和ρk>0,令
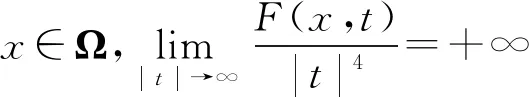
1 准备工作
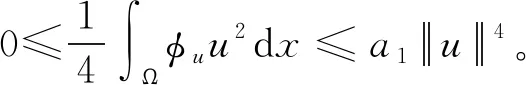

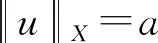
2 重要引理

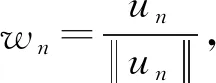


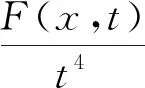

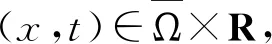
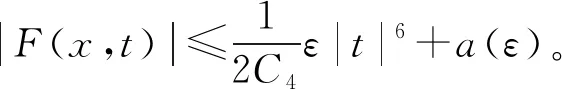
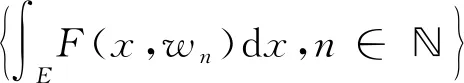

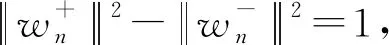


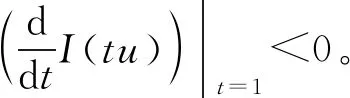
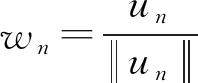

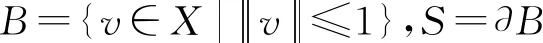
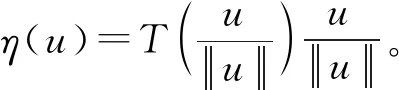
3 定理的证明

