基于新型滑模参数观测器的异步电动机MPC策略

孙军涛，殷智祺，陆新东，侯永辉，袁震，陈鑫

（1.河南省计量科学研究院，河南 郑州 450000；2.南阳防爆电气研究所有限公司，河南 南阳 473000）

模型预测控制（model predictive control，MPC）理论起源于20世纪80年代，后凭借其多目标、易添加约束条件和动态特性好等特点，在异步电动机控制领域取得了广泛的应用[1-3]。根据控制目标不同，异步电动机MPC方法主要被分为模型预测控制[4]、模型预测转矩控制[5]和模型预测转速控制[6]三大类，它们的实现方法是利用MPC控制器代替传统矢量控制或直接转矩控制方案中的PI控制器，以克服传统方法中参数校核复杂和动态响应速度慢的缺点。

与传统PI控制器不同，MPC控制器利用状态反馈信息以及离散系统模型预测未来状态，并根据评价函数选择并施加最优电压矢量。因此，异步电动机MPC是一种基于系统模型的控制方法，系统参数的准确度对MPC控制性能有显著影响[7]。一般地，用于预测计算的异步电动机定子参数（电阻和电感）是由生产厂家通过离线测试得到的。但由于异步电动机结构特点，与转子相关的参数（如转子电感以及定转子间互感等）无法利用测试仪器直接测量获得，工程中一般采用信号注入法实现参数辨识。文献[8]直流信号注入，在空载-堵转条件下运用最小二乘法，测得电机的定转子漏感和励磁电感等电机参数；考虑到堵转在实际中不容易操作，文献[9-10]通过向电机输入单相交流或直流阶跃电流，并检测其响应，从而计算求得电机的参数。可以看出，信号注入法本质上仍属于离线检测方法，只能在特定的环境与工作状态下完成。考虑到转子电阻及电感在实际中会随着工作温度、饱和情况而不断变化，导致实际值与检测值之间存在误差，但是当把不准确的转子参数用于MPC估计未来状态并选择最佳控制量时，会产生稳态控制误差，严重时影响系统的稳定性[11]。为解决参数失配问题，文献[12-15]采用实时在线参数辨识法获取系统参数，观测到的实时参数可被用于预测计算过程中，保证良好的控制性能。文献[12]采用全阶自适应观测器辨识异步电动机转子电阻和电感等参数；文献[13]建立了电机模型并采用扩展卡尔曼滤波器实现对转子参数的在线估计；文献[14]设计了一个双复合滑模面滑模观测器在线辨识异步电动机转子电阻，用于提高异步电动机间接磁场定向矢量控制性能；文献[15]利用最小二乘法实现了异步电动机转子电感和电阻实时观测。在线参数检测法无疑为解决MPC控制受参数不匹配影响而性能下降的问题提供了思路，在工程应用中具有重要的价值。

由文献[14]可知，由于变结构滑模观测器具有强鲁棒性和易执行的优势，已经在异步电动机转子参数辨识中取得了应用。然而，传统的基于开关函数趋近律的滑模观测器在应用中会有明显的抖振现象，需要采用低通滤波器抑制抖振带来的影响，但低通滤波器的延时效果会降低所观测参数的实时性，进而对MPC的预测精度产生影响。

本文提出了一种用于在线辨识异步电动机转子自感及定转子互感参数的滑模观测器，并将实时估算参数用于MPC预测过程中，以提高系统的控制精度。为解决传统滑模观测器抖振问题，采用一种新型的基于双曲正切函数趋近律的滑模观测器，优势为：不再使用低通滤波器，可避免由此引入的延时，所观测的参数具有更强的实时性。

1 异步电动机模型

构建滑模转子参数观测器和MPC控制器需要依靠异步电动机模型，考虑到转子磁场定向技术能够实现自然解耦，本文建立异步电动机在M-T轴旋转坐标系下的模型[16]如下：

式中：isM，T为定子M，T轴电流；irM，T为转子M，T轴电流；usM，T为M，T轴控制电压；Lm为定转子互感；Ls为定子自感；Lr为转子自感；Rs，Rr分别为定、转子电阻；ωr，ωe和Δω分别为电机实际转速、同步转速与转差速率；J为转动惯量；Te，TL分别为电磁转矩与负载转矩；p为电机极对数；B为阻尼系数；Ψr为转子磁链，可由转子磁链观测器估算得到[16]。

式（1）～式（3）分别为电机定子电气模型、转子电气模型和机械模型。由于模型预测电流控制只需要对定子模型进行离散化处理，且模型中的转子电流无法直接测量，异步电动机电气模型需要进一步简化。

首先，将转子模型代入式（1）可得：

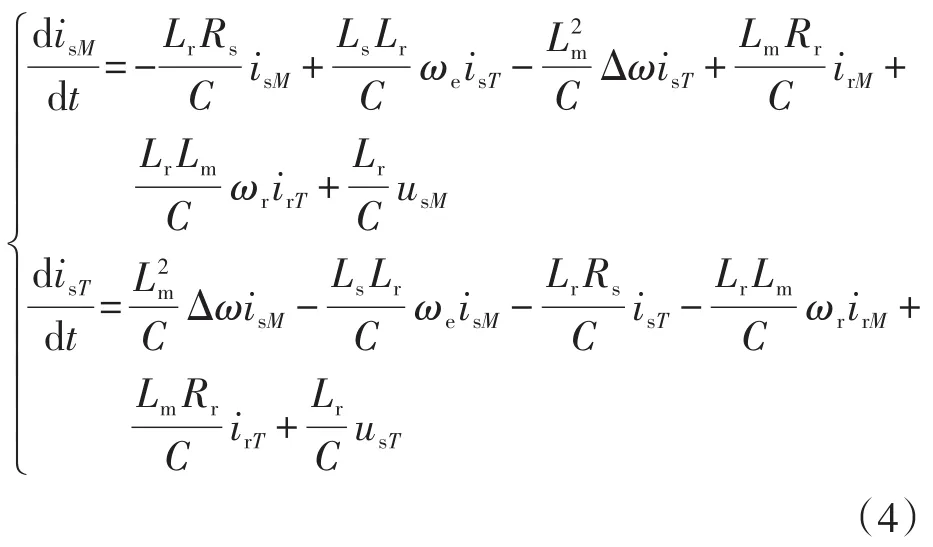
式中：C为电感常数。

其次，考虑到电机模型是根据转子磁链定向理论建立，转子M，T轴磁链ΨrM和ΨrT满足以下条件[17]：

式中：T1为转子绕组电气时间常数。

由式（5）可得，转子磁链与定子电流之间为一阶延时关系，即当定子电流改变时，转子磁链会有相同的变化趋势。考虑到转子绕组电气时间常数非常小，延时效应可以忽略，可以得到：

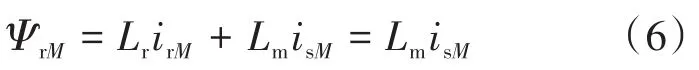
即在M-T坐标系下，转子M轴电流可近似地满足以下条件：

将式（5）～式（7）代入式（4），异步电动机模型可表示为

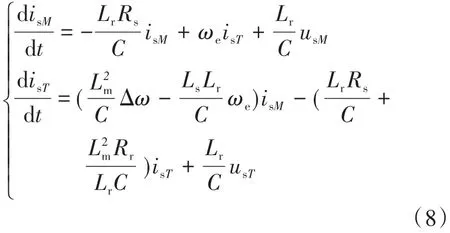
由于式（8）中不包含不可检测的转子电流信息，适合于直接构建MPC控制器及滑模转子参数观测器。

2 新型滑模转子参数观测器

对于异步电动机而言，与转子相关的电感参数包括转子自感与定转子互感，本节以电机模型为基础，构造以双曲正切函数为趋近律的变结构滑模观测器，实现电感参数在线辨识。

2.1 双曲正切函数趋近律

根据文献[18]，可通过设计连续型趋近律来削弱滑模观测器抖振现象，常用的连续型开关函数包括饱和函数和s-函数，这些函数具有以下特点：1）当变量值趋于-∞和+∞时，函数值趋于-1和1；2）开关函数为奇函数；3）在0处连续可导。然而，对于满足这些条件的双曲正切函数，将其用于构建滑模观测器的研究非常少。双曲正切函数的表达式为

其中，a为常数，用于调节函数曲线在0附近的斜率，使得趋近律接近实际系统的真实特性，从而降低抖振带来的影响。

2.2 新型滑模观测器设计

由式（3）和式（8）可以看出，Lm和Lr没有以独立系数的形式出现在表达式的某一项中，这导致无法利用滑模观测器直接辨识转子电感与定转子互感。为解决该问题，本文先构建滑模观测器估算Lr/C和Lm/Lr的值，然后通过解析计算得到电感值。根据M轴电流方程和机械方程，Lr/C和Lm/Lr观测器构建为

其中

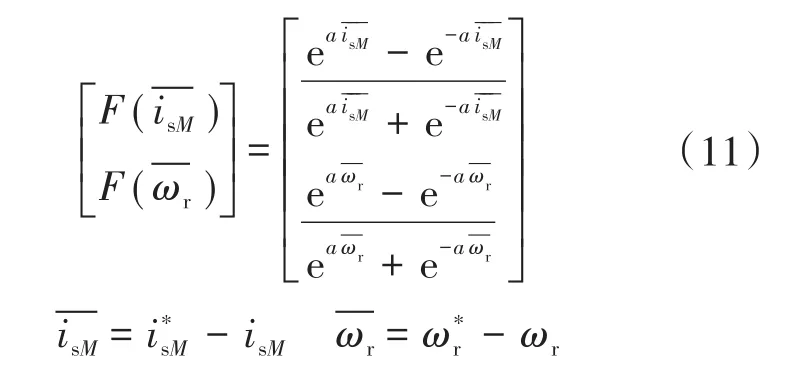
在实际应用中，当滑模观测器稳定后，由式（11）辨识得到的Lr/C和Lm/Lr满足以下条件：

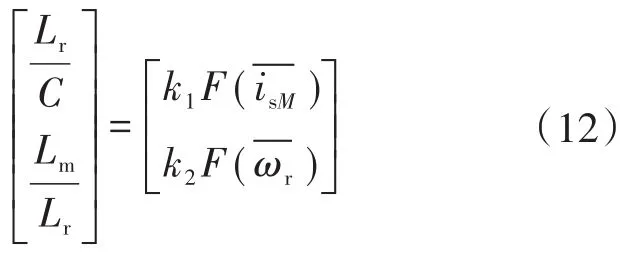
进而，Lr和Lm满足以下方程组：

解方程组可得估算转子自感与定转子互感为

所提出的新型滑模转子参数观测器实现框图如图1所示。在应用中，将检测得到的转速和T轴电流输入观测器，并根据所施加的电压和负载转矩计算出Lr/C和Lm/Lr的值，然后利用式（14）便可估算出实时电感值Lm和Lr。

图1 新型滑模转子参数观测器实现框图Fig.1 Implementation diagram of the proposed novel sliding mode rotor parameter observer

2.3 稳定性分析

与传统的基于符号函数趋近律的滑模观测器一样，Lyapunov方程是分析新型滑模观测器稳定性的重要手段。首先，定义滑模面SS为

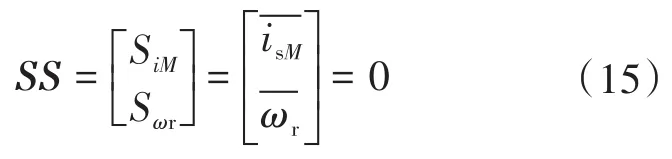
构造Lyapunov方程为

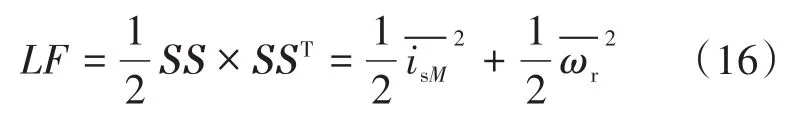
对Lyapunov方程求导得：

另外，根据式（3）、式（8）和式（10）可得：

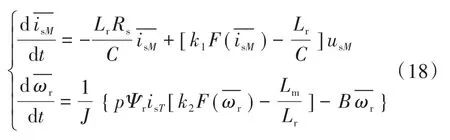
将式（18）代入（17）可得：

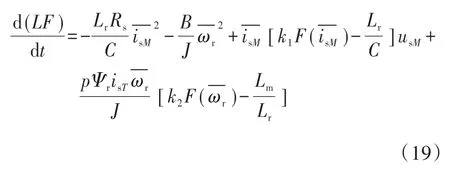
其中，第1项和第2项为负值，为保证滑模观测器稳定，需要令第3项和第4项满足小于0的条件，即

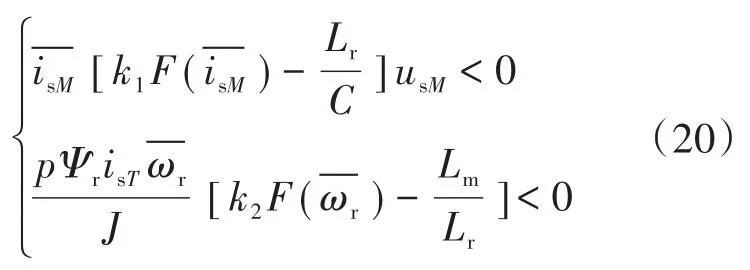
由于实际控制，usM为负值，而isT为转矩电流，考虑阻尼影响，其为正值，且p，Ψr和J是正值[16]，则式（20）可进一步化简为下两式：

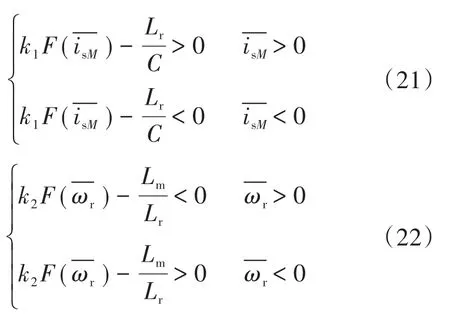
进而可得滑模观测器稳定性条件为

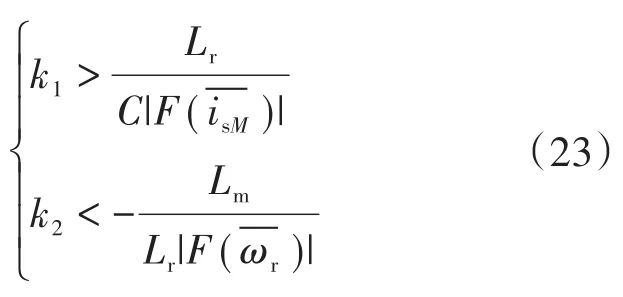
由于双曲正切函数值范围为（-1，1），要保证系统绝对稳定，理论上k1和k2应取无穷大，但这在工程应用中是无法实现的。考虑到表示估算值与实际值之间的误差，可接受的误差范围是可人为设置的，且只要该误差足够小，系统也可认为是稳定的，记最小电流和转速估算误差分别为ξi和ξωr，即

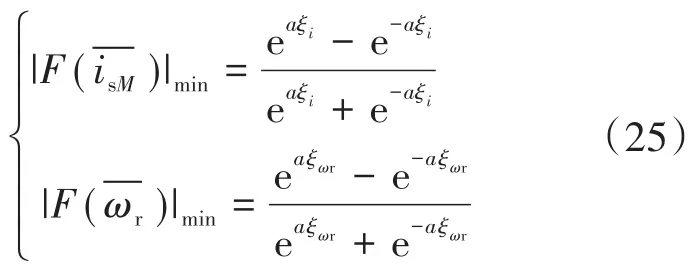
故当k1和k2满足以下条件时，电流和转速真实值与估算值间存在很小的误差，滑模观测器将维持稳定。

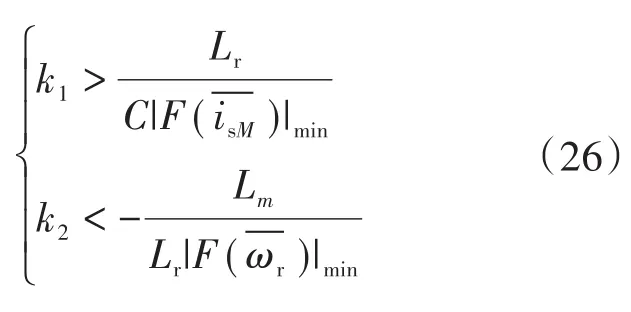
3 基于转子参数观测器的MPC

利用Euler法将异步电动机定子电流模型离散化得到用于MPC的预测模型如下：

式中：isM（k），isT（k），ωe（k）和Δω(k)为当前时刻状态量；isM（k+1），isT（k+1）为1个采样周期Ts后的预测电流值；usM（k），usT（k）为控制电压。

有限集MPC在每一控制周期内可选择的电压矢量是固定的，对于两电平逆变器而言，共有7个可用电压矢量（6个有效电压矢量和1个零电压矢量），即S0=[0，0，0]T，S1=[1，0，0]T，S2=[1，1，0]T，S3=[0，1，0]T，S4=[0，1，1]T，S5=[0，0，1]T和S6=[1，0，1]T，对应的三相电压为

利用a-b-c/M-T坐标变换得到用于预测计算的M，T轴7个电压矢量为

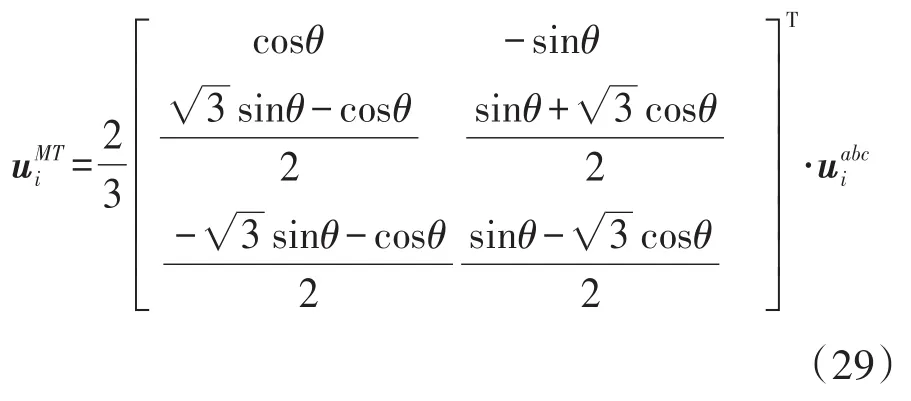
式中：θ为磁链角度。

在1个采样周期内，根据当前电动机转速、位置和电流信息，将7个待选电压矢量分别代入预测模型得到预测电流isM（k+1）和isT（k+1），值得注意的是，式（27）中的转子自感和定转子互感参数采用滑模转子参数观测器的估算值；然后，计算出对应的代价函数值，并通过比较选择，使代价函数最小的电压矢量及开关状态发送该周期的控制信号，便可实现基于滑模观测器的MPC。其中，以电流为控制目标的代价函数为

4 实验验证及结论

为验证所提转子参数观测方法及有限集MPC控制方法的有效性，搭建一套异步电动机测试平台进行算法验证，平台参数如下：转速500 r/min，直流电压Udc=310 V，转矩TL=5.5 N·m，定子绕组电感Ls=0.17 H，定子电阻Rs=0.55 Ω，转子电阻Rr=0.044 Ω，转动惯量J=0.000 5 kg·m2，摩擦系数B=0.000 1，控制频率10 kHz，由厂家提供的转子自感和定转子互感分别为95 mH和75 mH。试验控制平台以DSP TMS320F2812为主控芯片，逆变器采用智能功率模块（IPM）PM20RLA（安全电流20 A），加载和记录转速由Magtrol公司的10 kW测功台完成。为了综合验证所提方法，实验设置如下：首先，利用离线测得的转子自感和定转子互感实现模型预测控制，同时执行滑模观测器算法辨识电感参数；其次，将由滑模观测器实时估算的电感值接入MPC控制器中，比较基于离线参数和在线参数MPC的性能差异；最后，电机由空载启动（参考转速为500 r/min），运行至5.0 s突加5.5 N·m恒定负载，在10.0 s时结束测试。

图2为基于离线参数的MPC控制性能。首先，MPC控制算法具有良好的稳态性能。异步电动机能够无误差跟踪转速参考值，当电机转速达到500 r/min后，转速波动值非常小，约为±30 r/min；另外，空载条件下，电机输出电磁转矩约为0.5 N·m，这是电机阻尼导致的，同时，T轴电流平均值约为1.2 A，说明式（20）中认为isT为正是合理的；isM在稳态条件下维持在0 A，波动大小约为±3 A。此外，电机也具有良好的动态性能，启动阶段电机转速无超调，上升时间约为0.6 s，转矩在加速阶段峰值达到6.8 N·m；M，T轴电流受限幅影响，最大值为20 A；在突加负载时，MPC控制算法体现出了良好的抗负载干扰鲁棒性，在短暂（1 s）调节后，系统恢复至稳定状态。为了更直观地对比电感参数对控制性能的影响，图2b给出了负载稳态条件下的相电流曲线。

图2 基于离线参数的MPC控制性能Fig.2 MPC control performance based on offline parameters

图3为由滑模转子参数观测器辨识得到的转子自感与定转子互感值。首先，转子自感与定转子互感并不是恒定值，这说明构建在线参数观测器是有意义的，在线参数辨识算法对实现高精度MPC控制算法具有很高的价值；其次，在稳态时，转子电感估测值在95 mH附近波动，相比于空载状态，带载条件下波动更大，互感值在75 mH左右波动，但波动幅度在空载和带载条件下相似。这表明本文构建的滑模转子自感和定转子互感观测器是有效的。

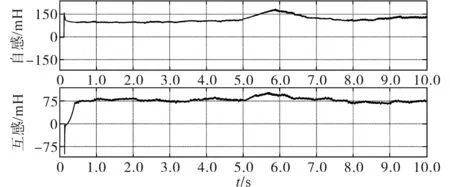
图3 转子自感与定转子互感估算值Fig.3 Estimation of rotor self-inductance and mutual inductance

图4为基于滑模转子参数观测器的MPC控制性能。与图1相似，异步电动机具有良好的稳态和动态性能，且转速、转矩和M，T轴电流与基于离线参数的MPC差距很小。然而，图4b给出相电流THD已经减小至6.54%，这说明采用实时估算参数后，系统的电流波动降低，稳态性能更好，进一步证明所提出的参数观测器对提高MPC控制性能具有重要意义。

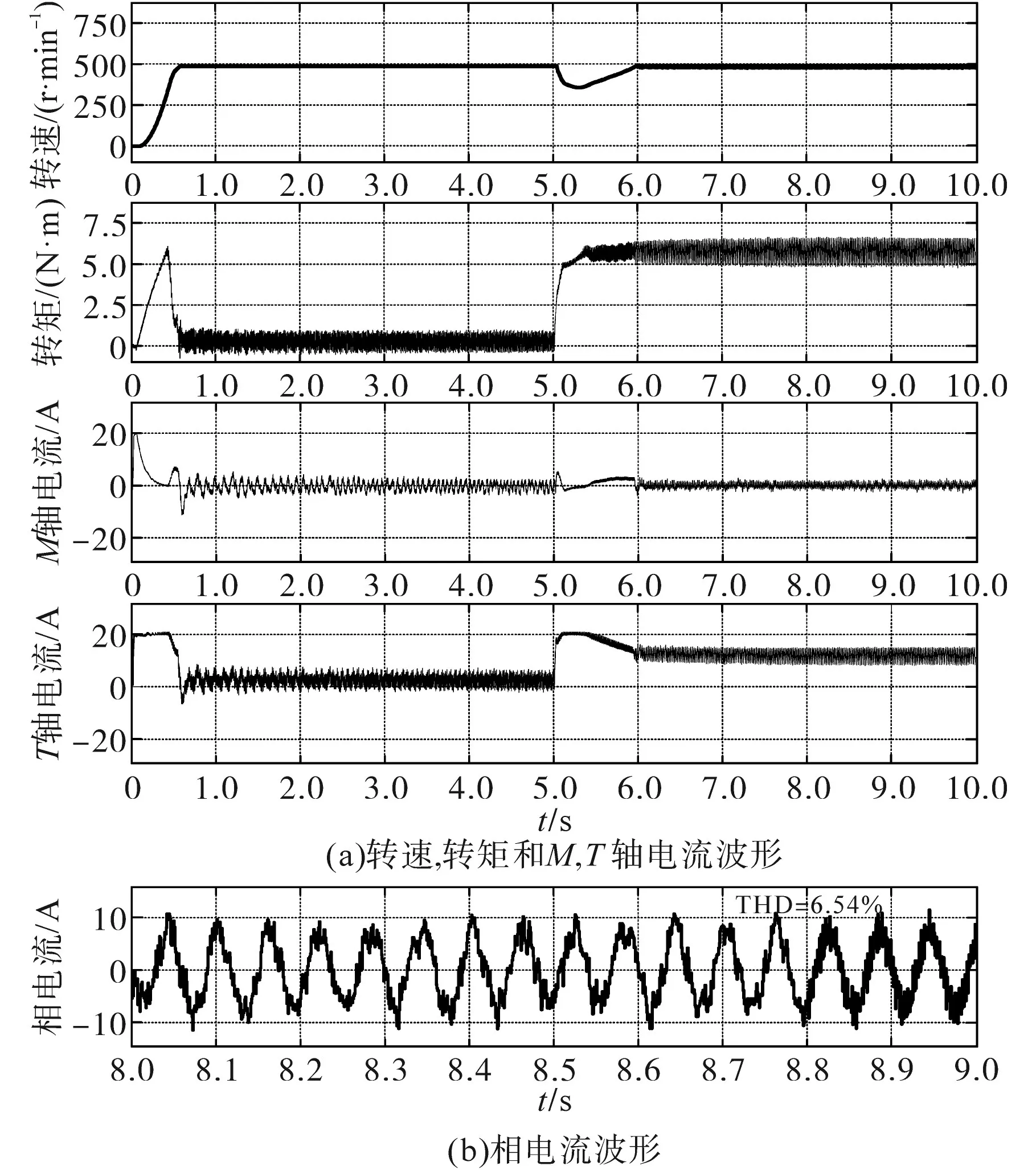
图4 基于滑模转子参数观测器的MPC控制性能Fig.4 MPC control performance based on sliding mode rotor parameter observer

为提高异步电动机控制性能，本文提出基于新型趋近律滑模转子参数观测器的MPC方法。首先，在搭建异步电动机模型后，依靠M轴电气方程和机械方程构建了基于双曲正切函数趋近律的滑模转子自感和定转子互感观测器，并通过构建Lyapunov方程对滑模观测器稳定性条件进行了分析。其次，利用异步电动机M，T轴电气方程实现了有限集模型预测电流控制方法，并将滑模观测器估算电感值融入进了MPC控制器中。最后，通过实验验证可得，所提出的基于滑模转子参数观测器的MPC比传统的基于离线参数的MPC具有更好的稳态性能，证明所提出的MPC具有较高的应用价值。