基于宽带相位修正的散射矩阵变极化基测量

白 杨, 侯 鑫, 刘 芳, 殷红成

(1. 北京环境特性研究所电磁散射重点实验室, 北京 100854; 2. 中国传媒大学信息工程学院, 北京 100024)

0 引 言

雷达目标极化散射特性通常用极化散射矩阵(polarization scattering matrix,PSM)表征。一般来说,散射矩阵具有复数形式,它随工作频率与目标姿态而变化,对于给定的频率和目标姿态特定取向,散射矩阵表征目标散射特性的全部信息[1]。在复杂目标极化特性研究中,通过测量手段获取其散射矩阵是最为常用的一种方法。依靠极化散射测试系统天线的极化组合形式,配合一定的极化定标算法,可以获得目标在某种特定极化正交基分解下的散射矩阵,若采用坐标系变换处理,则可以严格推导其他极化正交基分解或天线极化形式下的目标散射矩阵。正是由于散射矩阵测量获取的上述技术特点,大多数目标特性测量实验室只需要配备一种极化形式的测试天线(通常为线极化),而在需要获得其他极化基下的散射矩阵时,通过已有极化基的变换即可获得。

在进行散射矩阵变极化基测量时,要求初始极化基下获得散射矩阵各元素间的相位关系保持高度的相关性,否则会造成变换结果出现较大误差,影响这种相关性的因素主要有变换算法、标定方法和系统通道一致性三个方面。对于极化变换方法,文献[2-6]从不同的原始公式和表征方法出发进行了讨论,可在获取准确性PSM前提下方便地进行极化基变换,进而支撑目标识别等雷达极化学领域的应用,但并未关注实验测量中系统相位误差的传递问题,因此无法直接用于指导变极化基测量。对于极化幅相标定方法,文献[7-8]研究了三定标体校准方法,通过构造定标体复雷达散射截面(radar cross section,RCS)因子相消运算关系,即可避免对多个标准体进行位置测定的问题;而通过单定标体法进行极化校准,则避免了定标体位置摆放引起的相位测定误差[9]。而前述标定方法主要针对定标体特性展开校准算法,并未考虑测量系统极化通道相位不一致带来的测量误差,以及其对变极化基运算产生的影响。

本文主要针对多通道极化测量系统,研究在基于定标体散射完成散射矩阵幅相标定后,残留系统高频相移量引起的变极化基测量误差,进一步给出了一种基于一维宽带高分辨的相位修正方法,并通过标准体的实测数据,分析了修正前后变极化基测量结果的差别,验证了方法的有效性。

1 散射矩阵表征与极化基变换

对于平面波照射条件下,任何一对彼此正交且具有单位功率密度的极化波都可以作为目标PSM的极化基。在实验测量中常用的极化基是线极化基,对应于测试系统坐标系(或雷达坐标系)通常被表述为水平极化(H)和垂直极化(V),对应于被测目标边界面则可表述为平行极化(∥)和正交极化(⊥)。在某些特殊情况下需要获得目标在特殊极化基下的PSM,如圆极化(L极化、R极化),则可通过极化基变换由线极化PSM获得。

1.1 极化基变换

(1)

(2)

将式(1)展开可得

(3)

将式(3)代入式(2),整理可得

(4)

式(4)说明U是一个2阶酉矩阵[6-10],且有U-1=UH,|det(U)|=1。同时,由于复矩阵U定义了2组标准正交基间的变换,故其属于Householder镜像变换。

1.2 电磁波散射状态的变极化表征

(5)

在平面电磁波极化基变换时,涉及到两类情况:一是绕波矢量k旋转原有极化基,需采用旋转矩阵(实矩阵)表示;二是改变极化基各分量间的固有相位差。因此,不妨假设存在一个变换矩阵满足如下形式:

(6)

(7)

(8)

(9)

目标散射回波的电压值与场的坐标分解没有关系,在不同极化基分解中有如下关系

(10)

故可得散射矩阵的变换关系为

S(a,b)=US(x,y)UT

(11)

将式(11)代入式(9)中,可得由线极化PSM获得圆极化PSM的变换关系为

(12)

2 系统相位误差对PSM变换的影响

2.1 PSM相位标定原理

目标散射矩阵是一个复矩阵,在理想单站情况下通常可写为

(13)

其中，φ21=φ12,此时消除了矩阵中各元素与距离因子的相关性,可以通过测量PSM幅度相位已知的定标体进行替代法幅相标定。

在进行极化散射特性测量时,当电磁信号在某一组极化发射通道和接收通道中传输时,由于泄露现象的存在,会对另一个极化通道产生影响,形成影响极化测量精度的主要乘性误差。系统发射通道和接收通道存在电磁信号的泄露,加之目标区固有的背景散射,构成了重要的加性耦合误差[12-13]。

实验室中一般化的极化散射测量系统原理如图2所示,按照前文所述,其极化测量误差方程可表示为

Sm=I+RS0T

(14)

式中：Sm为目标极化散射测量矩阵,I为背景极化散射测量矩阵,S0为目标实际PSM,在进行极化散射矩阵定标测量时,需要分别对环境、定标体和目标的各极化组合回波信号进行采集,通过定标体幅度-相位理论值求解复数形式的雷达极化系数矩阵(radar polarimetric coefficients matrix,RPCM),可以实现对目标极化散射矩阵S0的求解[1,12,14],从而实现对测量系统的幅度-相位标定。本文中所采用的目标散射矩阵数据,利用菱形二面角使用单定标体算法获得,其口面正入射及绕雷达视线滚转的极化散射特性可由下式矩阵旋转关系求解[14-16]。

(15)

2.2 系统相位误差来源

假设矢量网络分析仪(或相参雷达系统)的相位测试参考面为图1中所示,实际应用中的测量系统通常会由于收发链路的非理想性而存在不同的相移误差,如放大器、传输线、调制器等的不一致性,这会造成不同极化收发链路间的不对称性,进而影响PSM各元素间的相位一致性。而根据极化散射相对定标误差模型可知,这些相位偏差会被视为电磁波传电长度的路径差引起的,从而使得同一个标准体或目标在不同极化组合通道的高分辨距离像看起来不在相同的空间位置上。假设以S11项测试时系统发生的附加相移δ为参考,则式(13)改写为

(16)

且δ21≠δ12,其中“⊙”为矩阵哈达玛积(Hadamard product),此时运用式(12)进行极化基变换时就会在各极化分量上附加随频率波动变化的误差量,且在正交极化元素求解时会出现矛盾解,无法通过与定标体测量相位的比较进行消除。将式(12)中的S改写成向量模式可得

(17)

将式(16)中对应线极化基的表达方式代入下式,以SLL为例展开可得

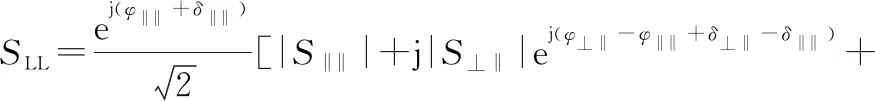
(18)

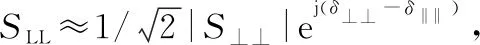
3 宽带相位修正及验证

3.1 宽带相位修正方法

在宽带条件下,可以通过一维傅里叶逆变换获得目标散射中心高分辨距离分布,这是窄带或点频测量时无法获取的目标散射特性信息。对于目标宽带散射矩阵S(ω)来说,可以通过一维傅里叶逆变换获得目标的距离高分辨矩阵。

假设宽带散射矩阵S(ω)的测量带宽为B,一维傅里叶逆变换结果为s(n),对其平移距离单元N得到s(n-N),做傅里叶变换可得

(19)

因为傅里叶变换具有平移不变性,所以由式(19)可以看出,原有矩阵频谱幅度没有变化,只是相位信息发生了偏移,偏移量与其一维高分辨数据的移动位置和带宽相关。基于上述特点,可以考虑借助一维距离高分辨移位的方式,对定标后的目标PSM做进一步的高频相移修正。

3.2 相位修正验证

采用式(12)求解修正后的金属球线极化数据做极化变换处理得到直径300 mm金属球圆极化基下的RCS结果曲线如图6所示。

3.3 实验结果误差分析

(1) 线极化测量结果分析

实验中采用的线极化测量结果使用菱形二面角标定求解获得,为了说明实验数据的可靠性,采用金属球理论计算散射值与测量结果进行比对,分析测试结果的偶发误差。其中金属球散射的幅相理论值通过米氏级数展开求得。对比曲线如图7所示,其偶发误差值统计如表1所列。

表1 测量值与理论值对比(金属球,线极化)

(2) 圆极化合成结果分析

按照类似的方法,可以给出经过极化基变换后,金属球LR和RL两个正交极化分量RCS与理论值的偏差分析。

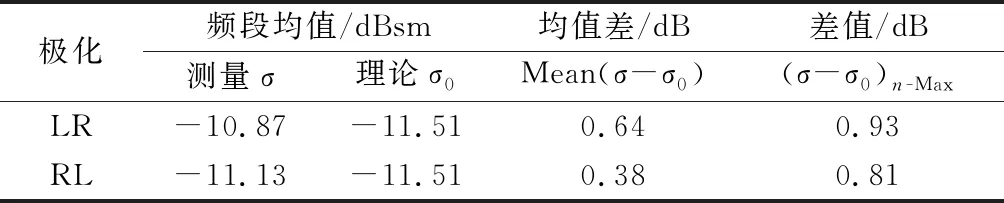
表2 测量值与理论值对比(金属球,圆极化)

4 结 论

本文针对目标极化散射测量技术中,测试系统极化支路的相位不一致性引起测量结果极化基变换错误的问题,由极化基变换原理出发,阐述了极化变换过程中系统高频相移造成极化散射相位标定误差的原因,进而提出了通过宽带高分辨绝对相位对齐修正频域相位偏差的方法,并通过标准体实测数据完成了对方法有效性的验证分析。本方法对提高目标极化散射特性实验室测量精度,提升多通道极化散射测量系统可实现性方面具有较高的实用价值。