毫米波大规模MIMO系统中混合预编码设计

2022-02-23刘仁清曹海燕马智尧陈千鸿

杭州电子科技大学学报(自然科学版) 2022年1期

刘仁清，曹海燕，马智尧，陈千鸿

(杭州电子科技大学通信工程学院，浙江杭州 310018)

0 引言

毫米波大规模多输入多输出(Millimeter-wave Massive Multiple-Input Multiple-Output，MM-MIMO)系统具有很高的通信数据传输能力[1]，预编码技术可以进一步提高毫米波系统频谱效率[2]。然而，传统全数字预编码技术难以实际应用于毫米波通信系统中[3]。为此，文献[4-5]提出一种将数字预编码和模拟预编码相结合的混合预编码方案以实现硬件成本和系统性能之间的平衡。目前，大多数混合预编码主要采用性能较好但计算复杂度较高的全连接结构系统模型(Fully-Connected，FC)[6]，或损失部分性能以换取低计算复杂度的部分连接结构系统模型(Partially-Connected，PC)[7-8]。文献[8]提出发送端为部分连接、接收端为全数字接收的混合预编码方案，通过等效信道的奇异值分解(Singular Value Decomposition，SVD)求得基带预编码器和基带组合器，并以频谱效率最大化为目标依次求得模拟预编码器和模拟组合器，但算法的复杂度太高，实际应用中具有一定的局限性。文献[9]提出一种基于等效信道的全连接结构混合预编码方案，该方案联合设计收发端预编码矩阵和组合矩阵，以最大化等效信道增益为目标，设计模拟预编码矩阵和模拟组合矩阵，对数字预编码矩阵与数字组合矩阵的每一列采用最小二乘准则进行求解，在一定程度上提高了系统频谱效率，但计算复杂度和硬件成本太高。文献[10-11]采用混合连接(Hybridly-Connected，HC)结构系统模型，发送端有若干个子阵，每个子阵内部又是全连接结构，更好地实现了毫米波大规模MIMO系统频谱效率与硬件复杂度之间的平衡。文献[11]提出一种基于连续干扰消除(Successive Interference Cancellation，SIC)的混合连接结构混合预编码方案，将频谱效率优化问题分解为多个子速率优化问题，通过每个子速率中等效信道的奇异值分解得到最佳混合预编码子矩阵，并取其相位信息和恒模约束从而得到模拟、数字预编码子阵，最后交替迭代求得模拟、数字预编码矩阵。该算法需要将数字预编码矩阵设置为对角阵且只适用于发送端数据流数与射频(Radio Frequency，RF)链路数相等的情形，具有一定的局限性。本文对文献[11]方案进行改进，提出一种基于等效信道增益最大化的混合连接(Equivalent Channel Gain Maximization-Hybridly Connected，ECGM-HC)混合预编码方案，既不需要约束发送端数据流数与RF链路数相等，也无需将数字预编码矩阵设置为对角阵形式，具有更优的性能和更广泛的适用性。

1 系统模型和信道模型

1.1 系统模型

图1 混合连接结构毫米波大规模MIMO系统

x=FRFFBBs

(1)

接收信号为：

(2)

式中，ρ为平均接收功率，H∈CNr×Nt为信道矩阵，n～CN(0,σ2)表示高斯分布信道噪声向量。

1.2 信道模型

假设信道状态信息(Channel State Information，CSI)已知，由于毫米波信道的有限散射特性，传统的信道模型不再适合毫米波信道，因此本文采用扩展的S-V(Saleh-Valenzuela)信道模型[12]：

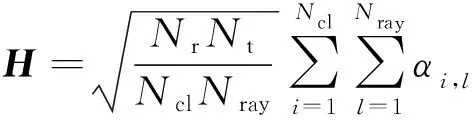
(3)

(4)

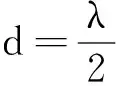
2 混合连接结构的混合预编码设计

毫米波大规模MIMO系统的频谱效率为[13]：

(5)

令HFRF=He，式(5)重写为：

(6)

信道矩阵H=[H1,H2,…,HM]，其中，Hi∈CNr×Nt_i,i=1,2,3,…,M，则有He=[H1FRF,1,H2FRF,2,…,HMFRF,M]，以等效信道He增益最大为目标来设计FRF：

(7)

式中，tr(·)为矩阵的迹，可转化为：

(8)

求得模拟预编码矩阵FRF后，将数字预编码矩阵FBB分解为Ns列向量的组合FBB=D=[d1,d2,…,dNs]=[DNs-1dNs]，此时系统的频谱效率表示为：

(9)

(10)

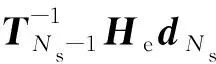
(11)

进一步令：

(12)

频谱效率最终表示为：

(13)

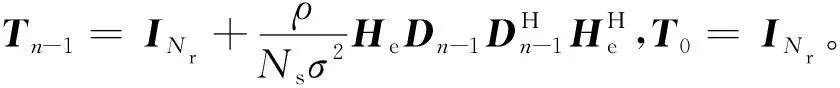
(14)

(15)

(16)

混合预编码矩阵F=FRFFBB。

3 复杂度分析

4 仿真实验结果与分析

表1 仿真实验参数

由于文献[11]要求数据流数与射频链路数相等，故在Ns=NRF=8，Nr=16，M=4，NRF_1=,…,=NRF_M=2时，分别采用最优全数字预编码方案、本文所提基于ECGM-HC混合预编码方案、文献[11]中基于SIC-HC混合预编码方案、纯模拟预编码方案进行仿真实验，得到频谱效率与信噪比的关系如图2所示。从图2可以看出，随着信噪比的增大，4种方案的频谱效率均逐渐增大，最优全数字预编码方案性能最佳，纯模拟预编码方案性能最差；在信噪比为10 dB时，本文提出的基于ECGM-HC混合预编码方案频谱效约为45.0 bps·Hz-1，优于文献[11]中基于SIC-HC混合预编码方案的42.5 bps·Hz-1，更接近最优全数字预编码方案。

图2 系统频谱效率与信噪比的关系

当射频链路数与发送数据流数不同，即Ns=8，NRF=16，Nr=16，M=4，NRF_1=,…,=NRF_M=4时，本文所提方案、最优全数字预编码方案、纯模拟预编码方案的频谱效率与信噪比之间关系如图3所示。从图3可以看出，和文献[11]方案相比，本文所提方案的性能接近最优全数字预编码方案。文献[11]方案只适用于射频链路数与发送数据流数相等的情况，而本文方案不受射频链路数与发送数据流数相等条件的约束，适用性更广。

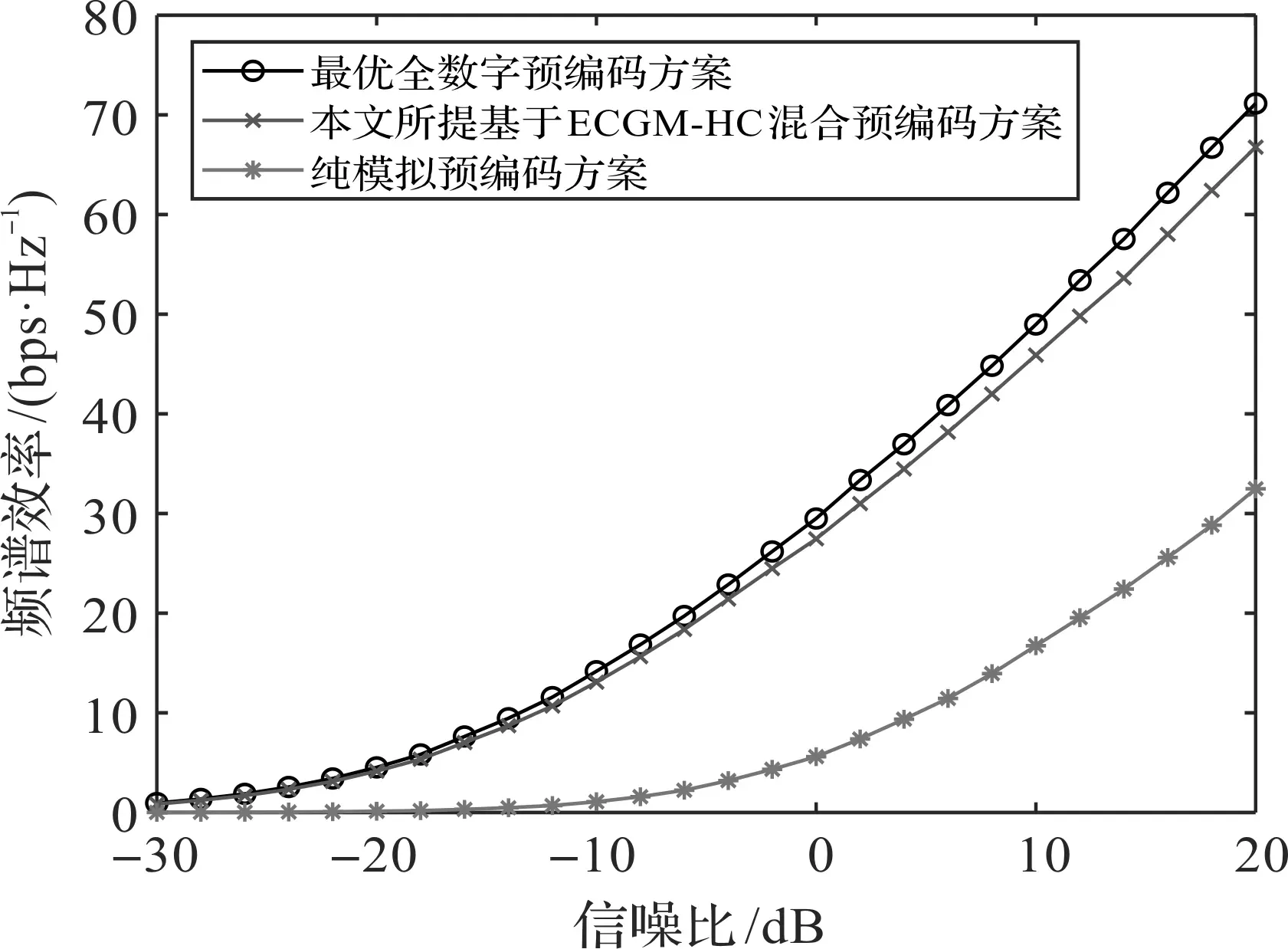
图3 系统频谱效率与信噪比的关系

SNR=1 dB，Ns=NRF=16，M=4，NRF_1=,…,=NRF_M=4时，4种预编码方案的频谱效率和接收天线数之间的关系如图4所示。从图4可以看出，随着天线数的增加，4种方案的频谱效率均增加，当接收端天线数为38根时，本文所提方案的频谱效率约为43.5 bps·Hz-1，优于文献[11]方案的37 bps·Hz-1。

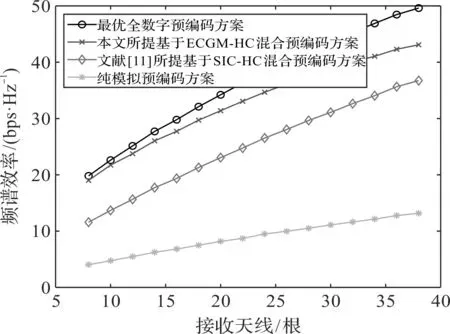
图4 系统频谱效率与接收天线数的关系

Ns=8，Nr=16，NRF=16，M=4，子阵中RF链路数(NRF_1,NRF_2,NRF_3,NRF_4)分别为(4，4，4，4)，(2，6，6，2)，(2，3，5，6)，(1，7，7，1)时，本文基于ECGM-HC混合预编码方案、最优全数字预编码方案、纯模拟预编码方案的频谱效率与信噪比之间的关系如图5所示。从图5可以看出，本文基于ECGM-HC混合预编码方案的4种子阵结构均接近最优全数字预编码方案，系统频谱效率R(4,4,4,4)>R(2,6,6,2)>R(2,3,5,6)>R(1,7,7,1)，即当各子阵中RF链路数相等时，系统性能最优。