考虑大陆引水的海岛地区复杂水工程群多目标优化配置研究

于欣廷，郭玉雪，许月萍

（浙江大学建筑工程学院，杭州310058）

0 引言

随着社会和经济的快速发展，水资源供给和需求之间的矛盾越发突出。在21世纪初，我国的缺水现象已逐渐显现，全国有2/3 的城市均存在供水明显不足的问题，水资源在时间和空间上分布极不均匀［1］。海岛与同纬度大陆地区相比，存在降水量少、蒸发量大且地形地貌特殊等条件，导致可利用的地表水资源量较少，再加上地下水赋存条件差等问题，致使海岛地区淡水资源极度缺乏［2］。因此对海岛地区有限的水资源进行优化配置以实现高效利用，具有非常重要的意义，也是亟待解决的问题［3］。

从本质上来说，水资源优化配置是一个高度复杂的风险决策问题［4］。早在20世纪中期，国外就开始研究水资源优化配置问题，具体起源于Masse 首次提出了水库优化调度问题并基于此类问题展开了研究［5］。近些年学者们主要从模型构建、优化智能算法、在不确定性中确定科学决策方法等方面对水资源配置问题进行了分析和研究。模型优化中通常结合经济因素或生态因素以更加科学地进行水资源配置，其中Zhang 等［6］利用可视化、交互式的多目标分析方法基于引水边际效益最大、供水保证率最高、缺水量最小等目标确定了相应的跨流域引水工程规模；Dai 等［7］提出了基于基尼系数的随机优化模型，将水文模型、水资源模型、基尼系数以及机会约束规划集成到支持流域水资源分配的多目标优化建模框架中以平衡各目标之间的矛盾；Martinsen 等［8］提出一种用于联合优化水量分配和水质管理的水力经济模型，平衡了海河流域地下水支和流域供水成本的经济效益。针对水资源分布时空不均衡的问题，学者们基于跨流域调水提出相应的适用模型，Yu 等［9］结合了投影寻踪模型和灰狼优化方法，提出了跨流域水资源优化配置模型，并在中国松花江流域验证了该模型的可行性和合理性；郭玉雪等［10］考虑南水北调东线工程供水目标，构建了江苏段水资源优化调度模型并提出了一种改进的多目标蛙跳算法，有效地缓解了供水与抽水的矛盾。为处理复杂水资源系统问题，Khosrojerdi 等［11］提出具有2 类隶属度函数的两阶段区间参数随机模糊规划，在不确定性下将水资源以最优形式分配给不同的用户；Harken［12］利用统计假设检验和综合方法来规划水资源网络特征，提出了框架工作模型以在水资源优化配置中建模预测和决策；骆光磊等［13］提出一种水库群运行自适应矩估计改进深度神经网络模拟方法；谭倩等［14］基于鲁棒优化方法建立了水资源多目标优化配置模型。王浩［15］提出在跨流域大系统中通常涉及的水库群系统内部具有关联性和补偿性，使得调度管理能够从流域整体出发，充分开发利用水资源，提高水资源利用率。综上所述，目前国内外对水资源优化配置有较多研究，并在众多地区构建适用模型获得较好的应用效果，但海岛地区水资源配置的相关研究甚少，未能考虑到海岛地区的特点以及需结合大陆引水工程以满足自身需水的前提；对配置中的需水用户，大部分研究侧重平衡各用户间的矛盾［11，16］，但实际上需水用户之间可能存在水力联系，这种联系可补偿由于供水路径限制而导致供水保证率计算偏低的问题；针对经济效益优化方面，大多数研究仅将经济效益作为目标函数之一，通常侧重经济用水带来的效益，比如发电效益［17，18］，却忽略了供水过程中产生的成本支出。

本文基于目前的研究情况，为解决海岛城市水工程复杂、供水效率低下问题，提出适用于海岛地区的水资源优化配置方法。基于“分区分级”的优化配置理念，明确各区域内以及区域间的水力联系，且将水厂余蓄量的概念引入配置模型的构建，尽可能提高水库供水的效率，最终构建适用于海岛地区的复杂水工程群多目标优化配置模型。

1 理论与方法

1.1 “分区-分级”优化配置理念

基于海岛地区水工程群的复杂性，为更好地建立优化配置模型，需采用科学的方法对系统进行分析概化。首先获取水库、泵站等复杂水工程群的基本特性和分布位置、水厂的各项基本参数、输水方式和管道等；结合各水工程群的地理位置，对整个复杂水资源系统进行区域划分，明确各水库、水厂、泵站之间的水力关系，完成“分区”过程；海岛地区的农业灌溉用水大多来源于水库的固定供给以保证农业需求，而生活用水、工业用水等大多来源于水厂供水，因此在水资源优化配置中可将水厂概化为需水部门，以水厂向用水户的供水量作为配置系统中的需水部分参与计算，进一步结合水厂的特性建立“分级”模式，第一层级仅考虑独立水厂的供水保证率，此种类型的水厂与其他水厂没有联动作用，无法依靠其他水厂的水量补充以满足供水需求；第二层级考虑联合水厂，即与其他水厂有联动作用的水厂，此类水厂可以通过水量的互补以实现最大程度满足供水保证率，以此改善水库供水对象固定的约束条件，在计算供水保证率时可以将各水厂的需水量总和综合考虑。

1.2 考虑大陆引水的优化配置模型

由于海岛城市的淡水资源缺乏，需在水资源配置的过程中考虑大陆引水的重要作用。本研究基于本岛水库蓄水、大陆引水等多水源多用户的前提下实现多目标优化的实际问题展开，确定优化配置模型的决策变量为不同水源向不同水厂的供水量以及额外从大陆引水的水量，xij为i水源向j水厂的总供水量，I是水源的个数，J是指用水户，即水厂的个数，单位为m3。配置周期为年尺度，配置单元为日尺度。

1.2.1 目标函数

不同于内陆地区的常规水资源配置，海岛地区优化配置模型的建立需结合海岛的供水特性以及经济发展目标。同时，为尽可能提高水库供水的效率，本文将水厂供水余蓄量概念融入到优化模型。水厂余蓄量特指配置期间内各水库将水输送至水厂，水厂根据当月供给需求，向需水用户供水，余下的水暂时存蓄在水厂中，若次月仍在配置期间内，则可补偿次月的水厂供水需求；若本月为配置期末时段，则余下的水量只能存蓄在水厂中，在此配置周期内未能实现真正意义上的供水。考虑水厂供水余蓄量，本文确定配置目标为供水保证率最大化、经济成本最低化以及水厂供水余蓄量最小化。其中供水保证率的主体对象为水厂，指能够满足水厂需水的程度（即需水量的百分比）；经济成本指在供水过程中产生的成本支出；供水余蓄量为在供水单元内各水库向各水厂的供水量若超过实际需水量时，则有部分水量存余在水厂中，在整个配置周期内的总和即为余蓄总水量。各目标函数具体如下所示：

目标函数1——水厂供水保证率最大：

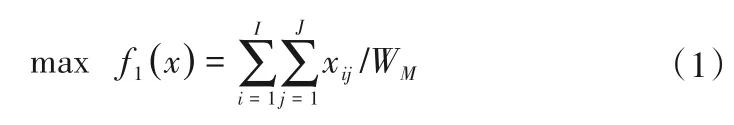
式中：WM为各水厂在年内按照日常供水需求所需支配的水量总和，m3；M为水厂序号，若包含一级水厂和二级水厂时，则需分开计算一级和二级水厂的供水保证率。

目标函数2——净成本最低：

在计算过程中，将成本支出Cc分为两部分分别计算，一部分为本岛供水产生的成本支出Cic，元；一部分为大陆引水产生的成本支出Cmc，元；成本支出为调度系统运行一年内各水库以及泵站工作产生的成本总和。

目标函数3——水厂余蓄量最低：

式中：Wsw为在最终存蓄在水厂中，未能供水到需水用户的部分水量，即余蓄量，m3；Was为各水厂向需水用户的实际总供水量，m3。

1.2.2 约束条件

针对研究区域供水能力、泵站抽水能力以及管道输水能力设定相应的约束条件，基于大陆引水工程的承载力以及政府相关规定要求设定各类供水源的取水上限约束，模型的约束条件包括以下六个方面：

（1）水量平衡约束。

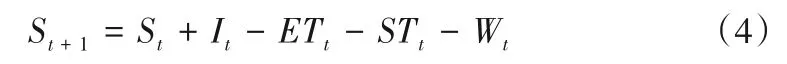
式中：St+1、St分别为水库的时段初、末蓄水量，m3；It、Wt为时段水库的入流量和出库流量，m3；ETt、STt分别为蒸发和渗漏量，本研究中假设蒸发和渗漏量可忽略不计，m3。

（2）水库可供水量约束。

式中：Wi为i水源的当前水库的可供水量（考虑在当前时段的入库径流量以及出库流量），m3。

（3）泵站过流能力约束。

（4）管道输水能力约束。

（5）本岛供水以及大陆引水量约束。根据当地政府对水资源开发利用程度规划以及引水工程上限能力等各相关依据，确定一年内总取水量的上限值以及大陆引水总量的上限值。

（6）变量非负约束。

1.3 水工程群联合调度成本计算

鉴于目前大多数研究仅将经济用水的效益作为目标函数之一，较少有研究关注供水过程中的成本，本文提出的配置模型考虑了海岛供水过程中的具体成本支出。海岛城市水源包括本岛水和大陆水，其单位取水量的成本由于供水方式和供水距离的不同而产生差异，为更好地优化供水结构，需对成本进行详细精确的计算以实现经济效益的提升。水库群在供水过程中的成本计算方法详述如下。

1.3.1 取用本岛水的成本支出

本岛水取用的成本计算包括3个方面，一是水资源费，是指对城市中取水的单位征收的费用，这项费用，按照取之于水和用之于水的原则，纳入国家及地方财政，作为开发利用水资源和当地水资源系统管理的专项资金［19］，具体的单价要根据当地政府的相关规定来确定。二是水费，即从水库中取水所需要交纳的费用，此部分费用分为年度收费和按取水量收费两种方式。三是在取用本岛水的过程以及运输过程中利用泵站抽水时，泵站工作所消耗的电费。具体计算公式如下：

（1）水资源费。

式中：k为水资源费的单价，元/m3。

水资源费即水资源费单价与所有水库向水厂的供水量总和相乘。

（2）水费。

式中：ci为水库的单价水费，元/m3。

水费支出为水费单价与相应水库的供水量相乘。

（3）泵站工作消耗产生的电费。

式中：di为单位电价，元/kWh；N为泵房中设备的数量；为泵房中第n号设备的配套电机功率，kW；为泵房中第n号设备的最大流量限制值，m3/s；为经过u泵站的流量值之和，m3。

1.3.2 大陆引水的成本支出

从大陆引水的成本支出主要也分为3个部分：水资源费、水费以及从大陆引水过程中泵站工作产生的电费。从大陆引水的水资源费和水费的计算公式如下：

式中：Xml为从大陆引水的总量，m3；m为从大陆引水需要交纳水资源费的单价，元/m3；n为从大陆引水需要交纳水费的单价，元/m3。

大陆引水水源需经过较长一段的运输路线才可实现对海岛城市供水，因此需额外计算泵站工作以支撑大陆引水完成跨海运输所需要消耗的总电量。

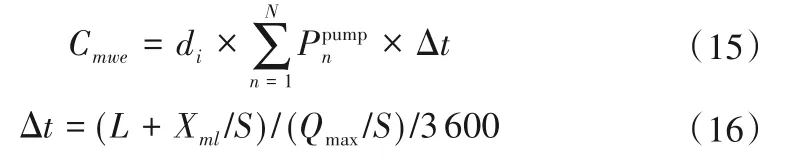
式中：di为单位电价，元/kWh；为泵房中第n号设备的配套电机功率，kW；Δt为大陆引水完成跨海运输所需要的时间，h；L为引水隧道的管道长度，m；S为引水隧道的管道横截面积，m2；Qmax为引水隧道中的最大过流能力，m3/s。

1.4 多属性决策方法

多属性决策（Multi-attribute decision making with finite alter⁃natives，MADM）通常指问题中的决策变量为离散分布，即待选方案数量有限，需要对各待选方案进行评价和优选［20］。优选过程通常涉及对某一项“指标”的评价，指标是指决策者主观赋予评价对象的判断依据，或是决定待选方案优劣的评价标准［21］。本文基于组合赋权、主客观结合的多属性决策方法对优化配置后的方案进行分析排序，采用层次分析法确定各指标的主观权重，采用信息熵权法确定客观权重，然后采用线性加权平均方法得出组合权重，作为各指标重要程度的判别依据。

层次分析法（Analytic Hierarchy Process，AHP）是20世纪中叶Saaty 提出的一种数学分析方法［22］。与凭借主观判断法和定量分析法相比较，层次分析法以量化与非量化相结合的方式来评价影响决策的指标而更加有优势。通过对目标层、准则层以及决策层的分解，以经验判断和定量的计算评估各个准则对决策层贡献权重的大小［23］。熵权信息法，根据熵的定义，熵是用来描述在某一给定时刻一个系统可能出现的有关状态的不确定程度。它是物质系统状态的一个函数，表示系统的紊乱程度，是系统无序状态的度量［24］。对于某项指标，可以用熵值来判断某个指标的离散程度，其信息熵值越小，指标的离散程度越大，该指标对综合评价的影响（即权重）就越大，如果某项指标的值全部相等，则该指标在综合评价中不起作用。

主客观组合赋权方法主要分为加法合成法、乘法合成法、极差最大化组合赋权法和基于客观修正主观的组合赋权方法等四种典型方法［25］。其中加法合成法是目前较为通用且能够直观反应主客观权重对最终决策方案的影响程度的方法。本文采用加法合成法来直观反应主客观权重对最终决策方案的影响程度：

式中：Wθ代表指标最终权重值；Wθ_obj代表各指标的客观权重值；Wθ_subj代表各指标的主观权重值；λ为权重系数。

2 研究区域概况

本文以浙江省舟山市为例进行海岛地区复杂水工程群多目标优化配置研究。由于背靠长三角的广阔经济腹地，也是我国海运的“T”型交汇要冲，舟山群岛新区成为我国第四个国家级新区。舟山市人均水资源量618 m3，不到全国人均水平的1/3，属于资源性缺水地区［26］。舟山市全市与大陆分隔，水资源几乎全部依赖降水补给［27］。历来干旱缺水是舟山市主要的自然灾害，并造成了巨大的经济损失，且近些年舟山市的用水总量呈不断上升的态势，因此供需严重不平衡，制约了当地的社会经济发展。

本文基于舟山26 个水库、4 个水厂展开研究，将水厂概化为需水用户。依据工程要素信息，确定在运输过程中共涉及15个泵站参与工作。按照“分区分级”理念，分析各水库与水厂之间的水力联系，以水厂为核心，根据各水库及水厂的地理位置，将舟山本岛划分为三个区域，分别是岛北片区：以岛北水厂和临城水厂为供水中心；虹桥片区：以定海水厂为供水中心；东部片区：以平阳浦水厂为供水中心。其中岛北水厂为独立水厂，设定为一级水厂，临城水厂、定海水厂以及平阳浦水厂为联动水厂，因此将3 个水厂的供水保证率合计考虑，设为二级水厂，即将岛北水厂供水保证率和三厂合计供水保证率分别计算，以此作为评判标准。各要素及水力联系的区域概化如图1所示。

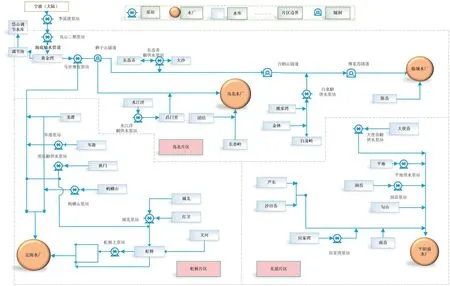
图1 舟山本岛水力关系概化图Fig.1 Generalized diagram of hydraulic relations of Zhoushan island

收集研究区域各种数据，包括工程基础数据信息、优化模型的输入数据。其中，本岛内5 个较大的水库特征参数如表1所示。水库可供水量的确定依据各水库的入库径流量，结合各水库在配置初始时刻的蓄水量，确定水库在配置期内各单位时段下的可供水量。水厂需水量的确定则依据在配置期间内4个水厂各自的需水量。

表1 研究区域主要大型水库数据信息Tab.1 Major large reservoir data information of study area

3 结果与分析

3.1 优化配置模型分析验证

选取各项资料及数据均完整的2016年作为优化模型的验证年份。调查获取2016年舟山本岛实际数据，基于本文提出的考虑大陆引水的海岛地区复杂水工程群优化配置模型对舟山本岛水资源优化配置进行实例计算。经过众多学者验证［28，29］，NSGA-Ⅱ算法计算效率较高，且对优化模型的目标函数与约束条件的形式不做要求。本文采用带有精英保留策略的快速非支配多目标优化算法（NSGA-Ⅱ算法）对模型进行求解，以实现全局范围内搜索最优解，从而避免传统方法的计算精度低、过早收敛等问题。设定算法的各项参数：种群数量n=250；交叉概率Pc=0.9；变异概率Pm=0.01；迭代次数num=1 000。

经过不断迭代搜寻最优解得到Pareto前沿。以岛北水厂供水保证率、三厂合计供水保证率、供水成本为x、y、z轴，供水后水厂中的余蓄量为颜色标记，绘制Pareto解集四维图，如图2（a）所示。红色图块为按照2016年实际供水实现的供水保证率和相应成本支出。经分析可知在优化配置后成本有明显的下降趋势。当岛北水厂以及三厂合计的供水保证率均达到99%以上时，成本支出可以控制在［3 514.09，4 035.11］万元范围内，相较于2016年的理论供水成本4 125 万元，可平均降低300 万元。2016年的实际供水方案中大陆引水占供水总量的34.9%，而经过优化后的大陆引水占比可平均下降至29%。因此本研究提出的优化配置模型可以提高本岛水源在供水过程中的比例，降低大陆引水的比例，提高本岛水资源的利用效率，进而降低供水过程的成本支出。但由于实际调度中尚不能获得未来水资源状况，而优化调度过程中未来可供水情况为已知条件，因此对比的结果可能存在一定偏差。在实际应用中，若可以和中长期水文预报相结合，预测未来的来水情况，则可进一步优化供水过程，协调本岛水和大陆水的供水比例。

为进一步分析Pareto 前沿上特性的变化趋势，本文对三维坐标下的数据点进行二维投影。如图2中的（b）所示，以岛北水厂、三厂合计供水保证率为x、y轴，颜色标记表示供水成本。当四个水厂的供水保证率均趋于100%时，供水成本有着明显的上升趋势；而当成本维持在较低水平时，相应地岛北水厂和三厂合计的供水保证率也都处于较低水平。如图2中的（c）所示，以三厂合计供水保证率、供水成本为x、y轴，颜色标记表示余蓄量。供水保证率和供水成本之间呈显著的负相关关系，而余蓄量则随着供水保证率的提高呈现先增加后下降的趋势。这是由于水厂需水量在配置期间内呈动态变化，在调度单元内若当月的水厂需水量处于较低水平，则水库供水未完全输送至需水用户，进而造成余蓄量的增加；随着供水保证率逐渐接近100%时，水库向水厂输送的绝大部分水量均供给需水用户，因此余蓄量呈下降趋势。从降低余蓄量的角度考虑，供水保证率在70%～85%范围内的方案最不适宜采用。综上所述，本文提出的海岛地区水资源配置模型在多目标、多约束条件下，基于本岛水和大陆引水的单位供水成本差异性，同时考虑水厂余蓄量的最小化目标，可以实现合理优化供水结构，协调本岛水和大陆水的供水比例，有效提升经济效益，具有实际参考意义和价值。

图2 图2 2016年实例计算结果各指标分布示意图Fig.2 Schematic diagram of each index distribution of example calculation results in 2016

3.2 典型年优化配置结果及多属性决策

3.2.1 典型年优化配置结果

为验证模型在不同来水情况下能否对海岛地区水资源进行合理有效的优化配置，本文对舟山本岛的长系列历史径流资料进行收集分析，确定丰水年（25%）、平水年（50%）以及枯水年（75%）共3 个典型水平年，以年为配置周期，以月为配置单元，将各水库在不同典型年下的入库径流量作为数据输入，采用多年需水平均值作为各水厂的需水量，对不同来水条件下的舟山本岛水资源优化配置展开研究并对配置结果进行分析。

采用NSGA-Ⅱ算法对模型进行求解，迭代1 000 次后得到对应典型年的Pareto 前沿，如图3所示。总体来说，随着来水量不断减少，供水成本与之呈现负相关关系，这是由于优化模型通过调整本岛取水和大陆引水的比例以满足水厂的实际需求，考虑到大陆引水单位成本高于本岛水源，导致成本支出将呈现整体上升趋势。在不同典型年下，随着供水保证率提高，余蓄量呈先增加再降低的变化趋势，最少可实现零余蓄量，最多可达到500 万m3的余蓄量，水厂需水量在配置期间呈动态变化，在配置单元内若水库供水量与水厂需水不对等则会产生余蓄水量，进而造成在余蓄量的累积以及供水保证率的下降，这种类型的方案在实际中并不可取。

进一步分析不同典型年下本岛供水和大陆引水的供水比例关系。将经过优化后的非劣解集对应的本岛供水比例、大陆引水比例以及总的供水保证率进行对比分析，见图4。随着来水量逐渐减少，供水保证率的变化范围逐渐增大。在丰水年，本岛水源作为主要供水源；在平水年，本岛供水比例略有下降，同时大陆供水比例有小幅度提升；随着来水量进一步减少，在枯水年，由于本岛各水库的来水量很少，必须依靠大陆引水以满足本岛的需水，有部分解集以大陆引水为主要供水源，此种类型供水方案的成本相对较高，在实际中可能不会被优先采纳，但在本岛水源库存量告急且预报未来仍持续干旱的情况下，优先使用大陆引水则是较优选择，因此大陆引水在干旱时期占有非常重要的地位。当来水条件一定时，本岛水源和大陆水源的不同供水比例组合与供水成本有着显著相关关系。本岛供水为主要水源时的供水成本比大陆引水为主要水源，本岛水为辅助水源的情况下要低，说明提高本岛水源的利用效率可以有效降低供水成本，有助于社会、经济的协调发展。

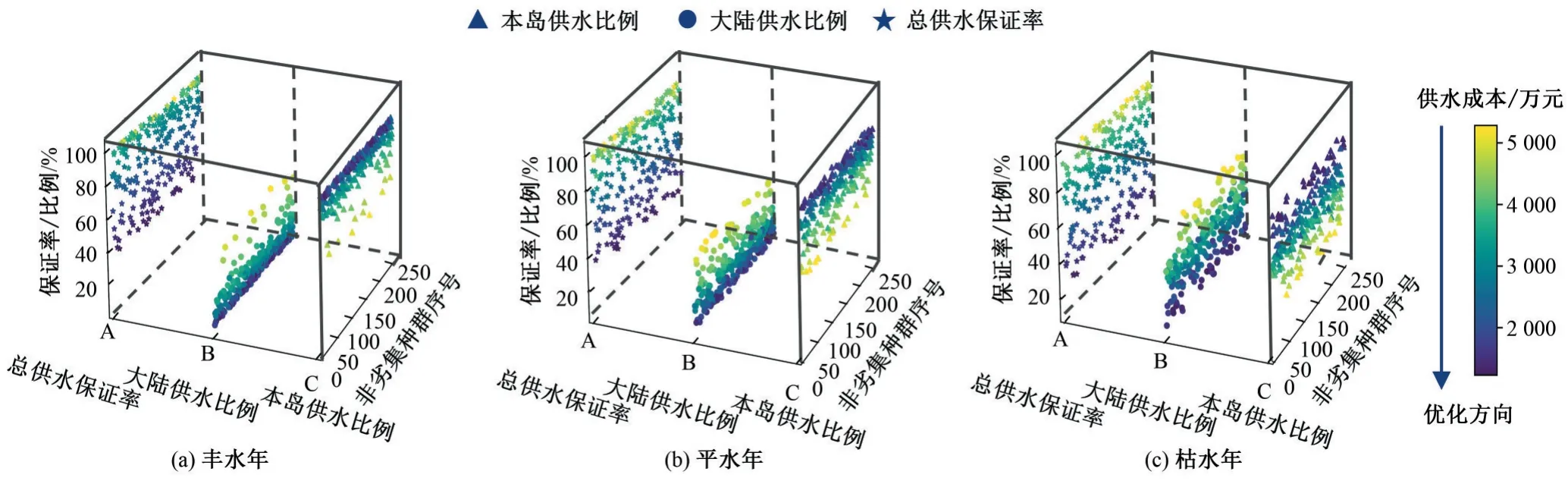
图4 3种典型水平年优化配置后的非劣解集对应的本岛供水比例、大陆供水比例及总供水保证率的对比图Fig.4 Comparison of the proportion of water supply of the island，the proportion of water supply of the mainland and the guarantee rate of total water supply in the non-inferior solution sets after three typical level years'optimal allocation

3.2.2 多属性决策结果及方案分析

水库群多目标调度决策作为一个多维的、非线性的、连续的多目标决策问题［30］。以舟山本岛跨流域调水不同典型水平年的优化配置结果为基础，对得到的非劣解集进行分析，采用基于主客观组合赋权的多属性决策方法确定各方案的优劣，以协助确定不同配置方案适合的应用场景，为决策者提供科学参考依据。

根据3.2.1 中的模型优化结果，选定4 个目标函数作为多属性决策中的评判指标，分别是岛北水厂供水保证率、三厂合计供水保证率、成本以及水厂余蓄量。首先对Pareto 解集进行初步筛选，考虑到实际配置过程中水厂的供水保证率不能过低，缺水程度较高会严重影响人们的正常生活，不利于经济、社会的发展，因此候选方案在供水保证率80%以上的解集中选取；再对各解集中的数据进行预处理实现归一化后，采用熵权信息法获得各指标的离散程度，评判其在综合评价中的影响，计算不同典型年下各指标的客观权重值（OW）：丰水年［0.147，0.141，0.252，0.460］；平水年［0.143，0.152，0.145，0.560］；枯水年［0.104，0.091，0.126，0.679］。

按照以下5种决策偏好设定各典型水平年对应的五种主观权重矩阵：①优先考虑整体供水保证率最大化；②优先考虑岛北水厂供水保证率最大化；③优先考虑三厂合计供水保证率最大化；④优先考虑成本最低；⑤均衡考虑供水保证率和成本最优化。不同主观权重矩阵可以展示决策者在对各方案进行评价时的偏好。根据权重矩阵推算出四个指标权重分布如图5（a）所示，其中S1-S5 指代上述五种偏好，OW 指代各指标的客观权重分布。其中S1、S2、S3 供水保证率指标的权重占比处于绝对优势，S4 中的成本指标则占较大权重，S5 中各指标所占权重值为相对均衡状态；相比于主观权重，客观权重的分布较统一，岛北水厂供水保证率、三厂合计供水保证率以及成本3个指标的权重占比基本一致，水厂余蓄量的客观权重几乎占据一半以上，这说明水厂余蓄量的数据分布较为离散，更容易影响综合评价的结果，而其他3 个指标值分布范围较为集中。设定组合系数λ=1/2 对主客观权重进行线性加权，由图5（b）所示。线性加权后指标4（水厂余蓄量）的占比有明显上升，而供水保证率及成本部分的权重占比相应缩减。

图5 3种典型水平年下基于5种决策偏好的权重值展示Fig.5 Weight values of three typical level years based on five decision preferences

将典型水平年优化配置结果基于组合赋权的多属性决策方法，按照五种不同的偏好类型确定主观权重，再结合客观权重值进行线性加权平均，获得各指标的最终权重值。依据权重值得到不同情况下的优选方案，各方案的指标值如图6所示。

图6 3种典型水平年在不同权重类型下最优方案的指标参数对比图Fig.6 Indicator parameter comparison chart of the optimal scheme under different weight types of three typical level years

由图6可知，在决策偏好的引导下，基于不同指标的优先考虑级别，赋予不同的主观权重矩阵以适应不同的应用场景。如S1方案能实现整体供水保证率最大化，但此时成本支出相对较高，余蓄量处于较高的水平，因此当优先考虑成本最优化或余蓄量最低时，S1 方案应首先被淘汰；但当优先考虑整体供水保证率的最优化时，S1 方案可以作为最优候选解以供参考；S2 方案和S3方案分别更侧重于岛北水厂、三厂合计供水保证率的满足，因此当舟山市优先考虑各水厂的供水保证率，而对降低成本的需求不高时，可以考虑S1、S2 和S3 方案；其中当对余蓄量指标的最优化也同样纳入决策考虑时，应优先考虑S2 方案；当优先考虑成本最优化时，S4 可以作为最优候选解；相较于前四个方案，S5方案在供水保证率和成本降低以及余蓄量等各项指标的优化中体现较为均衡的状态，因此当供水资金不充足且对供水保证率要求不高的情况下，并且希望最大程度减少水厂余蓄量时，S5为五组方案中最理想的配置方案。不同决策偏好获得的配置方案随着来水量的变化有着明显的变化趋势。随着来水量减少，供水保证率随之下降，而成本则逐渐增高，但水厂余蓄量与来水量变化没有明显的相关性；根据方案结果可发现来水量与本岛供水比例呈现正相关关系，与大陆引水比例呈负相关，在3 种典型年下，S4 方案中的本岛供水比例占比最大，大陆引水占比最小，说明当本岛水资源得到充分利用时，可以有效降低成本支出。在实际调度中依据多属性决策方式，有助于科学分析优化后的调度方案，明确不同方案各自的优劣，以辅助决策者在不同场景下按需选取更适用的方案，提高优化调度的实际应用意义。

4 结论

本文针对海岛地区复杂水工程群系统，提出了一种新的适用于海岛地区的水资源优化配置方法。基于“分区分级”优化配置理念，分析了多水源多用户复杂系统中的水力联系，并以供水保证率最大化、成本支出最小化以及水厂余蓄量最小化为目标函数，构建了复杂水工程群多目标优化配置模型，并应用于浙江省舟山本岛的水资源优化配置。主要结论和存在的不足如下：

（1）2016年实例表明本文提出的海岛地区水资源优化配置模型可有效提高本岛水的利用效率，协调优化本岛水与大陆引水之间关系，通过降低水厂余蓄量以提升水库供水的有效性，最大程度提高供水保证率，同时降低供水过程中的成本支出。

（2）基于“分区-分级”配置理念建立的复杂水工程群多目标优化配置模型可以在不同来水情况下做出合理响应，在丰水年、平水年和枯水年3种不同典型年来水条件下，优化调度方案可以充分利用本岛水源，本岛的供水比例平均为85.46%、77.16%和61.67%，通过不断调整本岛水和大陆引水的比例，在满足供水保证率情况下尽可能降低成本，实现经济效益的提升。

（3）基于层次分析法获得的主观权重和熵权信息法获得的客观权重，通过组合系数赋权可以均衡主观影响程度，以辅助科学决策，使优化后的配置方案应用在不同场景。

（4）在实际应用中若能结合中长期预报结果，则优化模型可实现从全局角度提高水资源调度的有效性，协调分配多水源的供水比例，平衡水源与需水用户之间的矛盾；且可根据水源的周期性变化，探讨大陆水源与本岛水源的可供水量变化关系，以更好地提高经济效益。□