基于HLLC近似Riemann求解器的天然河道水流运动模拟
2022-02-23孙万光杨海滔杨斌斌范宝山
孙万光,杨海滔,杨斌斌,房 巍,范宝山
(1.中水东北勘测设计研究有限责任公司,长春130061;2.水利部寒区工程技术研究中心,长春130061;3.辽宁省河库管理服务中心(辽宁省水文局),沈阳110003)
0 引言
天然河道一维非恒定流数值模拟在水利规划设计以及防洪减灾等领域应用十分广泛。天然河道特别是山区性河道断面几何形状快速变化、河底比降变化大,水流流态可能出现急流、缓流交替现象;另外,高纬度严寒地区江河冰塞及冰坝现象频繁发生,冰坝溃决后坝下将出现激波间断,这些都属于浅水间断流动。因间断处水力要素突变,具有较强非线性,传统数值计算方法(如有限差分)往往失效[1]。
对于间断问题,控制方程上,Lax[2]证明了守恒数值格式的解可收敛至守恒控制方程的弱解。Hou[3]证明了采用非守恒型控制方程求解间断问题将会得到错误结果,这些方程仅对光滑流动有效,对于间断问题,根据跳跃条件计算出的激波波速是错误的。数值计算方法上,Godunov[4]格式因具备较强的不连续问题处理能力而广受欢迎[5-8]。在Godunov 格式下,将齐次浅水方程组的Riemann 问题定义为具有分段变量恒定的初值问题,采用精确Riemann 求解器[9]可求得单元界面处的通量值,精度高,但需要对非线性代数恒等式进行迭代求解,增加了计算资源的消耗[10]。为了简化计算,多种近似Riemann 求解器得到快速发展,如Roe 法[11]和HLL 法[12]等。Roe 线性化Riemann 求解器缺点如下[10]:①在跨临界流或激波模拟中,为避免非物理解必须进行熵修正;②在强稀疏波作用下(水流非常浅的区域),线性化Riemann 求解器计算水深出现负值;③在强波相互作用下,线性化Riemann 解一般缺乏鲁棒性。HLL 近似Riemann 求解器将波族简化为2 个,只适用于具有2 个方程的一维系统[10],对接触间断和剪切波模拟精度较差。基于2 波族的HLL 近似Riemann 求解器,Einfeldt 提出了波速的计算方法,这被称作HLLE[13]求解器,之后又进一步将HLL 求解器单个中间状态修改成线性分布状态,称作HLLM[14]求解器,特定参数条件下,HLLM 求解器降为线性化Roe 求解器。为了恢复HLL 求解器缺失的波族,Toro[15]提出了HLLC求解器,为3波族模型,可准确求解接触间断和剪切波问题[16]。Alireza[17]采用HLLC 求解器对溃坝水流运动进行模拟;Zhou[18]建立了基于HLLC 求解器的二维水动力和水质耦合模型。对比HLL 求解器,HLLC 求解器可扩充浓度组分方程,为天然河道环境水力学数值模拟创造了有利条件,推广应用前景十分广阔。以往的研究中,多采用HLLC 求解器对浅水方程进行求解,而天然河道一维水动力通常以圣维南方程作为控制方程,采用HLLC 求解器对圣维南方程进行求解至今少见报道。与浅水方程相比,守恒型圣维南方程需考虑河宽及其沿程变化产生的影响,实际应用中,需重新推导基于守恒型圣维南方程的HLLC求解器中通量计算公式。
Godunov 格式下,为了获得高精度数值解,一般需要进行变量空间重构。以MUSCL[19](Monotonic Upstream-centered Scheme for Conservation Laws)为代表的变量空间重构方法应用比较广泛,但该方法仅适用于断面渐变条件下的变量空间重构。天然河道断面几何形状复杂,河宽和水深沿程快速变化,直接采用MUSCL法进行变量空间重构会产生较大误差。
本文采用守恒型圣维南方程作为天然河道一维非恒定流控制方程,基于Godunov格式,提出了天然河道断面几何形状快速变化条件下的变量空间重构方法,推导了基于守恒型圣维南方程的HLLC 求解器通量计算公式,为天然河道复杂水动力数值模拟提供一种高精度、简便的方法。
1 控制方程
守恒型圣维南方程组表达式如下[20]:
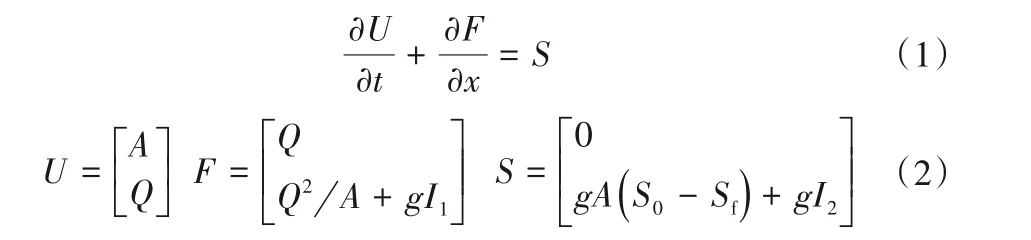
式中:U为变量;F为通量;S为源项;t为时间;x为空间坐标;A=A(x,t)为过流断面面积;Q为流量;g为重力加速度;S0为床面比降;Sf为摩阻比降;I1和I2分别为静力矩和侧压力,表达式如下:
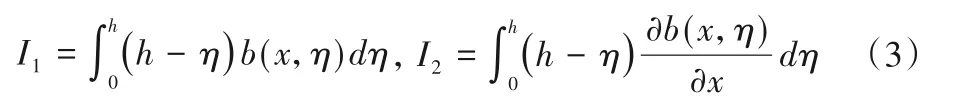
式中:h为水深;b(x,η)为断面宽度。
天然河道中,床面比降S0变化较大,在源项处理中通常避开底坡源项。Cunge[21]给出了对I1求导的表达式:
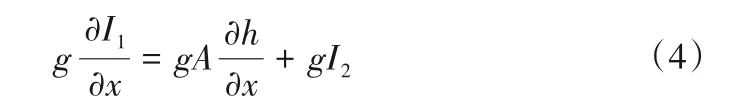
因此,式(2)中源项可改写为[22]:
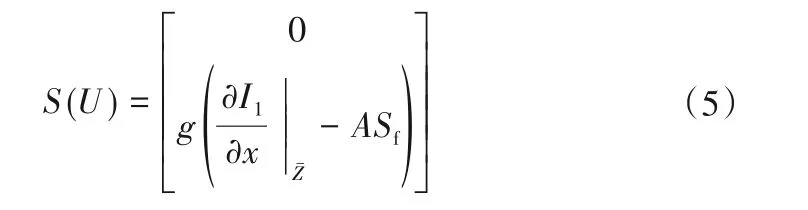
该源项处理方式是将侧压力项I2和床面比降S0转化为对静力矩I1的偏导,精度高且便于计算。
2 数值计算方法
2.1 离散方法
采用Godunov 格式的有限体积法对控制方程离散(见图1),表达式如下:

图1 中心格式有限体积法单元离散Fig.1 Finite volume element discretization with central scheme

式中:i为计算单元序号;n为时刻;Δxi为计算单元i的长度;Δt为计算时间步长,为n时刻最大波速;Fi+1/2和Fi-1/2分别为i+1/2和i-1/2界面处的通量。
2.2 HLLC近似Riemann求解器
HLLC近似Riemann求解器波的结构见图2。
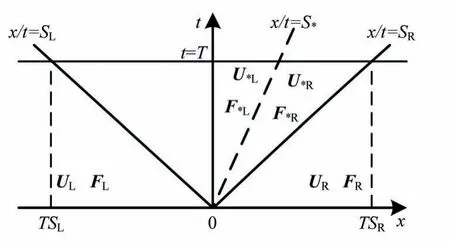
图2 HLLC近似Riemann求解器波结构Fig.2 Wave structure of HLLC approximate Riemann solver
HLLC 求解器是在HLL 求解器2 波族的基础上增加了中间波,中间波的波速为S*。HLLC通量表达式如下[9,16]:

式中:UL和UR分别为界面左侧和右侧变量;FL和FR分别为界面左侧和右侧通量;U*L和U*R分别为中间波左侧和右侧变量,为待求变量;F*L和F*R分别为中间波左侧和右侧通量;SL和SR分别为界面左侧和右侧波速。
在计算通量时,波速估计方法的选择至关重要,因为它们会影响数值结果的质量[23]。文献[9]建议采用如下方法估算波速:

式中:uL和uR分别为界面左侧和右侧流速;aL和aR分别为界面左侧和右侧重力波波速;qK(K=L,R)的表达式如下:
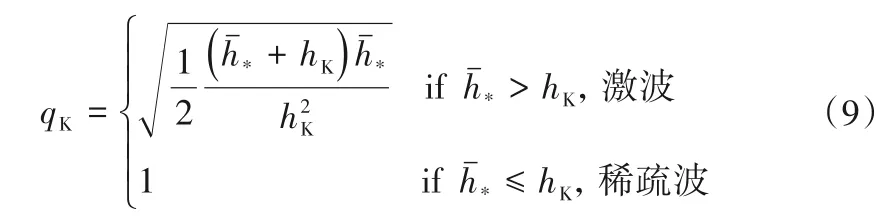
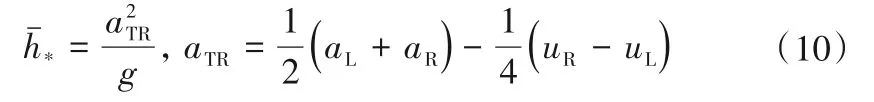
式中:aTR是基于界面左、右两侧均为稀疏波的假定对重力波波速a的估计值。
为了计算界面通量,还需U*L和U*R的值。这里引入如下假设[9,16]:
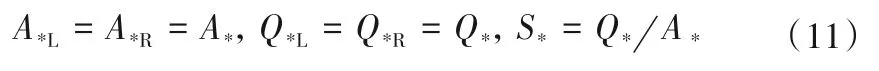
事实上,上述假设对于精确Riemann求解器也是正确的[16]。
本文推导得出基于守恒型圣维南方程的中间波变量U*=[A*,Q*]T以及中间波波速S*的表达式。
对跨越波速SL、SR和S*的状态分别运用Rankine-Hugoniot条件[24],可得:
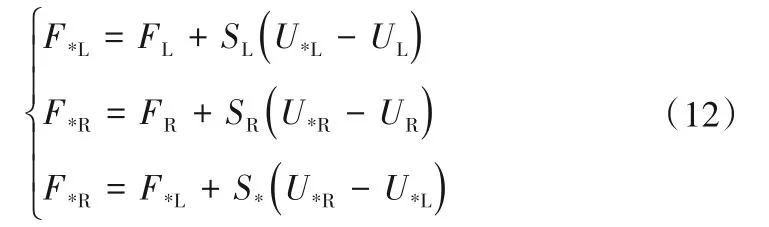
将式(2)中第一个分量(即质量守恒方程)带入式(12)中前两项,并将式(11)带入,可得:
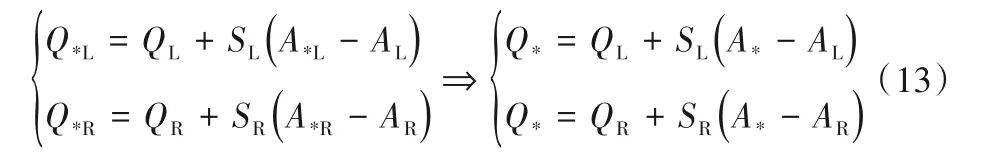
上式是关于Q*和A*的方程组,经求解可得:
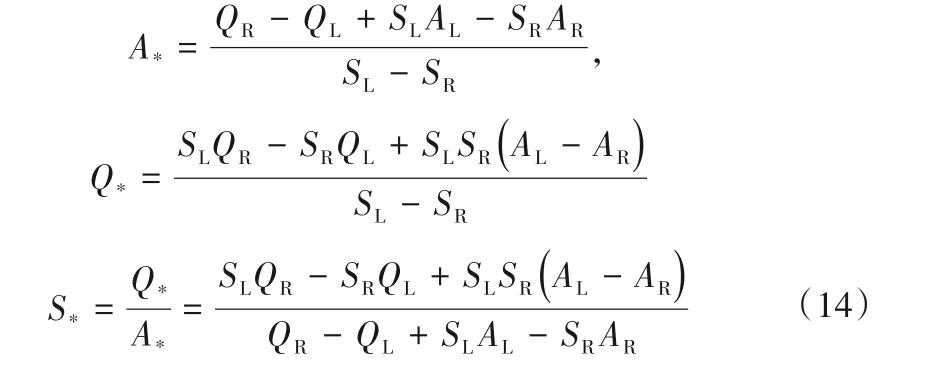
根据式(11)和式(12)的第三项可知,当HLLC 法应用于一维水动力方程数值求解时,U*L=U*R,并且F*L=F*R,通量计算表达式还可以写成:
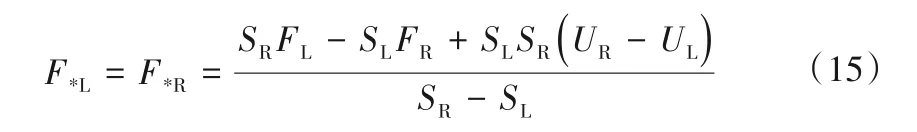
上式与HLL 通量计算表达式完全一致。由此可见,HLLC法引入的中间波仅作用于扩充的浓度组分方程,一维水动力计算中,HLLC法和HLL法计算结果完全一致。
2.3 变量空间重构
在变量空间重构中,MUSCL方法将单元平均值线性外推到单元界面,表达式如下:

为了避免虚假振荡,外推的斜率由斜率限制器函数限制。坡度限制器采用minmod 限制器,限制器中有2 个变量,当其符号相同时取其最小值,否则取0[25],因此单元坡度表达式如下:
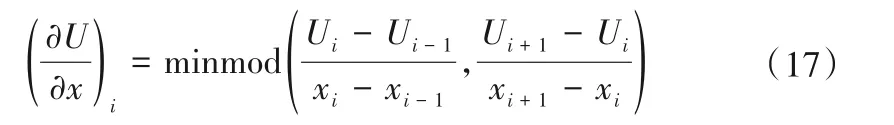
为了保证重构后的变量均为非负值,同时保证单元左右两侧重构值的平均值与单元平均值相等[26],表达式如下:
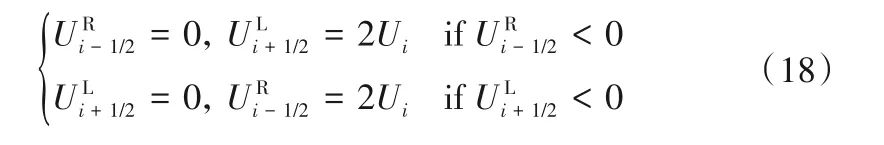
天然河道断面几何形状不规则,河宽和水深沿程快速变化,若直接按上述方法进行变量空间重构,可导致通量计算结果严重失真,无法保证格式守恒。本文首先依据过流断面面积和静力矩等效原则将河道断面概化成矩形,通过线性插值构造单元界面处断面几何形状,采用基于MUSCL法的水位空间二阶精度重构结果计算单元界面两侧过流断面面积和静力矩的重构值,保证计算格式守恒。具体步骤如下:
(1)天然河道断面概化方法。给定河道水位,首先计算过流断面面积A和静力矩I1(式(3)积分获得),依据过流断面面积和静力矩等效原则将天然河道断面概化成矩形,即:I1,其中分别为等效过流断面面积和等效静力矩。由此可推导出过流断面等效水深h′、等效河宽B′和等效河底高程,表达式如下:
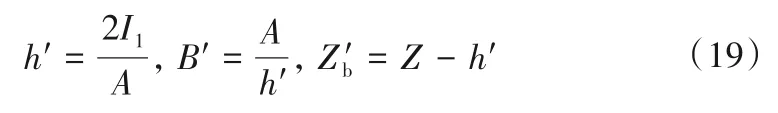
水深是波速计算的关键参数,天然河道通常采用h=A/B来计算断面平均水深,其中B为水面宽度。然而对于复式断面(见图3),B和h均存在突变(见图4),对变量空间重构产生明显影响。而等效水深和等效河宽则不存在突变。此概化方法保证单元水体受力条件不变,物理概念清晰,等效河宽和等效水深的概化结果唯一。
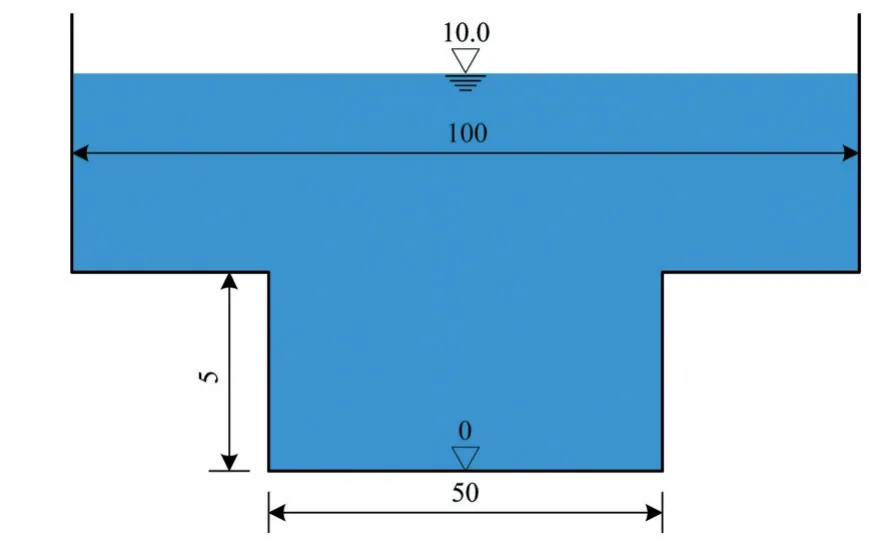
图3 复式断面示意图(单位:m)Fig.3 Schematic diagram of compound section

图4 断面平均水深和等效水深对比Fig.4 Comparison of section average water depth and equivalent water depth
(2)单元界面处断面几何形状构造。根据概化后相邻河道断面的宽度和底高程,通过线性插值构造单元界面处断面几何形状。以i+1/2界面处断面几何形状构造为例,表达式如下:

(3)变量空间重构。需空间重构的变量包括A、Q和I1。先采用式(16)构造界面处(以i+1/2 界面为例)的水位和流量,然后基于构造界面处过流断面面积和静力矩,表达式如下:

2.4 源项及边界条件
采用二阶龙格—库塔离散的时间分裂方法来处理源项[27]:
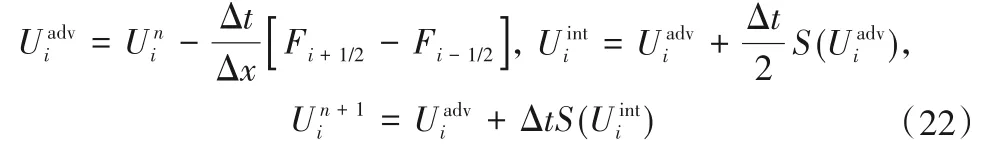
源项包括断面静力矩梯度和摩阻项。摩阻项可采用显格式处理,离散表达式如下:
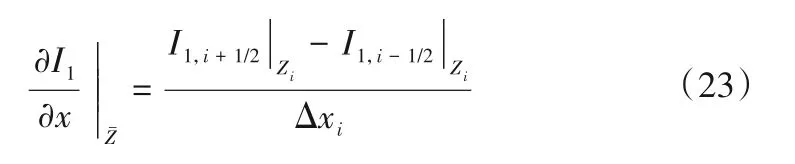
边界条件有两种:①固壁边界,引入反射边界条件,边界处的水位与邻近单元一致,而流速与邻近单元相反;②允许波穿过的边界条件,边界处的水位和流速与邻近单元一致。
3 算 例
3.1 天然河道洪水演进算例
某河流经盆地和峡谷,河道平面形态变化较大,常水位下河宽变化范围为200~1 000 m,河道平面示意图见图5,此河段长度59.44 km,布置实测大断面18条(0~17号)。
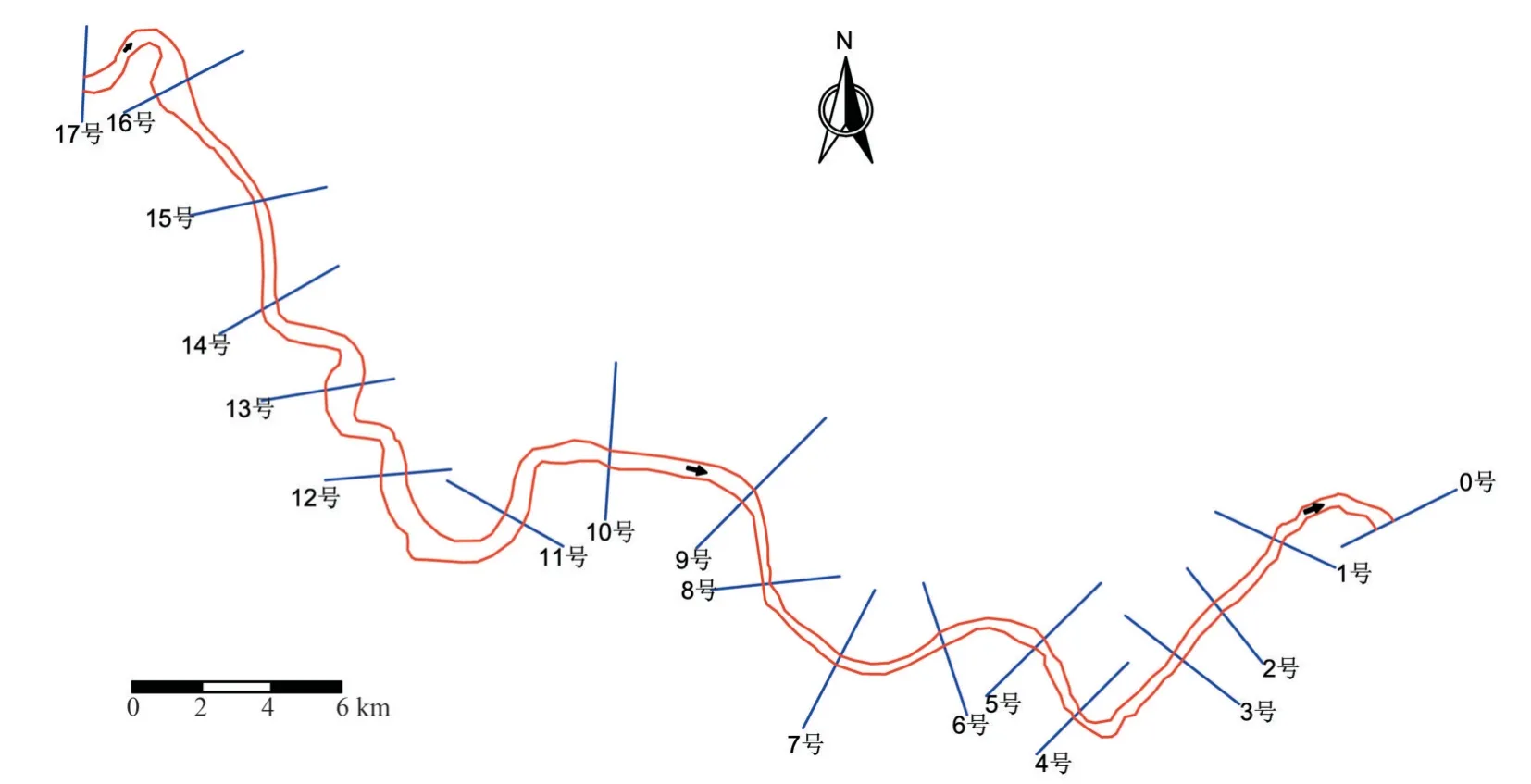
图5 河道平面示意图及断面布置Fig.5 Plan and section layout of river
河道典型横断面见图6。盆地河段为复式断面,河宽较宽,而峡谷段为“V”字形断面,河宽较小。河床纵断面起伏剧烈,深泓最低点高程-48.67 m,深泓最高点高程为33.3 m,纵断面见图7。该河段1994年发生了频率P=4%洪水,洪峰流量为44 400 m3/s(见图8)。洪水过后对各断面洪痕进行了准确测量,该场次洪水水面线数据完备、准确,可以此作为河道糙率率定以及计算结果验证的依据。根据洪痕实测数据,对洪峰流量条件下的河道糙率进行率定,糙率取值范围为0.028~0.088。

图7 河道纵断面图Fig.7 River profile

图8 1994年典型洪水过程Fig.8 Typical flood process in 1994
将断面计算最高水位与实测洪痕进行对比,结果见图9(本文方法简称“HLLC”)。为了便于对比,基于HEC-RAS 软件,采用相同的断面数据和边界条件,建立一维非恒定流数值计算模型,对1994年典型洪水过程进行计算(简称“HEC-RAS”);HEC-RAS[28]软件非恒定流控制方程为非守恒型,模型采用有限差分进行求解。文献[25]中非恒定流控制方程同为非守恒型,基于Godunov 格式,采用HLL 近似Riemann 求解器求解,采用该文方法同步进行对比(简称“HLL”)。
从图9 中可见,基于HLLC 算法的计算结果与实测值吻合良好,而HEC-RAS 和HLL法模拟结果与实测值有较大偏差,偏差的起始点位于9 号断面,9~8 号断面河道水面比降明显高于实测值,9 号断面上游水位计算结果均高于实测值,其中HECRAS 法偏差最大可达1.69 m(位于11 号断面),HLL 法偏差最大可达1.42 m(位于10号断面)。9~8号断面河道由盆地向峡谷过渡(见图6),河宽快速缩窄,断面最高水位对应的水面宽度分别为595 和269 m。以1994年典型洪水中最大洪峰起涨至消落过程为分析对象(6月16日-6月25日),将断面间动量方程对应的通量进行比较,守恒型方程的通量为Q2/A+gI1,非守恒型方程的通量为Q2/A,结果见图10。
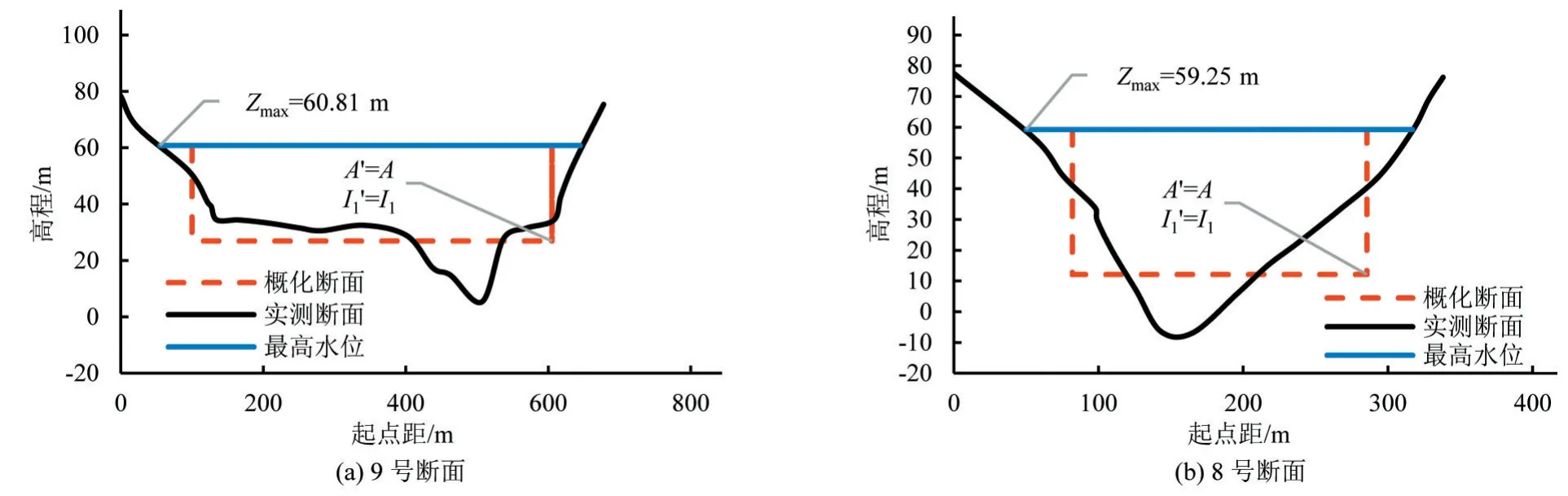
图6 河道典型实测断面及概化断面图Fig.6 Typical measured section and generalized section of river

图9 断面最高水位计算值与实测值对比Fig.9 Comparison of calculated and measured maximum water level
从图10 中可见,守恒型动量方程对应的通量,低水位情况下9 号断面小于8 号断面,而高水位情况下恰恰相反;非守恒型动量方程对应的通量,9 号断面在整个分析过程中均小于8 号断面。由式(6)可知,流量Q的大小取决于单元入口和出口通量差,以及源项大小。因断面间流量过程差异较小(见图11),在非守恒型动量方程下,单元入口通量明显小于出口通量,只能通过加大源项中的水面比降来提高河段流量,这也是HECRAS 和HLL 法计算出9 号~8 号断面河道水面比降明显偏大的根本原因,而本文HLLC 法采用守恒型方程则不会出现此偏差。由此可见,对于断面几何形状快速变化的河段,采用守恒型控制方程进行数值计算是十分必要的。
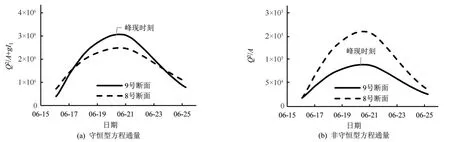
图10 断面间动量守恒方程对应通量比较Fig.10 Comparison of fluxes corresponding to momentum conservation equations between cross sections
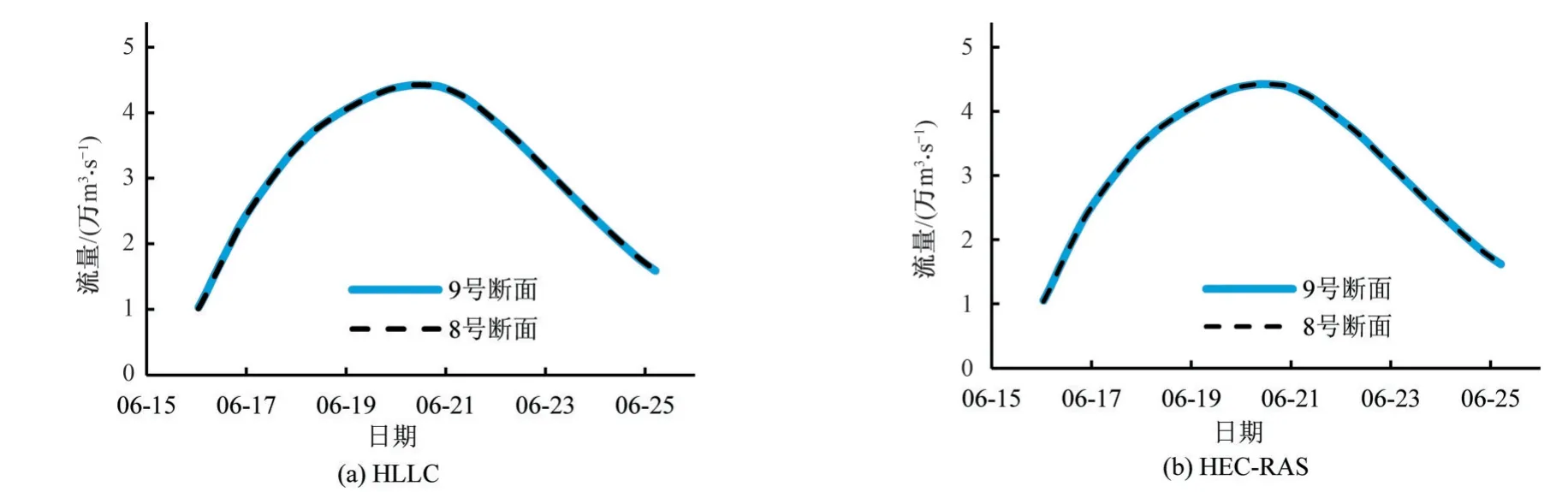
图11 流量计算结果Fig.11 Flow calculation results
天然河道断面几何形状快速变化,断面间水深和过流断面面积关系差别较大。以8号断面和9号断面为例(见图6),最高水位条件下8 号断面过流断面面积为9 595 m2,等效水深为47.13 m;而9 号断面过流断面面积为17 133 m2,为8 号断面的1.79 倍,等效水深为33.9 m,为8 号断面的0.72 倍。若直接进行变量空间重构则会产生较大误差,通量计算结果严重失真,同时也会产生格式不守恒问题。人为构造单元界面处断面几何形状,采用界面处基于MUSCL法的水位重构值计算与之对应的过流断面面积和静力矩,以此作为变量空间重构结果,成功避开了断面几何形状快速变化对变量空间重构的影响,同时保证了计算格式的守恒。
本算例HLLC法计算结果明显优于HLL法,主要原因为:①采用的控制方程不同,即守恒型圣维南方程优于非守恒型方程;②变量空间重构方法不同,即本文变量空间重构方法优于所有变量均直接采用MUSCL的变量空间重构方法。
3.2 喉口混合流算例
由于缺乏天然河道跨临界流的实测数据,本文采用喉口混合流这一经典算例检验模型模拟跨临界流以及浅水间断等复杂明渠水流运动的能力。明渠长度为3 m,渠宽、底高程均沿程变化,表达式如下:

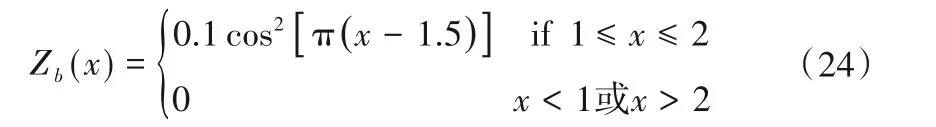
式中:B(x)为x处河宽;Zb(x)为x处河道底高程。

图12 河道底高程沿程变化Fig.12 Variation of river bottom elevation along the river
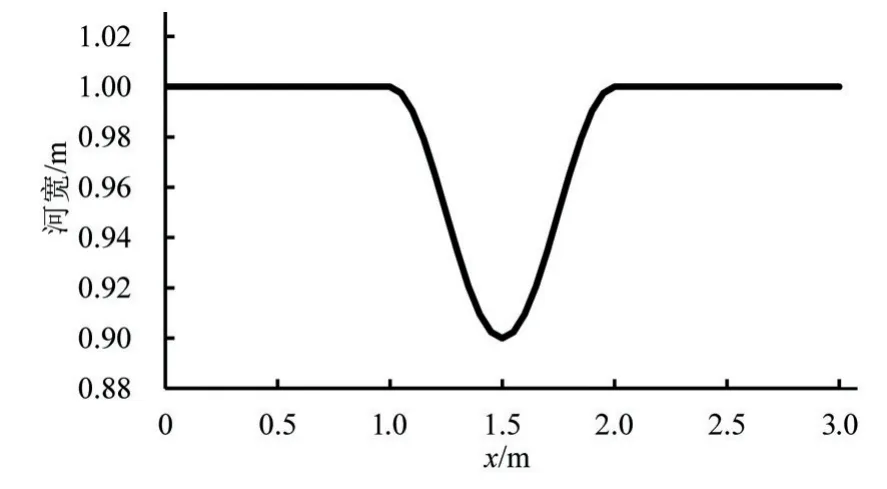
图13 河宽沿程变化Fig.13 River width variation along the river
渠道初始水位1.0 m,初始流量为0,入口流量Q=1.878 m3/s,下游水位Z=1.0 m。计算空间步长Δx为0.01 m,不计河道摩阻项。
计算结果表明(见图14),水位的计算值与解析解吻合较好:当0≤x≤1 时,水位计算值为1.094 1 m,而解析解为1.094 4 m;当x=1.92 m时,计算水位最低,其值为0.500 2 m,而解析解中当x=1.95 m 时,水位最低,其值为0.499 7 m。流量方面,计算值与解析解完全一致。

图14 混合流计算结果Fig.14 Calculation results of mixed flow
该算例中既有缓流又有急流,还存在跨临界流动,即水跌和水跃,是典型的浅水间断流动。本文算法对激波进行精确捕捉,计算精度高,适应性强。
4 结论
本文采用守恒型圣维南方程作为控制方程,基于Godunov格式,采用HLLC 近似Riemann 求解器对模型进行求解,主要结论如下。
(1)推导得出了基于守恒型圣维南方程的HLLC 近似Riemann 求解器通量计算表达式,将该求解器推广应用至天然河道一维非恒定流计算中。
(2)提出了针对天然河道复杂断面几何形状下的变量空间重构方法:提出了基于过流断面面积和静力矩等效原则的天然河道断面概化方法,通过线性插值构造单元界面处断面几何形状,基于水位的空间二阶精度重构结果计算界面两侧过流断面面积和静力矩的重构值,避免变量空间重构产生较大误差,同时保证计算格式守恒。
(3)天然河道断面几何形状快速变化条件下,本文方法计算结果与实测值吻合良好,明显优于HEC-RAS 法和HLL 法(非守恒型圣维南方程,MUSCL变量空间重构方法),同时对于混合水流运动以及浅水间断具有较高的模拟精度。
(4)本文将HLLC 近似Riemann 求解器由浅水方程拓展至守恒型圣维南方程,较HLL 求解器增加了中间波,可扩充浓度组分方程,为天然河道一维水动力及环境水力学高精度数值模拟提供了新的方法。□
