无上游来水城市河道径流分割及其下垫面影响

张金萍，王宇昊

（1.郑州大学水利科学与工程学院，郑州450001；2.郑州大学黄河生态保护与区域协调发展研究院，郑州450001）

0 引言

城市河道径流是城市水文过程的重要组成部分，也是城市用水和水资源管理的重要内容。与自然河道径流相比，城市河道径流水源组成更为复杂，采用适宜的方法对城市河道径流进行合理分割，不仅有助于对城市河道径流水源组成的科学认识，而且还将提升城市水文模拟精度与城市用水安全［1］。近年来，许多学者针对径流分割做出了相应的研究［2-4］，例如张泳华等采用数字滤波法和平滑最小值法对东江流域控制性水文站博罗站的实测日径流量进行径流分割，探究了降水和人类活动对基流的影响［5］；马晓婧等利用改进退水常数的数字滤波法对拒马河径流过程进行分割，分析了拒马河丰、平、枯年的基流变化特征［6］。这些研究中径流分割研究的对象主要是河川基流，而城市河道中存在大量的生活污水、工业废水，径流的成分发生了显著的改变，特别是对于上游天然来水被全部拦截，无上游来水的城市河道，更需要对其进行径流分割，从而进一步探究径流的组成部分及其演变过程。

下垫面是影响降雨-径流关系的重要因素［7，8］，伴随着城市化的发展，城市下垫面对径流的影响得到了广泛研究，例如李慧等运用水文特征参数时间序列法探究了西安市下垫面变化对城市河流灞河径流的影响［9］；赵彦军等利用SWMM 模型研究了下垫面城市化对济南小清河流域产汇流的影响［10］。然而城市河道尤其是无上游来水的城市河道，生活污水、工业废水的排放主要受人口、社会经济等条件的影响，导致总径流不能准确地反映城市真实的集水特性，因此通过径流分割得出的直接径流能更准确地反映下垫面对降雨-径流关系的影响。

本文以穿郑州市而过的贾鲁河为例，引入数字滤波法、滑动最小值法和时间步长法，对郑州市中牟水文站2003-2016年的逐日径流进行径流分割，筛选出最优分割方法后，采用年直接径流系数表征郑州市区的集水特性，结合郑州市区5 期土地利用/覆盖数据，构建年直接径流系数和各类下垫面面积的多元回归模型，并对2017年和2018年的年直接径流系数进行预测，从而更准确地反映下垫面城市化对降雨-径流关系的影响。

1 数据与方法

1.1 研究区域概况

贾鲁河属淮河水系，是淮河支流沙颍河的支流，发源于新密市（隶属郑州市），向东北流经郑州市区，至市区北郊折向东流，流经中牟、开封后，在周口市入沙颍河，最后流入淮河。贾鲁河全长246 km，流域面积5 896 km2，主要支流有金水河、索须河、熊儿河、七里河、东风渠等［11］。

本文研究区域为贾鲁河流域郑州市区段，郑州市区境内贾鲁河长68 km，流域面积993 km2，约占郑州市区总面积的94%。由于贾鲁河上游存在常庄水库，尖岗水库，河王水库等水利枢纽，因此除贾鲁河主河道外，其他支流均属小河渠，基本无天然水源，已经成为城市排污、农灌退水及泄洪排水的渠道。此外，郑州市区雨水的排放，主要是就近排入河道，市区内的雨水分别从贾鲁河、东风渠、金水河、熊儿河、七里河等泄洪河道汇入贾鲁河后，排出市外［12］，河流水系图见图1。日径流数据来源于中牟水文站实测资料，市区年降雨数据来源于郑州市水资源公报。

图1 郑州市区贾鲁河水系Fig.1 Drainage map of the Jialu River in urban area of Zhengzhou

1.2 数字滤波法

数字滤波法的基本原理是将流量过程转化为数字信号，通过数字滤波器将信号分解为高频和低频，对应地将径流过程划分为地表径流和基流［13］。目前应用广泛的数字滤波法有：Lyne-Hollick 滤波法（F1）、Chapman 滤波法（F2）、Chapman-Maxwell 滤波（F3）和Boughton-Chapman滤波法（F4）。

F1法的径流分割方程为：

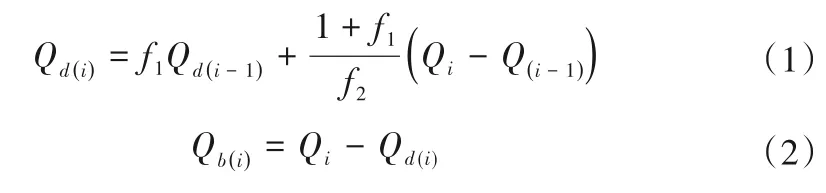
式中：Qi为第i时刻的径流量；Qd（i）为第i时刻的地表径流量；Qb（i）为第i时刻的基流量；f1为滤波系数，一般取0.8～1.0；f2一般取0.5［14］。

由F1法改进的F2法基流分割方程［15］为：

F3法的基流分割方程为：

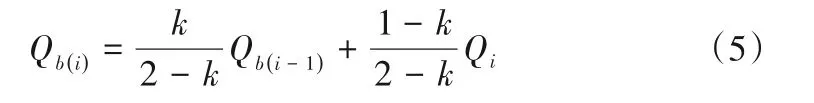
式中：k为退水系数，一般取0.95［16］。

F4法的基流分割方程［16］为：

式中：参数C一般取0.15［17］。

1.3 滑动最小值法

滑动最小值法是一种径流快速分割方法，基本原理是通过确定时间步长N将逐年的日径流过程分成若干个时间段，若某一时间段的最小流量值与拐点检验因子f的乘积小于等于相邻时间段的最小流量值，则该时段的最小流量值即为流量过程线上的一个拐点。重复以上步骤，确定所有拐点后进行连接得到基流过程线。滑动最小值法目前主要有标准BFI（f）法和改进BFI（k）法两种，相应的拐点检验因子f和k分别取0.9 和0.979 15［18］。

1.4 时间步长法

时间步长法又称为HYSEP 法，包括固定时间间隔法（FI）、滑动时间间隔法（SI）和局部最小值法（LM）等3 种流量分割方法［19］。运用该方法进行径流分割，首先要计算的是直接径流所持续的时间，目前计算该时间采用的是经验公式：

式中：T为直接径流持续天数，d；A为流域面积，km2。

确定直接径流持续天数后，取与2T最为接近且介于3～11 d的奇数作为分割的时间间隔参数N进行流量分割［20］。

1.5 多元线性回归模型

多元线性回归模型的核心在于建立因变量和两个或两个以上自变量之间的线性关系，模型建立前，需要分析各自变量对因变量影响的显著性并选择对因变量影响较大的自变量，从而合理构建模型。假设因变量为y，自变量为x1、x2、…、xn，则多元线性回归模型如下：

式中：β0为模型的常数项；β1～βn为偏回归系数；ε为去除自变量对因变量影响后的随机误差。常数项和偏回归系数的值可根据最小二乘法确定［21］。

2 流量过程线的自动分割

2.1 径流分割的可行性论证

进入21世纪以来，郑州市城市化程度不断提高，伴随着人口城市化和下垫面城市化程度的提高，城市河道的径流量和径流成分发生了较大的变化。根据中牟水文站2003-2016年逐日径流资料，计算168 个月的月径流量和逐月最小日径流量见图2。

图2 中牟水文站逐月降水量-月径流量-月最小日径流量Fig.2 Monthly precipitation-monthly runoff-monthly minimum daily runoff of Zhongmu hydrological station

由图2 可得非汛期（10-4月）的月径流量和月最小日径流量均呈现一定的增长趋势，径流的年内变化进一步减小。结合实际情况，随着地下水位下降，贾鲁河及其支流的地下水已经少之又少，加上上游尖岗、常庄等水库的截留，导致贾鲁河基流严重匮乏［22］；另一方面，伴随着人口的增长和社会经济的发展，市区排放的生活污水和工业废水显著增长，而这一部分废污水排放在贾鲁河径流中占据了较大的比例。

在拟采用的3 种流量过程线自动分割方法中，数字滤波法实质上是将快速响应的直接径流视为高频信号，将慢速响应的地下径流视为低频信号，从而进行流量分割，而市区排放的生活污水和工业废水等径流成分在年内较为稳定，可以视为低频信号；滑动最小值法实质上是由总径流曲线上的一系列转折点所形成的折线，从而实现对流量的自动分割；时间步长法则是根据直接径流的持续天数进行流量分割。因此，这3 种自动流量分割方法在无天然来水的城市河道中均具有一定的适用性，可以将贾鲁河的径流划分为直接径流和基流，其中直接径流指的是当地降雨形成的地表径流量，而基流则包括生活污水和工业废水等。

许多研究表明：对于F1，当滤波次数N取3 即正向-反向-正向滤波，且滤波参数f1控制在0.90～0.95 间能够得到较好的分割结果，同时增大滤波参数减少次数可以得到相同的结果［23-24］，在此基础上，f1分别取0.9，0.925，0.95进行流量分割；对于F2，F3和F4 法均选择默认的参数；对于滑动最小值法，由于研究区域面积较小，时间步长N分别取3，4，5；对于时间步长法，根据流域面积计算得时间间隔参数N=9。

2.2 径流分割结果分析

通过上述3 类9 种方法对实测日径流量进行径流分割，分割后的结果用年基流指数BFI表示（图3），其中BFI为当年基流量和总径流量的比值。

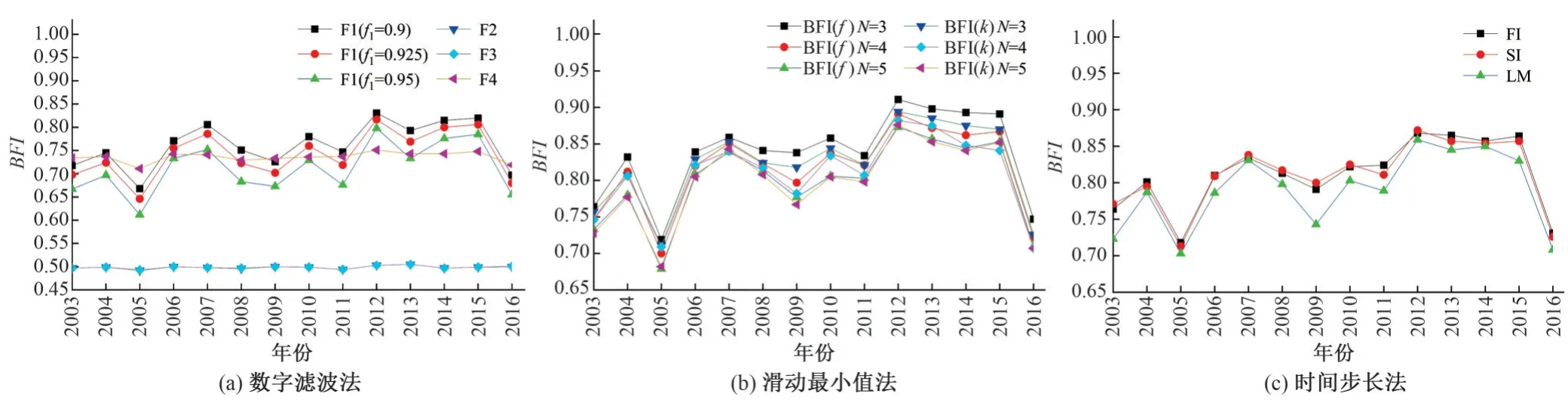
图3 径流分割结果Fig.3 The results of runoff division

由图3 可得：数字滤波法中，F1 法的参数f1越大，BFI值越小；F2 和F3 法对应的BFI基本一致且显著偏小，在年际间波动很小；F4 的分割结果与F1 相近，但又存在一定差异，且相应的BFI值在年际间波动较小；滑动最小值法中，无论是标准BFI（f）法还是改进BFI（k）法，N值越大，BFI越小；时间步长法中，FI和SI的分割结果基本一致，而LM法对应的BFI值小于二者。

为了更直观地了解日基流量分割情况，选择2011年为典型丰水年，2008年为典型平水年，2012年为典型枯水年，对汛期（5月至9月）日径流的分割结果分别见图4-6。

图4 2011年汛期基流过程线Fig.4 Base flow process line in flood season of 2011

图5 2008年汛期基流过程线Fig.5 Base flow process line in flood season of 2008

由图4、5 和图6 可得，不同分割方法所得的基流过程线差异较大。无论是丰水年、平水年还是枯水年，数字滤波法中，F1法的基流过程线波动较小且随洪峰变化不大；F2 法和F3 法的基流过程线基本重合，与F4的波动趋势基本一致，但F4的基流过程线显著高于F2 和F3，且随着洪峰变化有明显反映；滑动最小值法中，当N相同时，标准BFI（f）法和改进BFI（k）法的基流过程线基本一致，且两种方法的基流过程线均有明显的起伏波动，会出现基流量等于径流量的情况。时间步长法中，FI 和SI法的基流过程线呈现明显的阶梯型波动，有较多的明显拐点，不符合无上游来水的城市河道中的基流产生机理；LM 法的基流过程线较FI和SI略为平缓，基流变化趋势随着径流过程变化趋势变化，且滞后于洪峰过程。

图6 2012年汛期基流过程线Fig.6 Base flow process line in flood season of 2012

2.3 最优分割方法的确定

枯水指数（Q90/Q50）是反映地下水补给河川径流特性的重要指标，其中Q90和Q50分别代表时段内出现频率大于等于90%和50%时的径流量，即枯水指数在一定程度上可以代表河道中常年存在的径流量占总径流量的比例［25］，因此本文径流分割的合理性可以用枯水指数来衡量。

将枯水指数与年总径流量的乘积视为河道中常年存在的径流量，用于和分割出的年基流量进行对比，将决定系数R2、纳什效率系数NSE和平均相对误差Re作为评价标准，验证结果见表1。评价标准的公式如下：

式中：Qk为第k年观测的年基流量；Sk为第k年估算的年基流量；为观测的年基流量均值；为估算的年基流量均值；n为样本个数。

由表1 得：F2 和F3 法估算的年基流量值偏小，NSE为负数且Re高达34%，说明这2 种方法在本研究区域的年基流量估算中不理想；FI 和SI 法的NSE介于0.7 和0.8 之间，但Re均超过10%，说明这两种方法在本研究区域的年基流估算中效果一般，具有一定的模拟效果；同理，无论是BFI（f）还是BFI（k），N=5 时的基流估算效果最好，N=3 或4 时效果一般。F1、F4、BFI（N=5）、LM 法的NSE均超过了0.8，且Re控制在10%以下，说明这些方法对基流的模拟效果很好。其中，F1 法（f1=0.925）的NSE最高且Re最小，估算的基流量与实际观测值的模拟效果最好，结合2.2中对典型年内的基流过程线分析，选择F1法（f1=0.925/N=3）的分割结果作为实际的径流组成。

表1 各径流分割方法的验证结果Tab.1 Verification of runoff division methods

3 下垫面对直接径流的影响

3.1 径流分割成果

根据F1 法（f=0.925/N=3）分割的成果，得到中牟水文站2003-2016年径流分割结果见图7。

图7 2003-2016年径流量-年基流量-年直接径流量Fig.7 Annual runoff-annual base flow-annual direct flow from 2003 to 2016

由图7可得郑州市贾鲁河年径流量和年基流量的变化趋势基本一致，且年基流量显著大于年直接径流量，因此贾鲁河年径流量增大的主要原因是伴随着郑州市人口的增长和社会经济的发展，市区的生活污水、工业废水等排放量增大，这一部分径流对总径流增长的贡献率为83.96%，而年直接径流对总径流增长的贡献率为16.04%，年直接径流量和市区年降雨量的变化见图8。

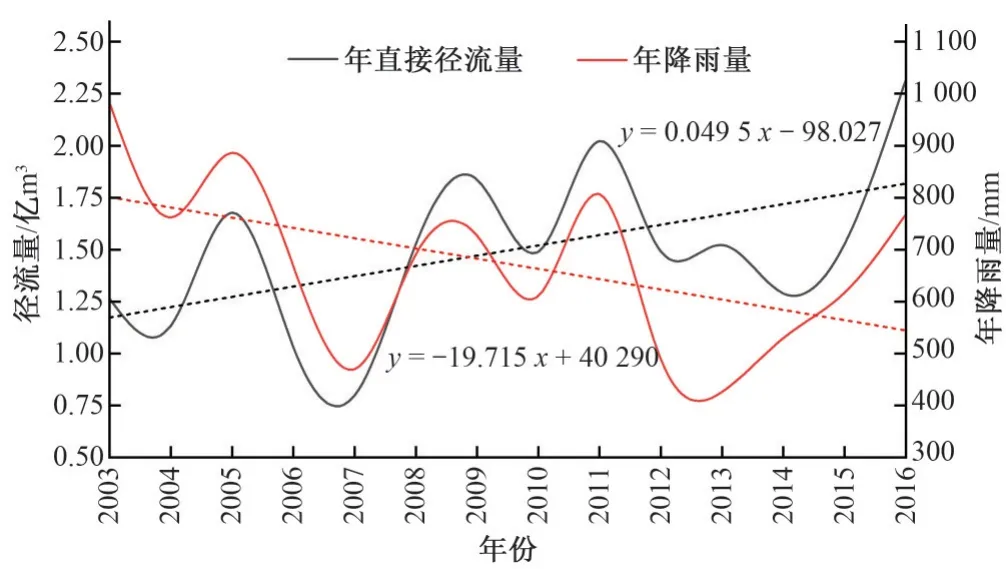
图8 2003-2016年直接径流量和年降雨量变化Fig.8 The change of annual direct runoff and annual rainfall from 2003 to 2016

由图8 可得，2003-2016年降雨量整体上呈减少趋势，而年直接径流量呈增长趋势，且同一年降水量级下的年径流量显著增大，其中2013年降雨量最小，但年直接径流量大于2012 和2014年直接径流量，这是由于2013年贾鲁河单位生态补水量为10.16 m3/s，显著大于其他年份，因此在径流分割中一部分生态补水量被计入了直接径流中，在对该年径流分割结果进行相应的调整后计算多年直接径流系数见图9，其中年直接径流系数为年直接径流深与年降雨量的比值，年直接径流深由年直接径流量和流域面积计算所得。

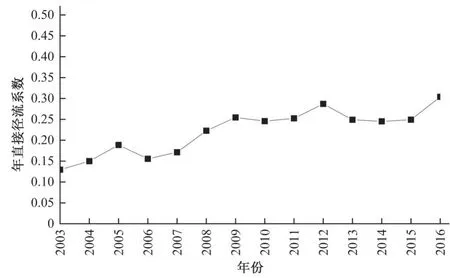
图9 2003-2016年直接径流系数Fig.9 Annual direct runoff coefficient from 2003 to 2016

3.2 城市下垫面变化分析

根据2000，2005，2010，2015，2018年五期精度为30 m 的郑州市区土地利用数据（图10），将其重分类为六类：耕地、林地、草地、城乡工矿居民用地、水域和未利用地，并分别计算各时期郑州市区的耕地、林草地，城乡工矿居民用地和水域的面积见表2。

图10 郑州市区2000，2005，2010，2015，2018年土地利用/覆盖分类Fig.10 Land use/cover classification of Zhengzhou City in 2000，2005，2010，2015 and 2018

结合图10和表2可得2000-2018年郑州市区的耕地面积持续减少，城乡工矿居民用地面积持续增长，二者的变化量基本相等，即减少的耕地大多转化成了不透水地面，且二者在2005-2010 这一时段内变化最为显著，在2010-2015 这一时段内变化不大；林草地面积在2005-2010年显著减少，在其他时段变化不大；水域面积在2000-2015年持续增加，但变化不大，在2015-2018年呈显著减少趋势。

表2 不同时期各类土地利用/覆盖面积 km2Tab.2 Area of different land use/cover in different periods

假设2000-2005，2005-2010，2010-2015，2015-2018 等时段内各类土地利用面积呈线性均匀变化，生成2003-2016年各类土地利用面积的时间序列，结合年直接径流系数序列作相关分析见表3。

由表3 可得：2003-2016年，城乡工矿居民用地面积和年直接径流系数的相关性最好且呈正相关，这是由于随着市区不透水面积的增大，下渗水量减小，从而导致降雨产生的直接径流量增大；耕地面积、林草地面积和年直接径流系数相关性较好且呈负相关；水域面积和年直接系数呈正相关且相关性较差，这与水域面积和径流量呈负相关的实际情况不符，主要原因是水域面积变化较小，它对年直接径流系数的真实影响被其他下垫面的变化所掩盖。

表3 年直接径流系数和各类下垫面面积的相关系数Tab.3 The correlation coefficient between annual direct runoff coefficient and various underlying surface areas

3.3 多元线性回归模型构建

由于研究区域面积一定且未利用地面积可忽略不计，因此城乡工矿居民用地、林草地、水域、耕地等4 类土地利用的面积之和大致为一定值，即4个变量间存在确定的线性关系，因此为避免自变量出现显著的共线性关系，在进行多元回归分析时，至多选取3个变量作为自变量。由于减少的耕地面积基本上全部转变为城乡工矿居民用地，因此选取城乡工矿居民用地面积（S1）、林草地面积（S2）、水域面积（S3）作为自变量，年直接径流系数为因变量y，根据最小二乘法构建多元回归模型为：

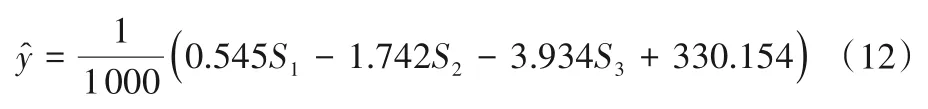
利用线性关系的显著检验方法（F检验法）对该模型进行检验，计算得F=27.261，大于在0.01 水平上的临界值6.552，即该模型在0.01水平上显著。模型模拟结果见图11。

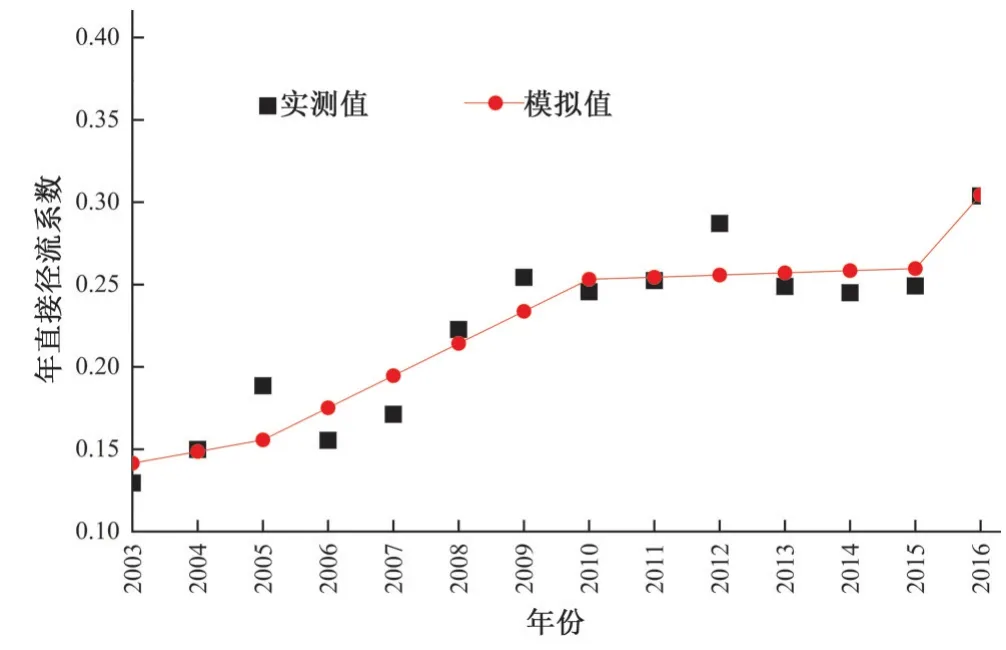
图11 年直接径流系数实测值和模拟值Fig.11 Measured and simulated annual direct runoff coefficient

由图11 可得：模型模拟值与实测值相比，纳什效率系数NSE、决定系数R2、平均相对误差Re分别为0.891，0.891 和6.72%，且各年年直接径流系数的相对误差均小于20%。将2017年和2018年的城乡工矿居民用地面积、林草地面积、水域面积输入该多元线性回归模型，预测这两年的年直接径流系数分别为0.349 和0.394。

利用数字滤波F1 法（f1=0.925/N=3）对中牟水文站2017年和2018年的逐日径流量进行分割，可得年直接径流量分别为1.695亿m3和2.114亿m3，结合年降水量计算年直接径流系数分别为0.333 和0.359。该多元线性回归模型对2017、2018年直接径流系数预测的相对误差分别为4.80%和9.75%，因此该多元线性回归模型具有良好的模拟效果，在一定程度上量化了下垫面对年直接径流的影响，更加清晰地反映了郑州市区下垫面城市化对降雨-径流关系的影响。

4 结论

将不同的径流分割方法应用于贾鲁河这一无上游来水的城市河道，分析典型年内的基流过程线，并将枯水指数作为衡量分割合理性的标准，从而确定最优分割方法，结果表明：数字滤波F1 法（f1=0.925/N=3）在贾鲁河的径流分割效果最好，有效地将径流分割为直接径流和基流；2003-2016年，基流和直接径流对年总径流增长的贡献率分别为83.96%和16.04%。

基于径流分割成果，利用年直接径流系数表征郑州市区的集水特性，结合5 期土地利用数据构建2003-2016年直接径流系数和各类下垫面面积的多元线性回归模型，并对2017年和2018年的年直接径流系数进行预测，得出以下结论：年直接径流系数总体上呈增长趋势，且与城乡工矿居民用地的面积显著正相关；该多元回归模型在0.01 水平上显著，且具有良好的模拟效果，NSE、R2和Re分别为0.891，0.891 和6.72%。此外，该模型对2017、2018年直接径流系数预测的相对误差分别为4.80%和9.75%。

对于无上游来水的城市河道，利用流量过程线的自动分割方法从总径流中分割出直接径流，剔除与产汇流无关的生活污水、工业废水等径流成分，能更清晰地反映下垫面对降雨径流关系的影响，对流域水资源的规划与管理具有重要的理论与现实意义。□