基于TVF-EMD与LSTM神经网络耦合的月径流预测研究
2022-02-23王文川
王文川,高 畅,徐 雷
(华北水利水电大学水资源学院,郑州450046)
径流变化受多种因素的影响,主要包括气候变化、人类活动、土地利用变化和植被覆盖等[1]。正是由于这些不确定因素的影响,径流序列呈现出非平稳性和多频性的特征,为相关部门进行径流预测带来了难度[2]。目前,学者们已经提出许多方法用于径流预测,其中“分解—预测—重构”[3]模式的预测模型被广泛应用,相比于传统模型它能有效提高预测精度,为水文预测提供了一种新思路。该模式的预测模型首先将非线性非平稳的径流序列用分解方法进行平稳化处理,并结合水文模型构成耦合模型进行预测。如Feng 等[4]将变分模态分解与基于粒子群优化的支持向量机模型结合,对长江流域的三峡水库和丹江口水库进行月径流预测,取得了较好的效果;李继清等[5]将极点对称模态分解与BP 神经网络组合,对黄河上游的唐乃亥站进行中长期径流预测,有效提高了径流的预测精度;梁浩等[6]提出了将经验模态分解和集合经验模态分解分别与不同模型结合,构建多种混合模型,对水文序列进行径流预测研究;席东洁等[7]将EMD(Empirical Mode Decomposition)与Elman 神经网络模型构成月径流预测模型,并验证了模型的可行性。这些研究表明,“分解—预测—重构”模式的模型在径流预测方面的应用能取得较好的效果,它既方便计算,又具有较高的精度,被广泛认可。该模式中“分解”阶段采用的方法有经验模态分解(EMD)、集合经验模态分解(Ensemble Empirical Mode Decompo⁃sition,EEMD)、变分模态分解(Variational Mode Decomposition,VMD)等,这些方法进行分解后,分量存在噪声和模态混叠等问题,对模型精度有较大的影响。EMD[8-9]广泛应用于非线性非平稳序列的分解中,但该种方法由于其严格的分频条件,使分量中存在模态混叠问题,并不具有较高的频率分离性能;EEMD[10,11]在EMD 的基础上有了提高,但在分解过程中添加的白噪声会导致重构误差,使得分解后低频序列同样存在模态混叠问题;VMD[12]、CEEMD(Complete Ensemble Empirical Mode Decomposition)[13]和CEEMDAN(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise)[14]对噪声具有稳健性,但这三种方法需对参数适当选择,且由于它们的截止频率是恒定的,使得序列不具有时变性。综上分析可得,现采用的模态分解方法存在①模态混叠;②不具有时变特性;③低采样率下性能差等问题,在一定程度上会影响模型预测精度。本文采用时变滤波(Time Variable Filter,TVF)经验模态分解(TVF-EMD)利用非均匀B 样条逼近作为时变滤波器,自适应地设计了局部截止频率,在解决模态混叠问题的同时保留了序列的时变性。并且在低采样率下设置了带宽阈值,使得序列在低采样率下也具有较好的性能。因此,TVF-EMD 方法更适用于非平稳序列的径流预测。本文将TVF-EMD 方法与长短期记忆神经网络(Long short-term memory,LSTM)耦合,提出了TVF-EMD-LSTM神经网络耦合的月径流预测模型,并在洛河流域长水水文站的月径流预测中验证了其效果,结果表明提出的耦合模型能有效提高月径流预测的精度,为当前径流预测提供了一种新的途径。
1 研究方法
1.1 TVF-EMD基本原理
TVF-EMD 方法2017年由Li 等[15]人提出,该方法是对EMD方法的改进和提高。TVF-EMD 方法采用时变滤波器来解决模态混叠问题,以保持序列的时变性。该方法充分利用瞬时幅值和瞬时频率,自适应的设计了局部截止频率,对给定序列进行时变滤波,并将其分为局部高频分量和局部低频分量,以得到固有模态函数(Intrinsic Mode Function,IMFs)。
TVF-EMD方法的计算步骤为:
(1)利用Hilbert 变换计算径流序列X(t)的瞬时幅值A(t)和瞬时频率φ’(t);

(2)确定瞬时幅值A(t)的局部极大值序列和局部极小值序列,分别表示为A({tmax})和A({tmin});
(3)对A({tmax})进行插值得到β1(t),以同样的方法对A({tmin})进行插值得到β2(t),计算瞬时均值a1(t)和瞬时包络a2(t):

(4)分别对A2({tmin})φ′({tmin})和A2({tmax})φ′({tmax})进行插值,得到η1(t)和η2(t)并计算瞬时频率分量φ′1(t)和φ′2(t):

(5)计算局部截止频率φ′bis(t):
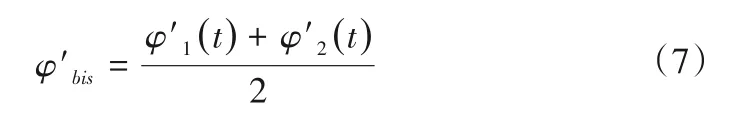
(6)为解决间歇问题,重新对局部截止频率φ′bis进行调整;
(8)计算停止准则θ(t),如果θ(t)≤ξ,则可确定X(t)为一个IMF,不满足则令x1(t)=xt-m(t),重复执行(1)~(8)步骤:

式中:BLoughlin(t)为两分量信号的Loughlin 瞬时带宽;φavg(t)为单个分量瞬时频率的加权平均值;m(t)为瞬时包络局部平均值。
分解后得到的所有模态分量Xi(t)之和为原径流序列X(t)的值。
1.2 LSTM神经网络模型
Hochreiter 等[16]人提出的长短期记忆神经网络(LSTM),解决了循环神经网络(Recurrent Neural Network,RNN)存在的长期依赖问题,较好地避免了梯度爆炸问题,是一种特殊的循环神经网络。LSTM 的基本结构如图1所示,包括输入层、循环层和输出层,其中Xt为输入序列,Yt为输出序列。相比于其他神经网络模型,LSTM 模型增加了“门”的结构,包括遗忘门、输入门和输出门。这些“门”用来控制记忆单元中的原信息的保存、丢弃,以及新信息的保存,使得LSTM 神经网络可以学习跨度相对较长的依赖关系,且不会出现梯度消失和梯度爆炸的问题[17]。

图1 LSTM基本结构Fig.1 Basic structure of LSTM
1.3 模型构建
由于径流序列的多频性和非平稳性,采用单一LSTM 神经网络模型预测精度不高,因此,本文提出先采用TVF-EMD 方法对径流序列进行平稳化处理,再用LSTM 神经网络模型对经过平稳化处理的子序列进行预测,最终将每个子序列的预测结果叠加重构,构成耦合的TVF-EMD-LSTM 预测模型。为了验证TVF-EMD-LSTM 耦合模型的有效性,分别与EMD-LSTM 模型和CEEMDAN-LSTM 模型进行对比,各耦合模型结构图如图2所示,计算步骤如下:

图2 各耦合模型结构图Fig.2 Structure diagram of each coupling model
(1)对洛河流域长水水文站的月径流序列X(t)进行TVFEMD、EMD 和CEEMDAN 分解,分别得到不同时间尺度下的固有模态函数(IMFs);
(2)设置模型参数,采用自相关系数(ACF)和偏自相关系数(PACF)研究前期流量对当前流量的影响,以确定各模型输入序列(IMFs)滞时;
(3)将分解后的IMFs 分别输入LSTM 神经网络模型中,选取每个子序列的90%用于训练,10%用于预测,对训练和预测序列分别进行归一化处理,进行正向迭代计算;
(4)当模型达到最大迭代次数后,停止迭代,分别输出IMFs训练序列和预测序列;
(5)将IMFs 训练和预测输出序列分别加和重构,则Y为最终的预测径流序列。
在输入数据前,需先确定LSTM 神经网络模型的参数以及输入模型变量个数。为了比较,所采用的耦合模型与LSTM 模型参数设置相同。根据Ding 等[18]的研究设置隐含层为200 层,迭代次数为500次时模型具有较好的性能。学习率过大导致不收敛,过小导致收敛速度慢迭代次数增多[19],经测试采用0.01的学习率可获得较高的精度。由于LSTM 模型是以数据驱动的预测模型,输入不相关的变量对模型预测结果有较大的影响,因此选择适当的滞时变量个数尤为重要。Sudheer 等[20]建议通过不同滞时下的相关性计算以及考虑流域实际情况,进一步分析前期流量对当前流量的影响以确定输入序列滞时。
1.4 模型评价标准
为了能更加直观地体现各模型预测结果的可靠性和精确性,选取均方根误差(RMSE)、确定性系数(DC)、平均绝对百分比误差(MAPE)、平均绝对误差(MAE)和预测精度等级五项指标作为模型评价标准。根据规范,当DC≥0.90时,预测精度为甲级,0.70≤DC<0.90 时,预测精度为乙级,0.50≤DC<0.70 时,预测精度为丙级。计算公式如下:

式中:Q0(i)为实测径流量值;Qc(i)为预测径流量值,万m3。
2 实例应用
洛河流域是黄河右岸的重要支流,流域总面积18 881 km2。其发源于陕西省商洛市洛南县洛源镇的龙潭泉,横穿洛南县中南部,最后由巩义东北注入黄河[21]。河道全长477 km,陕西境内河长129.8 km,河南境内河长366 km,多年平均径流总量达6.65 亿m3。月径流数据来源于河南省洛河流域的长水水文站,该水文站位于故县水库下游,是国家基本水文站。其流域示意图如图3所示。

图3 洛河流域示意图Fig.3 Schematic diagram of Luohe River Basin
2.1 TVF-EMD分解
选取长水水文站1987-2016年实测月径流数据,对径流序列进行Daniel 平稳性检验,由假设检验计算得出统计量|T|=145.847 7>t0=1.966 6,则可判断该序列为非平稳性序列,对预测结果有较大的影响。选用能自适应序列特征的TVF-EMD 方法进行分解,经调试当设置参数带宽阈值为0.3,B-样条阶次为26 时,TVF-EMD 具有鲁棒性。其分解结果如图4所示,由图4可以看出,TVF-EMD 方法将月径流序列分解为9 个IMFs,依次由高频到低频排列。IMF1 的频率最高、波长最短,序列最不稳定,随着分解模态数量的增加,模态分量的振幅逐渐减小,波长增加,序列逐渐趋于稳定。原径流序列振幅变化极不规律,序列稳定性较差,因TVF-EMD 分解能够自适应序列的特征,分解并不要求上下包络对称,通过分解后,各IMFs的波动性降低,且具有一定的周期性。综上所述,TVF-EMD 进行了有效的分解,具有较高的信噪比,且在保持径流序列时变性的前提下解决了模态混叠问题和噪声问题,是一种有效的序列分解方法。为验证该分解方法的优化效果,将该径流序列分别用EMD 和CEEMDAN 进行分解,EMD 分解后得到8 个IMFs,CEEMDAN 分解后得到9个IMFs。

图4 月径流序列TVF-EMD分解图Fig.4 Decomposition of monthly runoff series with TVF-EMD method
2.2 TVF-EMD-LSTM 耦合模型的径流预测
选取长水水文站1987-2016年共360 个月的实测月径流数据,以1987年1月到2013年12月(共324个月)的数据作为训练集,2014年1月到2016年12月(共36个月)的数据作为测试集。图5 为原径流序列ACF 图和PACF 图,可以看出,ACF 的估计值在2 和6 时达到峰值,且PACF 的估计值落在95%的置信带内。考虑径流受降雨、下垫面等多种因素以及流域的实际情况的影响,选取滞时为6 个时段。表明在预测未来流量时,6 个前期流量与当前流量是相关的,且包含的信息更为有用,因此以每6个前期流量为一组作为LSTM 模型输入,以预报下一月流量值,以循环滚动进行预测。

图5 原径流序列ACF图和PACF图Fig.5 ACF and PACF of original runoff series
由于径流序列经分解后各IMFs特征各不相同,需考虑不同序列采用不同滞时。结合各IMFs 的ACF 图和PACF 图,各模型输入序列滞时t如下表1所示。输入时,各模型将序列x1、x2…xN(N表示为序列样本数)以t个值为一组,预测下一值,循环滚动预测,输入模型数据集可表示为:

表1 各模型输入序列滞时Tab.1 Delay number of input sequence of each model
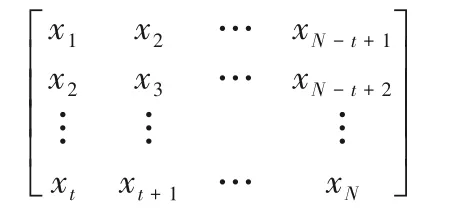
为了验证该模型预测结果的可靠性和准确性,选择与LSTM 模型、EMD-LSTM 耦合模型和CEEMDAN-LSTM 耦合模型3 种模型进行对比,LSTM 模型与其他耦合模型均采用与TVF-EMD-LSTM 模型相同的参数及变量设置。图6 为各模型测试集的预测值对比图。
由图6 可以看出:①单一LSTM 模型预测效果较差,只能显示序列大概趋势,预测值与观测值相差较大。②采用不同分解方法的耦合模型预测精度有显著的差别。TVF-EMD-LSTM 耦合模型预测精度明显优于EMD-LSTM 耦合模型和CEEMDANLSTM 耦合模型,EMD-LSTM 耦合模型预测效果较差。③TVFEMD-LSTM 耦合模型预测精度最高,预测序列趋势与原序列趋势基本相同,无相差较大值出现,说明TVF-EMD 有效缓解了EMD 和CEEMDAN 存在的模态混叠问题和噪声问题,更适合处理非线性非平稳的序列,并且能取得较好的预测结果。

图6 各模型预测值与原序列对比图Fig.6 Comparison between the predicted values of each model and the original sequence
为了更清晰准确地体现各模型的预测效果,采用五项模型评价标准来确定模型预测的精度,如表2 所列。由表2 可知:①在训练期,LSTM 模型各项误差指标最大,随着采用EMD、CEEMDAN 和TVF-EMD 方法后,各模型的MAE、RMSE和MAPE逐渐减少,且DC值均在0.7 以上,预测精度达到乙级以上;②模型验证期预测结果更能体现性能,TVF-EMD-LSTM 模型的MAE、RMSE和MAPE较LSTM 模型相比分别减少了84%、87%和84%,较EMD-LSTM 模型相比分别减少了72%、73%和80%,较CEEMDAN-LSTM 模型相比分别减少了69%、67%和66%。且TVF-EMD-LSTM 模型的DC值为0.98,预测精度为甲级,相比于EMD-LSTM 和CEEMDAN-LSTM 模型精度能有效提高。因此,TVF-EMD-LSTM 模型的预测结果具有更高的精度。③基于径流序列具有非平稳性和多频性,且序列中多含有噪声的特征,直接进行预测会影响LSTM 模型的拟合效果。EMD 分解存在模态混叠问题且无法消除序列存在的噪声,高频序列可能掺杂低频序列,对预测结果影响较大。CEEMDAN 解决了EMD的模态混叠和存在噪声问题,有效地提高了模型的预测精度,但并不能适应序列的特征且对参数有较高的要求。从验证期的结果来看,TVF-EMD 具有较好的分解效果,它既解决了EMD存在的模态混叠和噪声的问题,又使序列具有时变性,更好地将序列分解为高频序列和低频序列,使TVF-EMD-LSTM 模型预测结果精度最高。这说明,TVF-EMD-LSTM 模型具有较高的可行性和可信度,适用于预测非平稳、非线性、复杂多频的径流时间序列。

表2 各模型评价标准计算结果Tab.2 Calculation results of each model evaluation standard
综上所述,可将4 种模型的预测精度由高到低排列为:TVF-EMD-LSTM >CEEMDAN-LSTM >EMD-LSTM >LSTM。TVF-EMD-LSTM 模型相比于其他3种模型,在训练期和验证期都具有较高的精度,因此该模型可有效的对径流序列进行预测。
3 结论
为解决现有模态分解方法分量中存在噪声和模态混叠的问题,提高模型预测精度,本文提出了将TVF-EMD方法应用于径流预测的数据预处理中,并结合LSTM神经网络模型,以洛宁县长水水文站为例进行了月径流预测及对比验证,主要结论如下。
(1)TVF-EMD 方法更适用于非线性非平稳的径流序列,该种方法能够适应序列特征,通过时变滤波器更好地缓解了模态混叠问题,且保留了序列的时变性,能有效提高预测精度,为径流序列的预处理开辟了新方法。
(2)所采用的耦合模型的预测精度远远大于原模型,证明了对径流序列预处理的必要性,通过“分解—预测—重构”模式进行径流预测,可使预测精度有效提高。
(3)对比分析的结果表示,本文提出的TVF-EMD-LSTM 模型预测精度优于LSTM 模型、EMD-LSTM 模型和CEEMANLSTM 模型,并且较大误差出现的概率明显降低,预测精度大幅度提高,验证了所提出耦合模型预测的有效性,可为径流预测等相关工作提供一定的技术参考。
(4)本文提出的TVF-EMD-LSTM 神经网络耦合模型,有助于提高径流预测精度,是一种有效和可行的预测方法。然而,本文只考虑了月时间尺度的效果,今后可对不同时间尺度的径流序列进行预测,以验证该耦合模型的普遍适用性。□
