非承载桩稳定性实验研究
2022-02-23宋照明刘善均李雅琪刘帮玉
宋照明,刘善均,李雅琪,刘帮玉
(1.四川大学水力学与山区河流开发保护国家重点实验室,成都610065;2.烟台市河长制服务中心,山东烟台264010)
0 引言
为兴水利,河道中常修建不同的水利工程来控制和调配自然界的地表水和地下水。但在河道中修建闸、坝等泄水建筑物后,水流的水力特性会发生极大变化,其携带的能量较大且集中。类似变化将对河床、坡脚产生严重的冲刷破坏,因此水利工程中常修建护坦、护坡、海漫等防护建筑物。水流流经此类防护建筑物时,其破坏能力大幅减弱,但仍会对防护建筑物末端基础造成一定的掏刷,最终导致其薄弱部位被掏空,发生失稳破坏,威胁着大坝的安全。
水利工程中常采用抗冲桩来解决以上问题,其原理为利用流体流经桩时产生的绕流作用,使得桩对水流产生阻力作用,进而起到消能防冲的效果[1]。但目前水利工程中采用的抗冲桩多承载桩,即承受轴向力的抗冲桩。此类抗冲桩施工工艺复杂,且工程成本较高。
针对提高河床抗冲稳定性,减少基础淘刷破坏,同时降低工程成本,提高工程效益,本试验提出一种新型抗冲桩,即非承载桩。非承载桩只承受水平力,不承受轴向力。其常采用嵌入河床的方式,布置在护坡、护坦、海漫等防冲建筑物下游。当其嵌入到河床中时,只有露出床面的桩头受到来流作用力,嵌入到河床的部分基本不受冲刷,具有较好的稳定性。同时由于此类非承载桩仅嵌入河床维持自身稳定,相比于灌注桩等能够极大程度降低工程造价,提高工程效益。
1 试验设置
1.1 试验模型
试验用水槽为顺直矩形水槽,分为上游段与下游段,位于四川大学水力学与山区河流开发保护国家重点实验室内。水槽上游部分长3 m,距离进口1 m 处设可调整开度的闸门,从而能够保证试验段来流稳定且水深可控;为保证上游来流产生的冲坑充分发展,同时方便观察及研究,水槽下游长2 m,下游底板高程较上游底板高程低20 cm,采用粒径1 mm 细沙从底板起铺至与上游段底板齐平,即铺沙厚度为20 cm。下游段末端设有拦沙坎及沉沙池。水流经由水泵实现循环供给。试验模型布置图如图1所示。

图1 试验模型布置图Fig.1 Model layout
由于本试验中水流宽深比过小,关于边壁效应的影响不可忽略。为尽量降低边壁效应带来的影响,降低边壁摩擦阻力,使水流流动更加均匀平顺,降低误差。首先,水槽全槽由钢化玻璃拼接而成,用此材料也便于观察与测量;同时根据式(1)计算出为避免边壁效应水槽应具有的最小宽度[2],

式中:B为水槽宽度允许的最小值;r0为圆柱半径。
本试验用桩为混凝土浇灌而成的细圆柱体,直径d0=2 cm,容重rc=2.335 g/cm3,由模具统一制作而成。计算得到边壁效应影响范围B为20 cm。为更好地排除边壁效应的影响,尽可能提高试验精度,本试验水槽宽度设为1 m,桩从距水槽边壁15 cm处开始布置,桩间距离设为5 cm。
流量采用矩形薄壁堰测量,量堰在各级流量下水流平顺,最大测量范围满足试验最大流量要求[3]。试验流量精度控制在±1%以内,量水堰水面波动小于±2 mm,量筒内水位波动小于±0.2 mm,测针读数精确至±0.1 mm。流速采用LGY-Ⅱ型智能流速仪测量,测量精度为0.5 cm/s,测量范围为1~4 m/s;抗拔力的测量方法为将桩群插入试验用床体中,匀速垂直向上拉动单根桩体,读取拉力数值并记录,测十组数据,在其中去除一个最高值和一个最低值后,取剩下八组值的平均值;长度采用精度为1 mm钢尺测量。
1.2 工况设置
由于桩群阻力与水流雷诺数、水深、桩面粗糙度等有关,同时水深又会通过影响泥沙临界起动流速,继而影响桩群周围河床冲淤,因此水深桩径比是影响抗冲桩局部冲刷的一个重要因素。混凝土桩由模具统一制作而成,桩面粗糙度及桩直径差异不大可作为不变量。根据实际工程经验,试验混凝土桩长度从6 cm 到13 cm 每增加1 cm 做一组试验,每组试验对应5、8、11 cm 3 种闸板开度,闸后水深分别为4、5 和7.5 cm,记录流速、水深及拉力。
1.3 预试验
在试验正式开始前,先进行了预实验,即采用长度为15 cm的桩群,放置在距离尾坎不同位置处,以寻找单排桩群最适宜的嵌入位置。根据预试验结果结合文献查阅情况,本试验将桩群与尾坎之间距离设置为40 cm,此40 cm 表面铺设1 m×0.4 m灰塑板,并与上游底板高程齐平,用以模拟护坦等防冲建筑物,下游铺设桩体,桩体略高于灰塑板顶部,以起到稳定作用。通过试验观察,桩后冲坑的深度随时间变化符合大量试验成果验证的对数函数增长规律,即开始时,冲坑深度随冲刷时间增长而迅速增加,随后深度随时间变化趋于平缓,最终稳定在某一深度。同时在预试验中发现,当桩长度为15 cm 时,来流流速增加到2 m/s 时桩未见松动迹象,此流速换算到实际水利工程中较大,不具有普遍适用性,因此后续试验桩长度从13 cm 开始变化。
2 试验结果与分析
由于本文提出的非承载桩仅起到稳定作用,允许混凝土桩有一定程度倾倒,只要没有大部分倒塌的现象,即认为其依旧起作用。因此本文所有数值均在保证来流稳定基础上,桩群大面积倒塌时测得。
2.1 起动流速变化规律
水流能够直接对河床质产生拖拽力,此拖拽力可通过水流速度反映出来,由此产生了起动流速这一概念,起动流速指床面泥沙颗粒从静止状态转入运动状态的临界水流平均速度,它与块体自身的重力有关,计算常采用伊兹巴斯公式[4]:

式中:v为截流材料的极限抗冲流速;d为截流材料当量球直径;γs为材料的密度;γ为水的密度;g为重力加速度;k为综合稳定系数,同块体体积、形状、容重等特性相关。
表1 为0.04、0.05 和0.075 m 水深时不同长度的桩以及无桩时所对应的实测起动流速值,图2所示为增加非承载桩后的实测起动流速值变化趋势。

表1 实测起动流速值 m/sTab.1 Measured incipient velocity

图2 起动流速变化趋势Fig.2 The trend of starting velocity
分析数据发现,无桩时起动流速小,而当嵌入河床中桩长度越长,桩群大面积倒塌所需要的流速越大,稳定性越高。原因可以由前文桩基稳定基本分析得出,首先,随着桩长度增长,混凝土桩重力在不断增大;其次由式(3)看出,在桩直径一定的情况下,桩体所受摩擦阻力与桩底端至地表的深度呈直接正相关。嵌入河床中桩长度越长,桩体重力及所受摩擦阻力均在变大,因此桩体抗冲能力将增强,反映到抗冲流速也将增大。
同时分析测量数据发现,在同一桩长度下,水深越大,桩群大面积倒塌所需要的流速越大,稳定性越高。分析原因主要与流速随深度变化规律有关,某水深y处流速随水深变化公式[5]:

式中:Um为液面流速;y为距床面高度;H为水深。
由上式可知,在桩长度以及露出河床长度相同的前提下,桩倒时桩头出露部分所受力将不会相差太大,则此处位置流速也将不会相差太大,反应在距离河床位置y处流速相同。当水深增大时,若要保证y处流速基本相同,则Um必随之增大,断面平均流速也将随之增大。
从起动流速的变化可知,桩长度越长,起动流速越大,即桩的稳定性越好,因此在工程效益的允许的前提下,较好的桩长度为13 cm。
2.2 伊兹巴斯公式计算起动流速
起动流速同块体重力相关,伊兹巴斯公式中已考虑到不同材料容重影响,关于当量球直径d′可由下式求得:

表2 为求得的混凝土桩对应的当量直径,以及将此当量直径带入伊兹巴赫公式求得的起动流速值与试验实测流速值。

表2 计算与实测起动流速值对比Tab.2 Comparison of calculated and measured incipient velocity
分析表格中数据可以得出,试验实测流速是计算所得流速的4~6.5 倍。原因是由于上述计算公式中采用的综合稳定系数适用于孤立体河床质,而本文提出的非承载桩则是嵌入河床中,只有出露的桩头部分受到水流作用,大部分桩体则埋入河床中,埋入河床中桩体相比于孤立体将会额外受到四周砂卵石给予的摩擦力,相比孤立体更加稳定。通过上述对比分析,可以认为由于嵌入河床中,本试验提出的混凝土桩相比于河道中的混凝土块体抗冲能力有显著的增强,稳定性明显提高。
2.3 混凝土桩综合稳定系数kc
根据上述分析易知,关于河床混凝土块体的稳定系数已不适用于本文提出的新型非承载抗冲桩,因此本文通过以下分析对伊兹巴斯公式中的综合稳定系数做出补充与完善,得到适用于本文混凝土桩的综合稳定系数kc。
通过混凝土桩的伊兹巴赫公式:

得混凝土桩综合稳定系数:

式中:kc为混凝土桩综合稳定系数[无量纲];v为试验实测流速;γc为混凝土桩容重;d′为当量球直径。
不同工况下利用式求得d′带入式(7)求得kc如表3所示,kc的变化趋势如图3。

表3 混凝土桩综合稳定系数Tab.3 Comprehensive stability coefficient
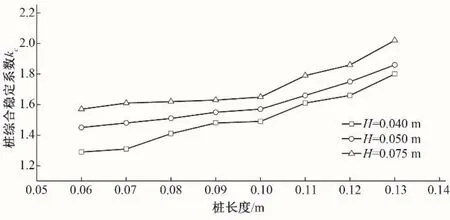
图3 kc变化趋势Fig.3 The trend of kc
分析上表可知,当试验中,混凝土桩长度在0.06~0.13 m 范围内变化,水深在0.04~0.075 m范围内变化时,混凝土桩综合稳定系数kc在1.29~2.02范围内变化。且随着混凝土桩变长,其综合稳定系数在不断变大;随着水深的增大,混凝土桩综合稳定系数也在不断提高。
3 结论
本文提出一种新型抗冲桩,采用嵌入的方法保持自身稳定。通过试验分析,得出以下结论:
(1)在桩周砂土性质相差不大的前提下,本文提出适用于新型非承载桩的摩擦力系数a=15 000,综合稳定系数kc在1.454 6~2.015 5范围内变化。
(2)试验测量所得抗冲流速是利用伊兹巴斯公式计算所得流速的4~6.5 倍,说明本文提出的新型抗冲桩能够极大程度地提高抗冲能力,保护工程,减少冲刷破坏。□
