强化学习求解组合最优化问题的研究综述
2022-02-23陈智斌吴兆蕊
王 扬,陈智斌,吴兆蕊,高 远
昆明理工大学 理学院,昆明650000
在实际工程应用中,有一类优化问题需要从集合的所有组合中找出一个最优方案或编排,这类离散空间中的优化问题称为组合最优化问题(combinatorial optimization problem,COP)。组合最优化(combinatorial optimization,CO)的求解方法广泛应用于交通运输、管理、电力、航天、通信等领域,其快速求解具有重要的理论意义和实用价值。例如,车辆的调度、金融资产的配置、仓库货物存储和运输路线的设计等实际问题都属于COP 问题,随着这些优化问题实例规模的不断增大和实例中动态及随机因素的增加,传统方法的求解将耗费巨大的时间,问题结构一旦发生变化,传统方法需要重新搜索求解,计算成本也会随之提高,快速求解这些优化问题变得十分困难。
近年来随着深度学习(deep learning,DL)技术在计算机视觉、自然语言处理、语音识别、推荐系统等领域的广泛应用,特别是深度强化学习(deep reinforcement learning,DRL)在AlphaGo、AlphaGo Zero的成功应用,表明在没有人类干预和指导的前提下,DL 和强化学习(reinforcement learning,RL)的结合仍然能够取得很大的成功,甚至超越了人类经验的指导,具有快速求解、泛化能力强、求解精度高等优势,为求解COP 问题提供一个全新的思路方法。鉴于此,近年来涌现出许多采用RL 求解COP 问题的新方法,即利用RL 训练模型的方法替代传统算法,让机器从算法中学习算法,从而快速且有效地解决实际问题,适应现代科技的发展,进而满足人类生活需求。
业界相关的工作已经逐渐开展,如2017 年Hu 等人采用DRL 的方法求解三维装箱问题;2018 年Lin等人把RL 应用在共享出行中的车辆管理和派单问题上;2019 年Mao 等人将RL 的方法应用在分布式集群任务调度中;2020 年Mirhoseini 等人又将RL应用到芯片布局设计中。这些研究都是通过RL 的方法解决实际生活中的COP 问题,核心思路是:RL序贯决策的功能与具有序列决策性质的COP 问题有天然的相似性,RL 模型可以通过智能体与环境的不断交互,自身逐步积累经验来获取问题的一个较优策略,在少量样本甚至无样本的情况下,通过自学习的方式快速求解实际生活中的优化问题,从而得到优化问题的解,在求解过程中传统方法和新思路的流程如图1 所示。

图1 求解COP 问题的两种思路Fig.1 Two approaches to solving COP problem
RL 求解COP 问题是近年来一个新兴研究领域,目前系统的研究和综述较少,因此本文对RL 求解COP 问题的方法进行文献综述,回顾总结各类求解方法和应用研究,分析求解模型的优缺点,为各位学者在新兴方向的研究提供参考。
1 组合最优化问题和强化学习的介绍
1.1 组合最优化问题的简单概述
CO(又称离散优化)是最优化理论的一个重要组成部分,它是运筹学与计算机领域的一个交叉学科,主要研究具有离散结构的优化问题,即研究如何从一组有限的对象中找到一个最优对象的一类问题,这类问题的数学模型如下:

其中,为决策变量,为目标函数,为约束条件,为离散空间中有限点组成的定义域。
比较有代表性的几个COP 问题:旅行商问题(traveling salesman problem,TSP)、施泰纳树问题(Steiner tree problem,STP)、车辆路径问题(vehicle routing problem,VRP)、装箱问题(bin packing,BP)、背包问题(knapsack problem,KP)、平行机排序问题(parallel machines scheduling problem,PMSP)、最小顶点覆盖(minimum vertex cover,MVC)、集合覆盖问题(set covering problem,SCP)、最大割问题(max-cut)。
这些COP 问题普遍存在于日常的生活中,它们属于非确定性多项式问题(non-deterministic polynomial,NP),如何提高解的精度、减少时间复杂度、增强泛化能力、快速且有效地得到问题的较优解是长期以来最优化理论的热点研究课题,其中求解方法的选择显得尤为重要,本文会在1.2 节对COP 问题的求解方法进行总结。
1.2 组合最优化问题求解方法概述
(1)传统方法
①精确算法(exact algorithm):枚举法、分支定界(branch and bound,BB)、动态规划(dynamic programming,DP)等均是通过不断迭代的方式求解COP 问题的全局最优解。
②近似算法(approximation algorithm):贪婪算法、局部搜索、线性规划等可以在多项式时间内来近似最优解,保证最坏情况下给出的解不低于(最大化问题)最优解一定的倍数。
③(元)启发式算法(heuristic algorithm):遗传算法、蚁群算法、模拟退火算法等均可以针对一般的COP 问题求解。
上述方法通称为传统算法,以经典的TSP 问题为例,其中枚举法和DP 法求解TSP 问题的时间复杂度分别为(!) 和(2),随着实例问题规模的扩大,该方法很难快速求解大规模的TSP 问题,因此精确算法对求解COP 问题规模有一定的局限性;假定P≠NP,一般形式的TSP 问题是不可被近似的,设计近似算法多数要考虑问题的特殊情况,因此近似算法对求解COP 问题的条件有一定的限制;蚁群算法等可以快速求解TSP 问题,但缺乏理论支撑以及无法保证解的全局最优性,导致启发式算法很难保证求解的质量。
(2)基于机器学习的COP 问题求解方法
①基于神经网络(neural network,NN)求解TSP问题:Hopfield 等人提出一种Hopfield 网络,首次尝试用机器学习(machine learning,ML)的方法求解小规模的TSP 问题,之后很多相关工作也相继出现,早期采用NN 求解COP 问题的文章可见Smith的综述。
②基于指向型网络(Pointer network,PN)求解COP 问题:Vinyals 等人针对Seq2Seq序列模型输入输出维度是固定的问题,对其改进,提出PN 架构,并加入注意力机制(attention mechanism,AM)使得序列模型不受输入输出维度的限制。PN 架构为基于ML 等新方法求解COP 问题的工作奠定了很好的理论基础。
③基于DRL 求解COP 问题:监督学习(supervised learning,SL)需要大量标签,且COP 问题的高质量标签不易获得。RL 使智能体与环境不断交互,通过奖励值来激励学习得到数据,克服了SL 中大量标签的花费问题。Zhang 等人将RL 应用到NP-hard 的车间调度问题,Bello 等人提出神经组合最优化模型(neural combinatorial optimization,NCO),为后续基于RL 方法求解COP 问题的推进奠定了基础。
④基于Transformer框架求解COP 问题:Transformer 框架延续了AM 中编码-解码的结构,其网络架构均由自注意力机制和全连接层(fully connected,FC)组成,模型中多重注意力机制(multihead attention,MHA)的自注意力机制计算方法,增加更多计算层,以便提取到深层节点的特征信息,有效克服信息丢失问题。
⑤基于图神经网络(graph neural networks,GNNs)求解COP 问题:GNNs 近几年发展迅速,是一种将深度神经网络(deep neural network,DNN)模型应用于解决图上相关任务的方法,通过低维的向量信息来表征图的节点及拓扑结构,此方法可以很好地处理非欧几里德数据,有效抽取图结构中的关键节点信息。
⑥基于ML 与传统方法结合的求解方法:此方法求解COP 问题主要是端到端的输出解。针对搜索过程中子问题不同的特性,Liberto 等人提出DASH(dynamic approach for switching heuristics)架构,动态切换合适的启发算法求解COP 问题。He 等人引入模仿学习(imitation learning,IL),以SL 的方式得到自适应的节点搜索策略。此方法能够利用ML 方法的优点,同时还能保证传统方法的最优性。
近年来采用ML 方法求COP 的方法逐渐增多,其中Bengio 等人的综述介绍了ML 与COP 求解的方法导论,说明ML 方法可以求解部分COP 问题,这对COP 问题的求解提供了部分理论支撑。文中表1 分析并总结了基于RL 的COP 问题求解方法,图2 汇总了求解COP 问题的方法框架。

图2 COP 解决方案框架Fig.2 COP solution framework

表1 研究方法、求解问题、模型算法的分析与总结Table 1 Analysis and summary of research methods,solving problems and models
1.3 强化学习的简单概述
RL 被定义为智能体与环境不断交互,获取相应的奖励,不断学习以完成特定的目标任务。从图3可以理解为智能体在与环境进行交互的过程中,通过不断的尝试,从错误中学习经验,并根据经验调整其策略,来最大化最终所有奖励的累积值。RL 的奖励很重要,具有奖励导向性,这种奖励导向性类似于SL 中正确的标签,从一开始没有数据和标签,不断尝试在环境中获取这些数据和标签,然后再学习哪些数据对应哪些标签,通过学习这样的规律,不断更新智能体的状态,使之尽可能选择高分行为。RL 不是简单学习运算一个结果,而是学习问题的一种求解策略。

图3 强化学习简要模型Fig.3 Brief model of reinforcement learning
DRL 是DL 和RL 的结合,同时具有感知能力和决策能力。具体来说,DRL 通过RL 来定义问题本身和优化目标函数,DL 来解决状态表示、策略表达等问题,DNN 来拟合RL 中的值函数、策略,然后采用误差反向传播算法来优化目标函数。DRL 是一种端到端的感知与控制系统框架,一种更接近人类思考的ML 方法。从图4 可以看出,DRL 结构与RL 结构类似,为解决复杂决策系统提供方便。

图4 深度强化学习简要模型Fig.4 Brief model of deep reinforcement learning
RL 根据马尔可夫决策过程(Markov decision process,MDP)可以分为基于模型的RL 算法和无模型的RL 算法,其原理分别是基于DP 和蒙特卡罗方法,RL 算法的具体分类见图5。

图5 强化学习主流算法Fig.5 Mainstream reinforcement learning algorithms
(1)强化学习
RL 可以建模为一个MDP,其过程可以用五元组(,,,,)表示。其中表示环境的状态集合,表示智能体的动作集合,是各个状态的转移概率,是采取某一动作后到达下一个状态的奖励值,是折扣因子。
MDP 可表示成:

的概率:

给定策略(|),智能体与环境一次交互过程的轨迹所收到的累积奖励为总回报:

其中,∈[0,1]是折扣率,当接近于0 时,智能体会注重短期回报,而当接近于1 时,智能体会注重长期回报。
最优策略是每个状态所获得的总回报最大的策略,最优策略的目标函数为:
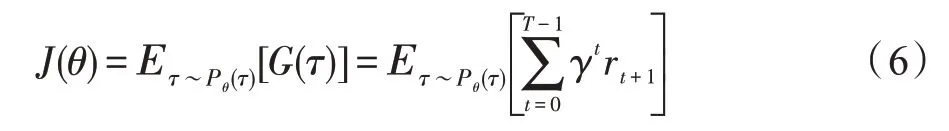
(2)基于策略梯度的深度强化学习
基于策略梯度(policy gradient,PG)的DRL 常应用于状态空间过大或连续空间的RL 问题上,它不需要计算值函数,可以用DNN 来表示从状态空间到动作空间的一个参数化映射函数=π()。策略搜索是通过寻找参数使得目标函数π()输出概率最大,直接计算与动作相关的PG,沿梯度方向调整动作,好的行为会增加被选中的概率,不好的行为会减弱下一次被选中的概率,是一种端到端的输出形式。
通常选择随机梯度下降(stochastic gradient descent,SGD)的REINFORCE 算法对策略的参数进行训练优化:

其中,(τ)为作为起始时刻收到的总回报。
采用REINFORCE 算法求解TSP 问题会导致不同路径之间的方差很大,从而模型结果难以收敛,这是高维空间中使用蒙特卡罗方法普遍存在的,为此引入一个和a无关的基准函数(s)来减小PG 的方差,其中(s)和(τ)相关性越大效果越好,一个很自然的选择是令(s)作为值函数V(s),其中带基准线REINFORCE 算法中参数的值函数和策略函数的更新如下:

(3)基于值函数的深度强化学习
2013 年Mnih 等人提出深度Q-网络(deep Qnetwork,DQN)算法,2015 年Mnih 等人又改进了DQN 算法,使其训练过程具有稳定性。此算法是DL与RL 的首次结合,采用DNN 端到端地拟合Q-学习中的Q 值,充分发挥出DNN 对高维数据处理的能力,其中关键的评估策略π(|)可分为两个值函数:状态值函数和状态-动作值函数。
状态值函数的策略期望回报可以分解为:

从状态开始,策略得到的期望总回报:

状态-动作值函数是指初始状态为并执行动作,然后通过策略得到期望总回报:

(4)基于行动者-评论家的深度强化学习
行动者-评论家(actor critic,AC)算法是结合PG和时序差分(temporal difference,TD)的一种RL 算法。行动者通过策略函数π(,)学习到一个更高回报的策略。评论家经由值函数V()表示,对当前策略的值函数进行估计,即评估行动者策略的好坏。借助于值函数,AC 算法可以进行单步策略更新参数,不需要所有回合结束再更新参数,如Lillicrap等人采用深度确定性策略梯度(deep deterministic policy gradient,DDPG)来实现AC 算法。
DeepMind研究人员基于AC 算法,提出它的变体A3C,即多个智能体并行学习,以固定的时间间隔但不同步地去探索环境,实时更新权重,然后让其主网络接受这些权重,这样每个智能体都可以改善主网络,并且智能体之间可以相互激励,以便更好地训练参数,增强模型的稳定性。针对A3C 算法智能体的异步性,DeepMind团队接着提出A2C 算法模型,其更新都是同步的,且均在较大批次上运行,这样可以更好地利用GPU 加速。针对训练过程中权重更新不稳定的问题,Schulman 等人提出近端策略优化算法(proximal policy optimization,PPO),修改了A2C 算法的损失函数,解决训练不稳定的问题。同时为了更好地激励智能体自主探索环境,加快训练速度,Haarnoja 等人基于AC 算法提出柔性行动者-评论家算法(soft actor-critic,SAC),它可以很好地学习奖励,还能最大化其行为的熵,即尽可能地让智能体的行为不可预测,同时还能获得更大的奖励。由于RL 中经常会出现奖励的稀疏性,这使智能体的学习效率很低,为此Pathak 等人提出Curiosity-based的探索算法,让智能体极端好奇地去探索环境,利用好奇心这一特性,让智能体尝试预测接下来的行为动作,并预测与结果不吻合的值,让奖励成为智能体固有的性质,而不是从环境获得,有利于智能体进行高性能计算。为了更好地理解RL 主流算法,可以参考刘全等人和Li对RL 的研究综述。
2 强化学习求解组合最优化问题的分析
2.1 组合最优化问题的求解难点
针对NP-难的COP 问题实例进行快速求解,传统方法是以设计近似算法为主,这类算法都是针对问题本身而设计的。首先需证明所求解的问题是存在近似算法的,比如:假定P ≠NP,一般形式的TSP 问题没有近似算法;NP 难解的KP 问题没有多项式时间算法;对任意的>0,BP 问题不存在近似比保证为3/2-的近似算法。其次考虑要求解的问题是否可以归约到其对偶问题上求解(利用线性规划的思想)。不论如何设计算法都需要对其正确性进行证明并找到合适的紧例子,才可以说明算法的严谨性及对算法的分析是好的,因此许多COP 问题的算法设计需要大量的人力和专家的经验。在未来,随着科技发展和进步,对求解各种COP 问题(变体问题)的要求会更高,在优化算法设计上要取得重大的突破也是困难的。
同时,针对同一个COP 问题的求解,常常会出现下述情况,先前的求解对后面问题的求解基本没有帮助,但是大多数优化问题又具有相同的优化结构,而传统算法的设计不仅没有很好利用相同问题之间的相似性,还难以考虑动态及随机因素,由此建立的数学模型泛化能力弱,不能很好地迁移到相同问题的不同实例上。比如为匹配(matching)问题和SCP问题设计近似算法时,会立即遇到下述困难,为确定近似比,会对算法产生的边费用以及最优解的边费用进行比较,其中不仅寻找最优解是NP 难解的,而且计算最优解费用也是NP 难解的,这正是此类问题的难点所在,即使通过确定OPT 的下界方法来保证近似比,还需寻找不同COP 问题的对偶问题,这个过程也是困难的。假如通过上述方法确定了下界,想要改进基数顶点覆盖的近似保证,这是不可能的,因为考虑二部图K给出的无限实例族,说明近似算法的分析是紧的,以这种OPT 的下界方式建立的近似保证,不可能设计出比它更好保证的近似算法。
随着人工智能、大数据时代的到来,COP 问题实例的规模不断增大,随之会出现“组合爆炸”的现象,相关问题计算的时间和空间复杂度会呈指数增长,传统方法很难快速求解大规模性的实际问题,即使解决了这类问题,求解时间和花费也是人们无法接受的。在权衡时间和精度的条件下,目前传统算法仍然是求解NP 问题的有效方法,但高效求解大规模COP 问题实例及其变体问题成为一个很大的挑战。在P ≠NP 的假设下,放眼国内外专家团队对COP 算法的研究,传统方法在短时间内不会取得重大突破,未来的发展是基于线下训练、线上求解的高性能计算设计上。
这款臻酿标志着Penfolds当代酿制工艺,突出地域特色的同时,也代表了法国橡木桶酿制赤霞珠的成熟技巧,既是Penfolds精巧技艺的映射,同时也是Penfolds对多样性的不倦追求。
2.2 强化学习求解组合最优化问题的优势
许多COP 问题都是NP 难解的,设计算法的过程本身难度就很大,且不容易被刻画,无模型的RL 方法可以通过智能体与环境的不断交互,学习到相应策略,模型训练完成后,短时间内给出一个高质量解,甚至比传统算法求解的质量要高。如Alipour 等人提出一种遗传算法和多主体RL 算法结合的混合算法来求解TSP 问题,文献[52]采用GA-MARL+NICH-LS 算法使得求解的精度高于几个传统算法;Fairee 等人提出一种采用RL 算法更新解的模型和基于人工蚁群的组合变体算法,文献[53]在6 个测试集上测试,在收敛速度上,RL 更新的解快于人工蚁群算法。
针对传统方法难以解决多维度的问题方面,RL可以采用值函数近似和直接策略搜索等算法,使问题的描述更加全面,从而得到更高质量的解。如Hu等人提出一种多智能体RL 框架求解多重旅行商问题(multiple traveling salesman problem,MTSP)。网络架构由GNNs 和分布式策略网络组成,利用RL 算法训练模型参数,采用S-样本(批次训练)的方法减少梯度方差,提高模型的整体性能。针对大规模问题求解,该框架学习的策略优于整数线性规划和启发式算法。
针对求解动态和受随机因素影响的问题上,RL可在智能体与环境之间的交互以及状态转移过程中加入随机因素,增强模型的鲁棒性,且模型一旦训练完成,对同一问题的变体,也可以很好地适应新数据的变化。如Yao 等人提出一种端到端的RL 框架求解COP 问题,核心思想是把状态空间作为问题的解,解的扰动信息作为智能体的动作空间。模型利用GNNs 抽取潜在的表征信息,对状态行为进行编码。推理阶段采用深度Q-学习改善解(转换或交换向量标签)的质量,得到问题的最优策略。在Max-cut 和TSP 问题上,此模型相比学习算法和启发式算法有更优的表现和泛化能力,更好地适应动态和随机因素。
目前,DL 的实验平台配置逐渐完善,如Pytorch、TensorFlow 等DL 框架,这些面向对象的开源库,降低了各位学者的使用门槛,还有硬件设施GPU、TPU 的快速发展,使得COP 问题会在更短的时间内得到显著的优化效果。利用RL 和计算机科学的这些优点,对求解路径优化、库存控制以及车间工件调度等COP 问题领域的大规模动态问题、随机决策问题、各种变体问题会更为有利,为COP 的研究提供一种新方法。虽然处于初级阶段,但也取得一定的成果,说明此方法求解COP 问题的可行性。具体来说,采用RL 求解COP 问题的优势总结如下:
(1)泛化能力的增强:传统方法对于一个新问题或者其变体问题,大多都需要重新设计新算法,然而ML 有让算法具有学习的能力,从算法中学习设计算法,替代手工设计算法。模型一旦训练完成,其参数可以相互调用,通过迁移学习的方式传递给相应的策略函数,从而在给定一个新问题时能够有效快速地获得解。
(2)求解速度的加快:传统的算法是基于初始解的迭代,RL 对一些COP 问题可以产生质量较高的初始解,不断更新解得到更优的解。DRL 采用DNN 对模型进行合适的特征表示,进而降低求解空间的大小,即减少了搜索宽度和深度。
(3)伸缩性的提高:RL 中一些算法可以降低COP 问题的时间复杂度,再结合GPU、TPU 的加速计算,使其应用于求解大规模的COP问题。模型一旦训练完成,可以适用于不同的COP 问题,无需为每个问题设计新的算法或重新建立新的模型,从而避免人力资源的浪费,为实时求解动态COP 问题成为可能,以便高效求解实际生活中所面临的众多NP-难问题。
(4)初始解的要求降低:DL 中的SL 需要大量训练数据作为标签,COP 问题中生成这些数据需要解决大量的NP 难问题,获得标签的代价是巨大的,限制了SL 的适用性。然而RL 在给定一组实例解时通过计算优化目标来评估解的质量相对容易,在大多数RL 的框架中,其目标是学习一种随机策略,以高概率输出高质量的解。训练出的模型可以在各种复杂的真实环境中更好地泛化,减少对数据标签的依赖和未知数据的扰动。
2.3 强化学习与组合最优化问题的结合分析
首先RL 用于序贯决策,即根据当前的环境状态做出相应的行为选择,并根据行为的反馈不断调整自身的策略,从而达到特定的学习目标。COP 问题即在离散空间中选择事件的最优次序、编排等,与RL的行为选择具有天然的相似性。以经典的TSP 问题为例,当任意两城市之间的距离与城市排列顺序无关时,定义环游长度如下:

首先将TSP 问题建模成MDP,再利用RL 相关算法训练参数,学习到一个最优策略(|)以较大概率输出路径长度最短的环游,该策略可以建模为:

其状态、行为、奖励、策略表示为:
(1)状态:已经访问过城市的坐标集合。
(2)状态转移:根据已经访问过的城市和城市的坐标计算接下来将要访问的城市概率。
(3)动作空间:第步将要选择的城市π。
(4)奖励:已访问过城市路径总距离的负数(最短路径)。
(5)策略:状态到动作的映射,即得到的是选择城市的概率p(|)。
通过这样的建模,简单地实现了RL 与COP 问题的结合,不断地训练相关参数得到更为准确的策略,为COP 问题求解提供一种全新的思路。
3 强化学习求解组合最优化问题的方法
目前基于RL 求解COP 问题的方法主要分为基于NCO 模型的求解方法、基于动态输入的COP 模型的求解方法、基于图结构模型的求解方法、基于RL结合传统算法的求解方法、基于改进RL 模型的求解方法等五大类,本文主要对以上方法的研究进行综述,对各类代表性研究所解决COP 问题的研究问题、算法模型、优化效果进行对比分析(见表1),并对不同方法局限性及使用场景的限制进行了综合评述。
3.1 基于神经组合最优化模型求解方法
为克服SL 样本需求的问题,Bello 等人把NN和RL 相结合,提出NCO 模型。文章以PN 为基础,采用REINFORCE 算法训练模型参数,将TSP 问题的每个实例作为一个训练样本,目标函数是实例中城市的最短环游长度。模型引入critic 网络为基准构建与策略网络参数无关的估值网络,降低训练方差,该网络使用均方误差(mean square error,MSE)评判估值网络和SGD 法来优化目标函数,还指出结合推理搜索的求解方式能进一步改善解的质量。由于评估一条环游长度需要很小的计算量,可以让模型输出更多候选解,然后在求解空间中找到最优解,加快求解速度。文献[32]的实验结果显示,NCO 求解100-TSP问题的环游长度优于Christofides算法和专业求解器,200-Knapsack 达到最优解。
针对传统的搜索方法依赖于启发式算法且在许多COP 实例中采用启发式算法求解速度慢等问题,Chen 和Tian对此提出NeuRewriter 框架求解COP问题,以迭代的方式不断改进问题的解直到收敛,从而加快求解速度。整个策略分为两部分:区域挑选策略和规则挑选策略。区域挑选策略用于选取当前状态(每个解是一个状态)要更改的区域;规则挑选策略用于选取重写的规则。文献[57]采用RL 中的QAC 算法训练模型参数。实验结果显示:简化表达超过Z3 模型;JSP 超过DeepRM 模型和专业求解器;CVRP 超越了部分基于ML 的方法,比基于启发式算法和DNN 直接生成解的质量要高。
为进一步提高模型的泛化能力,Joshi 等人结合SL 和RL 训练100-TSP 问题,测试模型在一个变化的图上,最大到500 个节点。在固定大小的图上,采用协同训练的方式会更接近最优解,用GCN 编码替代Transformer 架构编码对模型求解影响较小,还证明了模型的泛化能力取决于RL 模型中的学习范式。Joshi 等人之后改进NCO 模型,将小范围TSP问题泛化成求解大范围的TSP 问题(128 万个节点)。
Miki 等人针对经典的TSP 问题提出了DL 和RL 算法(EV-贪婪+EV-2opt)结合的框架。此方法采用卷积神经网络(convolutional neural network,CNN)将TSP 问题的最优路线作为图像进行卷积学习操作。推理阶段结合EV-贪婪和EV-2opt 算法,高效输出最优解,同时比较2opt 和S2V-DQN 算法在TSBLIB 数据集上的优化效果。文献[60]结合DL 和RL 模型在求解质量和速度上优于单个模型,通过SL 得到的解再结合RL 训练可以提高解的质量。
鉴于DNN 模型以端到端的方式输出问题的解,Li等人采用DRL方法近似求解覆盖商问题(covering salesman problem,CSP)。模型以PN为基础,利用MHA采集结构信息,加入动态嵌入模型处理动态信息,使用REINFORCE 算法训练模型参数。该模型下求解CSP 问题的时间比传统启发式算法(LS1、LS2)快20倍,相比PN、动态指向型网络、AM 模型有更好的收敛性,且模型一旦训练完成(时间较慢),可以泛化到多种类型的CSP 问题上。
上述PN 模型原理是将COP 问题的实例编码成向量,使其在隐藏层输出,最后解码时通过Softmax对向量进行处理,输出具体实例中较大的概率向量,且输出向量维度与输入向量维度一致,具体模型如图6 所示。
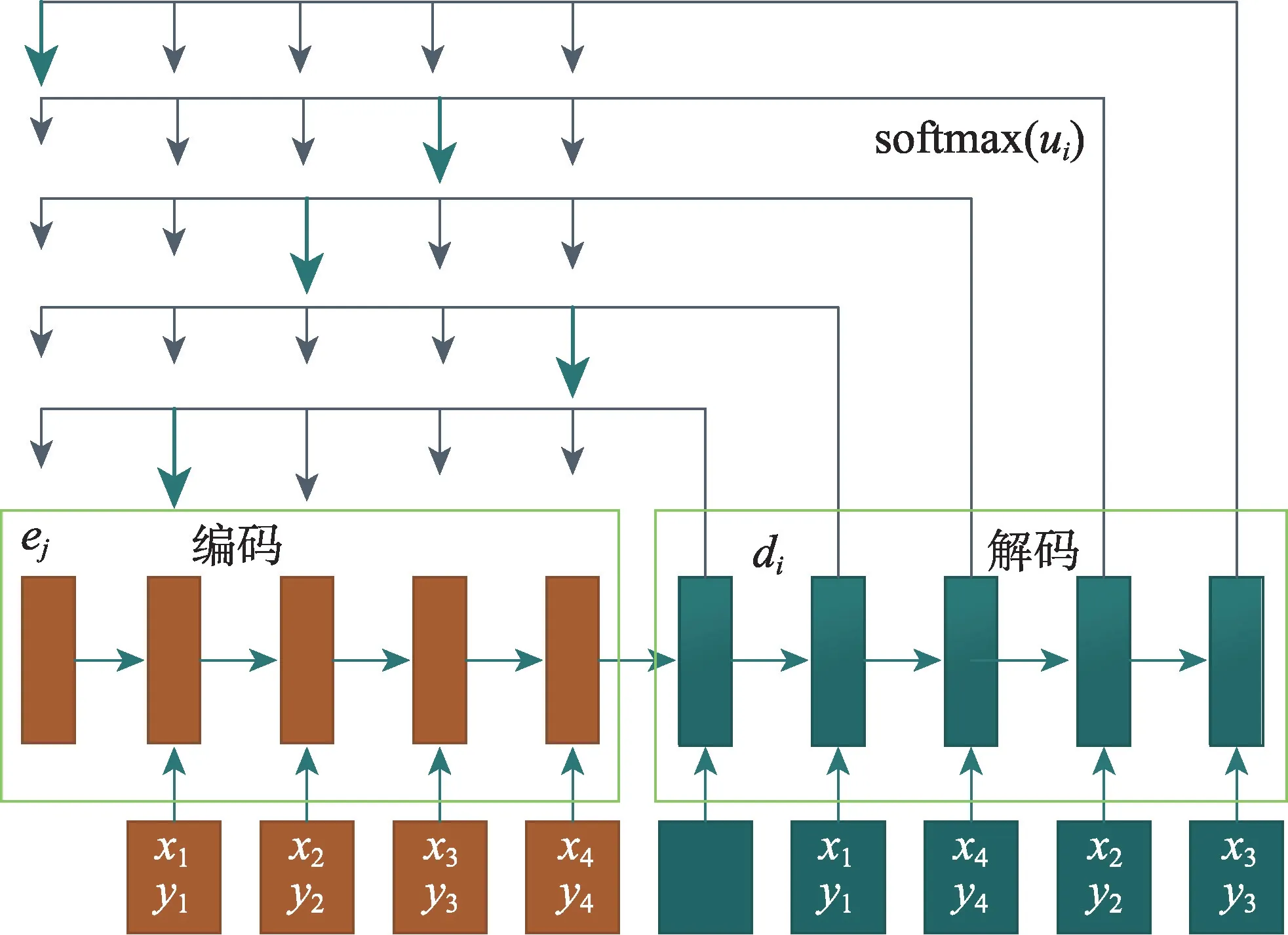
图6 Pointer networks模型Fig.6 Pointer networks model


表2 NCO 模型的局限性分析Table 2 Limitation analysis of NCO model
3.2 基于动态输入的组合最优化模型求解方法
针对VRP 问题的输入是动态变化的,使用PN 无法直接求解这类问题,Nazari 等人将PN 拓展成能够处理动态信息的COP 模型,采用一维CNN 替代编码输入层的LSTM,即替换编码部分,保留解码部分,这样使得模型的输出和输入的顺序无关,从而有效地解决动态问题的输入对问题求解的影响。模型的训练采用了经典的PG 方法,并加入贪婪算法和波束搜索(beam search,BS)两种推理技术提高解的质量。模型一旦训练完成,对于不同规模的实例,无需重新训练。文献[62]的实验是在50 和100 规模的VRP 问题上进行的,运用该模型在求解质量上相比经典Clarke-Wright savings heuristic、Sweep heuristic启发式算法有一定优势。推理阶段结合BS 后求解时间对比专业求解器有60%以上的优势。
鉴于Transformer 在语义信息深层特征的提取上有良好表现,Kool 等人改进其架构,编码部分中未采用位置编码,使节点嵌入与顺序无关。模型沿用了Transformer 架构中的MHA 和前馈FF 结构来得到每个城市对应的节点嵌入。解码采用了经典的自回归调整模式,并引入上下文节点来表征解码时的上下文向量,它包含了图嵌入层以及第一个节点(它是起点也是终点)与前一个输出节点的嵌入。最后解码结构加入一个单层AM(即=1 的MHA),通过激活函数softmax 输出,即为当前一步的输出。文献[63]采用经典REINFORCE 算法训练模型参数,其中基准函数通过策略模型进行确定的贪婪搜索得到。实验考虑了几种路径问题:TSP和VRP及其变体问题(SDVRP、PCTSP、SPCTSP),实验结果显示基于确定贪婪搜索的方法在求解质量和速度上优于先前端到端的模型,在100-TSP 问题上的优化性能超越了传统启发式算法,且模型的收敛性明显优于传统方法。
许多RL 模型会受到实例输入维度大小的影响,Emami 等人提出一种基于SPG(sinkhon policy gradient)算法学习策略模型,克服上述问题,并结合AC 架构求解COP 问题中的排列问题,该模型可以端到端地求解TSP 问题和Matching 问题,并把问题迁移到更大规模的图问题中求解。
更进一步,Oren 等人提出一个离线学习、在线搜索的框架(SOLO)求解COP 问题,该框架的求解过程可以看作一个MDP,采用深度Q-学习网络从图模型的状态行为空间中学习出一个最优策略,并结合蒙特卡罗树搜索(Monte Carlo tree search,MCTS)提升模型的稳定性和泛化能力等。文献[61]的实验在PMSP 和CVRP 两个COP 问题上进行,实验结果显示,该框架下在求解时间和模型的表达能力上超越了专业数学求解器和前沿的学习算法以及传统的启发式算法。
为了使智能体在每一个回合限制中可以探索动态的节点信息和隐藏层的信息结构,快速处理实例中的动态随机因素,Bo 等人提出动态的编码-解码架构,建立一个动态AM 模型求解VRP问题,文献[66]实验结果显示此模型求解VRP 的表现优于先前RL的方法且有很强的泛化能力。
上述模型中,AM 编码-解码的结构不受COP 问题输入和输出序列长度的限制,结合RL 算法后文献[62-66]中模型表现出显著的优势,可以广泛应用于求解COP 问题,具体模型如图7 所示。
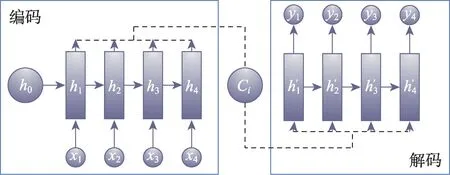
图7 Attention 模型示意图Fig.7 Schematic diagram of Attention model
2018 年Nazari 等人提出了一种求解具有动态因素COP 问题的模型,整体框架以AC 为基准,对PN 进行改进。借鉴循环神经网络(recurrent neural network,RNN)的原理,针对处理时间相关性较强的COP 问题,编码采用一维CNN 替代RNN 序列元素的嵌入。解码阶段利用AM 融合动态和静态的嵌入向量,最后通过softmax 函数进行归一化处理,从估值网络中得到每个输入元素的概率分布,再通过策略网络输出嵌入向量序列并进行加权求和,以较大概率输出解。针对RL 处理动态信息在决策过程中出现的不稳定性、有效节点信息的稀疏性问题,限制模型的优化效果,表3 分析了基于动态输入的COP 模型求解方法的局限性。
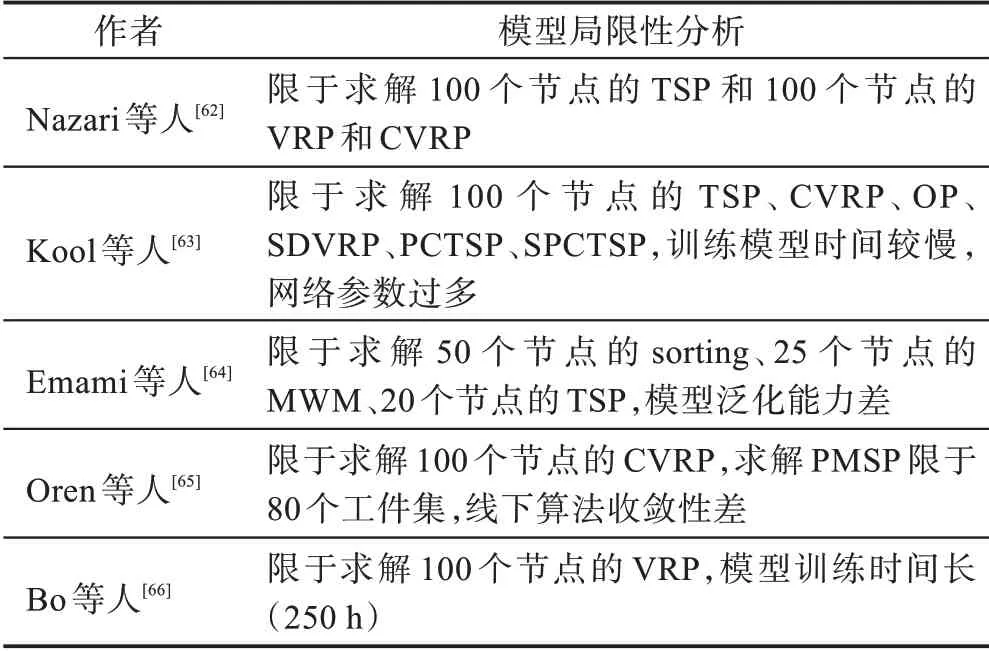
表3 动态输入模型的局限性分析Table 3 Analysis of limitation of dynamic model
3.3 基于图结构模型的模型求解方法
GNNs 是基于DL 的方法处理具有图结构信息的一种网络结构,通过聚合、更新、融合等操作对图结构进行特征提取,快速处理图数据。鉴于此,Dai 等人将RL 和GNNs 结合,提出一种新的优化算法(S2V-DQN),即将RL 算法与图嵌入结合,充分利用图中的特殊结构,让S2V-DQN 模型泛化到更多新问题的实例中。文献[67]利用GNNs 中S2V 的方法并配合使用RL 中Q-学习算法求解MVC、Max-cut、TSP问题。同时对比NCO 模型与启发式算法,该模型将TSP 和MVC 问题的规模分别扩大到300 个和500 个节点,同时可以将训练完成的图模型参数迁移到规模更大的图上(最大1 200 个节点)。
Drori 等人采用RL 训练GNNs 模型参数的方法,提出一种基于GNNs 的RL 架构,模型采用GAT编码,解码时加入Attention,求解MST、TSP、VRP 等经典COP 问题。文献[68]的实验训练过程在小图和随机图上,测试过程在大图和真实图上,最终使得所求解问题的近似比接近1。
针对处理百万级大小图上的困难问题,如何让算法解决训练集中类似分布的问题实例,并将之延拓到更大规模的问题(百万级节点)上,Mittal 等人提出GCOMB 框架(由SL 和RL 模型结合组成)克服上述问题,整个算法分为训练和推理两个阶段。训练阶段第一步通过SL 的方式训练GCN 中的参数,采用新的概率贪婪机制预测单个节点的质量和修剪不是解空间的集合,其本质上是让嵌入的点集合能够反映每个节点对于解的重要程度,用于构造嵌入输入;第二步采用RL 中Q-学习算法体系分析剩余高质量节点,把高质量解挑选出,作为COP 问题的解。推理阶段,先用训练完成的GCN 模型作为嵌入,然后通过Q-学习的Q 函数迭代计算问题的输出解,即用贪心算法以增量方式构造解。文献[69]的实验结果显示,此框架在求解最大流问题的速度上比最前沿的学习算法快100 倍,解的质量也略有提高。
为了更好解决具有图结构性质的COP 问题,Barrett 等人提出探究组合最优化(ECO-DQN)的方法框架,其模型架构由S2V-DQN、RevAct、ObsTun、IntRew 组成。其中S2V-DQN 是Dai 等人提出的方法;RevAct 指允许一个节点翻转多次仍可以被选择的操作;ObsTun 指求解状态包含7 个观察步骤,如基于顶点状态等,提供的信息呈现多元化,用于确定选取相应动作的价值,实时提供历史信息避免出现过拟合状况,在有限步的回合保证外部和内部奖励回报符合马尔可夫特性;IntRew 指通过奖励塑造的形式,当达到新的局部最优解时,给一个小的中间奖励作为内部奖励,很好地克服奖励稀疏的问题。文献[70]的实验结果显示,该框架下在Max-cut 上的求解效果优于SOTA 的RL 方法。该算法可以从任意的初始解迭代,因此可以与其他搜索方法相结合,进一步提升解的质量。
随着AlphaGo Zero的成功应用,Abe 等人将其思想延拓到COP 问题上,提出了CombOpt Zero 框架。模型利用MCTS 算法,在训练时提升了探索效率,增强了模型的泛化能力,在进行决策推理时增强了智能体的稳定性。一般的COP 问题与围棋相比有两点不同:一是状态由不同大小的图表示,通过GNNs 处理非欧几里德数据,能够抽取数据中的有效特征;二是获得奖励的值域不固定,文献[72]中通过回报归一化技术来解决。文献[72]还在网络模型中尝试不同GNNs 的变体模型,如图同构网络(graph isomorphism network,GIN)、不变图网络(invariant graph network,IGN)。实验在MVC、Max-cut、MC 问题上结果显示此模型的泛化能力优于S2V-DQN,且求解速度更快。
为了更好利用图模型的优势,Bresson 等人将Transformer 架构应用到求解TSP 问题上,模型采用RL 算法训练参数,通过自注意力机制编码,解码中加入BS 推理技术。文献[73]的实验结果显示,该框架的表现能力超越了基于学习的启发式算法,采样2 500 次后,50-TSP 问题的最优间隙为0.004%,100-TSP 问题的最优间隙为0.39%。
针对COP 中出现的大量与图模型相关的问题,采用GNNs对图模型进行预处理,文献[66-74]中GNNs架构对求解COP 问题显示出优异的效果,未来RL 和GNNs 模型的结合是一个较好的研究方向,GNNs 模型如图8 所示。
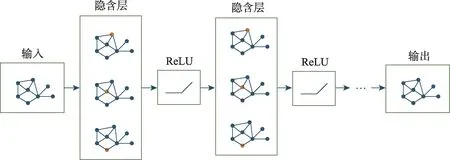
图8 GNNs模型示意图Fig.8 Schematic diagram of GNNs model
2017 年Dai 等人提出一种处理图结构的COP问题的新方法。模型框架在PN 架构基础上加入Attention、Transformer、GNNs 等结构处理图信息。编码-解码时,采用图嵌入操作,即将图中的顶点信息映射成一个低维稠密向量,保证在原图中相似的低维表达空间也接近,从而有利于信息提取。模型参数的训练大多采用Q-学习和Q-迭代的RL 算法,从而克服了奖励延迟问题,保证参数更新的稳定性和独立性。图的特殊结构可以承载更多的节点信息,让网络模型学习到有效的特征信息,从而扩大COP 问题的求解范围,同时图的拓扑性质导致RL 学习困难,巨大的解空间在搜索过程中也是困难的,限制了图结构模型的优化效果,表4 分析了基于图结构模型的求解方法的局限性。

表4 图结构模型的局限性分析Table 4 Limitation analysis of graph structure model
3.4 基于强化学习结合传统算法的求解方法
以PN 为基础的RL 模型在求解COP 问题上已经展现出良好的效果,为提高解的质量,Deudon 等人改进Bello 等人的NCO 模型,编码层延续了Transformer 架构,其编码的网络架构均由层叠的自注意力机制和逐点的全连接层组成,编码层没有使用LSTM 架构。此模型中采用自注意力机制替换Seq2Seq 模型中的Attention。在解码层改进策略网络,采用PG 和REINFORCE 算法训练模型参数。模型在解的质量与运行时间等方面的表现结果与Christofides算法的表现结果相当,可以快速求解大规模的路径优化问题。实验还将50-TSP 问题的模型参数迁移到100-TSP 问题上进行求解,其表现结果相当,说明该模型有很好的泛化能力。此外,推理阶段结合2-opt推理技术,可以快速提升解的质量,体现出ML 与传统算法结合的优势。
针对如何有效找到最优解的确界问题,Cappart等人提出一种利用DRL 来确定变量顺序的方法。决策图(decision diagram,DD)是一种分层的有向无环图,它得到的上界和下界比传统方法更好,由于界的质量又依赖于构建DD 过程中变量的选取顺序,采用NN 拟合Q-学习中Q 值的方法来确定变量顺序。文献[75]的实验数据表明此方法所确定变量顺序的结果比利用线性规划取得的更优。针对DRL 求解TSP 问题泛化能力弱且没有一个系统的方法去提高解的质量及无法有效证明近似比等缺陷,Cappart 等人又提出了一个基于DRL 结合约束规划求解COP问题的模型,为了更好地结合这两种方法,对于给定的COP 问题,首先采用动态规划的方法对问题进行建模,然后将模型编码成DRL 和约束规划可以学习的输入形式,在编码中加入约束规划可以更好地探索解空间,其中RL 中的网络使用了GAT 和Transformer架构作为图嵌入。文献[76]还考虑了三种约束规划搜索策略:BB、迭代有限差异搜索法(iteration limited discrepancy search,ILDS)、基于搜索的重新启动法(restart based search,RBS)。此方法求得的解与业界的专业求解器相比,在带时间窗的旅行商问题(traveling salesman problem with time window,TSPTW)和4-PORT 问题上有很好的优化效果,体现了DRL 结合约束规划的方法具有一定优势。
为扩大求解范围,Gao 等人采用AC 框架去学习一个局部搜索启发式算法求解VRP 问题,模型通过GAT 进行编码操作和使用GRU(gate recurrent unit)架构进行解码操作。两者结合的学习方式可以解决大规模(400 个节点)的VRP 问题,优化效果超过其他传统的启发式算法。
更进一步,Costa 等人提出一种由DRL 的方法学习2-opt操作的局部搜索启发式算法。模型为一个策略神经网络,即采用PG 算法学习2-opt 操作,从随机策略得到一个循环解,采用点注意力机制,使模型更容易拓展到更一般的情形k-opt 操作。文献[78]的实验结果显示,此模型学习到的策略与先前的DL 方法对比,该方法会以更快的收敛速度逼近问题的最优解。
在RL 算法的基础上,为提高模型的伸缩性和鲁棒性,Zheng 等人基于变邻域搜索和LKH3 算法,提出一个VSR-LKH 新框架求解TSP 问题。该框架采用Q-学习、Sarsa、蒙特卡罗三个RL 算法取代LKH3算法的遍历操作,即让训练好的模型自动挑选适合的边加入到候选集合中。实验结果显示,在TSPLIB数据集上测试,该方法求解的精度超越了传统的LKH3 算法。
该思路是近年来诸多学者尝试的一种新方法,在RL 中加入传统算法构造解的方法已经在COP问题中取得较好成果。文献[52,54,74-79]中的方法大多数还是需要结合一些传统的方法,如经过贪婪搜索、2-opt 操作、BS、采样(sampling)、LK 等处理后,解的最优间隙会随之降低,进一步加快搜索时间和提升解的质量,甚至会超越传统的SOAT 模型。RL结合传统方法的策略表明目前的模型仍然有较大的优化空间,其中RL 模型学习效率低、收敛慢等问题会对COP 问题的求解造成影响,表5 分析了基于RL结合传统算法模型的求解方法的局限性。
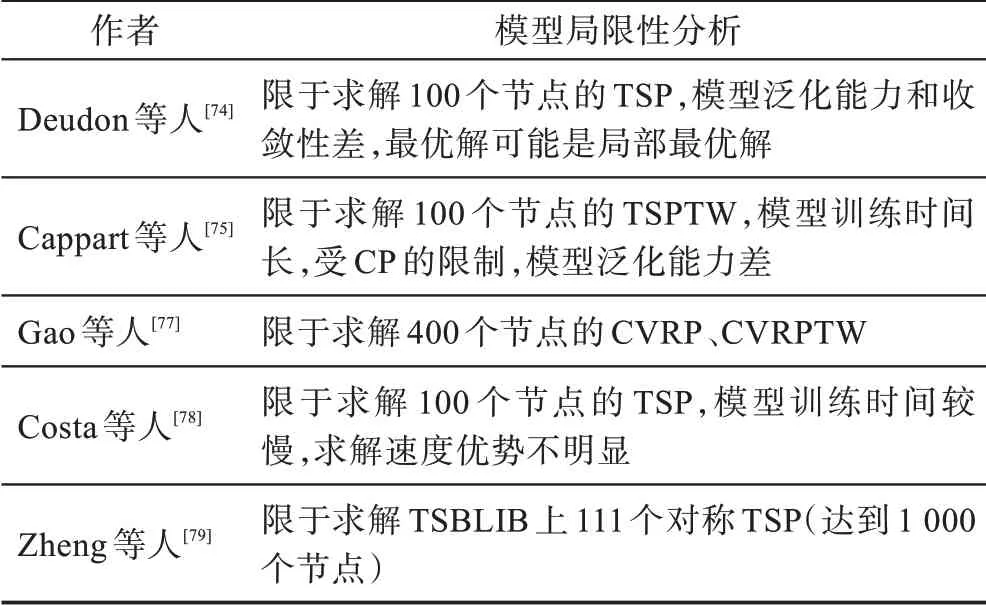
表5 RL 结合传统算法模型的局限性分析Table 5 Limitation analysis of RL combined with traditional algorithm model
3.5 基于改进强化学习模型的求解方法
针对LHK 和传统算法中出现的求解速度慢及求解节点稀疏等问题,使用经典RL 模型不能很好选择高质量解,为此Lu 等人改进框架结构,首次提出一种基于学习迭代的方法求解CVRP,采用分层和REINFORCE 算法训练模型。文献[81]中模型优化后的解在速度上超越传统算法,并且求解100-CVRP 问题上达到了目前最好的结果(平均花费15.57)。
针对进化算法无法解决大规模优化问题的缺陷,Li 等人改进框架结构,提出一种基于DRL 解决多目标COP 问题的框架(DRL-MOA),在PN 中融入分解策略和邻居多参数传递策略,采用AC 算法训练模型参数。文献[82]的实验结果显示,该模型下求解动态TSP 问题、多目标TSP 问题的速度和泛化能力超越NSGA-Ⅱ、MOEA/D、MOGLS 等经典多目标优化模型。
为了让智能体快速、准确调整自身的行为(通过环境和其他智能体的交互),Silva 等人对智能体改进,加入一个新的自适应技巧,提出多元启发式算法优化多元智能体的框架(AMAM)。文献[83]的实验结果显示,VRPTW 和UPMS 两个COP 问题在AMAM框架下求解的质量优于其他传统算法和单智能体优化框架。
更进一步,Tassel 等人提出一个高效的DRL 模型求解PMSP 问题,该模型以端到端的形式输出解,即在一个时间方案的限制下,模型可以自动地学习调度工作方案。文献[84]的实验结果显示,该方法的表现超越了现有的DRL 方法,接近于当前SOTA 传统COP 问题的求解方法。
针对现有框架难以求解大规模TSP 和TSPTW问题,Ma 等人改进框架结构,提出图指向型网络(graph pointer network,GPN)架构。具体采用分层强化学习(hierarchical reinforcement learning,HRL)训练模型参数,编码由点编码和图编码两部分组成,点编码依赖于LSTM 架构,由此得到城市的点嵌入,图编码依赖GNNs 架构,得到城市的图嵌入。解码过程中加入Context vector操作后,使得attention 更好地分配到相应节点,高效输出COP 问题的最优解。文献[85]的实验结果显示该模型下求解小规模(50/100个节点)TSP 问题的模型参数可以很好地迁移到大规模(500/1 000 个节点)TSP 问题上,说明此操作提高了GPN 模型的泛化能力。此方法求解TSPTW 问题在时间和精度上超越了专业求解器和蚁群算法。另外,实验证明了分层图指向型网络(hierarchical graph pointer network,HGPN)模型的优化效果和收敛速度均优于GPN。
Delarue 等人提出一种基于值函数的RL 框架(RLCA-16)求解CVRP 问题。该框架下每步更新考虑单个距离,而不是等待模型训练完成后获取距离,通过一个直接的策略迭代更新每步距离。文献[86]在CVRPLIB 数据集上测试,实验结果显示,相比其他RL 算法和传统运筹优化算法有较好的效果,该模型平均最优间隙达到1.7%,并将此模型推广到求解PCTSP 问题上。
该思路是近年来诸多学者进一步求解COP问题的一种新方法。针对目前RL 模型存在训练的不稳定性和输出难以收敛的问题,可以通过不断改进RL 算法或者采用更多复杂DRL 的方法,更好地适应各类COP 问题的求解。现有DRL 模型中难免会存在价值网络、策略网络奖励机制构造不合理的情况,网络结构的瑕疵会对求解的质量造成影响,表6 分析了基于改进RL 模型的求解方法的局限性。

表6 改进RL 模型的局限性分析Table 6 Limitation analysis of improved RL model
3.6 经典COP 问题的实验对比
由于TSP 是COP 问题中的经典问题,TSP 又是VRP 的特例,这两个问题都是运筹学和CO 领域的热点问题。基于RL 求解COP问题的方法在TSP、VRP以及它们的变体问题上已经取得较好结果,相比传统算法,该方法是近年来研究的热点内容。表7、表8对上述求解方法在不同规模TSP、VRP 上的优化效果进行实验对比,实验数据来自各个文献的实验结果,均通过Pytorch、TensorFlow 深度学习框架实现。

表7 不同模型在TSP 上的优化效果比较Table 7 Comparison of optimization effects of different models on TSP

表8 不同模型在VRP 上的优化效果比较Table 8 Comparison of optimization effects of different models on VRP
通过实验结果比较可以看出,Joshi(BS)和Costa的方法在20-TSP 问题上与专业求解器的优化效果基本相同,但运行时间相对较慢。Kool(GS)的方法可以在短时间高效求解,但精度略低于最优解。Bresson的方法可以达到最优解,求解速度超越了传统的优化器和目前的SOTA 模型,但求解范围有限。总体来看,目前RL 方法求解TSP 在精度、泛化能力等方面有许多问题待解决,仅仅在推理速度方面超越目前最先进的求解器Concorde、Gurobi、OR-Tools。改进Transformer 架构以及结合GNNs提升模型稳定性是未来一个重要的研究内容。
通过实验结果比较可以看出,Lu和Chen的方法在精度上超越了LKH3 和OR-Tools 等专业求解器,运行时间慢于OR-Tools。Kool的贪婪搜索方法在几秒内可得到近似解,适用于在线快速求解。近年来多数采用RL 结合传统算法的方式求解VRP问题,仅仅在推理速度超越目前最先进的启发式算法LKH3 和求解器OR-Tools。由于VRP 问题复杂的约束条件,目前的整体研究较少,如何选取适合的RL算法和融入传统算法的思想是未来一个重要的研究内容。
3.7 RL 求解COP 问题的方法总结
由上述综述方法可见,以RL 模型为基础的求解方法在求解速度、求解规模上超越了传统算法,甚至可以求解传统算法难以解决的问题,是近年来研究的热点方法,此方法不受人工经验的限制,可以自动发现求解问题的策略,模型一旦训练完成,可对任意类似问题进行泛化求解,摆脱了传统算法针对相同结构问题专门设计算法的弊端。随着问题规模的增大,RL 的优化效果和速度远远超越传统算法,其中基于RL 结合传统算法的求解方法、部分改进RL 模型的求解方法取代了人工设计的搜索规则,对搜索算法进行自主学习,但本质上仍然是迭代求解,速度远不如端到端的模型。基于NCO 模型的求解方法、动态输入的COP 模型的求解方法、图结构模型的求解方法等都是以端到端的形式输出解,解的收敛性和质量难以保证。由于结合PN 和GNNs,加入Attention机制,模型的性能得到提高,权衡优化效果和求解速度,可以根据实际问题的需求选择不同的优化方法。
基于RL 的COP 求解方法是一个新兴的研究领域,处于刚刚起步的阶段,到目前为止,取得的成果只能验证这个思路是可行的,并没有取得重大实质性的突破,关键在于缺少理论基础和近似比的保证。为了结合两者的优点,如采用RL 方法并加入相应的后处理操作,直接根据所给定的问题实例以端到端的方式输出解,或者将RL 算法加入到传统算法设计中,如建立RL 模型学习策略指导分支定界算法的执行。同时,可以看到一些工作中,基于RL 的方法已经能在一些实例中与传统SOTA 算法相当,从其发展历程可以看出,这个方向正随着ML 中的一些算法的蓬勃发展而快速推进,相信将来会有更多的想法被提出并融入到COP 中,它会成为传统算法的有力补充甚至会完全替代传统算法,期待RL 与CO 可以紧密结合,共同发展,推动NP 问题的求解算法与理论进展。
4 研究展望
RL 是ML 中的一个研究热点,RL 解决问题的方式和学习策略是实现智能化的一个重要途径,尤其是DRL 这种端到端的感知与决策系统的快速发展,使得这类方法广泛应用于智能交通、机器人、计算机视觉等领域。COP 问题又是实际生活中普遍存在的,传统的方法如精确算法、近似算法、启发式算法等,很难在可接受的时间内获取到问题实例的最优解。目前RL 求解COP 问题的方法与传统方法相比,是一种全新的数据驱动的求解方式,也是一个新型交叉学科。
近年来基于RL 求解COP 问题的相关工作已经大量出现,在运筹优化领域已经形成新的研究热点,如Mazyavkina 等人的综述主要梳理RL 求解COP问题的进展,提供了运筹优化和ML 的必要背景,比较了RL 算法和传统优化算法求解COP 问题的效果,说明未来可以采用RL 的方法求解COP 问题。Yang等人的综述主要针对RL 在COP 问题中的应用,以TSP 问题为例,比较了RL 算法与传统算法的差异。随着ML 的发展,阐明了计算能力对RL 中算法的影响,文献[91]阐明了DL 的方法可以迁移到COP 问题上来,可以优化TSP 问题的结果。Vesselinova 等人的综述重点梳理RL 解决图上的COP 问题的相关文献,以及总结拓展COP 问题在通讯领域中的应用。
虽然RL 理论及其应用已经取得重大进展,现有研究也展现出RL 求解COP 问题的优势,相关的应用研究仍处于探索阶段,希望各位学者可以从以下几个方面继续研究:
(1)扩大COP 问题的求解范围:针对传统算法求解大规模COP 问题速度过慢的问题,可借鉴分而治之的思想,通过子图采样、图转换、分割等技术简化搜索空间的大小,再采用热图合并、主动搜索等技术合成解,从而在RL 领域扩大求解范围。比如研究HRL,即将大规模问题分解成若干子问题来学习层次化策略,再组合子问题的策略形成全局的最优策略。同时如何有效地将其与COP 问题进行结合及解决状态分解过程的有效信息丢失问题是一个很好的研究点。
(2)求解更复杂、多类型的COP 问题:目前大多数学者的研究集中在经典的TSP、VRP 等问题上,且研究内容相对单一简单,实际上COP 问题具有动态性、多目标、多约束条件等特征,传统算法难以求解该类问题以及变体问题。未来在追求模型的精度和快速求解的要求下,基于RL 对多目标优化、多约束条件、在线动态求解等问题进行求解是一个重要的研究热点。
(3)模型上的改进:目前的研究中,许多优化模型是以端到端的形式输出解,从而解的质量较差,因此在模型改进上有很大的提升空间。同时BS、MCTS耗时长等问题影响其效率,为了提高求解速度和求解质量,未来可以进一步结合GNNs 和DRL,改进Transformer 架构中编码-解码的结构,考虑在网络结构上结合微分方程数值解的方法(用于网络参数的权重学习)进行研究,如何提高网络性能和压缩模型的大小是一个较好的研究点,进一步改善模型训练过程中收敛性差、不稳定等问题。
(4)应用范围的推广:许多运筹优化问题都满足序贯决策的性质,与高性能计算相结合,可以应用尝试快速求解各种决策问题,如何利用基于RL 求解COP 问题的方法高效解决工程实际中的动态路径规划问题、在线调度问题是一个重要的研究方向。
