基于相关向量机模型的混凝土综合性能预测
2022-02-22王鹏鹏吴哲康
张 研,王鹏鹏,吴哲康
(1.广西岩土力学与工程重点实验室,桂林 541004;2.桂林理工大学土木与建筑工程学院,桂林 541004)
0 引 言
近些年来,随着我国建筑行业的不断发展,工程中对混凝土材料的使用越发广泛,且对其综合性能的要求也越来越高[1-3]。影响混凝土性能的因素主要包括内部组成因素、外部环境因素和混凝土本身具有的特性等[4-6],混凝土综合性能易受多因素的共同作用影响,造成混凝土综合性能指标与其影响因素之间存在复杂的非线性映射关系。混凝土综合性能指标可用于指导混凝土结构的合理施工,如何快速获取该指标成为工程师和科研工作者关注的重点内容和问题。
针对上述内容和问题众,多学者对不同混凝土性能与影响因素之间的关系开展了一系列研究,如:高冠一等[7]研究了混凝土抗碳化性能与影响因素之间的关系;谢吉程等[8]对机制砂混凝土展开了研究,建立了机制砂混凝土的耐磨性与多因素之间的计算模型。尽管在试验中,能够按照规范规程来制备混凝土,但仍存在成本高、控制因素多、浪费人力、时间不足等问题。
近年来,随着人工智能的不断发展,机器学习方法逐渐应用到土木工程相关领域[9-10],特别是在利用机器学习方法建立非线性映射关系方面效果突出,如:李地红等[11]通过BP神经网络模型建立混凝土综合性能与主要影响因素之间的关系,为混凝土综合性能的预测提供了理论借鉴。但BP神经网络建立起来的模型,其自身存在过拟合、网络结构难以确定等不完善之处。因此,亟待建立高效、合理的模型,从而对混凝土的综合性能进行精准预测。
相关向量机(relevance vector machine, RVM)[12-13]是基于支持向量机发展而来,其学习的最大特点是具有稀疏性,利用该模型能极大地提高预测能力和效率[14-15]。因此,本文将参考具体实例数据,选取混凝土28 d强度、坍落扩展度及表观密度为性能评价指标,建立混凝土综合性能(28 d强度、坍落扩展度及表观密度)与其各影响因素间的非线性映射关系,进行拟合训练来达到预测混凝土28 d强度、坍落扩展度及表观密度的目的。该模型为全面、准确地解决混凝土性能指标预测、获取以及评价等方面问题提供了全新的方法和思路。
1 RVM基本原理
RVM[16-17]是基于贝叶斯原理运用到回归问题的,在数据训练中获得的稀疏化模型。RVM模型原理如下[18-20]:如果训练数据集为{xn,tn|n=0,1,2,…,N},那么令tn独立分布,建立tn的函数关系式。
tn=y(xn;ω)+ξn
(1)
(2)

(3)
式中:yc为核函数中心;δ为高斯核宽度。
设tn为相互独立分布,则似然函数表达为:
(4)
式中:t=(t1,…,tN)T;权向量ω=[ω0,ω1,…,ωN]T;Φ为核函数组成的N×(N+1)阶矩阵;σ2为高斯噪声方差。

(5)
其中,关于权重对应的参数全是独立分布的,进一步减缓了函数计算的复杂性,先验超参数αn为N+1维超参数,α=(α0,α1,…,αN),α作为权值ω的先验超参数,假定超参数α和噪声参数σ2服从Gamma先验概率分布:
(6)
P(σ2)=Gamma(c,d)
(7)
Gamma(a,b)=Γ(a)-1baαa-1e-ba
(8)

(9)
为了使上述参数没有先验知识,通常情况下规定非常小的参数数值,一般规定:a=b=c=d=0。
基于以上参数训练样本后的ω概率分布如下:
(10)
式中:∑=(σ-2ΦTΦ+A)-1,表示方差;μ=σ-2ΣΦTt,表示均值;A=diag(α0,α1,…,αN)为对角矩阵。
(11)
(12)

2 相关向量机模型
2.1 确定数据样本
混凝土的综合性能受多重因素的综合作用,通过收集文献中的试验数据得到了主要影响因素。采用RVM模型,以混凝土28 d强度、坍落扩展度及表观密度为性能评价指标,建立混凝土综合性能指标与影响因素之间的非线性映射关系。根据文献[11]及混凝土强度的直接影响因素选取压碎指标(粗骨料)、压碎指标(细骨料)、细度模数、减水剂、坍落度、7 d强度等6个主要因素作为输入数据,混凝土综合性能指标(28 d强度、坍落扩展度及表观密度)作为输出数据,混凝土综合性能样本集见表1。根据RVM回归预测模型的原理,建立基于RVM的混凝土综合性能模型,如图1所示。
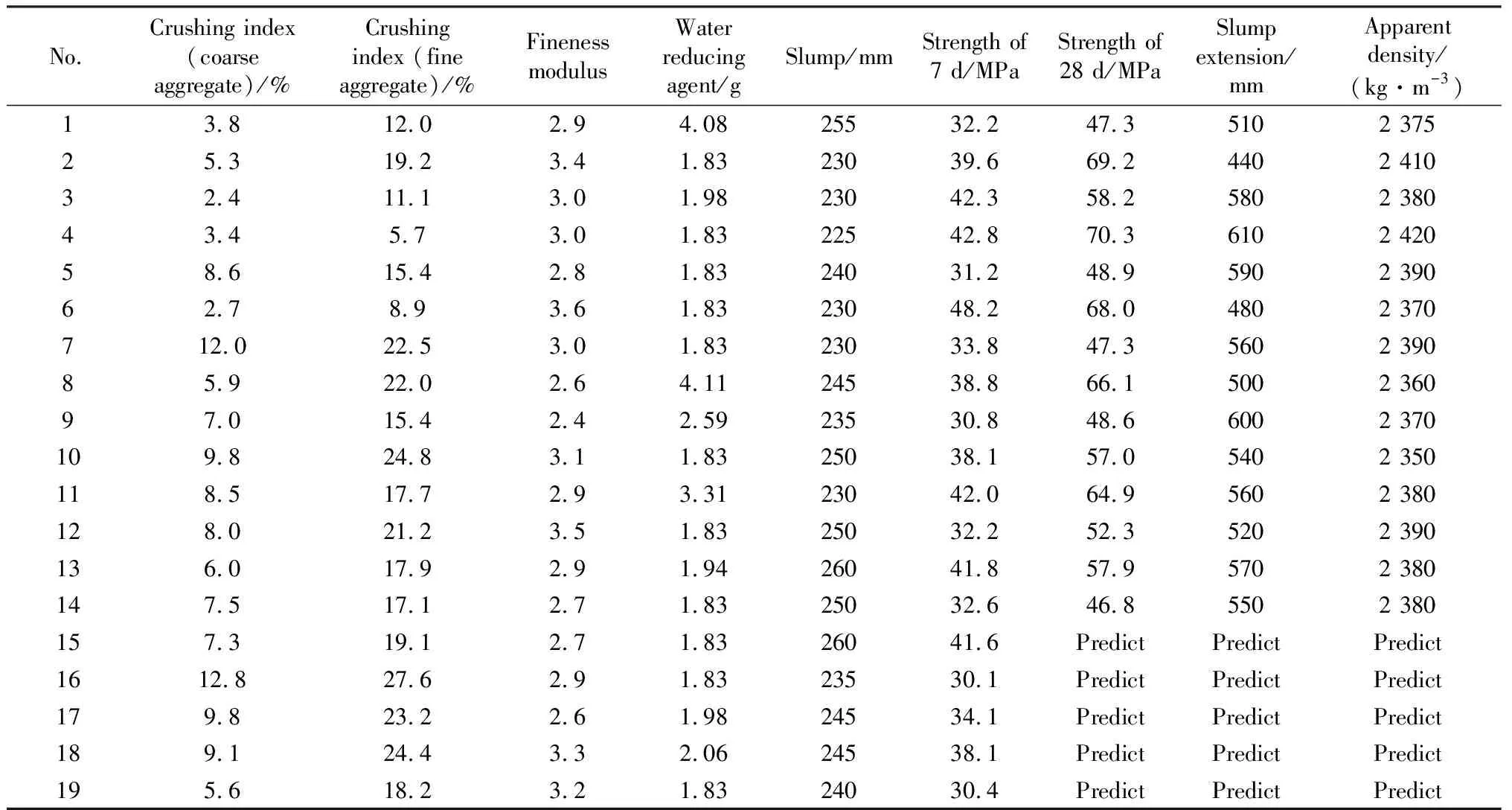
表1 混凝土综合性能样本集[11]Table 1 Sample collection of concrete comprehensive performance[11]

图1 基于RVM的混凝土综合性能模型Fig.1 Concrete comprehensive performance model based on RVM
2.2 步 骤
(1)收集混凝土试验时所得到的数据,并对数据进行分析与整理,把样本数据中的6个主要影响因素作为输入数据,把评价混凝土综合性能的3个指标(28 d强度、坍落扩展度及表观密度)作为输出数据。由于不同因素采用的单位量级差别过大会影响RVM模型预测精度,因此需要对数据进行标准化处理(见式(13))。
(13)
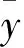
(14)
(2)以标准化处理后的输入数据和输出数据为基础建立训练集并用于拟合训练,得到模型预测参数的估计值。选取部分样本数据作为学习样本,剩余样本数据作为预测样本,对剩余样本的真实值和预测值进行对比,检测模型的预测效果。
(3)运用建立起来的RVM模型,以学习样本的预测值与实测值的误差作为精度依据,不断设置、调整模型中的超参数和迭代次数,从而找到符合该性能指标精度要求的RVM模型参数。
(4)通过调整得到符合精度要求的模型最优超参数和精度,以此RVM预测模型对预测样本进行预测分析。通过对样本实测值与相应预测值进行多个指标的对比分析(相对误差、平均相对误差等),来验证建立起来的RVM预测模型是否具有准确性和可靠性。
3 实例分析与预测结果
3.1 选取数据与建立模型
19组混凝土试验的数据如表1所示,利用上述RVM预测模型进行应用分析。在相同的数据集样本下与文献[11]中利用BP神经网络得到的预测结果进行对比分析,其中,选取前14组数据作为训练学习样本,而剩余的5组数据作为预测样本;选取压碎指标(粗骨料)、压碎指标(细骨料)、细度模数、减水剂、坍落度、7 d强度6个主要影响因素作为输入数据,混凝土的28 d强度、坍落扩展度及表观密度3个指标作为输出数据,在对这3个指标进行预测时,需根据混凝土的每一个综合性能评价指标不断设置模型中的超参数和迭代次数,从而找到符合该性能指标精度要求的RVM模型参数,建立该指标的RVM预测模型。该RVM模型主要针对小样本数据。
3.2 调整模型参数
该程序是通过调节高斯核宽度δ和迭代次数进行精准预测的,宽度参数δ、高斯核函数中心xc、可调参数在核函数的性能中起着重要的作用,高斯核函数本身较为稳定,其收敛范围宽阔,预测结果较为平稳。其中:高斯核宽度对预测结果有较大影响,若取值较小将会使方法过高估计,导致预测结果偏差较大;若取值较大将使方法低估,会对训练数据中的噪声过于敏感,使得方法的稳定性降低。迭代次数与精度作为程序收敛的两个条件,若取值太小将达不到本文所需精度要求,因此迭代次数通常取较大整数值,保证程序能够精度收敛。另外,训练样本数量多少对RVM模型参数的取值有一定的影响,其中高斯核宽度随着训练样本数量改变而变化,迭代次数取值越大其预测值越接近实际值,且训练样本数据越多,该模型所得到的预测结果越准确。
对于该样本数量下的模型,通常将高斯核宽度取2左右的数值进行调节,并由公式(3)进行检验。通过不断调节δ,得出符合混凝土28 d强度预测模型的最优高斯核宽度δ=1.7,此时预测值和实测值较为接近,通过调节迭代次数来进行加强训练,当迭代次数为100时,预测值和实测值的平均相对误差为0.050%,达到了最小值。符合混凝土坍落扩展度预测模型的最优高斯核宽度为δ=1.4,此时预测值和实测值较为接近,通过调节迭代次数来进行加强训练,当迭代次数为100时,预测值和实测值的平均相对误差为0.034%,达到了最小值。符合混凝土表观密度预测模型的最优高斯核宽度为δ=1.6,此时预测值和实测值较为接近,通过调节迭代次数来进行加强训练,当迭代次数为100时,预测值和实测值的平均相对误差为0.049%,达到了最小值。
3.3 预测结果
基于表1中的训练样本,调整选取最优超参数及迭代次数,建立RVM预测模型,对样本进行预测,结果如表2~表4所示,且表中给出了文献[11]中BP神经网络模型采用同样数据时的预测结果。结果显示:RVM模型得到的混凝土综合性能指标28 d强度、坍落扩展度及表观密度的预测值与实际值接近度更高,其中最大的相对误差绝对值为混凝土28 d强度进行预测的15号样本,为0.128%;而利用BP神经网络模型得到的混凝土28 d强度预测值的最大相对误差由18号样本得到,高达24.41%。现将这两种预测模型的各个预测样本结果进行直观对比,如图2~图4所示。

表2 BP神经网络模型和RVM模型的28 d强度预测结果及实测值比较Table 2 Comparison of 28 d strength prediction results and measured values between BP neural network model and RVM model

表3 BP神经网络模型和RVM模型的坍落扩展度预测结果及实测值比较Table 3 Comparison of slump extension prediction results and measured values between BP neural network model and RVM model

续表

表4 BP神经网络模型和RVM模型的表观密度预测结果及实测值比较Table 4 Comparison of apparent density prediction results and measured values between BP neural network model and RVM model

图2 BP神经网络模型和RVM模型的混凝土 28 d强度预测结果比较Fig.2 Comparison of prediction results of concrete 28 d strength between BP neural network model and RVM model
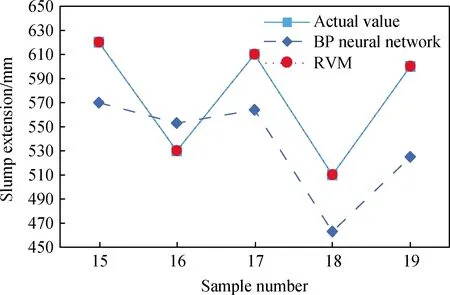
图3 BP神经网络模型和RVM模型的混凝土 坍落扩展度预测结果比较Fig.3 Comparison of prediction results of concrete slump extension between BP neural network model and RVM model

图4 BP神经网络模型和RVM模型的混凝土 表观密度预测结果比较Fig.4 Comparison of prediction results of concrete apparent density between BP neural network model and RVM model
从图2~图4可以看出:利用RVM模型得到的各预测值与实测值的接近程度明显高于BP神经网络模型得到的预测结果与实测值的接近程度。另外,观察到利用BP神经网络模型得到的混凝土28 d强度,其18及19号样本的预测值很明显已经偏离实测值;混凝土坍落扩展度,其17、18及19号样本的预测值也已偏离实测值;混凝土表观密度,其16及19号样本的预测值与实测值偏离程度较高。而利用RVM模型得到的混凝土综合性能指标的预测结果却很好。因此,相比于BP神经网络模型,RVM模型获得的预测结果精度更好、更高。现通过文献[20]中的平均相对误差(ARE)和均方差(FMSE)这两个指标来更好地对比这两种模型整体预测精度和离散情况,计算公式如下:
(15)
(16)
式中:y′i为实测值;yi为预测值;n为样本个数。
表5为RVM模型和BP神经网络模型混凝土性能指标的平均相对误差及均方差,由表中计算结果可知:RVM模型对混凝土综合性能指标预测结果的平均相对误差只有0.050%、0.034%、0.049%,均方差为0.037、0.196、1.855;而利用BP神经网络模型,其平均相对误差为10.84%、8.31%、0.95%,均方差为6.84、50.95、30.08。为了更加清晰地对比RVM模型和BP神经网络模型的平均相对误差和均方差的大小,结果如图5和图6所示。

表5 RVM模型和BP神经网络模型混凝土性能指标的平均相对误差及均方差Table 5 Average relative error and mean square error of concrete performance index of RVM model and BP neural network model

图5 RVM模型和BP神经网络模型的平均相对误差Fig.5 Average relative error of RVM model and BP neural network model

图6 RVM模型和BP神经网络模型的均方差Fig.6 Mean square error of RVM model and BP neural network model
由此看出,无论是从平均相对误差,还是均方差,RVM模型更优于BP神经网络模型。根据对比结果可得,相比于BP神经网络预测模型,本文提出的预测混凝土综合性能的RVM模型整体预测精度更高,得到的样本预测值离散性更小。
4 结 论
(1)在相同的样本数据条件下,RVM模型得到的结果比由BP神经网络模型得到的结果更好,RVM模型获得的预测值与实测值的接近程度更高;另外,RVM模型预测结果的平均相对误差及均方差均小于BP神经网络模型预测的结果,说明RVM模型具有精度高、离散度小等优点,更容易达到预期结果。
(2)利用RVM模型得到的混凝土各性能指标(28 d强度、坍落扩展度、表观密度)与实际值相比,其平均相对误差仅为0.050%、0.034%、0.049%,进一步表明RVM模型的预测值与试验实际值偏差不大,准确度高,其预测精度是可靠的。
(3)为了使RVM模型精确度更高,更有说服力,可在实际应用中收集更多试验数据,总结出更完善的非线性映射关系,降低数据的偶然性,使各影响因素之间的非映射关系更加完善,从而使建立的预测混凝土综合性能的RVM模型更具有实用性和广泛性。
