低温下泡沫混凝土的动态力学性能

吴森宝，宗 琦，王军国，汪海波，王梦想，贾 虎

(1.安徽理工大学土木建筑学院，淮南 232001；2.南阳师范学院土木建筑工程学院，南阳 200125)

0 引 言

当前，我国提倡建筑节能，绿色环保。在建筑工程中，泡沫混凝土的建筑成本比普通混凝土要便宜48%，二氧化碳排放量也相对减少48%[1]，且泡沫混凝土还具有轻质、隔热性能与隔音性能好、低弹抗震[2]等优点，这些优点使其成为建筑节能的首选材料。目前大多数研究主要针对泡沫混凝土的物理性能与静态性能，Kearsley等[3]研究了泡沫混凝土在不同孔隙率下的抗压强度，并求出了二者之间的函数关系；为了提高泡沫混凝土的力学性能，一些研究者们在泡沫混凝土中加入添加剂，如纳米改性沙[4]、粉煤灰[5]、混合纤维[6]等，此外添加剂的含量[7-8]也对泡沫混凝土的性能有一定影响;还有部分研究者关注发泡剂[9]对泡沫混凝土物理性能的影响；泡沫混凝土能与可回收废料相结合并得到应用，如废海贝[10]、碱活化矿渣[11]等，这可以降低一些废料对环境的污染。

现阶段，一些工程需要考虑泡沫混凝土的动态性能。泡沫混凝土良好的吸能特性，使其能成为隧道的隔震材料[12]；飞机的拦截系统中也采用泡沫混凝土[13]，因其吸能作用，能降低飞机降落时对起落架的伤害，以及飞机能够在降落时有效减速，不超出安全距离。因而考虑泡沫混凝土的动态性能是有必要的。在动态力学的探究中，黄海健等[14]采用φ50 mm的分离式霍普金森压杆(split Hokinson pressure bar, SHPB)装置对泡沫混凝土与普通混凝土进行冲击压缩试验，试验发现，普通混凝土的应变率效应要优于泡沫混凝土，同时通过分析泡沫混凝土的动态力学性能，改进朱-王-唐本构方程。Feng等[15]利用SHPB装置对300 kg/m3、450 kg/m3、700 kg/m3三种密度下的泡沫混凝土进行冲击压缩试验，试验发现，高密度的泡沫混凝土的应变率效应显著于低密度的泡沫混凝土，且随着密度的增加，泡沫混凝土的动态峰值应力也随之增加。Guo等[16]把泡沫混凝土作为缓冲层放置钢筋混凝土之上，对四种厚度(0 mm、200 mm、400 mm、600 mm)下的缓冲层进行落锤试验，试验发现，泡沫混凝土作为缓冲层，明显降低了落锤的冲击作用，且缓冲层厚度为400 mm时，缓冲效果好而且经济，比无缓冲层下的冲击力下降了96%。

我国冬季气温偏低，特别是青藏高原地区与西北地区，最低气温可达-30 ℃以下。泡沫混凝土的隔热性能好，这使得其作为保温墙得以应用。Ekrami等[17]利用Ansys Fluent模拟了泡沫混凝土墙在严寒地区的储热性能，丁晓燕等[18]利用泡沫混凝土设计了280 mm厚、适用于东北寒区的自保温砌块。可见，泡沫混凝土逐渐被应用于高寒地区。此外，崔玉理等[19]还通过改变水温以及环境温度养护泡沫混凝土，发现,可以根据泡沫混凝土的初凝时间选择适宜的养护温度，水温会影响泡沫混凝土的抗压强度与导热系数，且在35～40 ℃时泡沫混凝土性能最好。

然而以上对泡沫混凝土的研究仅考虑动态性能或低温下性能中的一点，将二者结合在一起考虑的研究较少。因而本文拟通过采用φ100 mm的SHPB装置在五种应变率下对低温(0 ℃及0 ℃以下的温度环境)下的泡沫混凝土试块进行冲击压缩试验。在温度效应和应变率效应中，找出在低温下抗动载设计中泡沫混凝土的优先考虑因素。

1 实 验

1.1 混凝土制备

泡沫混凝土的配合比如表1所示。

表1 泡沫混凝土配合比Table 1 Mix proportion of foamed concrete

对于泡沫混凝土这种多孔型材料，为了保证其应力均匀性，试件的长径比为0.5～0.6，本文取0.5。采用取芯机、切割机与打磨机对泡沫混凝土进行处理，得到φ100 mm×50 mm圆柱体试件，如图1所示。

图1 圆柱体泡沫混凝土试件Fig.1 Cylinder foamed concrete specimens

1.2 试验装置及试验方法

动态力学试验采用南阳师范学院的φ100 mm的SHPB装置完成，如图2所示。其中：子弹、入射杆与透射杆的直径均为100 mm，长度分别为0.8 m、4.5 m和2.5 m。本文采用的泡沫混凝土内部孔隙孔径较大，试件直径过小会导致试验数据离散性变大以及应力不均匀[20]，因此采用大直径φ100 mm压杆。由于泡沫混凝土的波阻抗低，为了采集到透射杆的透射波，透射杆采用半导体应变片，且所有压杆均采用铝杆[21]，铝杆密度为2.85×103kg/m3，弹性模量为69.35 GPa，通过计算得其波速为4 933 m/s。

图2 SHPB试验装置Fig.2 SHPB test device

根据文献[22]，本文采用二波法处理数据：

(1)

入射波、反射波与透射波所携带的能量由式(2)计算可得：

(2)

泡沫混凝土吸收能用式(3)表示：

WA=Wi-Wr-Wt

(3)

1.3 试验方案

本文拟采用5种不同的子弹速度与5种不同的温度对泡沫混凝土试件进行冲击压缩试验，即在每种温度下，分别采用5种子弹速度对泡沫混凝土进行冲击试验。子弹速度分别为3.5 m/s、4.5 m/s、5.5 m/s、6.5 m/s、7.5 m/s，温度分别为常温(10 ℃)、0 ℃、-10 ℃、-20 ℃、-30 ℃。入射波会出现明显振荡效应，需要对其整形，因而采用多孔型薄纸板作为整形器。

2 结果与讨论

2.1 应力平衡

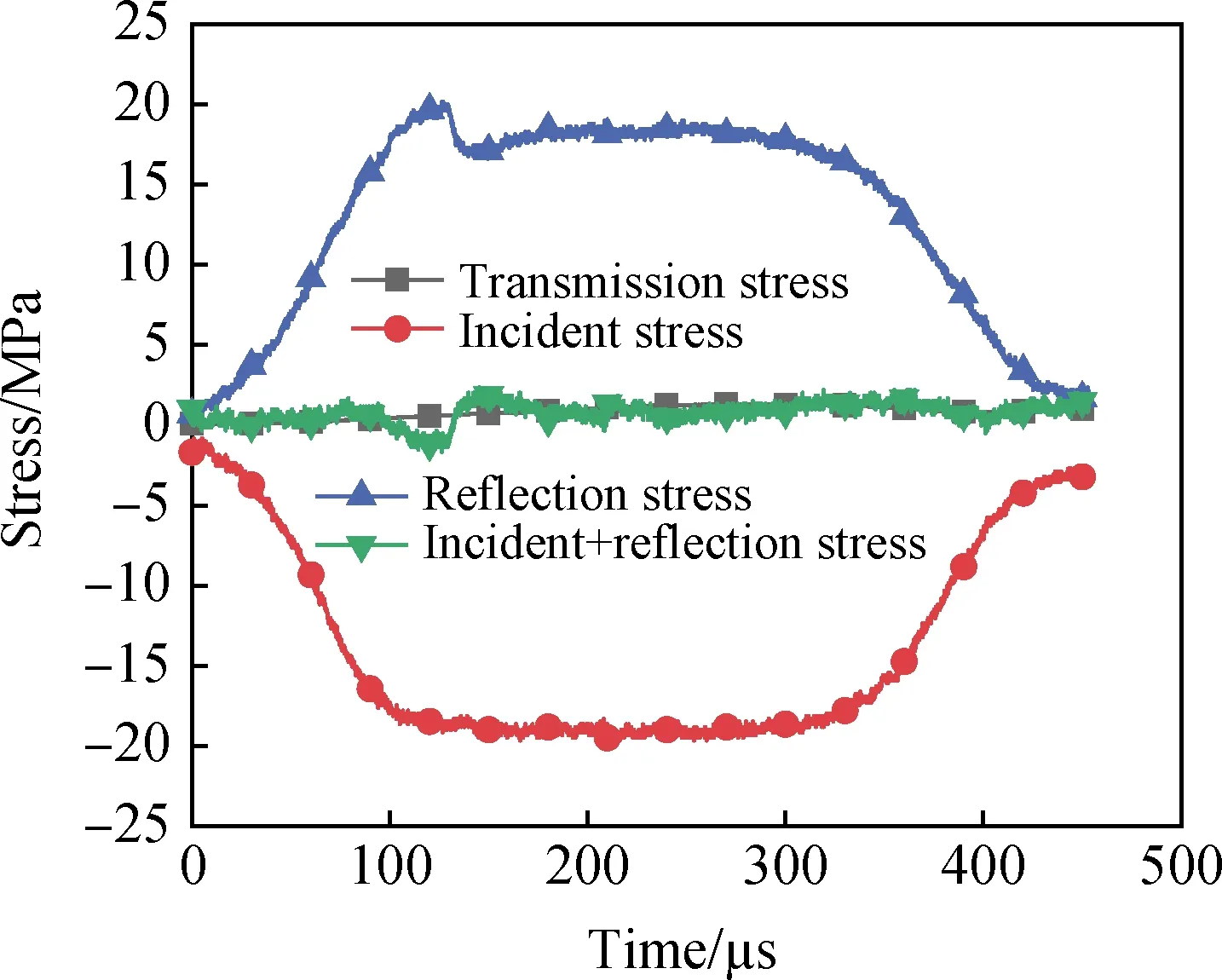
图3 泡沫混凝土应力平衡检验Fig.3 Stress balance test of foamed concrete

为了保证数据的可靠性，需检验泡沫混凝土是否达到应力平衡。图3给出了泡沫混凝土的入射应力、反射应力、透射应力和入射+反射应力。图中透射应力与入射+反射应力几乎重合在一起，说明泡沫混凝土在受冲击作用时达到了应力平衡状态。

2.2 应力应变曲线分析

通过二波法公式即可计算得到泡沫混凝土的动态应力应变数据，如图4所示。试验中有电噪声[23]的干扰，且透射杆采用半导体应变片采集电信号，噪声被放大，因而应力应变曲线有波动。

由图4(a)可知，当应变率维持在100 s-1时，泡沫混凝土在不同温度下的应力应变曲线表现出汇聚现象，汇聚趋向于温度高(常温)的应力应变曲线,其他4种应变率下的应力应变曲线也表现出汇聚现象。而不同应变率下的应力应变曲线有所不同，如图4(b)所示。

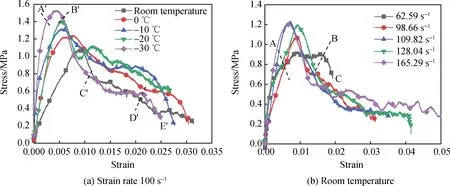
图4 泡沫混凝土的应力应变曲线Fig.4 Stress-strain curves of foamed concrete

以62.59 s-1为分界，当应变率小于62.59 s-1时，泡沫混凝土的动态应力应变曲线主要分为3个阶段：

(1)线弹性阶段，即0A段，加载初期，应力随应变大致呈线性增长；

(2)屈服阶段，即AB段，泡沫混凝土依靠其孔壁骨架继续承受冲击荷载,形成应力平台，此时孔壁已开始发生破坏；

(3)破坏阶段，即BC段，泡沫混凝土完全破坏，应力随应变的增长而降低。

当应变率大于62.59 s-1时，泡沫混凝土的应力应变曲线主要分为5个阶段，如图4(b)所示：

(1)线弹性阶段，即0A′段，此时，泡沫混凝土依靠弹性变形承担冲击荷载;

(2)屈服阶段，即A′B′段，应力集中于泡沫混凝土内部的孔壁上，应力与应变呈现非线性关系;

(3)局部失稳，即B′C′段，当应力达到峰值后，泡沫混凝土的微裂纹扩展，应力突然下降至平台段;

(4)应力平台，即C′D′段，泡沫混凝土具有许多孔隙，在受到冲击作用后，内部孔结构破坏后所产生的泡沫混凝土颗粒填充未损坏的孔结构，这能消除局部失稳并产生压缩变形;

(5)破坏阶段，即D′E′段，泡沫混凝土完全破坏，应力随着应变的增长而降低。

应变率大小影响应力应变曲线特征的主要原因是：在较低应变率下，泡沫混凝土的破坏形式主要以均匀压实破坏为主；随着应变率的增加，泡沫混凝土的破坏形式由均匀压实破坏转向逐层塌落破坏。

2.3 应变率效应对泡沫混凝土动态性能的影响

图5给出了不同温度下泡沫混凝土的峰值应力与应变率之间的关系。从图中可以看出，泡沫混凝土在虚线左侧表现出明显的应变率效应，即峰值应力随应变率的增大而增大。超过虚线后，应变率效应则表现得不显著。这与黄宝峰等[24]的轻质高强混凝土冲击试验相似，当子弹处于高速度状态时，混凝土的应变率效应不显著。从应变率效应显著阶段的起点到终点，泡沫混凝土在常温、0 ℃、-10 ℃、-20 ℃、-30 ℃的动态抗压强度分别提高了34%、15%、25%、35%、33%。

从图5中还可以看出，随着温度的降低，泡沫混凝土应变率效应显著区域与不显著区域的分界点所对应的应变率逐渐变大，即分界点所对应的应变率从109.82 s-1增长到123.75 s-1。这说明随着温度的降低，泡沫混凝土的应变率效应逐渐变好。其主要原因是泡沫混凝土孔隙内含有孔溶液，当泡沫混凝土处于低温状态时，孔溶液形成冰，而冰在60～1 400 s-1具有较为明显的应变率效应[25]，当温度降低时，冰与泡沫混凝土共同承受荷载，因而泡沫混凝土的应变率效应随着温度的降低而提高。

图6表示不同应变率下泡沫混凝土的吸收能与应变率之间的关系。可以看出：吸收能一开始表现出显著的应变率效应，即吸收能随着应变率的增加而增加；但当吸收能达到“阈值”时，便不再随应变率增加而增加。其主要原因是随着应变率的增加，入射能也随之增加，根据能量守恒，泡沫混凝土需吸收能量平衡入射能，但泡沫混凝土吸收能量的能力有限，所以当入射能超过能量“边界”且继续增加时，吸收能便不再变化。同峰值应力的应变率效应，虚线左侧为吸收能的应变率效应显著阶段，右侧为应变率效应不明显阶段。此外，阶段分界点的应变率随着温度降低也在增大，说明吸收能的应变率效应随着温度的降低而提高。在常温、0～-30 ℃ 5个温度状态下，泡沫混凝土从应变率显著阶段的起点到终点，其吸收能分别提高了64%、123%、137%、170%、133%。

图5 峰值应力与应变率之间的关系Fig.5 Relationship between peak stress and strain rate

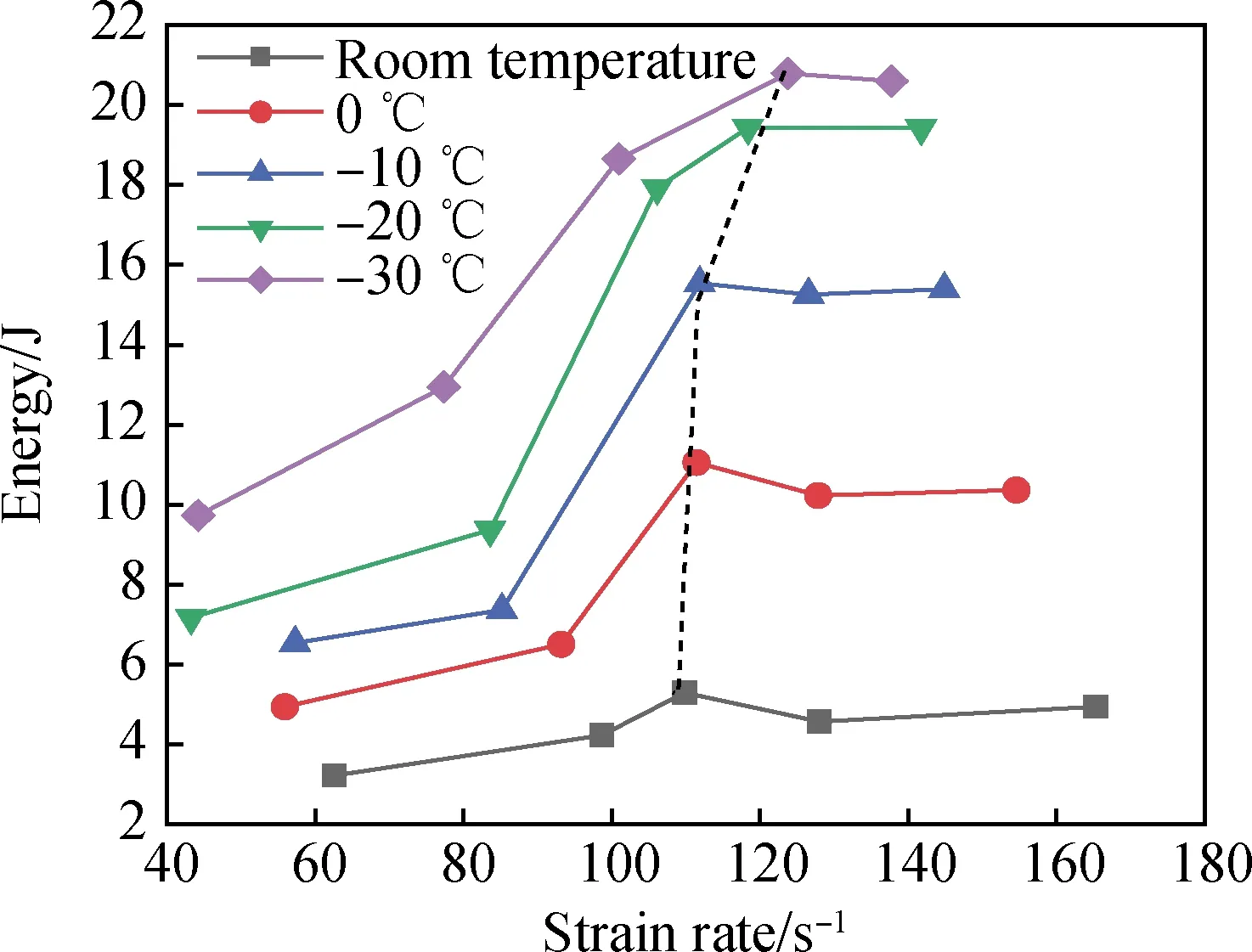
图6 吸收能与应变率之间的关系Fig.6 Relationship between absorption energy and strain rate

2.4 温度效应对泡沫混凝土动态性能的影响

图7给出了不同温度下泡沫混凝土的动态峰值应力。由图可知，泡沫混凝土的峰值应力随着温度的降低而提高。从常温下降到-30 ℃，5种子弹速度下的峰值应力分别提高了56%、44%、42%、59%、56%。其主要原因：(1)在低温处理泡沫混凝土时，周围空气中的水分遇冷形成冰层并与泡沫混凝土紧密贴合，对其起到了加固的作用，因而其峰值应力得以提高；(2)泡沫混凝土为多孔隙材料，孔隙含有孔溶液，遇冷形成冰，同时孔隙内也有水汽遇冷形成冰层与孔壁紧密贴合，使得孔隙不易发生破坏；(3)泡沫混凝土为亲水材料，随着温度降低，泡沫混凝土与冰的黏接强度也随之提高，而在同一条件下，冰与泡沫混凝土的结合强度要大于冰的强度；(4)泡沫混凝土内含有β-H2O(易蒸发水)，随着温度的降低，β-H2O的含量减少，而β-H2O的消失能提高低温下泡沫混凝土的强度。此外，由于温度的降低，冰的动态抗压强度也随之增强[26]。正是由于冰的这一特性，泡沫混凝土的动态抗压强度随温度的降低而提高。

为了进一步探究温度与泡沫混凝土动态峰值应力的关系，对图7中的数据点进行线性拟合。各个子弹速度下的拟合曲线的R2分别为0.971、0.979、0.944、0.967、0.956，这说明泡沫混凝土的动态峰值应力与温度呈线性关系。

不同应变率下泡沫混凝土的峰值应变与温度之间的关系如图8所示。从图中可以看出，泡沫混凝土的峰值应变随着温度的降低而降低，说明其延性随着温度的降低逐渐变差。随着温度的降低，冰的动态峰值应变也降低，而泡沫混凝土内部在低温状态下会形成冰，所以其峰值应变也随温度的降低而降低。对图中数据进行线性拟合，发现峰值应变与温度也呈线性关系。但拟合直线的斜率“k”都很小，说明泡沫混凝土的峰值应变随温度降低的降低幅度都很小。

图7 动态峰值应力与温度之间的关系Fig.7 Relationship between dynamic peak stress and temperature

图8 动态峰值应变与温度之间的关系Fig.8 Relationship between dynamic peak strain and temperature

图9 吸收能与温度之间关系Fig.9 Relationship between absorption energy and temperature

在不同应变率下泡沫混凝土的吸收能与温度之间的关系如图9所示。从图中可以看出，泡沫混凝土吸收能的温度效应都很明显，且其吸收能随温度的降低而提高。这与Qiao等[27]所得的结果一致，说明低温使泡沫混凝土吸收更多的能量。其原因是，当温度降低时，泡沫混凝土内部与外部都会形成冰，与泡沫混凝土共同承受冲击压力。而冰的破坏需要吸收比原来更多的能量，随着温度的降低，冰的强度也随之提升，使其发生破坏需要吸收更多的能量，所以泡沫混凝土的吸收能不断提高。还可以看出：当子弹速度在3.5 m/s、4.5 m/s时，温度与吸收能大致呈线性关系；而当子弹速度增大到5.5 m/s以后，吸收能随温度的降低先大幅度增长，到-20 ℃后，吸收能增长幅度开始变小。

2.5 应变率效应与温度效应对比

为了更好地对比应变率效应与温度效应，截取泡沫混凝土应变率效应显著阶段与温度效应进行对比。由图5可知，在常温、0 ℃、-10 ℃、-20 ℃和-30 ℃下，泡沫混凝土应变率效应显著的区间分别为62.59～109.82 s-1、52.88～111.42 s-1、57.30～111.87 s-1、43.27～118.41 s-1和44.20～123.75 s-1。

本文引入η1、φ1、ψ1分别表示峰值抗压强度、峰值应变、吸收能的温度增长因子，η2、φ2、ψ2分别表示峰值抗压强度、峰值应变、吸收能的应变率增长因子[27]。如式(4)表示：

(4)

式中：ηi,1、φi,1、ψi,1分别代表子弹速度i下泡沫混凝土的峰值应力、峰值应变、吸收能的温度增长因子；σi,-30、εi,-30、Wi，-30分别代表子弹速度i、-30 ℃时泡沫混凝土的峰值应力、峰值应变、吸收能；σi，10、εi，10、Wi,10分别代表子弹速度i、10 ℃时泡沫混凝土的峰值应力、峰值应变、吸收能；i分别为3.5 m/s、4.5 m/s、5.5 m/s、6.5 m/s、7.5 m/s；ηj,2、φj,2、ψj,2分别代表温度j下，泡沫混凝土峰值应力、峰值应变、吸收能的应变率增长因子；σj,T、εj,T、Wj,T分别代表温度j下应变率效应作用阶段泡沫混凝土的最大应变率对应的峰值应力、峰值应变、吸收能；σj,L、εj,L、Wj,L分别代表温度j下应变率效应作用阶段泡沫混凝土的最小应变率对应的峰值应力、峰值应变、吸收能；j分别为-30 ℃、-20 ℃、-10 ℃、0 ℃、10 ℃。

图10为峰值抗压强度、峰值应变、吸收能的温度和应变率增长因子与应变率、温度的关系。从图10(a)中可以看出，η1、η2都大于1，说明温度的降低与应变率的提高都是使泡沫混凝土的动态抗压强度呈正增长的。η1随应变率的增加变化不明显，且η2随温度的增加变化也不显著。从图中还可看出η1>η2，说明温度效应对泡沫混凝土的影响要强于应变率效应。另外，当达到一定应变率时，泡沫混凝土的应变率效应会变得不显著，而不论何种温度下温度效应都很明显，这也说明温度效应对峰值抗压强度影响强于应变率效应。

从图10(b)可看出，φ1<1、φ2>1，说明温度效应和应变率效应对应变的影响相反，即温度的降低使应变负增长，应变率效应使应变正增长。随着温度的降低，φ2大致呈增加的趋势，说明随着温度的降低，温度使应变的应变率效应越来越显著，而随着应变率的增加，φ1越来越趋向于1，说明应变的温度效应在逐渐减弱。φ2与1的距离大于φ1与1的距离，说明应变率效应对泡沫混凝土应变的影响更大。

图10(c)中的ψ1、ψ2均大于1，说明温度效应与应变率效应都使吸收能增加。在3.5～6.5 m/s之间，随着应变率的增加，ψ1也在增加，说明在此区间内吸收能的温度效应随着应变率的提高而提高；在10～-20 ℃之间，ψ2随着温度的降低在提高，即在此区间内温度越低，应变率效应越好。此外，还可观察出ψ1>ψ2，得出两种效应之中，温度效应对吸收能的影响最大。

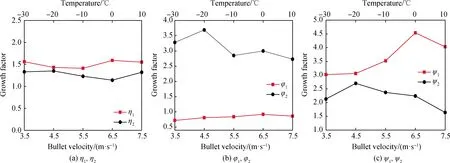
图10 峰值抗压强度、峰值应变、吸收能的温度和应变率增长因子与应变率、温度的关系Fig.10 Relationship between temperature and strain rate growth factors of peak compressive strength, peak strain, absorption energy, and strain rate and temperature

综上所述，低温状态下研究泡沫混凝土时，温度效应对其动态抗压强度与吸收能影响更明显，而应变率效应对其峰值应变影响更显著。

2.6 破碎形态

图11～图15给出了常温与低温状态下泡沫混凝土的最终破坏形态。从图中可以看到，泡沫混凝土的部分孔隙被其孔壁破碎后形成的粉状泡沫混凝土填充，说明其在受到压杆撞击时被压实，形成了图4(a)中应力应变曲线中的应力平台。随着子弹速度的增大，泡沫混凝土更倾向于逐层破坏，因而在应力应变曲线中的应力平台会更长。泡沫混凝土的破碎块度随着子弹速度的增大而变小，且粉状的泡沫混凝土也在逐渐增多，但超过一定阈值后，破坏形态差异并不大。其主要原因是泡沫混凝土完成破坏过程需要吸收能量，吸收能达到相应应变率后便不再增加，因而超过一定应变率后，破坏形态便没发生太大变化，如图6所示。

为探究破碎形态与温度之间的关系，比较了低应变率下的破碎形态。随着温度的降低，泡沫混凝土的破坏块度逐渐变大。选取常温状态与-30 ℃下的破碎样本，发现常温状态下受冲击后粉末状泡沫混凝土明显多于后者，这说明低温下泡沫混凝土的整体性优于常温状态下，且随着温度的降低，泡沫混凝土的抗冲击性能逐渐变强。尽管泡沫混凝土的吸收能随温度的降低而增大(见图9)，但泡沫混凝土的整体性却越好。这是因为泡沫混凝土在低温状态内部所形成的冰使水泥颗粒能更好地连接在一起，且受冲击时，其内部的冰能替泡沫混凝土抵消部分冲击能。

图11 常温状态下泡沫混凝土的最终破碎形态Fig.11 Final crushing form of foamed concrete at normal temperature

图12 0 ℃状态下泡沫混凝土的最终破碎形态Fig.12 Final crushing form of foamed concrete at 0 ℃

图13 -10 ℃状态下泡沫混凝土的最终破碎形态Fig.13 Final crushing form of foamed concrete at -10 ℃

图14 -20 ℃状态下泡沫混凝土的最终破坏形态Fig.14 Final failure form of foamed concrete at -20 ℃

图15 -30 ℃状态下泡沫混凝土的最终破坏形态Fig.15 Final failure form of foamed concrete at -30 ℃

3 结 论

(1)当应变率小于62.59 s-1时，泡沫混凝土的应力应变曲线分为3个阶段：线弹性阶段、屈服阶段、破坏阶段；而应变率大于62.59 s-1时，应力应变曲线分为线弹性阶段、屈服阶段、局部失稳、应力平台、破坏阶段5个阶段。在同一应变率作用下，不同温度下的应力应变曲线具有汇聚现象，汇聚趋向于温度高(常温)的曲线。

(2)泡沫混凝土的动态抗压强度，吸收能在常温、0 ℃、-10 ℃、-20 ℃及-30 ℃的应变率效应显著阶段分别在62.5～109.82 s-1、52.88～111.42 s-1、57.30～111.87 s-1、43.27～118.41 s-1及44.20～123.75 s-1。当应变率超过分界点，应变率效应便不再显著。应变率效应分界点的应变率数值随着温度的降低而增加，说明温度的降低提高了泡沫混凝土的应变率效应。

(3)泡沫混凝土的峰值抗压强度、吸收能、峰值应变具有温度效应，峰值抗压强度与吸收能随着温度的降低而提高，且峰值抗压强度与温度呈线性关系，但是峰值应变随温度的降低而变小。破碎块度随温度的降低而变大。

(4)在低温环境下，影响泡沫混凝土动态抗压强度和吸收能的首要因素是温度效应，影响泡沫混凝土动态峰值应变的首要因素是应变率效应。